Effect of kinetic energy on stress behavior of coated glass plates

1. Introduction

Films that can withstand external wind and impact are coated on glass plates mainly to absorb the impact by reducing the stresses on the actual glass plates. When a coated glass plate is impacted by an external object, the glass plate experiences stress and can get damaged. Coated glass plates, unlike homogeneous materials, can reduce the damage due to flight debris by capturing fragments on the film layers. Therefore, the coated film can greatly reduce the risk of injury by acting as a barrier to broken glass, preventing it from penetrating inside, and the overall weight of the coated glass can be reduced without reducing the overall thickness.

The stress induced by the contact between two objects is referred to as contact stress. Hertz [1] presented the theory of contact to calculate the size, deformation, and stress of contact surfaces with simple shapes, such as spheres and cylinders, but it is of great importance to help recognize contact behavior. According to the Hertz theory, there is an area in which the contact pressure inside the contact surface decreases to zero at the point inside the object, not at the center of the contact surface. Recently, many studies investigated the impact behavior of laminated and coated glass plate systems [2]-[4].

The classic Hertz contact law cannot explain the pressure response of thin-film-coated glass plates to compression owing to the complexity of the deformation and stress fields of the coated glass. Recently, Kurapati [5] proposed the generalized power law (load-deflection curve), which can be applied when the film thickness and coefficient change in the layered system, and verified it using ABAQUS.

In this study, an effective impact finite element approach was used in conjunction with the high-order shear deformation theory of Reddy [6] and generalized power law to study the micro behavior of coated glass plates subjected to low-velocity impact load due to changes in the kinetic energy. Finally, we will study the micro behavior such as stress etc. by changes in the four kinetic energies, namely the impact velocity V=5, 10, 20, and 30 m/s.

2. Fundamental Theory

We investigate a geometry and a quarter model of the target consisting of two layers with film thickness h_f of 0.2 mm and a glass thickness h of 4 mm under a drop weight impact of radius R of 6.35 mm at the center with initial velocity V₀. The stress behavior between the target and impactor is predicted by calculating the displacement components of a point at a distance of z from the reference plane according to Reddy’s high-order shear deformation theory [6] as follows:

where (u₀, v₀, w₀, φ_x, φ_y) are unknown functions to be determined. The equivalent material properties of the coated glass plate are used to calculate the contact stiffness using Kurapati’s generalized power law [5] as

where F, δ, p, and CE_s are the contact force, indentation, power, and contact stiffness, respectively.

According to Equation (2), the contact force–deflection response for the indentation of the coated film/glass plate follows a general power law relation. To obtain the numerical analysis results of the stress behavior of the coated glass plate, we applied a generalized power law than considered the Hertzian contact law, Newton's second law, and the Newmark's integration scheme for solving the dynamic equations. Because glass is brittle, the loading and unloading processes are treated as elastic. The glass plates are assumed to be impacted at the center by a steel ball impactor.

The details of the simulation processes utilized in this study can be found in References [2]-[4].

3. Results and Discussion

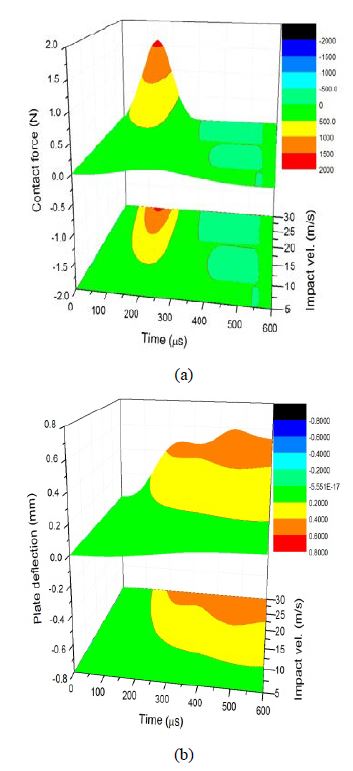
Figure 1 (a) and (b) shows the 3D dynamic behaviors of the contact force and deflection, respectively, according to the changes in the impact velocity. From the figure, it can be seen that a higher impact velocity led to a greater maximum contact force and deformation of the plate and a shorter contact time. Furthermore, the impact response to all variables except the impact velocity was inversely proportional to the maximum contact force, as found in References [2]-[4]. Therefore, if there are other parametric changes without changes in the impact velocity, the increase in the maximum contact force will result in a reduction in the contact duration and maximum deflection.

Figure 1:

3D histories of (a) contact force and (b) deflection according to changes in impact velocity

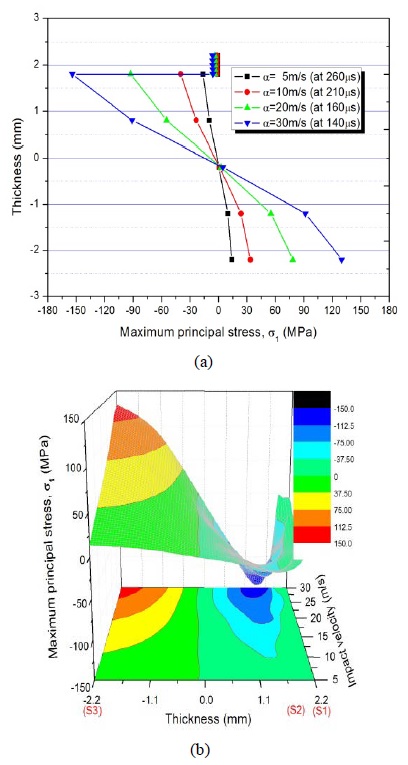
Figure 2 (a), (b), and (c) shows the stress histories of σ_x, σ_y, and σ_xy on the film–glass interface (the surface on the glass plate), referred to as surface S2, respectively, according to the changes in the impact velocity. From the figure, it can be seen that a larger impact velocity led to greater stresses σ_x, σ_y, and σ_xy on S2. Figure 3 (a), (b), and (c) shows the 3D shapes and contours of principal stress σ₁ at an impact velocity of 10, 20, and 30 m/s, respectively. From the figure, it can be seen that as the impact velocity increased, the principal stress rapidly increased at the impact point and caused a large wave in the coating glass plate. Figure 4 shows 2D and 3D distributions of the stress σ₁ along the thickness according to the changes in impact velocity. It can be seen that unlike most homogeneous materials, in which the maximum stress σ₁ is on the surface right underneath the indenter, the coated glass plate experienced the maximum stress σ₁ on the interface between film and glass. All stress components obtained by first-order shear deformation theory vary linearly through the thickness [7], whereas the stress components obtained by higher-order theory vary nonlinearity. As can be seen from Figure 4 (a), a discontinuance was obtained by higher-order theory due to the significant difference in the material properties of the film and glass. Finally, the interface S2 was more prone to failure risk than the other layer owing to the difference in the maximum stress σ₁ of the two layers.

Figure 2:

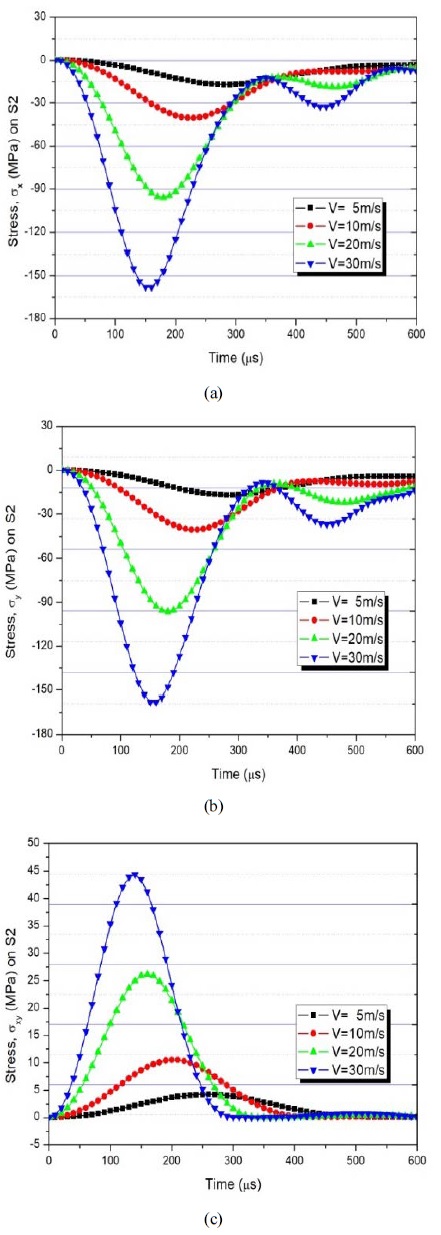
Evolution on (a) σx, (b) σy, and (c) σxy on the film–glass interface (S2) with different impact velocity

Figure 3:

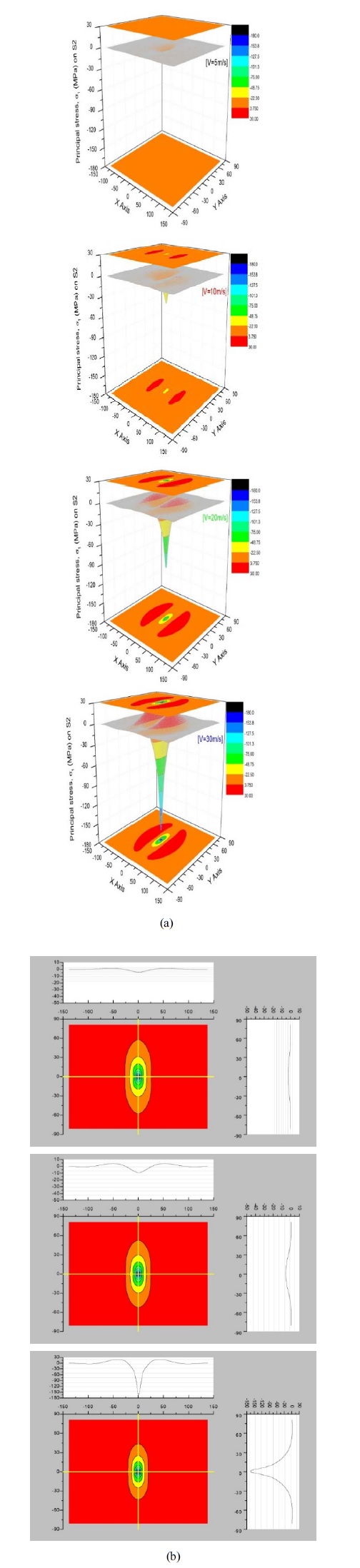
(a) 3D shapes and (b) contours of principal stress σ1 on the film–glass interface (S2) at different impact velocities

Figure 4:

(a) 2D and (b) 3D variations in stress σ1 along the thickness at different impact velocities

4. Conclusions

The stress behavior of glass plates coated with thin films at different impact velocities (5, 10, 20 and 30 m/s) was investigated using a powerful impact finite element approach in conjunction with the Reddy’s higher-order shear deformation theory and a generalized power law. The results indicate that as the impact velocity increases, the contact force and deformation at the point of contact increase significantly. Unlike most homogenous materials, which experience the maximum principal stress σ₁ on the surface right underneath the indenter, the coated glass plate experienced the maximum principal stress σ₁ on the interface between film and glass. This indicates that the film–glass interface is more prone to failure than the other layer. The simulation approach established in this study allows the quantitative evaluation of the impact behavior of coated glass plates according to the impact energy.

Acknowledgments

This work was supported by the research invigoration program of 2020 Gyeongnam National University of Science and Technology.

References

• W. Goldsmith, Impact. The Theory and Physical Behaviour of Colliding Solids, Edward Arnold Ltd., 1960.
• H. D. Kang and K. C. Ahn, “A study on the dynamic behaviour of the coating tempered glass plate under impact,” International Journal of Mechanical and Production Engineering Research and Development (IJMPERD), vol. 8, no. 6, pp. 193-200, 2018. [https://doi.org/10.24247/ijmperddec201823]
• K. C. Ahn, “A comparative study on the impact behaviour of the coating glass plates by FSDT and HSDT,” International Journal of Mechanical and Production Engineering Research and Development (IJMPERD), vol. 8. no. 6, pp. 479-486, 2018. [https://doi.org/10.24247/ijmperddec201851]
• K. C. Ahn, “Impact response of the film mechanical properties of the coated glass plate,” International Journal of Mechanical and Production Engineering Research and Development (IJMPERD), vol. 9, no. 2, pp. 499-506, 2019. [https://doi.org/10.24247/ijmperdapr201948]
• S. N. V. R. K. Kurapati, Y. C. Lu, and F. Yang, “Indentation load-displacement relations for the spherical indentation of elastic film/substrate structures,” Computers, Materials & Continua (CMC), vol. 20, no. 10, pp. 1-17, 2010.
• J. N. Reddy, “A simple higher-order theory for laminated composite plates,” Journal of Applied Mechanics (ASME), vol. 51, no. 4, pp. 745-752, 1984. [https://doi.org/10.1115/1.3167719]
• H. D. Kang and K. C. Ahn, “A study on the dynamic behavior of the coating tempered glass plate under impact,” International Journal of Mechanical Production and Engineering Research and Development, (IJMPERD), vol. 16, no. 6, pp. 193-200, 2018. [https://doi.org/10.24247/ijmperddec201823]