Effect of kinetic energy on dynamic behavior of Nanoclay/Epoxy nanocomposites

1. Introduction

Composites are used in many structures, such as automobiles and buildings, owing to their mechanical properties, such as light weight and abrasion resistance. Because the addition of a few nanoclays can significantly improve the mechanical properties of the original composites, research and the industry have shown interest in using nanoclays for reinforcing polymer-based composites. Nevertheless, several studies on the impact response of nanocomposites have been conducted experimentally to evaluate the impact of external objects on nanocomposites. Wuite et al. [1] analyzed nanocomposites using the classical composite theory but did not apply the law of contact. Meybodi et al. [2] applied the Euler–Bernoulli theory to investigate the impact response of nanocomposites and examined the effects on the impact response of various beam variables, such as nanoclay content, initial velocity, stacking sequence, and geometric parameters. Reddy et al. [3] conducted an experimental study on the effects of nanoclay and incident energy on the impact resistance of laminates under impact. However, there is a need to introduce a higher order theory to improve the degree of interpretation. The third-order theory [4] is nonlinear, does not require shear correction used in the linear theory [5], and can be used to predict more accurate stress conditions.

Therefore, a simulation of the dynamic behavior of nanocomposites based on the kinetic energy was performed in this study using a third-order theory. Combinations of four kinetic energies of 0.051, 0.204, 0.817, and 1.84 J, with corresponding impact velocities of 5, 10, 20, and 30 m/s, respectively, were considered. Finally, the dynamic behaviors of contact force, deflection, absorbed energy and coefficient of restitution (COR), owing to variations in kinetic energy, were investigated.

2. Theoretical Background

The nanoclay/epoxy nanocomposite consisted of 20 layers (a layer: 0.25 mm) laid at [0/45/0/-45/0]_2S, and the nanoclay content 5 wt.% NC. The kinetic energies were 0.051, 0.204, 0.817, and 1.84 J, with corresponding impact velocities of 5, 10, 20, and 30 m/s, respectively. The formulations were based on a third-order theory [3], and the detailed processes are described in References [6][7].

For the changes in the dynamic behavior of the nanocomposites owing to variations in the impact velocity, combinations of the four kinetic energies of 0.051, 0.204, 0.817, and 1.84 J, and corresponding impact velocities of 5, 10, 20, and 30 m/s were considered. The nanocomposites were composed of 20 layers at [0/45/0/-45/0]2S with a nanoclay content of 5 wt.% NC, and Young’s modulus of Chan et al. [8] was adopted. The mechanical properties were modified using the modified rule of mixture (MROM) [9] to obtain transverse properties of the nanocomposite that are more accurate than those of the rule of mixture (ROM) (Table 1). The MROM properties are expressed as follows:

Table 1:

Young's modulus of nanoclay/epoxy at [0/45/0/-45/0]2S containing 5 wt.% NC

where E, G, and V are the elastic modulus, shear modulus, and volume fraction, respectively. The subscripts f and eq,m indicate the fiber and equivalent properties of the nanocomposite, respectively.

3. Results and Discussion

Figure 1 shows the relationships of the contact force and –deflection of nanocomposites with time for different impact velocities. As the kinetic energy increased, the maximum contact force and maximum plate deflection increased, and the contact duration decreased (Figure 1).

Figure 1:

Variations in (a) contact force and (b) deflection with time for different impact velocities

Generally, for variables of geometry change, the contact force and plate deflection tended to be opposite for most dynamic responses, but for the kinetic energy variables, the two relationships tended to be similar. In other words, as the kinetic energy increased, the contact force and plate deflection increased, and vice versa. Figure 2 depicts the contact force–indentation relationship for different impact velocities. All work done by an impactor on the nanocomposite plates during the loading process was kinetic energy. We can see that the slope remained constant, regardless of the impact velocity, but the magnitude depended on the impact velocity. This showed that the higher the impact, the more likely that the nanocomposites were exposed to damage.

Figure 2:

Relationship between contact force and indentation for different impact velocities

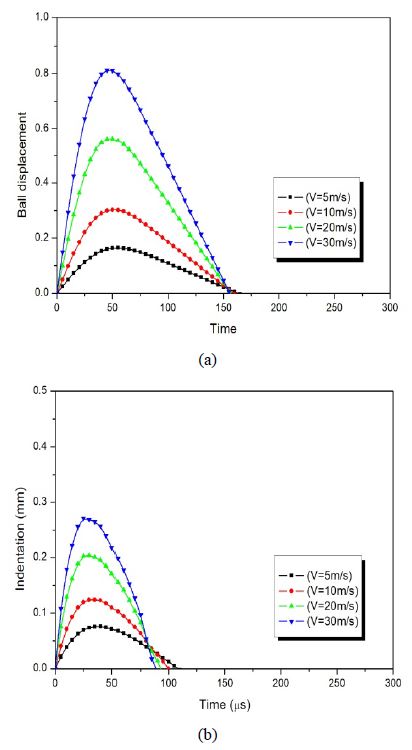
Figure 3 shows the contact force–deflection and contact force–ball displacement relationships. Figure 4 shows the variations in ball displacement and indentation with time for different impact velocities. It was found that there was no maximum contact force at the time of the maximum plate deflection and maximum ball displacement, which indicated a typical wave-controlled impact [10][11]. The higher the impact velocity, the higher the contact force, plate deflection, and ball displacement.

Figure 3:

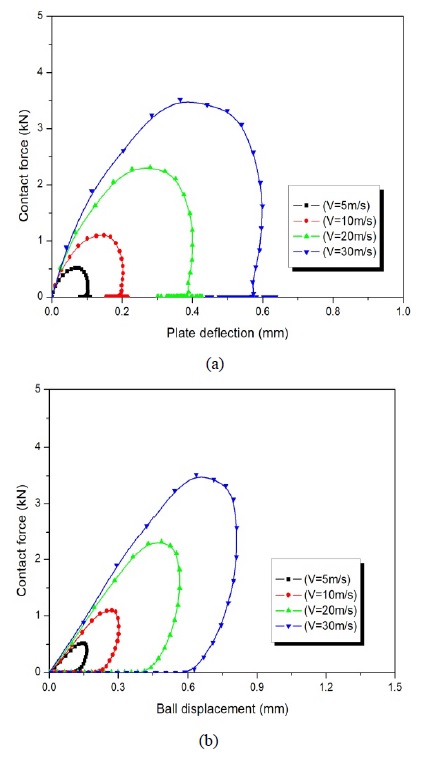
(a) Contact force–plate deflection and (b) contact force–ball displacement relationships for different impact velocities

Figure 4:

Variations in (a) ball displacement and (b) indentation with time for different impact velocities

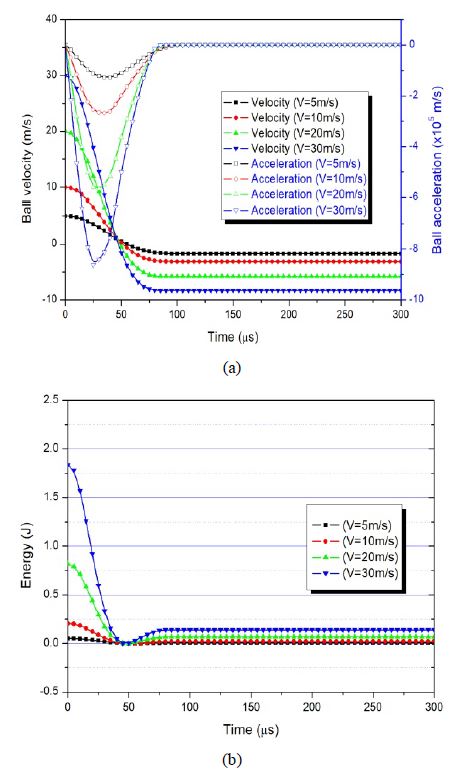
Figure 5 depicts the variations in the ball velocity and kinetic energy with time for different impact velocities. At the time was zero, the impactor provided the initial velocity and initial energy when it hit the nanocomposites. The energy difference (initial rebound) was the absorbed energy of the nanocomposites.

Figure 5:

Variations in (a) ball velocity and (b) energy with time for different impact velocities

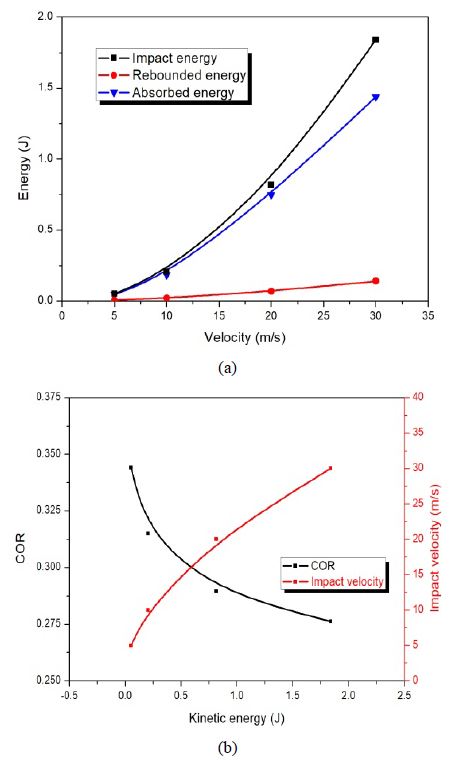
Figure 6 depicts the energy–impact velocity and COR–impact velocity–kinetic energy relationships. It was found that the higher the impact velocity, the higher the rebound and absorbed energy, but the lower the COR.

Figure 6:

(a) Energy–impact velocity and (b) COR–impact velocity–kinetic energy relationships

4. Conclusions

A study on the kinetic energy of the dynamic behavior of nanoclay/epoxy nanocomposites subjected to external impact was conducted using a third-order plate theory based on a contact law. Young's modulus was modified using the MROM to determine transverse properties of the nanocomposite that are more accurate than ROM properties. Combinations for four kinetic energies of 0.051, 0.204, 0.817, and 1.84 J, with corresponding impact velocities of 5, 10, 20, and 30 m/s, respectively, were considered. The nanocomposites were composed of 20 layers at [0/45/0/-45/0]_2S with a nanoclay content of 5 wt.% NC. It was found that an increase in the impact velocity or kinetic energy increased the maximum contact force and plate deflection but decreased the contact duration. The maximum contact force and deflection of the nanocomposites increased, and the contact duration decreased. This behavior was different from the tendency of contact forces and plate deflections of the impact characteristics when other geometric variables, other than the impact velocity, changed. Moreover, as the kinetic energy increased, the contact force, plate deflection, rebound energy, and absorbed energy increased, whereas the COR decreased. These results are critical factors that should be considered in the design and manufacture of impact-prone composite materials.

Acknowledgments

This work was supported by Gyeongnam National University of Science and Technology Grant 2020.

References

• J. Wuite and S. Adali, “Deflection and stress behaviour of nanocomposite reinforced beams using a multiscale analysis,” Composite Structures, vol. 71, no. 3-4, pp. 388-396, 2005. [https://doi.org/10.1016/j.compstruct.2005.09.011]
• M. H. Meybodi, S. Saber-Samandari, M. Sadighi, and M. R. Bagheri, “Low-velocity impact response of a nanocomposite beam using an analytical model,” Latin American Journal of Solids and Structures, vol. 12, no. 2, pp. 333-354, 2015. [https://doi.org/10.1590/1679-78251346]
• P. R. S. Reddy et al., “Influence of nanoclay and incident energy on impact resistance of S2-glass/epoxy composite laminates subjected to low velocity impact,” Advanced Material Letters, vol. 8, pp. 174-179, 2016. [https://doi.org/10.5185/amlett.2017.6473]
• J. N. Reddy, “A simple higher-order theory for laminated composite plate,” Journal of Applied Mechanics (ASME), vol. 51, no. 4, pp. 745-752, 1984. [https://doi.org/10.1115/1.3167719]
• J. M. Whitney and N. J. Pagano, “Shear deformation in heterogeneous anisotropic plates,” Journal of Applied Mechanics, vol. 37, no. 4, pp. 1031-1036, 1970. [https://doi.org/10.1115/1.3408654]
• H. D. Kang and K. C. Ahn, “A study on the dynamic behaviour of the coating tempered glass plate under impact,” International Journal of Mechanical and Production Engineering Research and Development (IJMPERD), vol. 8, no. 6, pp. 193-200, 2018. [https://doi.org/10.24247/ijmperddec201823]
• K. C. Ahn, “A comparative study on the impact behaviour of the coated glass plates by FSDT and HSDT,” International Journal of Mechanical and Production Engineering Research and Development (IJMPERD), vol. 8, no. 6, pp. 479-486, 2018. [https://doi.org/10.24247/ijmperddec201851]
• M. Chan, K. Lau, T. Wong, M. Ho, and D. Hui, “Mechanism of reinforcement in a nanoclay/polymer composite,” vol. 42, no. 6, pp. 1708-1712, 2011. [https://doi.org/10.1016/j.compositesb.2011.03.011]
• L. P. Kollar and G. S. Springer, Mechanics of Composite Structures, Cambridge University Press, 2003. [https://doi.org/10.1017/CBO9780511547140]
• R. Olsson, “Closed form prediction of peak load and delamination onset under small mass impact,” Composite Structures, vol. 59, no. 3, pp. 341-349, 2003. [https://doi.org/10.1016/S0263-8223(02)00244-1]
• R. Olsson, “Analytical model for delamination growth during small mass impact on plates,” International Journal of Solids and Structures, vol. 47, no. 21, pp. 2884-2892, 2010. [https://doi.org/10.1016/j.ijsolstr.2010.06.015]