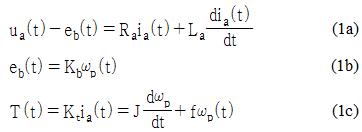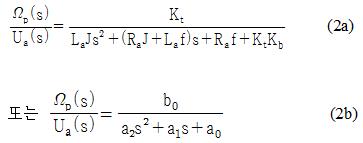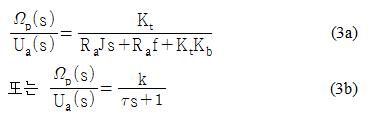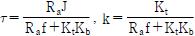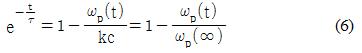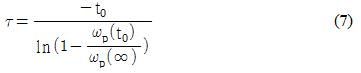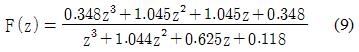GA-based parameter identification of DC motors

1. 서 론

산업 현장에서는 아직도 PID 제어기가 산업공정을 비롯한 석유, 화학 등의 다양한 분야에서 많이 이용되고 있다[1]. 이것은 구조가 단순하여 하드웨어적으로 실현하기가 쉽고 동조할 파라미터의 수가 적어 다루기가 용이하기 때문이다. 경험적이고 실험적인 제어기 설계기법들의 문제점을 보완하면서 불확실한 시스템의 PID 제어기의 파라미터를 결정하기 위한 다양한 설계방법이 제안되어 왔다[2]-[4]. 일반적으로 PID 제어기의 파라미터를 결정하기 전에 제어대상의 전달함수를 구하는 과정이 선행되어야 하는데 본 논문에서는 속도제어가 비교적 쉽고 로봇분야뿐만 아니라 다른 여러 분야에서 폭넓게 사용되고 있는 DC 모터의 파라미터를 추정하는 문제를 다룬다. 기존에 연구로 GA를 이용하는 방법[5][6], PSO(Particle swarm optimization)와 OLS(Orthogonal least squares)를 이용하는 방법[7], 신경회로망을 이용하는 방법[8]등이 제안되어 왔으나 이들 연구 대부분은 DC 모터를 수학적 모델로 간주하여 파라미터를 추정하는 한계점을 가지고 있다. 따라서 본 논문에서는 실제 실험장치의 입출력 데이터를 이용하여 파라미터를 추정하기로 한다.

실제 사용된 실험 장치는 Feedback 사의 "Precision servo workshop 33-008"이며, Matlab Simulink 기반으로 동작된다. 본 논문에서는 DC 모터의 파라미터 추정을 위해 두 가지 방법을 이용하였는데 첫 번째는 실제 데이터를 수치적 해석을 통하여 추정하는 방법이고, 두 번째는 최적화 알고리즘의 하나인 유전알고리즘(Genetic Algorithm; GA)[9][10]과 모델조정기법(Model adjustment technique)을 이용하는 것으로 실제 데이터와 조정모델 사이의 오차의 합이 최소가 되도록 GA를 통하여 최적화 하는 방법이다.

제안한 파라미터 추정 기법을 통해 얻어진 추정 모델은 실제 장치의 실험 데이터와 비교하여, 그 유효성을 살펴본다.

2. DC 모터 시스템

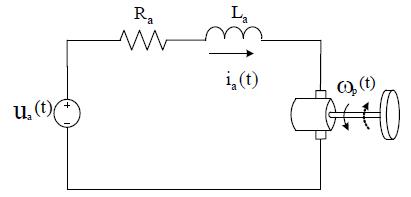
DC 모터의 구조는 크게 계자(Stator)와 전기자(Armature)로 구분할 수 있으며 전동기의 등가 회로는 Figure 1과 같이 표현된다. 계자는 전동기의 내부에 일정한 자기장을 만드는 역할을 하고, 전기자는 외부로부터 전류를 공급받아 회전자계를 만들며, 여기에는 구동권선이 이용되고 있다. 전기자에는 연속적으로 전류를 공급하기 위해 브러시(Brush)와 정류자(Commutator)가 있으며, 브러시는 전원으로부터 공급되는 전류를 정류자에 보내고 정류자는 브러시에서 공급되는 전류를 일정한 방향으로만 흐르게 한다.

Figure 1:

Equivalent circuits of a DC motor

속도제어의 목적은 전기자에 인가해 주는 입력전압 u_{a (t)}를 조절하여 전동기의 출력 각속도 ω_p (t)를 희망하는 값으로 조정하는 것이다.

Figure 1과 같이 등가회로로 표현되는 전기자 전압제어 직류 전동기의 관계식을 정리하면 다음과 같다.

여기서 R_a는 전기자 저항, L_a는 전기자 인덕턴스, K_b는 역기전력 상수, K_t는 토크상수, J는 회전자의 관성모멘트, f는 마찰계수이다.

식 (1)을 라플라스 변환하고, 정리하여 전달함수로 나타내면 다음과 같다.

여기서 a₀ = R_af + K_tK_b, a₁ = R_aJ + L_af, a₂ = L_aJ, b₀ = K_t을 의미한다.

한편, 일반적으로 L_a는 매우 작은 값이므로 무시하면 식 (2)는 다음과 같은 일차식으로 표현하는 것도 가능하다.

여기서 를 의미한다.

3. DC 모터의 파라미터 추정

본 연구에서 사용한 실험장치인 Feedback 사의 “Precision servo workshop 33-008”은 DC 모터, 모터 구동용 증폭기, 속도 센서(Tacho generator), 전압 공급장치(Power supply)등으로 구성되어 있으며 Figure 2는 실제 모습을 나타낸 것이다.

Figure 2:

DC motor system

식 (2a) 또는 식 (3a)로 표현되는 DC 모터의 전달함수에 나타난 각종 상수의 값을 정확히 측정할 수 있다면 정확한 DC 모터의 수학적 모델을 얻는 것이 가능하지만, 실제 상황에서는 그렇지 못한 경우도 있을 수 있다.

따라서 본 논문에서는 전달함수의 각 상수는 정확히 알 수 없으나 식 (2b) 또는 식 (3b)과 같이 전달함수 전체를 구할 수 있는 다음과 같은 두 가지 방법을 이용한다.

3.2 GA를 이용한 방법

유전알고리즘(GA)은 1975년 J. H. Holland가 제안한 것으로 “우성생식”과 다윈의 “자연선택”을 알고리즘 형태로 구현한 최적화 탐색기법 중의 하나이다. 잠정적인 해 집단에서 육종(Breeding)과 선택(Selection)을 구현하기 위해 재생산, 교배, 돌연변이와 같은 유전연산자를 사용하여 개체를 개량하고[8], 이들 간에 정보 형성과 교환을 장려하여 집단내의 개체가 해에 가까워지도록 여러 방향으로 탐색을 실행한다.

GA는 사용되는 코딩방법에 따라 크게 이진코딩(Binary coding), 실수코딩(Real number coding), 기호코딩(Symbolic coding)의 3가지로 구분할 수 있고, 전통적으로 염색체를 표현하는데 가장 많이 사용되어온 방법은 이진코딩 표현법이다. 그러나 탐색공간이 크거나, 고정밀도의 해가 필요한 경우, 제약조건이 존재하면 염색체의 길이를 크게 해야 하고 이는 연산부담으로 나타나며, 경우에 따라서는 탐색을 불가능하게 한다[9]-[10]. 따라서 본 연구에서는 이러한 단점을 극복하고 제약조건이 있는 경우에도 적합한 실수코딩 유전알고리즘을 사용한다.

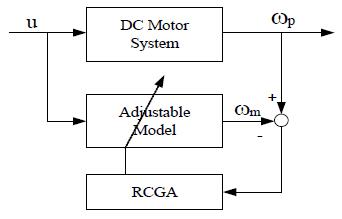
본 연구에서는 직류 전동기의 증폭기 앞에서 인가한 전압 와 출력인 회전속도의 데이터를 가지고 식 ( 2)와 식 (3)에 나타낸 전달함수를 구하기 위해 Figure 3과 같이 시스템과 모델을 병렬로 연결한 모델조정기법(Model adjustment technique)을 사용하기로 한다.

이때 조정모델을 실제 시스템과 일치시켜주기 위한 조정 메커니즘으로는 실수코딩 유전알고리즘을 이용한다.

Figure 3:

Parameter estimation of a DC motor

이때 사용되는 조정모델은 2차 시스템인 경우 식 (2b), 1차 시스템인 경우 식 (3b)를 사용한다.

이때 GA에 사용하는 목적함수에 따라 탐색 성능에 차이를 보일 수 있으므로 본 논문에서는 식(8)에 나타낸 것과 같이 IAE(Integral of the absolute error), ITAE(Integral of the time-multiplied absolute error), ISE(Integral of the square error)의 3가지 종류의 목적함수를 고려하기로 한다.

여기서 e(t) = ω_p (t) – ω_m (t)이며 ω_p (t)와 ω_m (t)는 각각 실제 실험장치와 조정모델의 회전속도이고, t_f는 최종 적분시간이다.

4. 시뮬레이션 및 실험 검토

본 논문에서 사용되는 실험장치는 Matlab Simulink 기반으로 동작되며, 장치에 설치된 센서를 통해 DC 모터에 인가되는 입력전압, 회전수 등을 측정할 수 있다.

4.2 Butterworth IIR 필터 설계

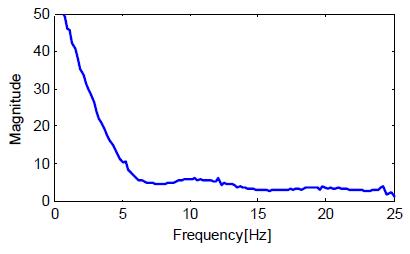
이때 측정신호의 잡음을 제거하기 위해서 Butterworth 저역통과 필터를 설계하기 위해 주파수 분석(FFT)을 시행하였으며, Figure 4는 이를 나타낸 것이다.

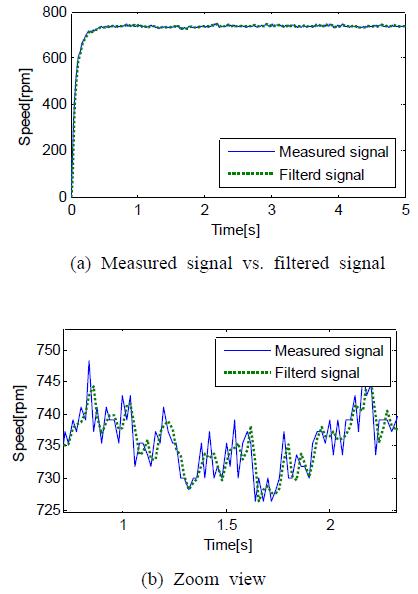
이를 통해 차단주파수(f_c)는 17Hz로 선정하였고, 3차 Butterworth 저역통과 필터를 설계하였다. Figure 5는 측정된 신호와 필터를 통과한 신호를 나타낸 것이고, 식 (9)는 설계된 Butterworth 저역통과 필터를 나타낸 것이다.

Figure 4:

FFT analysis

Figure 5:

Result of Butterworth IIR filter

4.3 수치적 방법

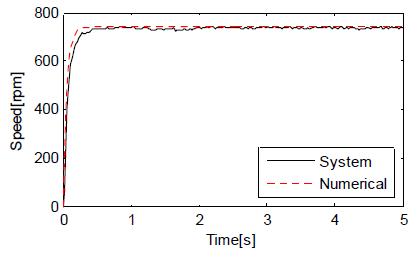
본 연구에서는 3.1절에서 설명한 방법과 필터링한 데이터를 이용하여 k와 τ를 결정하였으며, 그 값은 τ=0.0563, k=2059.73이었다. Figure 6에서 확인할 수 있듯이 수치적 방법을 통해 얻은 1차모델은 실제 실험 데이터와 대체적으로 잘 일치하고 있으나 실험 데이터와 오차는 약간 존재한다.

Figure 6:

Result of parameter estimation using numerical method

정량적으로 오차를 비교하기 위해 실험데이터와 수치적 방법을 통해 얻은 1차모델의 IAE를 계산하였으며, 그 값은 1855.664이었다. 이때 IAE= 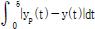이고, y_p는 실험데이터, y_p는 1차모델의 출력을 의미한다.

4.4 GA를 이용한 방법

3.2절에서 설명한 GA의 연산자는 산술적 교배와 동적 돌연변이, 엘리트 전략을 이용하였으며 집단의 크기는 80, 재생산계수는 1.8, 교배확률은 0.9, 돌연변이 확률은 0.02가 사용되었다.

이때 파라미터 탐색범위는 식 (2b)와 같은 2차 모델인 경우에는 0 ≤ a₀, a₁, a₂, b₀ ≤ 3, 식 (3b)와 같은 1차모델인 경우에는 0 ≤ k ≤4000, 0 ≤ τ ≤10이며 취득한 데이터를 이용하여 오프라인(Off-line)으로 파라미터를 추정한다.

Table 1은 GA를 이용하여 모터의 파라미터를 추정한 결과를 정리하여 나타낸 것이다.

Table 1:

Results of parameter estimation using GA

식 (8)의 3가지 목적함수를 이용하여 1차모델과 2차모델로 구분하여 파라미터를 추정하였으며 예상했던 것과 같이 2차모델인 경우 2차항의 계수는 매우 작은 값이 됨을 확인할 수 있다.

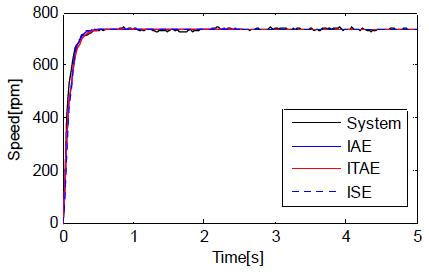
Figure 7은 GA를 통해 추정한 2차모델의 응답과 실제데이터를 나타낸 것이다. 그림에서 확인할 수 있듯이 GA를 이용해 추정한 2차모델은 실제 실험데이터와 잘 일치한다. Table 2는 3가지 종류의 2차모델의 성능을 정량적으로 비교하기 위해 5초간 실험데이터와 2차모델의 IAE를 계산한 것이다.

Figure 7:

Result of parameter estimation using GA method(2nd model)

Table 2:

Identification performances of 2nd order model

표를 통해 GA를 이용한 방법이 4.2절의 수치적 방법을 이용한 방법보다 더 정확한 파라미터 추정이 이루어지고 있음을 확인할 수 있다.

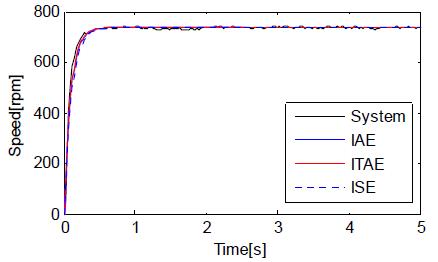
Figure 8은 GA를 이용해 추정한 1차모델의 응답과 실제데이터를 나타낸 것이다. 역시 1차모델의 성능을 정량적으로 비교하기 위해 5초 동안 실험데이터와 1차모델 사이의 IAE를 계산한 결과를 Table 3에 나타내었다. 그림과 표를 통해서 확인할 수 있듯이 GA를 통해 추정한 1차모델은 실제 실험데이터와 잘 일치하고 있다.

Figure 8:

Result of parameter estimation using GA method(1st model)

Table 3:

Identification performances of 1st order model

특히, 4.2절의 수치적방법과 GA를 이용해 추정한 2차모델 보다 더 정확한 파라미터 추정이 이루어짐을 확인할 수 있다. 이는 DC 모터 전달함수의 2차항의 계수 값이 매우 작아 1차모델과 같은 특성을 나타내기 때문으로 사료된다.

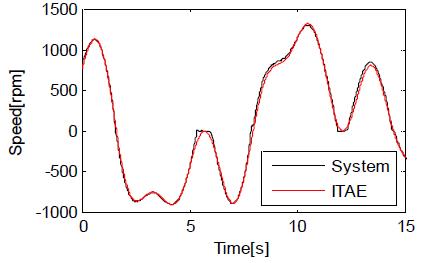
마지막으로 회전수가 다양하게 변하는 상황에서 실험결과와 추정모델의 응답을 비교하였다. Table 3에서 가장 작은 IAE 결과를 나타낸 1차모델을 대표적으로 선정하였으며, 이때 DC 모터에 인가된 전압 u = 0.031 + 0.42sin (0.5t) + 0.23sin (1.4t) + 0.15sin( (2.5t)이다.

Figure 9에서 확인할 수 있듯이 실험장치와 추정모델 사이에 약간의 시간지연이 존재하지만 대체적으로 잘 일치하는 것을 확인할 수 있으며 6[s]와 12[s] 부근에서 모델의 출력은 부드러운 곡선으로 표시되나 실제 실험장치의 회전속도가 0인 것은 실험장치의 각종 점성마찰 또는 쿨롱마찰에 의한 것으로 생각된다.

Figure 9:

Result of parameter estimation in the case of random input

5. 결 론

본 연구에서는 실제 실험장치(Feed back 사의 "Precision Servo workshop 33-008")의 입출력 데이터를 사용하여 시스템 파라미터를 추정하는 문제를 다루었다. 이를 위해 우선 출력 데이터의 잡음을 제거하기 위해 Butterworth IIR 필터를 설계하였으며, 필터를 통과한 데이터를 사용하여 수치적 해석방법과 GA를 이용한 방법 두 가지로 DC 모터의 수학적 모델을 추정하였다. 특히, GA를 이용한 방법은 1차 및 2차모델에 대해 3가지 평가함수가 최소가 되는 관점에서 파라미터 추정을 실시하였다.

제안한 방법을 통해 추정된 DC 모터의 수학적 모델은 서로 약간의 차이가 있었으나 실제 실험 데이터와 거의 동일한 출력을 보이고 있음을 확인하였다.

References

• Y. Nozaka, “Trend of new control theory application in industrial process control (survey)”, Proceedings of International Federation of Automatic Control 12th Triennial World Congress, 4, p215-218, (1993).
• K. J. Astrom, and T. Hagglund, “Automatic tuning of simple regulators with specifications on phase and amplitude margins”, Automatica, 20, p645-651, (1984).
• T. Yamamoto, M. Kaneda, T. Oki, E. Watanabe, and K. Tanaka, “Intelligent tuning PID controllers”, Proceedings of IEEE International Conference on Systems, Man, and Cybernetics, 5, p2610-2615, (1995).
• E. H. Bristol, “Pattern recognition: an alternative to parameter identification in adaptive control”, Automatica, 13, p197-202, (1977). [https://doi.org/10.1016/0005-1098(77)90046-2]
• A. Dupuis, M. Ghribi, and A. Kaddouri, “Multiobjective genetic estimation of DC motor parameters and load torque”, Proceedings of IEEE International Conference on Industrial Technology, 3, p1511-1514, (2004). [https://doi.org/10.1109/ICIT.2004.1490788]
• M. Lankarany, and A. Rezazade, “Parameter estimation optimization based on genetic algorithm applied to DC motor”, Proceedings of International Conference on Electrical Engineering, p1-6, (2007).
• M. S. A. Mohamad, I. M. Yassin, A. Zabidi, M. N. Taib, and R. Adnan, “Comparison between PSO and OLS for NARX parameter estimation of a DC motor”, IEEE Symposium on Industrial Electronics & Applications, p27-32, (2013). [https://doi.org/10.1109/ISIEA.2013.6738962]
• I. F. EI-Arabawy, H. A. Yousef, M. Z. Mostafa, and H. M. AbduIkader, “Parameters estimation of nonlinear models of DC motors using neural networks”, Proceedings of 26th Annual Conference of the IEEE Industrial Electronics Society, 3, p1997-2000, (2000).
• G. Jin, and S. Joo, “A study on a real-coded genetic algorithm”, Journal of Control Automation and Systems Engineering, 6(4), p268-275, (2000).
• G. G. Jin, Genetic Algorithm and It’s Application, Kyowoosa, (2000).