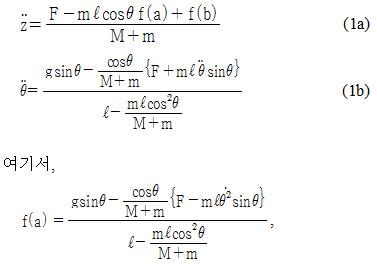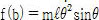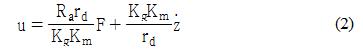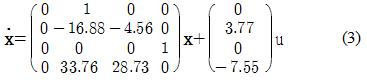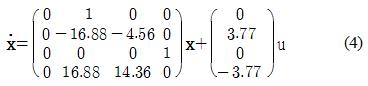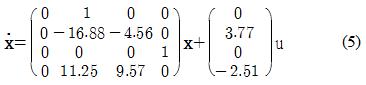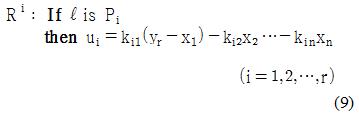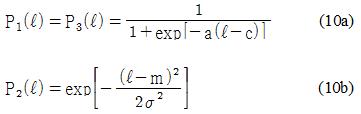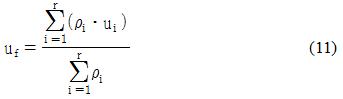Fuzzy-based adaptive controller for nonlinear systems

1. 서 론

비선형 시스템을 제어하는 일반적인 방법은 해당 시스템이 가장 많이 동작되는 평형점(Operating point) 부근에서 선형화 한 후, PID 제어기나 LQ 제어기와 같은 선형제어기를 설계하여 제어하는 것이다. 그러나 이러한 선형제어기는 제한된 제어환경 내에서는 우수한 제어성능을 발휘하지만, 제어환경 변화로 인한 파라미터의 변동이 존재하는 경우에는 강인성을 보장할 수 없고, 만족스러운 제어성능을 얻지 못하는 결점을 가지고 있다. 이러한 문제점을 해결하기 위하여 현재까지 많이 응용되어 온 기준모델적응제어(Model reference adaptive control; MRAC)와 자기조정제어(Self-tuning control) 등도 시스템의 결정적 성질에 의존하므로 제한된 제어환경에서만 성공적으로 작동하는 한계를 가지고 있다[1][2]. 이에 대한 하나의 대안으로 이[3]등은 비선형 시스템을 여러 개의 서브시스템으로 선형화하고, 각 서브시스템에 대해 서브제어기를 설계한 후 보간법을 이용해 융합하는 보간 기반 적응제어기를 제안하였다. 이를 통해 시스템의 파라미터 변화에 잘 대응하지 못하는 선형제어기의 단점을 보완하는 방법을 보였다.

한편, 퍼지제어는 불확실한 정보를 다룰 수 있고, 전문가의 지식을 직접 언어규칙으로 표현할 수 있으며, 제어대상의 수학적 모델을 요구하지 않는 장점 때문에 복잡하고 불확실한 시스템의 제어에 많이 이용되어 왔다[4][5]. 특히, T-S(Tagaki-Sugeno) 퍼지모델[6]과 병렬분산보상(parallel distributed compensation : PDC) 개념[7]을 이용한 비선형 시스템의 제어는 안정도 분석과 체계적인 설계방법이 가능해 많이 사용되고 있다.

따라서 본 논문에서는 제어환경의 변화에 대해 제어기에 적응성능을 부여하기 위한 또 하나의 방법으로 퍼지 기반 적응 제어기 설계기법을 제안한다. 이 방법은 비선형 시스템을 파라미터 변화에 따라 여러 개의 서브시스템으로 선형화 한 후, 서브제어기를 설계하고, PDC 개념을 이용하여 서브제어기를 다시 퍼지결합하는 방법이다.

제안한 제어기 설계 기법을 비선형 시스템이면서 구조적으로 불안정한 도립막대 시스템에 적용하여 시뮬레이션을 실시하고, 이를 기존의 선형 및 보간 기반 제어기와 비교함으로써 제어기의 유효성을 살펴본다.

2. 비선형 도립막대 시스템

2.1 대차와 도립막대

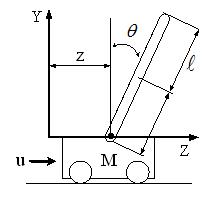
본 논문에서 다루는 비선형 시스템은 Figure 1과 같은 도립막대 시스템이다.

Figure 1:

Inverted pendulum system

그림에서 대차의 수평방향 위치를 z[m], 대차의 수평방향 속도를 [m/s],막대의 수직에 대한 각도를 θ[rad], 각속도를 [rad/s]라 정의하고, 라그랑지(Lagrange) 운동방정식을 이용하면 다음과 같은 비선형 운동방정식을 얻을 수 있다.

이고, M과 m은 각각 대차와 막대의 질량, 2l은 막대의 전체 길이를 의미한다.

2.2 대차 구동부

조금 더 실제적인 운동방정식을 구현하기 위해 위의 운동 방정식에서 대차에 가해지는 힘 F[N]와 구동 모터에 인가되는 전압 u[V]의 관계를 다음과 같이 구한다.

여기서 K_g는 기어박스의 기어비, r_d는 구동모터 피니언의 회전반경, K_m은 모터의 토크상수, R_a는 모터 회전자 저항을 의미한다. 이때 포화 구동 전압 u_sat는 구동 모터의 사양을 고려하여 ±20[V]로 가정한다.

한편, 시스템의 상태변수 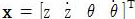으로 정의하고, 도립막대 시스템에 사용되는 파라미터는 Table 1과 같다.

Table 1:

The value of system parameters

3. 제어기 설계

2.2 퍼지 기반 적응 제어기

퍼지 로직은 제어 관점에서는 복수개의 “If-then” 형식으로 나타나는 서브제어기를 병렬로 퍼지추론하여 복잡한 입·출력 관계를 실현하는 것이 가능하므로 파라미터 변화에 대해 적응성을 부여하는 것이 가능하다.

본 논문에서 다루는 퍼지 기반 적응 제어기는 Takagi-Sugeno의 추론법을 응용하여 다음과 같이 추론한다.

여기서, Rⁱ는 i번째 제어규칙, r은 규칙의 개수로 3이고, u_i는 서브제어기 출력, k_ij(i=1,2,3;j=1,2,3,4)는 j번째 상태 변수에 대한 i번째 서브제어기의 이득이다.

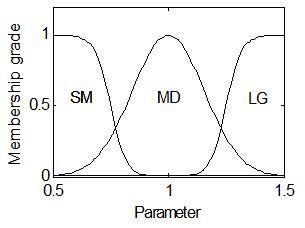
또한 P_i(i=1,2,3)는 전건부의 퍼지집합으로 식 (10)과 같은 시그모이드 및 가우시안형을 사용하였으며 P₁은 SM(Small), P₂는 MD (Medium), P₃는 LG(Large)를 의미한다.

Figure 3은 식 (10)을 이용하여 l의 변화에 따른 전건부의 퍼지 소속함수를 나타낸 것이다.

Figure 3:

Membership function

그러면 최종적으로 퍼지 기반 적응 제어기의 출력 u_f는 다음과 같이 추론된다.

여기서, ρ_i는 i번째 소속함수의 기여도이다.

4. 시뮬레이션

제안한 제어기의 성능 확인하기 위해 사용되는 도립막대 시스템은 식 (1)과 식 (2)의 비선형 시스템이다.

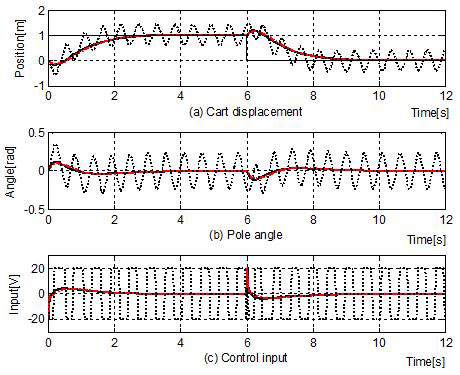
우선, 파라미터 변화(모델링의 불확실성)에 대한 적응성을 시뮬레이션 하기 위해 파라미터 l이 공칭모델인 길이 1.0[m]에서 +60% 증가(1.6[m])한 경우를 가정한다. Figure 4는 퍼지 기반 적응 제어기(FAC), 비교목적으로 기존에 연구[3]된 보간 기반 적응 제어기(IAC)와 l=1.0(가운데 길이)에서 설계된 LQ 제어기(LQC)의 응답을 나타낸 것이다.

Figure 4:

Responses using the FAC(black color), IAC(red color), LQC(dotted) in the case of l=1.6[m]

Table 2는 각 방법의 성능을 정량적으로 비교하기 위해 6[s]까지 대차의 오버슈트(M_p), 도달시간(t_r), 2% 정정시간(t_s), 막대 각도의 IAE를 계산한 결과이다. 이때 t_r= t₉₀—t₁₀이고, t₁₀과 t₉₀은 각각 출력이 설정치의 10%와 90%에 도달하는데 걸리는 시간을, 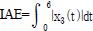를 의미한다. 표에서 보면 막대의 길이가 길어진 경우 FAC는 IAC와 거의 동일한 성능을 보인다. 특히 LQC는 파라미터 변화에 적응하지 못하고, 제어입력의 포화로 인해 심하게 헌팅하고 있다.

Table 2:

Control performances in the case of l=1.6[m]

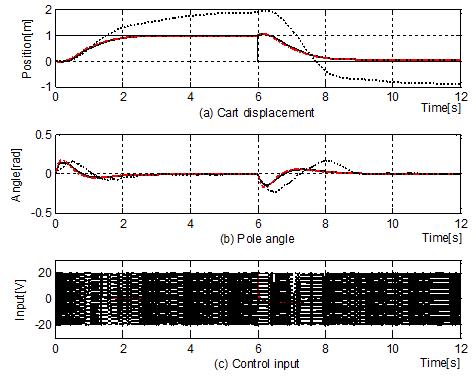
이제, 공칭모델(l이 1.0[m])에서 파라미터가 -60% 감소(0.4[m])한 경우를 가정한다. Figure 5에서 확인할 수 있듯이 FAC는 막대 길이가 짧아져 제어환경이 열악한 경우에도 강인한 제어성능을 보이고 있다. 이 경우에도 정량적 성능을 비교하기 위해 Table 2와 동일한 방법으로 제어성능을 구해 나타낸 것이 Table 3이며, 표를 통해 확인할 수 있듯이 FAC와 IAC는 거의 동일한 결과를 보이며, LQC는 제어입력 포화로 인해 심한 헌팅을 보이며 대차의 위치를 추종시키지 못하고 있다.

다음으로 공칭모델에서 파라미터 l이 범위 [0.5 1.5] 사이에서 l = 0.3sin(2t) + 0.3sin(1.5t) + 0.97와 같이 실시간으로 변화하는 상황에서 외란이 동시에 인가되는 경우의 제어성능을 살펴본다.

Figure 5:

Responses using the FAC(black color), IAC(red color), LQC(dotted) in the case of l=0.4[m]

Table 3:

Control performances in the case of l=0.4[m]

주어지는 외란은 각도 외란으로 가정하여 1[s] 시점에서 –0.1[rad], 7[s] 시점에서 +0.1[rad]을 인가하였고, 16[s] 시점과 22[s] 시점에서는 조금 더 큰 외란인 –0.2[rad]과 +0.2[rad]을 각각 인가하였다.

Figure 6는 이에 대한 응답 결과를 나타낸 것이고, Table 4는 15[s]까지의 대차에 대한 오버슈트(M_p), 도달시간(t_r), 2% 정정시간(t_s), 30[s]까지의 막대의 각도에 대한 IAE를 계산한 결과이며 각 방법의 외란 억제 성능을 정량적으로 계량하기 위하여 네 번의 외란을 인가할 때마다 응답의 피크치(Perturbance peak) M_peak와 외란의 영향이 소멸되는데 걸리는 회복시간(Recovery time) t_rcy을 동시에 구하였다. 이때 M_peak는 |max(x₃)—x_3s| 또는 |min(x₃)—x_3s|를 의미하고(x_3s는 막대의 각도가 0인 상태), t_rcy는 x₃가 x_3s의 2% 이내로 회복되는데 걸리는 시간을 의미한다. 이 경우에도 Table 4와 Figure 6을 통해 확인할 수 있듯이 FAC와 IAC는 약간 차이는 나지만 거의 동일한 결과를 보인다.마지막으로 Figure 6과 동일한 파라미터 변화 조건에 N(0, 0.01²)의 백색잡음(white gaussian noise)이 인가되는 경우를 살펴본다. 이때 백색 잡음은 실제 실험장치의 계측을 고려하여 대차의 위치와 막대의 각도 두 곳에 동시에 추가하였으며 Figure 7은 이에 대한 응답 결과를 나타낸 것이다.

Figure 6:

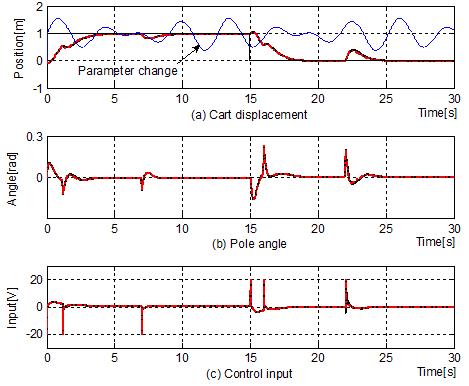
Responses using the FAC(black color), IAC(red color) in circumstances of parameter change and disturbance

Table 4:

Control performances in circumstances of parameter change and disturbance

Figure 7:

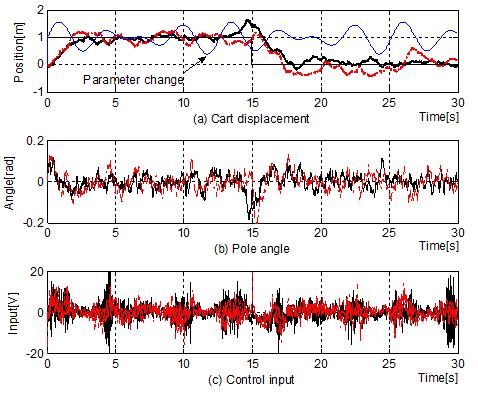
Responses using the FAC(black color), IAC(red color) in circumstances of parameter change and white gaussian noise

Table 5는 두 방법의 성능을 정량적으로 비교하기 위해 30[s]까지 대차와 막대 각도의 IAE를 계산한 결과이다.

Table 5:

Control performances in circumstances of parameter change and white gaussian noise

그림과 표를 통해 알 수 있듯이 FAC는 파라미터가 실시간으로 변화하고, 잡음이 주어지는 열악한 제어환경에서도 강인한 제어성능을 보이고 있다. 특히, 이 경우에는 대차의 추종 및 각도 유지 성능 면에서 FAC가 기존의 IAC 보다 우수한 결과를 보이고 있음을 확인할 수 있다.

5. 결 론

본 논문에서는 비선형 시스템의 제어를 위한 퍼지 기반 적응 제어기법을 제안하였다. 제안한 기법은 비선형 시스템을 파라미터 변화에 따라 다수 개의 선형 서브시스템으로 표현하고, 이 서브시스템에 대해 설계된 서브제어기를 퍼지규칙을 이용하여 융합한 제어기이다. 이렇게 서브제어기를 퍼지기법으로 결합함으로써 퍼지제어의 큰 장점인 강인성과 적응성을 가질 수 있게 된다.

제안한 기법은 비선형 도립막대 시스템에 적용하고, 기존의 제어기와 비교하여 시뮬레이션을 실시한 결과 다양한 형태의 파라미터 변화, 외란의 인가, 계측잡음을 고려한 제어환경에 대해 기존의 선형 및 적응 제어기보다 적응성과 강인성이 뛰어남을 확인할 수 있었다.

References

• R. E. Skelton, Dynamic Systems Control, John Wiley & Sons, (1988).
• M. Drouin, H. H. Kandil, and M. Marition, Control of Complex System, Plenum Press, (1991).
• Y. H. Lee, J. K. Ahn, G. G. Jin, and M. O. So, “Interpolation-based adaptive LQ control for nonlinear systems,”, Journal of the Korean Society of Marine Engineering, 32(4), p618-623, (2008), (in Korean). [https://doi.org/10.5916/jkosme.2008.32.4.618]
• S. Tong, T. Wangn, and J. T. Tang, “Fuzzy adaptive output tracking control of nonlinear systems”, Fuzzy Sets and Systems, 111(2), p169-182, (2000).
• I. Rojas, H. Pomares, J. Gonzalez, L. J. Herrera, A. Guillen, F. Rojas, and O. Valenzuela, “Adaptive fuzzy controller: Application to the control of the temperature of a dynamic room in real time”, Fuzzy Sets and Systems, 157(16), p2241-2258, (2006). [https://doi.org/10.1016/j.fss.2006.03.006]
• T. Takagi, and M. Sugeno, “Fuzzy identification of systems and its application to modeling and control”, IEEE Transactions on Systems, Man and Cybernetics, 15(1), p116-132, (1985). [https://doi.org/10.1109/TSMC.1985.6313399]
• K. Tanaka, and M. Sano, “A robust stabilization problem of fuzzy control systems and its application to backing up control of a truck-trailer”, IEEE Transactions on Fuzzy Systems, 2(2), p119-134, (1994). [https://doi.org/10.1109/91.277961]