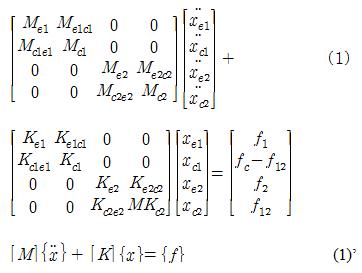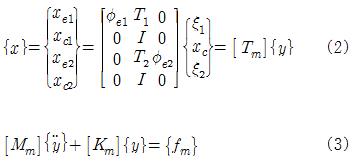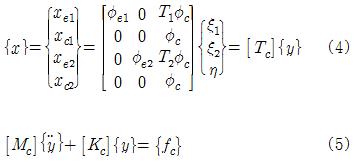Sub-structure mode synthesis vibration analysis program development using Matlab

2.1 부분구조 모델과 운동방정식

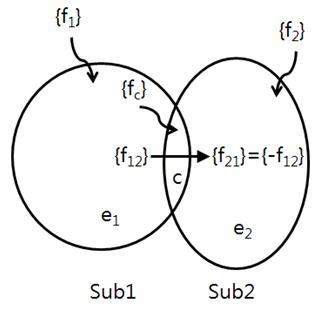
설명을 간단히 하기 위하여 구조물을 Figure 1과 같이 제일 단순한 2개의 부분구조로 나누기로 하고 감쇠가 없는 경우로 가정하면 다음과 같은 수학 모델로 쓸 수 있다.

Figure 1:

FEM model with 2 sub-structures

여기에서 e는 결합부를 제외한 본체 부분이고, c는 다른 부분구조와 결합부를 나타내고, 숫자 1, 2는 부분구조 번호를 나타내고, {x}는 변위, {f}는 외력, {f₁₂}는 부분구조 사이에 주고받는 상호 작용력을 나타낸다.

2.2 Guyan의 정축소와 부분모드를 이용한 자유도 축소

식 (1)은 모델만 부분구조별로 한 것이기 때문에 이대로 해석한다면 오히려 해석의 자유도가 결합부의 자유도만큼 증가하여 해석상 이득이 전혀 없다.

그래서 Guyan의 정축소법[2]이 등장하게 되는데 Guyan의 정축소법을 이용하면 자유도가 결합부의 자유도로 축소되어 자유도가 대폭적으로 줄어들게 된다. 이 방법은 정적인 문제의 해법에는 수학적으로 완벽하기 때문에 문제가 없으나, 진동문제에 적용하면 고차로 갈수록 오차가 커진다. 이를 보완하기 위하여 Hurty [3]와 Benfield [4]가 부분구조별로 해석한 부분모드(component mode)를 이용하여 부분구조의 진동모드를 추가로 채용함으로써 오차를 현격하게 줄였고, Okuma et al. [5]은 결합부도 결합부의 진동모드를 이용함으로써 한층 더 자유도를 줄여서 구조물의 진동해석을 할 수 있게 하였다. Tran [6]은 결합부 모드(interface modes)를 써서 순환대칭 문제에 대하여 적용하였다.

여기에서는 Hurty와 Okuma가 제안한 두 가지의 부분모드합성법을 이용하여 진동방정식을 풀기로 한다. 이 방법을 이용하면 자유도는 다음과 같이 대폭적으로 축소된다.

먼저 Hurty의 방법은 다음과 같다.

여기에서 [T₁]과 [T₂]는 Guyan의 정축소 행렬이고, [φ_e]는 결합부를 완전 고정 상태로 가정한 부분구조의 고유진동모드 행렬이다. 또 [φ_e]와 {ξ}는 부분구조 해석에서 채용한 모드의 수와 같은 자유도를 가진다. 즉 두 개의 부분구조에서 채용한 부분모드의 수와 결합부의 자유도의 합으로 전체 구조물의 자유도가 축소되는 것이다. 식 (2)를 식 (1)에 대입하고 [T_m]^t를 앞에 곱하면 식 (3)과 같은 축소된 자유도의 운동방정식을 얻을 수 있고, 이를 푼 다음 식 (2)에 대입하면 원래의 변위를 구할 수 있다.

한편 Okuma는 결합부도 고유치 해석을 하여 저차의 십 수개의 모드만을 채용함으로써 다음과 같이 한층 더 자유도를 줄였다.

여기에서 [T₁], [T₂], [φ_e]는 앞에서 설명한 바와 동일하고, 추가하여 결합부의 모드 [φ_c]를 이용하여 결합부의 자유도를 축소한다. {η}는 결합부에서 채용한 모드 개수의 자유도를 가지며 이들의 총합으로 전체 구조물의 자유도를 축소하는 것이다. 식 (4)를 식 (1)에 대입하고 [T_c]^t를 앞에 곱하면 식 (5)과 같은 축소된 자유도의 운동방정식을 얻을 수 있고, 이를 푼 다음 식 (4)에 대입하면 원래의 변위를 구할 수 있다.

식 (3)과 식 (5)에서 외력을 {0}으로 하면 자유진동해석이 되어 고유진동수와 축약된 영역에서의 고유진동모드를 구할 수 있다. 이를 다시 식 (2)와 식 (4)에 대입하면 실제의 물리적 영역에서의 고유진동모드를 얻을 수 있다.

3.1 부분구조 진동해석 프로그램의 구성

프로그램의 흐름은 다음과 같다. 먼저 전체 구조물을 나누기 쉬운 몇 개의 부분구조로 나누고, 각 부분구조를 적당한 유한요소로 나눈다. 각각의 부분구조는 비결합부와 결합부로 나눈다. 각 부분구조물에 대하여 비결합부만의 고유치 문제를 풀고, 결합부는 모두 모아서 결합부만의 고유치 문제를 푼다. 만약에 구조물 사이가 스프링으로 연결되어 있으면 강결합으로 처리하지 않고 스프링을 부가하여 해석한다.

구조는 크게 각 부분구조의 데이터를 이용하여 결합 정보를 알아내는 선행 프로그램과 이를 이용하여 고유진동수와 고유진동모드를 구하는 프로그램과 주파수응답함수를 구하는 프로그램과 고유진동모드를 구하는 프로그램으로 구성된다.

3.1 프로그램의 구조

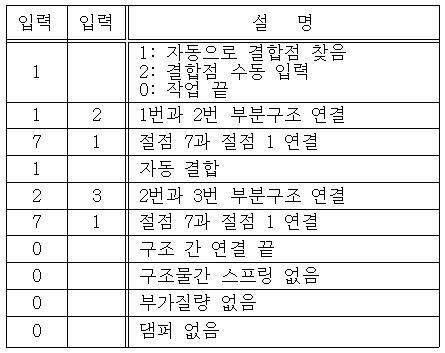
Figure 2는 결합 정보를 나타내는 excel 파일의 내용으로 메인 프로그램에 입력될 사항을 생성하기 위한 선행 프로그램의 입력 내용이다.

Figure 2:

Connection information between sub-structures for pre-processor in Excel file

Figure 3은 메인 프로그램의 입력 데이터를 생성하기 위한 선행 프로그램을 보인다. 부분구조 사이의 결합 정보는 좌표 비교를 통하여 연결점을 자동으로 찾는 방법과 수동으로 부분구조 사이의 연결 정보를 입력하는 두 가지 방법을 사용한다. 자동으로 찾을 경우는 구조물의 번호와 두 구조물이 서로 연결되는 대표점 한 점을 입력하면 나머지는 서로의 좌표를 비교하여 자동으로 찾아낸다.

Figure 3:

Pre-processor program to find connection information etc

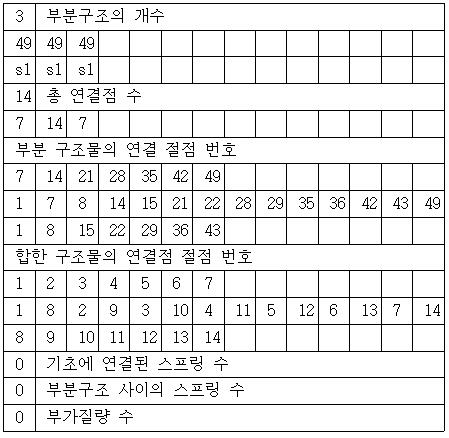
Figure 4는 선행 프로그램의 실행한 결과를 excel 파일로 출력한 결합정보로 메인 프로그램의 입력 데이터로 쓰인다. 부분구조물의 총 수효와 부분구 조물의 강성 행렬과 질량 행렬의 파일 이름, 각 부분구조물의 결합 점의 수, 결합 절점 번호, 결합 점의 전체 수와 이들을 번호 매김한 정보, 기반과 연결 여부, 구조물 사이의 스프링 개수, 부가 질량 부가 여부 등의 정보로 구성되어 있다.

Figure 4:

Connection information between sub-structures from pre-processor for main program

Figure 5는 메인 프로그램으로 선행 프로그램에서 얻은 정보를 이용하여 식 (3)이나 식 (5)를 풀어서 고유진동수를 구하고, 축소된 자유도 영역에서의 고유진동모드를 구하는 루틴을 보인다. ssm_main 프로그램은 Hurty의 방법이고, cms_main은 Okuma의 방법으로 사용자가 선택한다.

Figure 5:

Program for finding FRF

Figure 6은 모드 형상을 출력하는 프로그램으로 part를 ‘all’로 하면 모든 구조물을 하나의 그림으로 part를 ‘part’로 하면 부분구조 별로 출력을 해주도록 되어있다.

Figure 6:

Program to draw natural vibration modes

Figure 7은 주파수응답함수를 구하는 프로그램으로 가진점의 위치, 응답점의 위치, 주파수 범위와 츨력할 파일 이름을 입력하도록 되어있다.

Figure 7:

Program to draw natural vibration modes

이 예제에서는 1번 부분구조물의 1번 절점에 z방향으로 단위충격력이 가해졌을 경우(force=[1 1 3];), 1번 부분구조물의 1번 절점의 z방향 응답과 1번 구조물의 43번 절점의 z방향 응답과 2번 구조물의 25번 절점의 z방향 응답(resp=[1 1 3; 1 43 3; 2 25 3];)을 0.5Hz에서 500Hz까지 0.5Hz 간격으로 구하였다.

4.1 해석 모델

폭 300mm, 길이 900mm, 두께 5mm인 평판을 3등분 하여 300x300(mm²)인 정사각형 평판 셋으로 나누어서 개발한 프로그램으로 해석한다. 평판의 밀도는 7860kg/m³, 종탄성계수는 205GPa, Poisson 비는 0.3이고, 전혀 구속되지 않은 자유지지 상태로 해석하고, 실험에서 자유지지를 실현하기 위하여 철판에 작은 구멍을 두 곳에 뚫어서 공중에 매달아 철판에 수직인 방향은 거의 구속되지 않게 하여 실험한다.

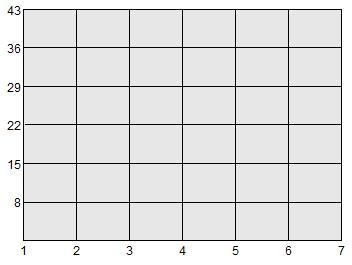
Figure 8은 하나의 부분구조를 보인다. 50x50(mm²)의 정사각형 요소로 분할하였고, 절점 번호는 그림과 같이 1~49로 부여하였다. 이와 똑같은 부분구조가 셋으로 된 되어있는 예에 대하여 적용한다.

Figure 8:

Sub-structure model

Figure 2는 선행 프로그램의 입력 데이터의 구조이다. 맨 처음의 1은 자동 결합점 찾기를 의미하고, 두 번째 줄의 1 2는 1번 부분구조와 2번 부분구조가 서로 연결되어 있다는 뜻이고, 세 번째 줄의 7 1은 1번 부분구조의 7번 절점과 2번 부분구조의 1번이 연결되어 있다는 의미이다. 다시 1은 또 자동 연결을 의미하고, 0이 나오면 더 이상 연결 정보가 없음을 의미하고, 또 마지막 세 줄의 0, 0, 0은 각각 기초에 연결된 스프링과 부분구조 사이의 스프링과 부가질량이 없다는 것을 의미한다. 만약 이들이 있으면 개수와 계수를 입력한다.

Figure 3은 선행 프로그램으로 변수 grid_dat은 입력 데이터 파일의 이름이고, 변수 ICOMP는 서로 모양이 다른 부분 구조의 개수이고, 따라서 이 예제 문제에서는 전부 모양이 같으므로 1이다. 변수 sub에는 부분구조의 데이터가 들어있는 Excel의 file의 sheet 이름이고, KM은 부분 구조의 강성행렬과 질량행렬의 파일 이름이고, IDMND은 구하고자 하는 고유진동수의 개수이다. 나머지 변수들은 출력 파일을 정의하므로 문제 별로 따로 폴더를 관리한다면 손대지 않아도 된다.

Figure 4는 선행 프로그램의 출력 결과로, 3개의 부분구조로 되어있고, 각 부분구조는 49개의 절점을 가지고 있으며, 1번 구조물은 7점이 2번 구조물과 연결되어 있는데 그 절점 번호가 7, 14, ... 49임을 알 수 있다. 2번 구조물은 14점이 연결되어 있고, 그 절점 번호가 1, 7, ... 49임 등을 알 수 있다. 또한 연결점에 대하여서는 1번부터 14번의 번호가 부여되는데 같은 번호는 부분구조가 서로 연결되어 있다는 것을 의미한다.

또 마지막의 0, 0, 0은 각각 기초에 연결된 스프링의 개수, 부분구조 사이의 스프링 개수, 부가질량의 개수 등을 의미하고, 만약 이들이 있으면 개수와 계수를 입력한다. 만약 부분구조 사이가 스프링으로 연결되어 있으면 연결점에 같은 번호를 부여하지 않고 다른 번호를 부여한다.

4.2 해석 결과

Table 1은 개발한 프로그램을 이용하여 계산한 고유진동수와 충격시험으로 구한 고유진동수를 비교한 것이다. exp는 실험결과이고, ssm은 Hurty의 방법으로 계산한 결과이고 cms는 Okuma의 방법으로 계산한 결과이고, err은 실험을 기준으로 한 오차율(%)을 나타낸다. 두 방법 모두 실험과 아주 잘 일치하는 것을 알 수 있다. 실험 결과는 단순히 주파수응답함수에서 피크 점을 읽은 결과이므로 곡선맞춤법 등으로 계산하면 더 잘 맞을 것으로 기대된다. 8차와 9차는 중근으로 여러 점을 이용하여 곡선맞춤법으로 계산하면 추출해 낼 수 있을 것이다.

Table 1:

Natural frequencies of the structure

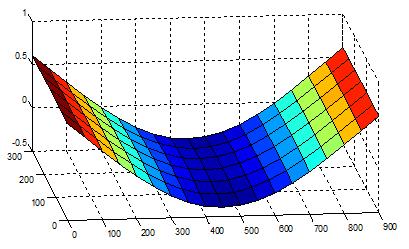
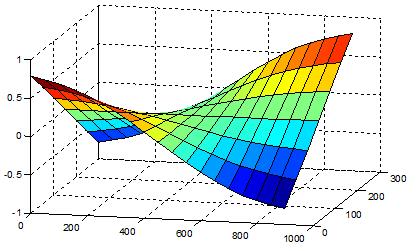
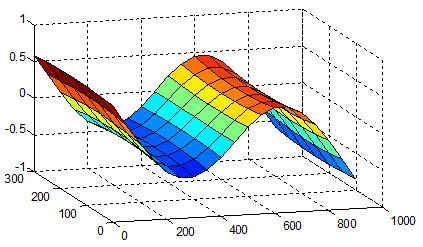
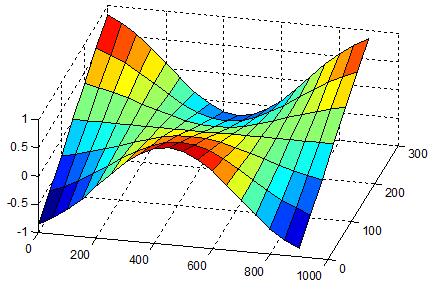
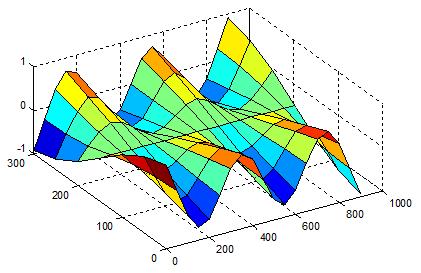
Figure 9 ~ Figure 12은 강체 모드를 제외한 구조물의 고유진동모드를 보인다. 예견할 수 있는 진동모드가 차례로 나타나고 있음을 알 수 있다. Figure 13는 보다 고차의 진동모드를 보이기 위하여 중간의 진동모드는 생략하고 14차의 고유진동모드를 보인 것이다.

Figure 9:

1st natural mode shape(1st bending mode) at 32.5Hz

Figure 10:

2nd natural mode shape(1st twisting mode) at 59.8Hz

Figure 11

3rd natural mode shape(2nd bending mode) at 90.4Hz

Figure 12

4th natural mode shape(2nd twisting mode) at 126.3Hz

4.3 해석 결과의 분석

Table 1에서 알 수 있듯이 고유진동수가 실험과 해석이 거의 완벽하게 일치함을 알 수 있고, Figure 9~Figure 13에서 알 수 있듯이 고유진동모드도 예상한 바와 같이 규칙적으로 잘 나타나고 있다.

Figure 13:

14th natural mode shape at 426.8Hz

Table 2는 구조물을 그대로 유한요소법을 적용했을 경우와 개발한 프로그램을 적용했을 경우의 자유도의 감소에 대한 것이다. 원 구조물의 자유도는 798이지만, 해석은 부분구조 별로 이루어졌기 때문에 294자유도에 대하여서만 해석하면 되고, 이들의 결과를 이용한 축약된 구조물의 자유도는 200에 불과함을 알 수 있다.

Table 2:

Degrees of freedom each part

실제의 구조물에 적용하면 이의 효과는 훨씬 더 극적으로 나타난다. 예를 들어 10,000점으로 분할된 구조물의 자유도는 60,000이지만, 이를 10개의 부분구조로 분할하면 각 부분구조의 자유도는 대략 6,000정도일 것(실제로는 결합점이 양쪽 구조물에서 다 같이 잡히기 때문에 수백 자유도 정도가 늘어남)이고, 각 부분구조의 채용 자유도는 여전히 20~50이면 충분하므로 축약된 모델의 자유도는 수 백으로 충분하게 된다. 개인용 계산기를 이용할 경우 메모리를 8GB로 하고, 가상 메모리를 늘여도 질량행렬과 강성행렬을 60,000*60,000으로 잡고 다른 변수들에 대하여서도 변수를 할당하면 계산이 불가능하게 된다. 그러나 제안한 방법을 이용하면 최대 부분구조의 자유도인 6,000*6,000 정도의 행렬 서너 개만 잡으면 되기 때문에 별 무리 없이 계산을 수행할 수 있다. 계산기의 용량 문제뿐이 아니고 당연히 행렬의 크기가 커지면 고유치 문제의 풀이 등 연산 과정에서 계산 시간도 기하급수적으로 늘어나게 된다.

해석에 사용된 구조물은 단순하기 때문에 고유진동모드를 하나의 그림으로 표시해도 좋으나, 구조물이 복잡한 경우에는 각 부분구조 별로 떼어내서 그림을 그릴 수 있다.