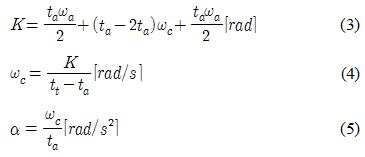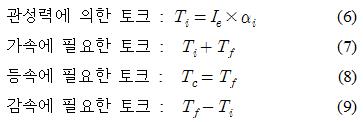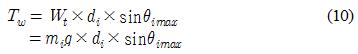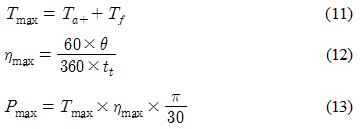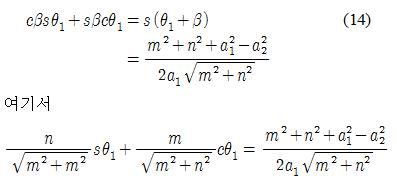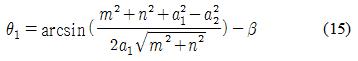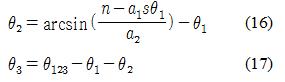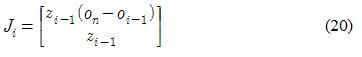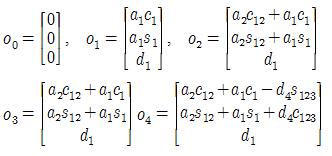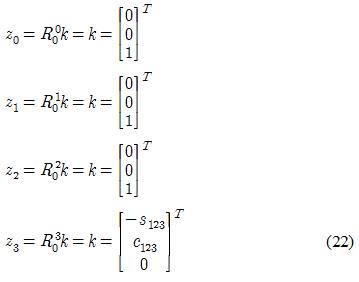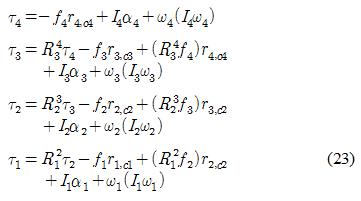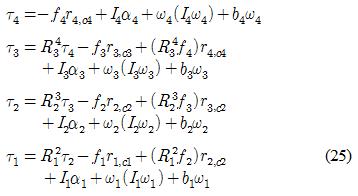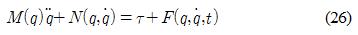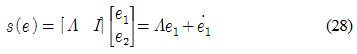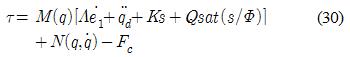A study on design, experiment control of the waterproof robot arm

1. 서 론

최근 산업용 로봇 외에 생활지원, 위험물처리, 소방방재 등의 다양한 목적의 로봇들이 연구되고 있다. 이러한 로봇들은 고정된 작업을 하는 산업용 로봇들과 달리 실내외 환경에서 이동하며 감시나 정찰을 하는 작업을 한다. 대표적인 로봇들로는 Packbot [1], Remotec-Andros robot [2][3], AZIMUT [4] 등이 있다. 이들은 이동하는 이동부와 작업을 하는 로봇팔로 크게 나눌 수 있다.

이들 로봇은 이동부에 로봇팔을 부착하여 동작하므로 대체로 경량이며 자유도가 낮은 것이 특징이다. 일반적인 집기와 놓기를 포함하는 유용한 동작이 가능한 로봇팔에 대한 설계연구를[5] 하였다. 이 연구에서는 양팔로봇을 제작하여 감각을 가지며 물체를 다루는 연구를 수행하였다. 이외에도 로봇팔의 다양한 집기 및 놓기, 이송, 최적 자세에 대한 연구[6]-[8]들이 있으며, 이동에 로봇팔을 사용하는 것에 대한 연구[9]와 안정된 카메라뷰를 얻기 위해 로봇팔을 설계한 연구[10], 그리고 로봇팔의 경량화를 위해 탄소섬유강화 플라스틱을 이용한 로봇팔의 설계에 대한 연구도 수행되었다[11]. 또한, 말단에 부착된 카메라를 이용하여 비전정보를 취득하고 이를 처리하는 연구도 수행되었다[12].

본 논문에서는 화재나 홍수로 인하여 침수된 건물 내부를 탐사할 수 있는 방수형 소형 4축 로봇팔을 설계하고, 이에 대한 기구학 및 동역학 해석을 수행한다. 침수된 좁고 극한 공간에서 다양한 임무와 탐사에 적합하도록 경량의 이동 플랫폼과 카메라를 장착할 수 있는 4축 관절 구조를 설계하고, 수심 10m의 방수 가능한 관절구동기를 설계하며, 이에 대한 순기구학 및 역기구학 해석을 수행한다. 또한, 뉴턴-오일러 방법에 의한 동역할 해석을 수행한다.

2. 로봇팔 기구부 구성

2.1 4축 로봇팔 기구 구조

좁고 물이 차있는 공간에서 다양한 임무와 탐사를 수행하는 경량의 이동 플랫폼에 설치하기 위한 4축 로봇팔의 설계 조건은 다음과 같다.

- 가반하중 2kgf, 총 무게 10kgf 내외의 소형경량 4축 구조

- 수심 10m 에서의 탐사 및 작업을 할 수 있는 방수설계

- 카메라의 동작반경을 극대화 할 수 있는 관절 구조

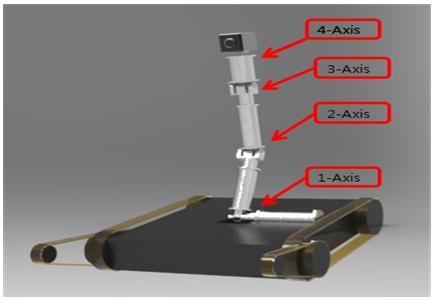
본 연구에서는 상기와 같은 설계사양을 만족하기 위한 설계를 수행하였으며, 로봇팔의 구조는 플랫폼과 결합하여 이동시, 카메라의 탐사공간을 최대한으로 하는 구조로 설계하였다. Figure 1은 이동로봇에 설계되어질 4축 로봇팔을 설치하는 개념도로 Pitch-Pitch-Pitch-Yaw 관절구조로 설계하였다. 또한 1축, 2축 및 3축의 관절구동기는 각각 ±70° 까지 동작이 가능하며, 4축은 카메라의 촬영이 용이하도록 360° 의 동작이 가능하도록 설계 하였다.

Figure 1:

Degree of freedom of the manipulator

각 모터 하우징을 포함하는 로봇 링크의 중량은 각각 2.5kgf, 2.5kgf, 2.5kgf, 2kgf로 제약조건을 설정하였다. 이에 따라 드라이버 및 배선을 포함하는 로봇팔의 총 무게는 약 10kgf으로 설정하고, 수심 10m 방수와 가반하중 2kgf의 조건을 충족하기 위한 설계를 수행하였다.

2.2 관절구동부의 구동용량 선정

방수형 로봇팔을 구동하는 각 축의 구동기 용량을 선정하기 위하여, 2.1절에서 설정한 제약조건을 바탕으로 각 축의 관절구동기 용량을 선정하였다.

용량의 선정을 위한 로봇팔의 파라미터(Parameter)는 제약조건에 따라 설정하였다.

Table 1은 각 관절의 링크 파라미터 값을 나타낸 것이다. a_i는 링크 직경, b_i는 링크 길이, d_i는 회전중심과 질량중심 거리, θ_i는 회전축을 중심으로 동작하는 각 변위를 나타낸다. m_i는 각 회전하는 링크의 질량이다.

Table 1:

Parameter of driving Joint

각 링크의 관성모멘트를 구하기 위해 다음의 네 가지 가정을 하였다.

(1) 구동축은 회전중심에 위치함

(2) 각 축의 최대변위 θ만큼 회전하는데 걸리는 회전시간은 0.5 s

(3) 가감속 시간은 0.15 s

(4) 회전축 마찰 저항 토크 T_n은 0.5 Nm

회전축(Z)가 질량중심과 일치 할 때 Z 축에 대한 관성모멘트는 다음과 같다.

회전축이 질량중심에서 거리가 d 만큼 떨어져 있을 때, Z축에 대한 관성모멘트 (I_ei)는

Table 2 는 식 (1) 및 식 (2)를 통해 구한 각 링크의 관성모멘트 값을 나타낸 것이다.

Table 2:

Moment of inertia of the joint

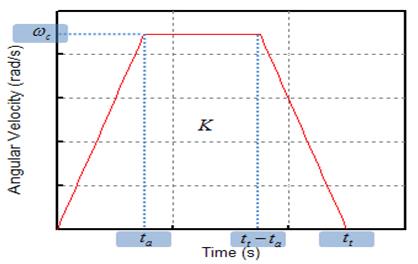
Figure 2의 그래프 내부면적은 각 관절의 총 회전각도 K(rad)와 같다. 각 관절구동기의 가감속 시간을 t_a(s)로, 총 구동시간을 t_t(s)라고 한다면 다음과 같은 식이 성립한다. 여기서 w_c는 각속도, α는 각가속도다.

Figure 2:

Time-angular velocity graph

Table 3은 식 (4) 및 식 (5)를 통해 구한 각 관절의 각속도, 각가속도 값을 나타낸 것이다

Table 3:

Angular velocity, acceleration

다음으로 각 관절구동기에 작용하는 토크는 가속, 등속, 감속 운동으로 나눌 수 있다.

Table 4는 위 식을 통해 얻어진 각 관절구동기의 구동토크이다.

Table 4:

Torque of the driving joints (I)

다음으로 로봇팔의 각 축에 무게로 발생하는 가해지는 중력방향의 부하토크 T_w는 다음과 같고 이를 통해 구한 값은 Table 5에 정리하였다.

Table 5:

Torque of the driving joints (W)

각 관절구동기에 부과되는 부하용량은 다음의 식들에 의해 계산된다.

Table 6은 위의 식에 따라 구동모터의 용량을 계산하여 나타낸 것이다.

Table 6:

Power of Driving joint

2.3 관절구동부의 방수 설계

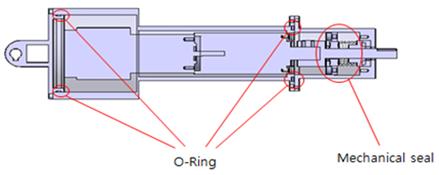
방수형 로봇팔의 설계에 있어서 어려운 문제 중의 하나는 관절축의 방수이다. 현재 모터 회전축의 방수에 사용되는 방법에는 오링과 메커니컬실을 이용한 것들이 있다. 메커니컬실은 조립을 하기 위한 공간과 마찰에 의한 부하 및 그에 따른 수명이 단축된다는 단점이 있으나 수중 10m 정도의 방수시스템에는 적합하다.

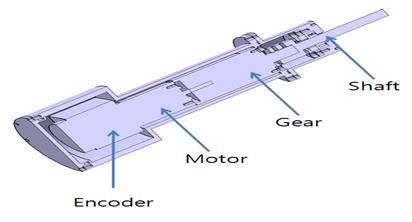
본 연구에서는 방수형 소형-경량화 로봇팔의 관절구동기는 직결구조로 설계하였다. Figure 3는 로봇 링크의 3D 모델링이고 Figure 4는 방수 설계에 대한 구조이다. 소형 및 경량화를 고려하여 로봇 관절부의 링크 내에 설치공간이 작고 조립 및 분해가 용이하다. 가벼운 메커니컬실을 적용하여 모터 회전축의 방수구조를 설계하고 관절구동기에 적용하였다.

Figure 3:

Cross section of motor housing

Figure 4:

Structure of waterproof housing

2.4 로봇 팔의 제작 및 10m 방수 시험

제약조건에 따라 부하용량 해석을 통해 선정한 구동기와 메커니컬실을 적용한 관절구동기의 하우징을 설계하였다. 관절구동기의 하우징을 링크의 일부로 구성하는 단순구조의 로봇팔을 설계함으로써 로봇팔의 경량화 설계를 하였다. Figure 5는 설계에 따라 직접 제작한 로봇팔의 사진이다.

Figure 5:

Developed 4-axis waterproof robot arm

제작한 로봇팔의 수밀성능을 시험하기 위하여 10m 깊이의 수조에서 방수시험을 하였다. 로봇팔의 각 축을 회전 동작시키며 방수시험을 하였다. 다음의 Figure 6, Figure 7 및 Figure 8 은 각각 1축, 2축, 3축, 관절구동기의 방수성능 시험장면을 나타낸다.

Figure 6:

Water proof test of 1st Actuator

Figure 7:

Water proof test of 2nd Actuator

Figure 8:

Water proof test of 3rd Actuator

시험 결과 10m 수심에서 축으로 물의 침투가 없는 방수성능을 확인하였다.

2.5 로봇 팔의 기구학적 해석

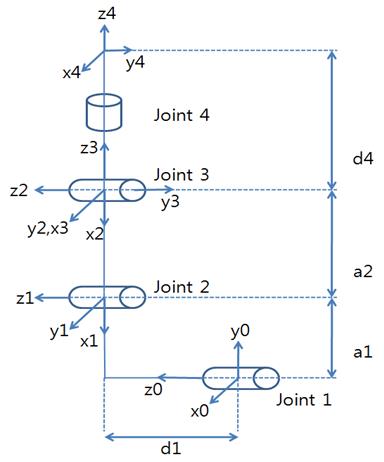
4축 로봇팔의 기구학 해석을 하였다. 지면에 고정되는 로봇팔의 1축을 기준축으로 설정하고, D-H (Denavit-Hartenberg)[13] 규약을 사용하여 Figure 9와 같이 좌표계를 설정하였다. D-H 규약에 따라 좌표를 설정한 후 a_i, α_i, d_i, θ_i에 해당하는 각각의 관절링크 파라미터를 구하고 순기구학 해석을 통한 링크 파라미터를 Table 7 에 정리하였다.

Figure 9:

D-H coordinate of 4-axis manipulator

Table 7:

D-H coordinate parameter of manipulator

여기서 a_i, α_i, d_i, θ_i는 임의의 링크 관절 i의 파라미터들이다. 구한 파라미터 값들을 이용하여 각각의 관절 링크에 대한 기본 변환 행렬을 순차적으로 곱하여 전체 변환행렬을 구한 결과를 정리하면 다음의 관계식들을 유도할 수 있다.

이고 이 식을 정리하면, 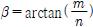이다. 여기서 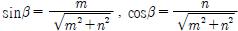이므로, 식 (14)를 정리하면 다음의 식을 구할 수 있다.

유사하게 식 (14)에서 다음을 구할 수 있다.

여기서 θ₁₂₃ = arcsin (―r₁₃)이며, 마지막으로 다음 식을 구할 수 있다.

3. 로봇팔의 동역학 해석 및 제어

설계한 4축 로봇팔의 동역학을 해석하기 위해 반복적 뉴턴-오일러 방법을 이용하였으며, 로봇팔의 각 링크에 가해지는 힘과 토크를 차례로 해석하여 직선운동과 회전운동을 나타내는 방정식을 유도하였다[14].

여기서 ω₀ = α₀ = a_c,0 = a_e,0 = [0 0 0]^Τ를 초기조건으로 설정하고 i를 1에서 n까지 증가시키며 연관 관계식을 구한다. 말단조건 f_n+1 = 0, τ_n+1 = 0으로 시작하여 순차적으로 f_i와 τ_i를 계산하여 정리하면 다음의 관계식을 유도할 수 있다.

뉴턴-오일러 방법에 의해 유도한 로봇의 운동방정식은 식 (23)과 같으나 본 연구에서는 일반 로봇과 달리 수중에서 동작 가능하도록 메커니컬실을 이용한 방수기능을 더하였다. 이 메커니컬실은 스프링의 면압에 의해 외부의 물이 모터 및 전자장치가 설치된 로봇 링크 내부로 유입되는 것을 방지하는 것으로 로봇관절의 동작에 마찰력을 일으키므로 식 (9)에 이의 모델링 식을 고려하여야 한다. 메커니컬실에 의한 마찰부하 f_r은 각 축에 대해 다음과 같이 표현된다.

여기서 회전 댐핑 계수 b_i의 크기는 메커니컬실의 면압에 비례하며 실험을 통해 구할 수 있다. 식 (24)를 포함하는 로봇 운동방정식은 다음과 같이 표현된다.

설계한 4축 로봇팔의 성능을 검증하기 위하여 본 논문에서는 로봇팔이 관절에서의 마찰토크와 같은 외란이 있음에도 불구하고 목표궤적을 잘 추종하도록 하기 위해서 외란에 강인한 슬라이딩모드 제어기를 설계하였다. 식 (25)를 간략한 n 링크 로봇팔 동역학 행렬식으로 다음과 같이 표현할 수 있다.

여기서 q∈R^N는 관절각도를 나타내는 벡터이고, M(q)는 관성행렬, 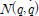는 코리올리항과 중력항을 나타내는 벡터이다. 또한 τ는 제어입력 벡터이며 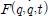는 관절에서 발생하는 마찰부하를 포함하는 외란 항이다. 이러한 외란항의 정확한 값을 알지 못하지만 일정한 범위 안에 존재한다고 가정한다.

본 논문에서 설계한 로봇팔에 적합한 슬라이딩모드 제어기[14]를 설계하기 위하여 식 (27)과 같은 오차벡터를 정의한다.

여기서 q_d는 각 관절의 목표궤적을 나타내는 벡터이다. 위의 정의를 이용하여 식 (28)와 같이 n차원의 슬라이딩평면을 정의한다.

설계한 제어기의 안정성 해석을 위해 슬라이딩평면의 시간에 대한 미분은 식 (29)와 같다.

여기서 제어이득 K > 0, Q > 0을 만족하는 양의 행렬이다. 따라서 로봇팔의 궤적추종을 위하여 외란에 대하여 강인한 성능을 나타낼 수 있는 슬라이딩모드 제어기는 식 (30)과 같다.

설계된 슬라이딩모드 제어기의 성능을 확인하기 위하여 각 관절에 대하여 LSPB 방법을 이용한 궤적을 생성하고 이를 추종하도록 하는 시뮬레이션을 수행하였다. 시뮬레이션에 사용된 로봇팔의 파라미터는 Table 1 에 나타낸 실제 로봇팔에 대한 파라미터를 사용하였으며, 슬라이딩모드 제어기에 사용된 파라미터는 Table 8과 같다.

Table 8:

Parameters of controller

관절에서의 마찰과 같은 외란이 존재할 때 슬라이딩모드 제어를 이용하여 강인한 궤적추종 성능이 다음과 같이 얻어짐을 알 수 있다.

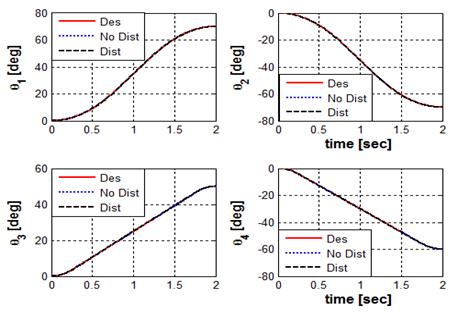
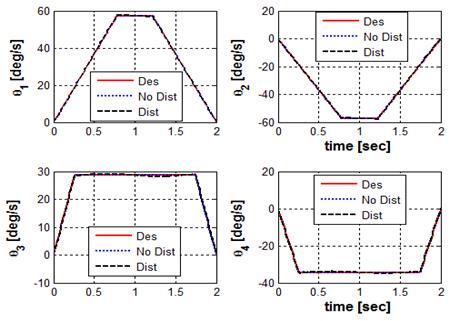
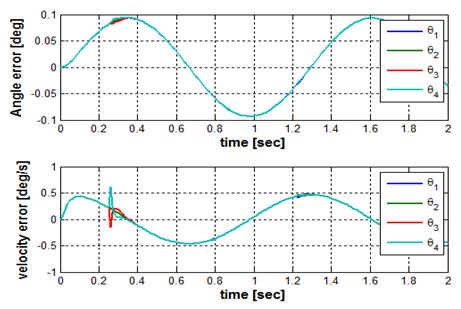
사인파 형태의 마찰 및 외란이 존재하는 경우에 슬라이딩모드 제어기를 이용하여 Figure 10과 같은 목표궤적을 추종하도록 시뮬레이션을 수행하였다. Figure 10은 외란이 없는 경우와 있는 경우에 대한 관절각도 추종 결과를 나타내고, Figure 11은 관절각속도의 추종결과를 나타낸다. 결과에서 보는 바와 같이 목표값을 큰 오차 없이 잘 추종함을 볼 수 있다. 또한 Figure 12는 각 관절의 목표각도와 실제각도 사이의 오차 그리고 목표각속도와 실제각속도 사이의 오차를 나타내는 그림이다. Figure 12의 결과에서 보는 바와 같이 외란이 있는 경우에도 관절각도에서는 0.1° 내의 오차를 가지고 목표궤적을 추종하고 있으며, 관절각속도는 0.5 °/s 의 오차 내에서 사다리꼴 형태의 속도프로파일을 잘 추종함을 보이고 있다. 이와 같은 시뮬레이션 결과를 바탕으로 슬라이딩모드 제어기의 성능을 확인할 수 있다.

Figure 10:

Joint angles

Figure 11:

Angular velocities

Figure 12:

Angle and angular veocity erros

4. 결 론

본 논문에서는 화재나 홍수로 인하여 침수된 건물 내부를 탐사할 수 있는 새로운 구조의 방수형 소형 4축 로봇팔을 개발하고 이의 기구학 및 동역학 해석을 하였다. 카메라를 장착할 수 있는 Pitch – Pitch – Pitch - Yaw 4축 구조로 설계했다. 그리고 각 관절 구동기에 가해지는 부하해석을 하고 이에 따라 구동기의 용량을 선정하였다. 또한, 수심 10m의 방수 가능하도록 메커니컬실을 적용하여 관절구동기를 설계 제작하여 10m 깊이의 수조에서 구동시험을 통하여 성능을 검정하였다.

또한 설계한 로봇팔의 D-H 방법에 의해 순기구학 및 역기구학 해석을 통해 닫힌 해를 유도하였고, 메커니컬실의 마찰력을 고려한 로봇팔의 운동방정식을 뉴턴-오일러 방법에 의해 유도하였다. 마찰과 같은 외란이 있는 개발 로봇팔이 목표궤적을 잘 추종할 수 있도록 슬라이딩모드 제어기를 설계하고 시뮬레이션을 통해 그 성능을 확인하였다.

향후 개발한 로봇팔의 실제 제어에 대한 실험을 수행할 계획이며, 이를 통하여 극한 환경에서 사용할 수 있는 방수형 로봇팔에 대한 적용 가능성을 확인할 계획이다.

Acknowledgments

본 논문은 특수재난현장 긴급대응기술개발사업단의 ‘특수재난지역 최첨단 정찰 및 원격제어 시스템 개발’의 연구기금으로 수행되었음.

References

• R. R. Murphy, “Activities of the rescue robot at the world trade center from 11-21 September 2001, IEEE Robotics & Automation Magazine, 11(3), p851-864, (2004).
• T. Frost, C. Norman, S. Pratt, and B. Yamauchi, “Derived performance metrics and measurements compared to field experience for the packbot,”, Proceedings of the 2002 PerMIS Workshop, p201-208, (2002).
• J. R. White, T. Sunagawa, and T. akajima, “Hazardous-duty robots-expeiences and needs”, Proceedings of the IEEE/RSI International Workshop on Inteligent Robots and Systems, p262-267, (1989).
• F. Michaud, M. Arsenault, Y. Bergeron, R. Cadrin, F. Gagnon, M. Legault, M. Millette, and J. Bisson, “Co-design of AZIMUT, A multi-modal robotic platform,”, ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, p801-810, (2003). [https://doi.org/10.1115/DETC2003/CIE-48259]
• S. Srinivasa, D. Ferguson, C. Helfrich, D. Berenson, A. Collet, R. Diankov, G. Gallagher, G. Hollinger, J. Kuffner, and J. Vande Weghe, “A home xploring robotic butler,”, Autonom. Robots, 28(1), p5-20, (2009).
• N. Nilsson, “BA mobile automation: An application of artificial intelligence techniques,”, Proceedings of the International Joint Conference on Artificial Intelligence, p509-520, (1969).
• A. P. Ambler, H. G. Barrow, C. M. Brown, R. M. Burstall, and R. J. Opplestone, “A versatile system for computer-controlled assembly,”, Artificial Intelligence, 6(2), p129-156, (1975). [https://doi.org/10.1016/0004-3702(75)90006-5]
• T. Lozano-Perez, J. Jones, E. Mazer, P. O’Donnell, W. Grimson, P. Tournassoud, A. Lanusse, and B. Handey, “A robot system that recognizes, plans, and manipulates,”, Robotics and Automation, Proceedings IEEE International Conference, 4, p843-849, (1987). [https://doi.org/10.1109/ROBOT.1987.1087847]
• P. Ben-Tzvi, A. A. Goldenberg, and Jean W. Zu, “Design, simulations and optimization of a tracked mobile robot manipulator with locomotion and manipulation capabilities”, Robotics and Automation, IEEE International Conference, p2307-2312, (2008).
• T. K. Kim, H. S. Kim, J. B. Song, J. H. Baek, and J. K. Ryu, “Arm design of a surveillance robot for stable camera view”, Proceedings of the Korean Society of Mechanical Engineers Fall Annual Meeting, p1078-1080, (2010), (in Korean).
• S. S. Kim, J. B. Song, and H. S. Kim, “Design of a manipulator for surveillance robot using CFRP”, Proceedings of the Korean Society for Precision Engineering Spring Conference, p227-228, (2012).
• D. Y. Na, D. M. Choi, H. H. Min, H. P. Moon, J. W. Jung, and Y. T. Kim, “Vision-based docking method for modular robots with 3 DOF docking arm”, Proceedings of Korea Intelligent Information System Society Fall Conference, 19(2), p86-87, (2009).
• Mark W. Spong, and M. Vidyasagar, Robot Dynamics and Control, Canada; John Wiley & Sons Inc, (1989).
• J. J. Slotine, and W. Li, Applied Nonlinear Control, Prentice-Hall, (1991).