Primary energy conversion performance of “Pendulor” wave energy device with bottom gap
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
“Pendulor,” a wave energy device, is the first notable oscillating wave surge converter (OWSC), which consists of a top hinged flap that oscillates in a bounded caisson. From the sea tests conducted by the Muroran Institute of Technology, Japan, it is proven to present 40%–50% energy conversion efficiency. Nevertheless, there are unresolved issues, particularly regarding the physical configurations of the caisson and the flap combination when adopting the OWSC under different sea conditions. The main objective of this research is to investigate the effect of the parametric interactions of caisson configurations on the conversion efficiency. This paper describes the test facility arrangements and the obtained model test results, particularly for the primary energy conversion efficiency of the device for selected configurations. Three-dimensional model tests were conducted in a wave tank to investigate the behavior of a straight caisson configuration using a 1/40th scale following the Froudian scaling for regular waves. Tests were conducted for the conventional caisson arrangement (flap without a gap in the caisson) and for a flap with a bottom gap. The results obtained for the power extraction for different combinations of the damping torque and the wave frequencies were analyzed to compare the power capture for the above caisson configurations. The discovery of the “pumping mode,” which enhances the power capture, is discussed and was verified in this study.
Keywords:
Wave energy, Power capture, Oscillating Wave Surge Converter (OWSC), Bottom gap, Caisson1. Introduction
One of the key challenges currently in the energy sector is to obtain solutions for the new methods adopted for the exploitation of renewable energies. Thus, developing more sustainable techniques for the extraction of power for a circular economy has gained much attention. In this context, solar and wind energies have become advantageous and matured technologies worldwide. However, thus far, wave energy, which is a promising source of indirect form of solar energy, has not yet gained such advantages owing to various reasons. The energy from ocean waves is the most potential form of ocean energy. In which waves are produced by wind action and there is a possibility of converting wave energy into a usable energy. However, over the last four decades, there have not been many commercial applications of wave energy compared to those of other renewables. Major factors for this are the difficulties in its exploitation compared to other renewables such as solar and wind, insufficient resource availability, and few studies in the field.
The Pendulor Wave Energy Converter (WEC) invented by Professor Tomiji Watabe has gained attention owing to its multifunctionality and high efficiency. It has a theoretical efficiency of 100% and a proven conversion efficiency of 40%–50% for the dynamic model established subsequently by him. The system consists of a caisson, with a flap hung down, and a water chamber in the caisson open to the sea. That is facing the offshore open. The flap is driven by the oscillating motion of the standing waves generated in the caisson [1]. The flap is placed at a node point of the waves, and the length of the water chamber in the caisson is selected as 1/4th of the wave length to produce harbor resonance conditions. The latter is necessary to ensure a horizontal water particle motion at the flap. Mostly, the literature is on mathematical models for bottom hinged structures of the Pendulor concept and the Oscillating Wave Surge Converter (OWSC) concept. In regard to the original concept of the Pendulor, the maximum surging effect in a straight caisson is caused by the flap functions at the node point of the standing waves models, which reveals that the caisson parameters significantly affect the device performance. For maximizing the latter, the randomness of the waves also has to be accounted. The objective of this study is to focus partially on experiments for identifying the best configuration to enhance the device performance while optimizing the caisson parametric effect.
A flap-type Pendulor WEC, which is the device under investigation, has the interesting feature of achieving high power conversion efficiency, which was verified in the laboratory as well as by sea trials at the Muroran bay, Japan. The corresponding laboratory experimental results suggested that the primary energy conversion efficiency can reach up to 82% for regular waves [1]-[4]. Mostly, the available analytical and numerical models for characterizing WEC devices are based on two-dimensional (2D) wave tank models, and adopting them to three-dimensional (3D) forms have limitations, particularly when the latter are solved fully analytically. Gunawardana et al. [5] provided the results of a 3D model for a pilot WEC in Sri Lanka using NEMOH. That study estimated the frequency-dependent hydrodynamic coefficients and compared the results with the 2D potential flow theory in terms of the influence of the wave direction and the chamber length of the caisson on the amount of energy captured [5]. Another study by Gunawardana et al. [6] used the WAMIT software tool to analyze the hydrodynamics of four different OWSC concepts. This study presents a notable discovery of a potentially exploitable water chamber pumping mode for a flap in a caisson configuration such that a gap is maintained under the flap. Furthermore, it concludes that obtaining results with linear analysis is a versatile method for understanding the fundamental hydrodynamics of a WEC. However, such analysis is not desirable for the estimation of the potential power capture [6]. The experiments are challenging, similar to the case of modelling. However, in this study, a few experiments were conducted with the aim of verifying the presence of the “pumping mode.” This was subsequently used to estimate the power capture for different flap combinations under different wave conditions.
2. Modelling flap-type WEC with bottom gap
The Pendulor wave energy device can be modelled in the frequency domain using a single degree-of-freedom model. Frequency-domain models have been used extensively to model wave energy converters because they generally provide a clear and concise description of the essential underlying hydrodynamics [7]. Assuming there is no reactive force control, the equation of motion for an OWSC is given by Equation 1.
| (1) |
In Equation 1, ω is the wave frequency, T(ω) is the wave torque on the flap, ζ(ω) is the wave component amplitude, kp flap pitch stiffness, I is the flap moment of inertia about the axis, Ia(ω) is the added moment of inertia, B(ω) is the addeddamping coefficient, Λ(ω) is the power-take-off (PTO) damping coefficient, Θ(ω) is the complex amplitude of the flap rotation, and .
The optimum damping coefficient, Λuc(ω), is given by Equation 2[7].
| (2) |
Following the above, it can be easily shown that the power capture is given by Equation 3[7].
| (3) |
Thus, the calculation of the response of an OWSC and the power capture requires knowledge of the moment of inertia of the flap and the pitch stiffness as well as the frequency-dependent hydrodynamic coefficients of the wave torque, added moment of inertia, and added damping. The normalized power capture is the capture factor, Cf, defined as the ratio of the power capture and the wave power incident on the width of the flap.
| (4) |
where, the incident wave power is given by
| (5) |
where b is the flap width, H is the incident wave height, h is the water height, ω is the wave frequency, and k0 is the wavenumber, which can be calculated from the dispersion relationship given by
| (6) |
The above-mentioned frequency domain models were used to model the OWSC concepts with and without a bottom gap underneath the flap (Figure 1 shows the model boundaries), and some of the important results are highlighted for clarifying this study. Herein, the hydrodynamic coefficients were generated using the potential flow solver, WAMIT [8].
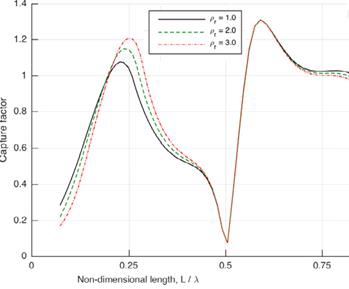
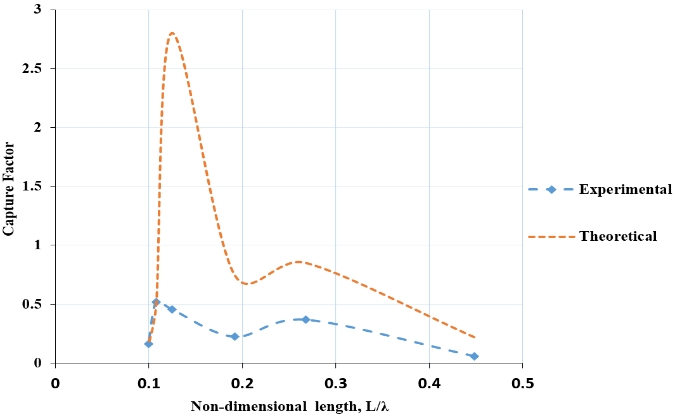
Figure 2 shows the capture factor variation with the nondimensional chamber length, L/λ, for the flap with a bottom gap, where L is the distance between the flap and the back wall of the caisson and λ is the wave length. Figure 3 shows the same for a flap without a gap.
The most striking feature is the peak in the capture factor (see Figure 2) when the chamber length is approximately 1/8 of the wave length, and it is identified as the “pumping mode” of the chamber. In addition, there is also a smaller peak in the capture factor when the chamber length is approximately 1/4th of the wave length and is associated with the resonance of the flap and the water chamber.
The above-mentioned resonance peak in the latter configuration can be notably observed when the flap without a gap, as presented in Figure 3. To investigate the performance of the Pendulor device with a bottom gap, a series of experiments was conducted in different wave tanks using slightly different models. The following sections describe the experimental methodology and the outcomes.
3. Wave tank testing
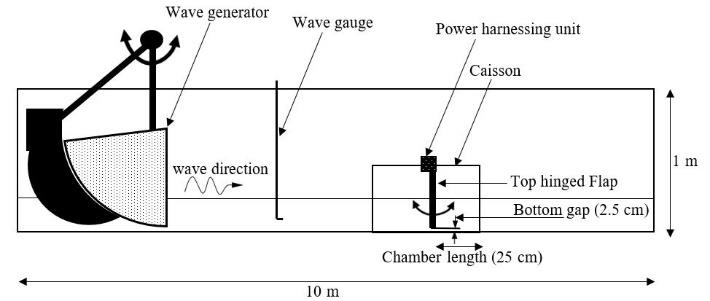
A series of experiments was conducted at the Korean Maritime and Ocean University (KMOU) in Busan, South Korea in a wave flume (7 m × 1 m × 1.7 m), to estimate the energy capture of the device with a bottom gap. The flap was set at 1/8 of the wave length, and the width of the device was set as 1/3 of the width of the wave flume to obtain the 3D wave effect. Experiments were conducted for regular waves, and video footage was also captured to investigate the behavior of the flap under different wave conditions. The wave generation was manipulated by software settings, and the powder brake arrangement was used to load the device as a PTO arrangement. A torque sensor was used to measure the generated torque, and an angle sensor was used to measure the shaft oscillation. More specifically, the flap axis was fixed at the position so that the gap between the flap and the caisson bed was 2.5 cm, and the flap was placed at a distance of 25 cm from the back wall of the caisson. Thus, the flap was at a distance of 1/8 of a wave length of 2 m. Froude scaling of the model was conducted using the Froude number approximated as 6. In addition, experiments were conducted for different wave periods for different damping torques to obtain the power capture.
Another set of experiments was conducted to verify the capture factor variation for the caisson with no gaps in different wave tanks (10 m × 0.5 m × 1 m) at the University of Peradeniya (UOP) Sri Lanka. The flap and the caisson settings were modified using the same scale model (1/40th) while maintaining the 3D environment. The schematic for the experiment at the UOP is shown in Figure 4, and those of the experimental set-ups at both the locations are presented in Figure 5. In the new set-up, the flap could move vertically up or down to change the bottom gap. Thus, the flap was moved downward to set the position of the flap so that there was no gap, to determine the power capture.
4. Results and discussion
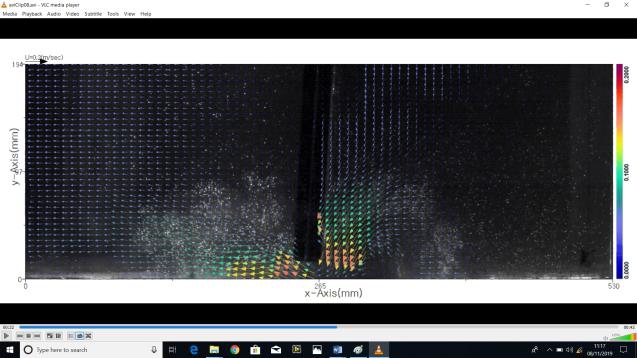
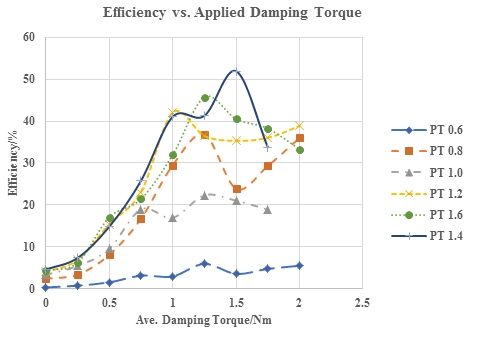
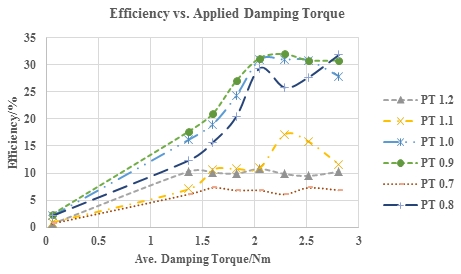
Figure 8 presents the variation in the primary energy capture efficiency (capture factor) with the damping torque for different wave periods (periodic Time) when the flap is located at 1/8th of the wave length from the back wall with a bottom gap. It suggests that the maximum capture factor at 1/8th of the wave length case is approximately 30% higher than that in the case when the flap is at a distance of 1/4th of the wave length. Specifically, this corresponds to the periodic time (PT) 0.8-s curve of Figure 8. These maxima occur in the sloshing or pumping mode, which is described in section 2, when the flap is excited by the incident wave resulting in the formation of a standing wave within the chamber. Figure 9 presents the variation in the primary energy capture efficiency (capture factor) with the damping torques for different wave periods when the flap is located at 1/8 of the wave length from the back wall, which corresponds to the conventional caisson (no gaps) set-up. In addition, the Particle Image Velocimetry (PIV) and video analysis were conducted to validate this pumping mode; however, the detailed discussion of the results and the detailed analysis are not presented herein. The pumping mode was clearly evidenced from the two methods, and below Figures 6 and 7 present the snapshots of the particle dynamics corresponding to 0.8 s and 1.4 s wave periods. In Figure 6, the velocity vectors do not show the additional vibration that corresponds to a chamber length close to 1/4 of the wave length. In contrast, it is easily visible in Figure 7, and the “pumping mode” with the velocity vectors is presented when the wave period is 1.4 s where the chamber length is 1/8 of the wave length.
Figures 10 and 11 qualitatively compare the capture factor variation for a nondimensional length. The setting of the flap For these investigations, the flap was set at a distance of 25 cm from the back wall, which is 1/8 of the wave length with and without a bottom gap in the two different tanks.
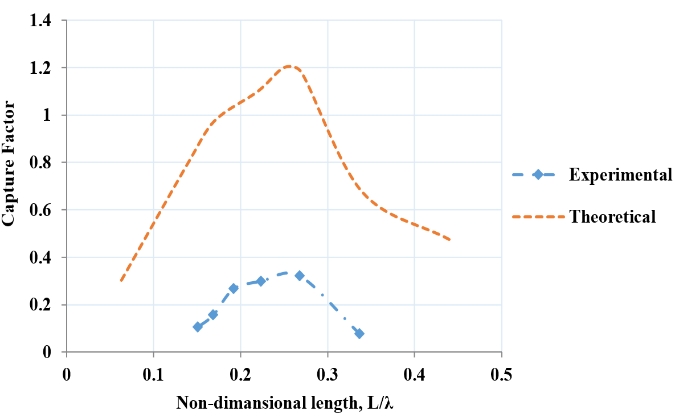
Qualitative comparison of the capture factor for caisson without gap under flap at 1/8 of wave length.
The experimental results shown in Figures 10 and 11 are qualitatively in phase with the analytical results. However, quantitatively, the experimental results are smaller than the expected values. The analytical results were obtained by the linear wave theory, as explained in section 2, and hence, they are typically greater than the real values owing to the numerous assumptions introduced in the analytical model. The experiments were conducted under a restricted environment compared to that in a real scenario, and it is evident that the waves produced in the flume are not always linear. The flume produces second-order stokes waves at lower frequencies, which are not linear, and the time periods concerned in the analysis are actually not the ideal case, as in the analytical case, which is a linear model. The analysis of the wave energy for the nonlinear waves, i.e., cnoidal and second-order stokes waves, does not deviate significantly from the linear analysis. It accounts for approximately ±10% of the linear wave analysis for the wave energy. Although the linear analysis is an ideal tool to understand the fundamental hydrodynamics of a WEC, it is recognized as a poor one for the estimation of the potential power capture [6].
However, the analytical results indicated an approximately 55% increase in the capture factor, whereas the experiments could only achieve approximately 34% increase in the capture when a flap was arranged with the bottom gap. Besides the above-mentioned factors, numerous others could result in such a low level of the quantitative difference, such as the scale effect, unaccounted frictional losses (which can reduce the capture by approximately 10%–20%), possible erroneous estimation of the incoming wave power, and calibration issues. Further analysis of repeated experiments revealed that the calibration of the wave tank with the wave generator required appropriate adjustments. The experimental data accounted for a notable increase in the measurement of the wave height. This fact directly influences the incoming wave power, which leads to reduction in the capture factor, as defined in section 2. However, the experimental and analytical results agreed qualitatively well to conclude that the occurrence of additional resonance, caused by the “pumping mode” in the presence of a bottom gap, enhances the energy capture.
5. Conclusions
In this study, experiments were conducted to verify the analytical model results as well as determine the caisson parametric effect on the conversion efficiency over a long duration. From these efforts, it could be concluded that the results are qualitatively in agreement with the numerical model results as compared to the analytical results. This finding verified the new discovery of the “pumping mode,” which provides the opportunity to harness more energy at a lower chamber length of the device. However, it can be concluded that more realistic and fine adjustments to the test facility and methodologies are needed to verify the accuracy of the experimental results and ensure a numerical validation.
Acknowledgments
This work is related to the research activities undertaken through funding from the grant URG/2017/27/E, University of Peradeniya, Sri Lanka. The extra support given by the “Flow informatics Laboratory” KMOU, South Korea is also highly appreciated.
Author Contributions
Conceptualization, L. U. Bakmeedeniya; Methodology, L. U. Bakmeedeniya and S. D. G. S. P. Gunawardane; Software, L. U. Bakmeedeniyaand B. H. Kim; Formal Analysis, L. U. Bakmeedeniya and S. D. G. S. P. Gunawardane; Investigation, L. U. Bakmeedeniya; Resources, S. D. G. S. P. Gunawardane and Y. H. Lee; Data Curation, L. U. Bakmeedeniya and S.D.G.S.P.gunawardana; Writing—Original Draft Preparation, L. U. Bakmeedeniya; Writing—Review & Editing, S. D. G. S. P. Gunawardane and L. U. Bakmeedeniya; Visualization, L. U. Bakmeedeniya, S. D. G. S. P. Gunawardane and B. H. Kim; Supervision, S. D. G. S. P. Gunawardane; Project Administration, S. D. G. S. P. Gunawardane and Y. H. Lee; Funding Acquisition, L. U. Bakmeedeniya, S. D. G. S. P. Gunawardane, and Y. H. Lee.
References
- T. Watabe, Utilization of the Ocean Wave Energy, Muroran, Japan: Fuji print company Ltd., 2008
- T. Watabe, H. Kondo, H. Shirai, and K. Seino, “Remodelling of Muroran wave test plant,” the Fourth International Offshore and Polar Engineering Conference, pp. 353-358, 1994.
- T. Watabe, H. Yokouchi, H. Kondo, M. Inoya, and M. Kudo, “Installation of the new Pendulor for the 2nd stage sea test,” the 9th International Offshore and Polar engineering Conference, 1999.
-
H. Kondo, T. Watabe, and K. Yano, “Wave power extraction at coastal structure by means of moving body in the chamber,” the 19th International Conference on Coastal Engineering, pp. 2875-2891, 1984.
[https://doi.org/10.9753/icce.v19.192]

- P. Gunawardane, C. Jayan, H. Sanjaya, T. Watabe, and Y. H. Lee, “Modelling of 50 kW top hinged flap type pilot wave energy device for southern coastal region in Sri Lanka,” 2016. Available: https://www.researchgate.net/publication/311230826, .
-
S. D. G. S. P. Gunawardane, M. Folley, and C. J. Kankanamge, “Analysis of the hydrodynamics of four different oscillating wave surge converter concepts,” Renewable Energy, vol. 130, pp. 843-852, 2019.
[https://doi.org/10.1016/j.renene.2018.06.115]

-
M. Alves, “Frequency-domain models,” The numerical Modelling of Wave Energy Converters: State of the Art Techniques for Single Devices and Arrays, Belfast, Northern Island: Academic Press (Elsevier), 2016.
[https://doi.org/10.1016/B978-0-12-803210-7.00002-5]

- WAMIT, WAMIT Inc. – The State of the Art in Wave Interaction Analysis, 2011, http://www.wamit.com, .