Evaluation of the pressure-resistance of the intersection of a Membrane-type primary barrier: part 2 finite element analysis

2.1 Material modeling

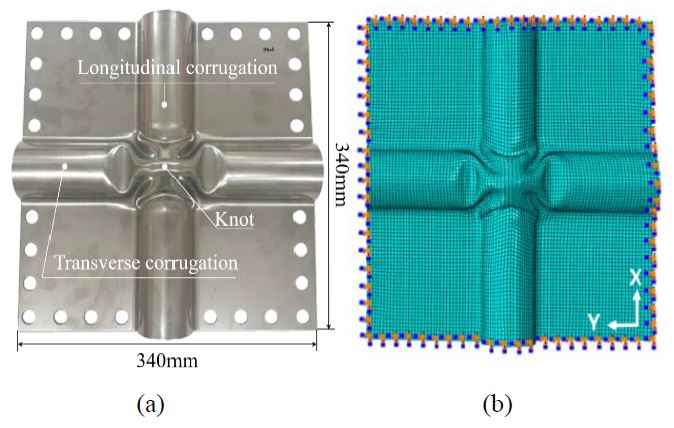
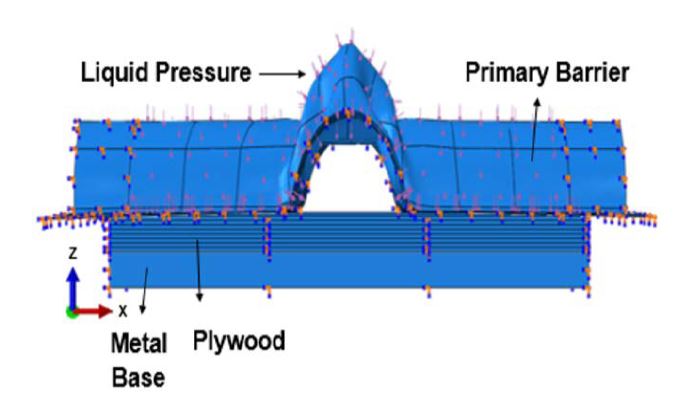
In this study, a membrane-type primary barrier was evaluated using finite element analysis. The test specimen was fabricated using a 1.2 mm thick (T) plate of isotropic cryogenic STS304L with corrugations to avoid thermal shrinkage strain. The specimen dimensions were 340 mm (W) × 340 mm (B). The transverse corrugation (Y) and the longitudinal corrugation (X) intersected each other at a 90°angle; Figure 1 (a) shows a photograph of the test specimen. The geometry of the corrugation intersection was extracted using an optical 3D scanner to model the surface geometry data as shown in Figure 1 (b). The laminated plywood and metal base underneath the primary barrier test specimen were modeled as shown in Figure 2 to replicate the experimental setup.

Figure 1:

Primary barrier specimen: (a) Photograph and (b) finite element model

Figure 2:

Schematic of the finite element model

2.2 Material properties

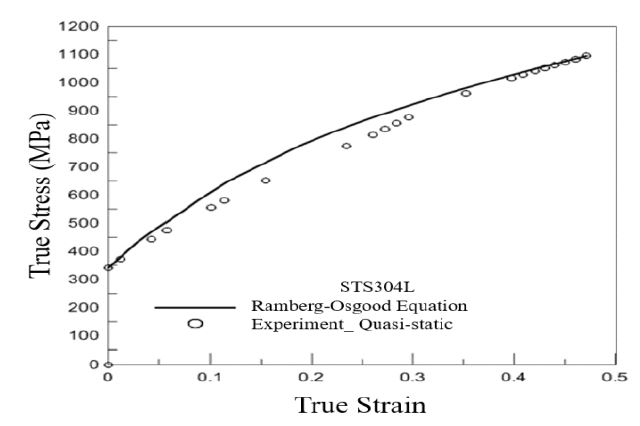
The hydraulic pressure test to simulate the hydrodynamic load in this study was analyzed using the quasi-static tensile profile for STS304L [6]. The Young’s modulus and yield strength were obtained through the 0.2% offset method [7], and Figure 3 shows the obtained elastic region for STS304L.

Figure 3:

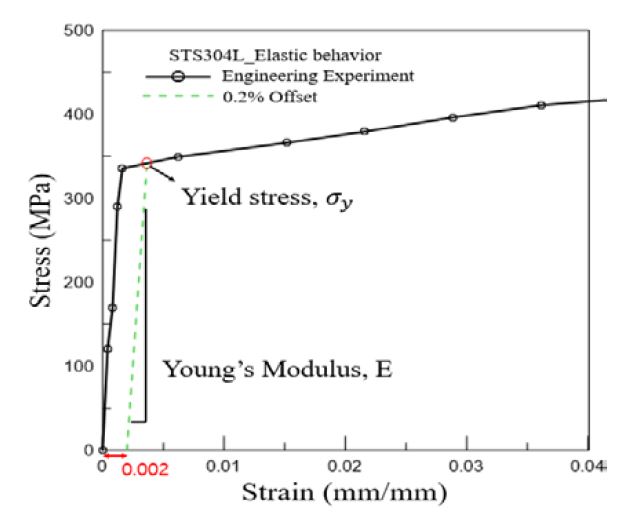
Determination of the elastic region of STS304L from the material stress–strain curve using the 0.2% offset method

The membrane-type primary barrier and steel plate materials were isotropic, whereas the laminated plywood was composed of normal anisotropic materials. The laminated plywood and steel plate did not exhibit notable permanent strain after the hydraulic pressure tests. Table 1 summarizes the physical properties of each material in the elastic region utilized in the finite element analysis.

Table 1:

Mechanical properties in the elastic region for each component

The test specimen experienced permanent strain after the hydraulic pressure tests; hence, its plastic behavior beyond the yield point must be considered. The membrane-type primary barrier was made of ductile STS304L, the plastic behavior of which follows the Ramberg–Osgood Equation [8]. The plastic deformation associated with the Ramberg–Osgood equation is given as follows:

In Equation (1), E is the Young’s modulus of the material, σ₀ is the yield strength, N is the strain hardening, and α is the non-dimensional material constant. Here, the material constant associated with the Ramberg–Osgood equation is given by:

In Equation (3), H and n(1/N) are material constants while ϵ_yp is the constant offset. To estimate the material constants for the test specimen in this study, the stress–strain data from the STS304L quasi-static tensile test were fitted using the Ramberg–Osgood equation, as depicted in Figure 4. Table 2 lists the properties of the primary barrier material.

Figure 4:

Comparison of the theoretical and experimental stress–strain curves

Table 2:

Material properties related to the deformation plasticity

The finite element analysis used the Ramberg–Osgood-equation-based deformation plasticity model for the plastic analysis of ductile metals [8]. The deformation plasticity model employed in the analysis was:

In Equation (4), I is the unit vector and S is the deviator stress expressed as S=σ+pI ; P is the equivalent hydraulic pressure stress given as $$ p=-\frac{1}{3}\sigma :I$$; and q is the von Mises equivalent stress defined as $$ q=\sqrt{\frac{3}{2}S:S}$$. The deformation plasticity model fully simulates the plastic behavior beyond the yield point in the elastic region and iterates until the following condition is satisfied:

2.3 Finite element analysis conditions

The finite element model was designed to correspond to the experimental hydraulic pressure tests used for verification. Loads of 1.8 MPa, 2.2 MPa, and 2.6 MPa were imposed, which corresponded to those applied in the experimental hydraulic pressure test. The magnitude of the pressure was varied to simulate 3 min at maximum pressure and the pressure relief period. Dynamic-implicit finite element analysis was conducted considering the fluid pressure. The contact conditions were chosen based on the layered structure of the hydraulic pressure test equipment. Subsequently, surface-to-surface contact was applied to each material; the friction coefficient between the primary barrier and laminated plywood was set to 0.1 in the finite element analysis [9]. The meshes were discretized using a reduced-integration-type element (eight-node bricks, C3D8R) to overcome the locking effect associated with the intersection geometry. The optimal number of elements was determined based on the grid convergence at the maximum pressure of 2.6 MPa. The primary barrier, laminated plywood, and steel plate featured 10161, 40328, and 15123 elements, respectively, when convergence was achieved, giving a total of 65612 elements. The size of the mesh elements was approximately 0.8 mm. Figure 5 shows the convergence of the displacement as the mesh evolved toward the optimal number of grid elements, and Table 3 lists the conditions used in the present finite element analysis.

Figure 5:

Convergence of the displacement of the finite element model

Table 3:

Finite element analysis conditions

3.1 Validation

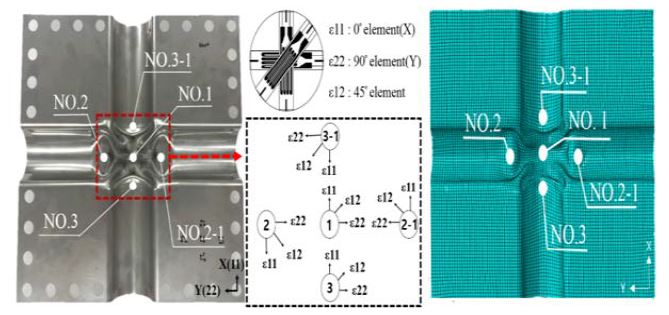
The finite element model formulated in this work was validated against the local principal strain histories obtained from experimental hydraulic pressure tests. The principal strain was measured using a three-axis rosette strain gauge manufactured by Tokyo Measurement Laboratory (TML), and its history was obtained using the principal strain formulae provided by the company [10]. The principal strain history was numerically evaluated at the locations of the strain gauges in the hydraulic pressure test, which are indicated in Figure 6.

Figure 6:

Position of the strain gauges on the primary barrier in the validation experiments

Figure 7 depicts the experimental and numerical time-strain relationships at the primary barrier intersection at different hydraulic pressures. The histories obtained from the finite element analysis and hydraulic pressure test were in good agreement. A minute discrepancy was introduced in the principal strain history due to the initial plastic deformation during the fabrication of the test specimen, which was not accounted for by the model. During the initial plastic deformation, phase transition from austenite to martensite occurs, which causes strain hardening as the yield strength increases [4]. The experimental results verified the suitability of this design support methodology for hydraulic pressure tests.

Figure 7:

Time–strain curves in the hydraulic test and finite element analysis: a) 1.8 MPa b) 2.2 MPa c) 2.6 MPa

3.2 von Mises equivalent stress

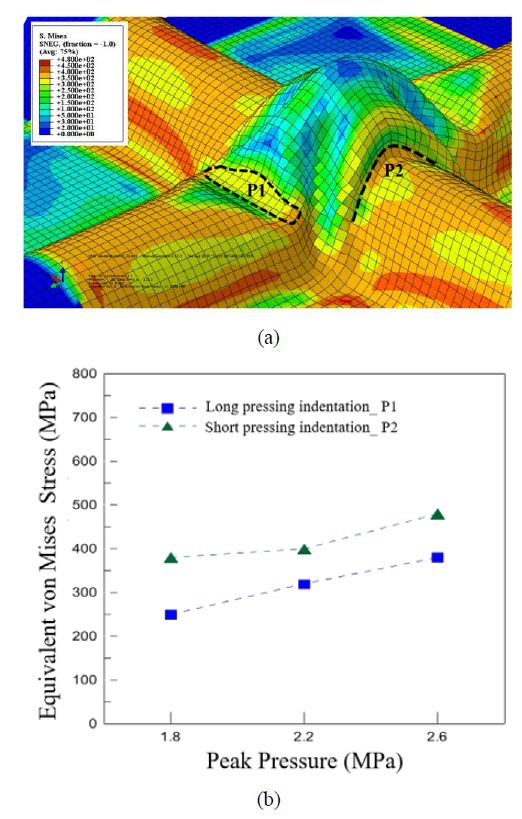
The finite element method was then employed to analyze the von Mises equivalent stress at the corrugation intersection. Figure 8 (a) shows the von Mises equivalent stress distribution at the intersection under the maximum pressure of 2.6 MPa. The von Mises equivalent stress represents the maximum distortion energy at each point of an object subject to a weight. The von Mises yield condition implies that plasticity occurs when the computed equivalent stress becomes greater than the material yield strength, which was 336.91 MPa in this study; it is considered to be the most accurate fault condition. P1 and P2 (Figure 8 (a)) represent the long pressing indentation of the preformed intersection, while P2 represents the short pressing indentation. Figure 8 (b) shows the von Mises equivalent stress as a function of pressure at P1 and P2. As shown in the figure, P2 reaches an equivalent stress greater than the material yield strength at the lowest pressure of 1.8 MPa, and its value is approximately 100% higher than that of P1. In the case of P1, the equivalent stress becomes greater than the material yield strength between 2.2 MPa and 2.6 MPa; thus, plastic deformation would be anticipated to occur between 2.2 MPa and 2.6 MPa according to the von Mises yield condition.

Figure 8:

(a) Von Mises equivalent stress distribution at the maximum pressure of 2.6 MPa calculated by finite element method. (b) Von Mises equivalent stress at P1 and P2 as a function of the peak pressure

3.3 Structural vulnerabilities

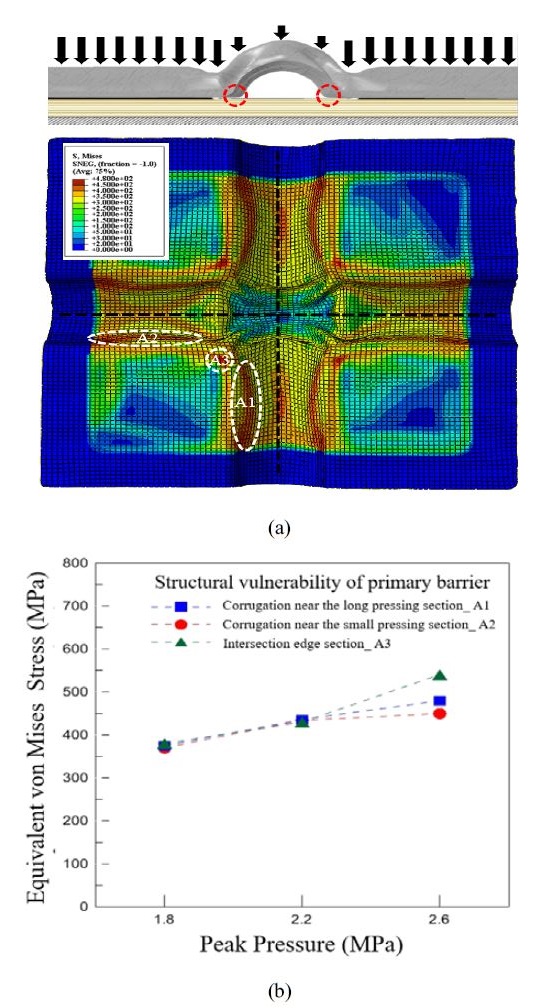
The structural vulnerabilities of the primary barrier were identified under the maximum-pressure environment using the von Mises equivalent stress distribution, and its pressure-resistance capability was evaluated based on these data. Figure 9 (a) depicts the equivalent von Mises stress distribution for the primary barrier test specimen under the maximum pressure of 2.6 MPa. The locations with the maximum equivalent stress values were determined; these structurally vulnerable regions are indicated as A1, A2, and A3 in the figure. A1 represents the structurally vulnerable region of the corrugation near the short pressing indentation, A2 indicates that near the long pressing indentation, and A3 denotes that near the edge of the intersection. Figure 9 (b) shows the von Mises equivalent stress at A1, A2, and A3 with respect to the applied pressure. At the lowest pressure (1.8 MPa), the equivalent stress was similar in all the vulnerable regions and was greater than the material yield strength. Similar increases in all the values were observed at 2.2 MPa. Between 2.2 MPa and 2.6 MPa, however, the equivalent stresses of the three regions began to deviate. In particular, the equivalent stress at A3 increased quickly due to rapid plastic deformation, and its load-bearing capacity was lost. The equivalent stress increase rate was the greatest for A3 and reached its maximum value at 2.6 MPa. The equivalent stress was concentrated at A3, as also demonstrated by the fact that this region of the corrugation intersection sagged under pressure in the experimental hydraulic pressure test. The equivalent stress increase rate at A1 was greater than that at A2, as more plastic deformation occurred at A1 than A2. The long pressing indentation in A2 acts as a support for nearby corrugations, preventing plastic deformation [11].

Figure 9:

Maximum stress on the structurally vulnerable regions of the primary barrier at 2.6 MPa as calculated by the finite element method

3.4 Intersection thickness distribution

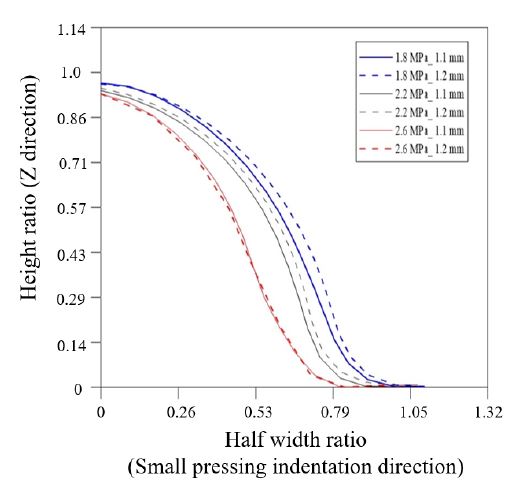
The thickness distribution of the intersection of the membrane-type primary barrier was measured using high-pressure water jet cutting. While the primary barrier sheet was fabricated from a metal sheet with a thickness of 1.2 mm, the intersection thickness distribution varied from 1.1 mm to 1.25 mm, as depicted in Figure 10. The simple bending process during the formation of a membrane-type primary barrier must a ensure uniform thickness with a ±10% tolerance [12]; the observed values were within this tolerance. For increased credibility, an additional finite element analysis was conducted using a model with a minimum thickness of 1.1 mm, and exhibited a corrugation strain history similar to that of the 1.2 mm model, as shown in Figure 11.

Figure 10:

Photograph of the thickness distribution of the primary barrier

Figure 11:

Comparison of the finite element simulations conducted using thicknesses of 1.1 mm and 1.2 mm

Author Contributions

Conceptualization, Y. J. Jeong; methodology, Y. J. Jeong and H. T. Kim; Software, Y. J. Jeong; Formal Analysis, Y. J. Jeong; Investigation, Y. J. Jeong and H. T. Kim; Resources, Y. J. Jeong; Data curation; Y. J. Jeong; Writing-Original Draft Preparation, Y. J. Jeong; Writing-Review & Editing, J. D. Kim and S. G Kim; Visualization, Y. J. Jeong; Supervision, M. S. Kim and S. K. Kim; Project Administration, J. M. Lee; Funding Acquisition, All Authors.