Parameter study of lithophane for efficient reproduction of 2D image as 3D object using 3D printing

1. Introduction

Lithophane is a very thin translucent porcelain that can only be seen clearly when it is backlit using a light source. It was originally an art piece carved using warm wax on a glass plate. However, the development of various modern processing technologies has made it possible to manufacture lithophane using computerized numerical control machines (CNC machines) or 3D printers [1]-[5].

3D printing technology, also known as additive manufacturing (AM), involves using a 3D printer to layer raw materials to create 3D objects. It is used for prototyping in the aviation/automotive industry. It receives remarkable attention, because it enables rapid prototyping; furthermore, it offers an easy and clean way to produce complex shapes [6]. In addition, because related original patent rights on 3D printing technology have expired, it has been fused with IT technology to create more varied applications. One of such applications is the lithophane printing technology that can convert 2D images to 3D objects using plastic, instead of wax, similar to the original production of lithophane porcelain [7][8].

Lithophane printing technology produces plates of photos of landscapes or people with a quality similar to a photograph using various 3D printers with high resolution (approximately one-fifth of the width of the human hair) [8].

We studied the optimal parameter values of lithophane output using a human photo, because it is more easily identifiable by the eyes, compared to landscape pictures. Among all the parameters of lithophane, the three that most significantly affect the quality of the 3D object were considered: (1) Vector per pixels: 4, 5, and 6; (2)Thickness of the 3D object: 2 mm, 2.5 mm, 3 mm, and 4 mm; and (3) Width of the thinnest layer: 0.5 mm and 1 mm. These parameters, in addition to the fabrication time, were investigated to determine the optimal parameter values for producing a clear 3D object.

To analyze the effectiveness of the parameter study, the fabricated 3D object was reconverted to 2D image using a camera. Then, the Matlab histogram was used to measure the standard deviation of the three parameters. In this case, the X-axis represented the degree of lightness and darkness from 0 to 225, and the Y-axis represented the number of pixels of the contrast equal to the value of X. We determined from the shape of the output whether the Y values tilted to the left or right of the center of the X-axis (approximately 128). Then, we studied the optimal values in comparison to all the parameter values.

2. Image selection and Conversion from 2D to 3D

As above-mentioned, lithophane printing technology reproduces the 2D images of plates with quality similar to that of a photo using various 3D printers with high resolution (approximately one-fifth of the width of the human hair). In this study, the 2D image converted to a 3D object was the picture of a person, because it is easily distinguishable by the eyes, compared to that of a complex landscape. To minimize the effect of the three parameters on the output quality and on the analysis of the number of black and white pixels of the reconverted 2D image, we did not edit the picture. The picture used in the study is shown in Figure 1.

Figure 1:

Original image

To apply the lithophane printing technology to the 2D image shown in Figure 1, it is necessary to convert the file extension from 2D image to 3D object (from JPG to STL). Among the parameters of the lithophane technology that most significantly affect the quality of 3D objects, we considered three; a total of 24 converted files were generated. The parameters were as follows: (1) Vector per pixels: 4, 5, and 6; (2)Thickness of 3D object: 2 mm, 2.5 mm, 3 mm, and 4mm; and (3) Width of the thinnest layer: 0.5 mm and 1mm. The STL file conversion program used was the 3dp.rocks program.

2.1 Vector per pixel

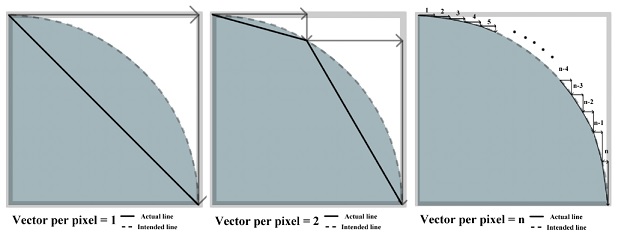
In the model settings of this program, the vector per pixels refers to the number of vectors in one pixel. As the number of the vectors of each pixel of the 2D image to be represented as a 3D object increases, the number of diagonals that follow between the vectors increases, and the rounded surface of the object becomes smooth. This is represented in detail in Figure 2. When the 3D object has three or less vectors per pixel, following conversion, it is expressed as a minute angular portion, and looks more like a drawing than a photo. Even if we had continued to increase the number of the vector per pixel to make the surface smoother, the STL-converted file restricts the maximum number of vectors to six; therefore, we considered only three values, 4, 5, and 6.

Figure 2:

Vector per pixel

2.2 Thickness and thinnest layer

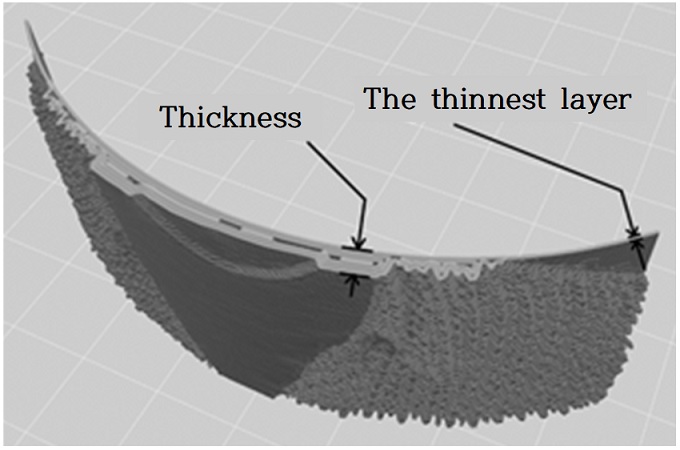
The thinnest layer and the thickness of the program’s model settings refer to the thinnest layer and the thickest thickness of the surface of the 3D object, respectively. When the 3D object is illuminated using a backlight, the thinner the surface of the object is, the brighter the thicker part of the surface. The object looks like a black-and-white version of the original picture, acting as contrast. The thinnest layer should be very thin, and the surface of the 3D object should be very thick, for the contrast of the image to be clearly expressed. If, during the conversion of the STL file, the width of the thinnest layer is set to less than 0.5 mm, the 3D object cannot be manufactured, because it is not partially expressed in a slicing program before production. Furthermore, if the width of the thinnest layer, following conversion, is 1 mm or more, it becomes difficult to transmit the backlight; thus, 1 mm or less is ideal. Considering that the thickness of the extruded filament of the 3D printer used in the manufacturing process was 0.4 mm ~ 0.5 mm, the thinnest layer value was set to 0.5 mm and 1 mm. If the thickness value following conversion was 2 mm or less, the light gray surface will be absent, making it difficult to represent the detailed appearance. If it is converted to a surface that is thicker than 6 mm, it is represented in the conversion program. However, when the lithophane to be manufactured without support is presented with the thick part in the air, the shape will flow out. Therefore, we will convert the STL file to a 3D object with thickness not exceeding 6 mm. Figure 3 shows the width of the thinnest layer and the thickness values in the conversion program.

Figure 3:

Thickness and thinnest layer in the conversion program

3. Manufacturing process and Result

Although there are other parameters corresponding to the three specified parameters affecting the output, varying them results in very slight changes in the appearance when the light is on. Such outputs are considered in addition to the printing time, and are considered in the final analysis. The printing time with each parameter depends on the width of the thinnest layer and the thickness of the lithophane; furthermore, the larger the vector per pixel, the longer printing takes. The various printing times are shown in Table 1. When studying the optimal quality, it is necessary to consider the printing time in addition to the parameter analysis, because an output that takes a relatively long time to print is considerably inefficient, and cannot be regarded as the lithophane with the optimal parameters. Based on all the variations of the three parameters and the printing time, there were ten lithophanes in this study. These parameter values are shown in Table 2, and the resulting STL file is summarized in Table 3.

Table 1:

Printing time according to each parameter: (A) Thickness, (B) Width of the thinnest layer, (C) Vector per pixel

Table 2:

Parameters of the 10 outputs

Table 3:

The 10 STL files

The converted STL files were manufactured using a 3D printer (GIANTBOT G5 Plus). They were manufactured based on the same basic settings, to ensure that the settings of the 3D printer did not affect the output quality. The output of the 3D objects is shown in Figure 4 (a), and the backlit view is shown in Figure 4 (b).

Figure 4:

Output of 3D objects: (a) Light off, (b) Light on

4. Reconversion from 3D object to 2D image

As shown in Figure 4 (b), the 3D objects fabricated from the STL file are reconverted to 2D images using the backlight. Prior to this, we used sandpaper to remove the unnecessary parts of the output, and smoothen the surface for precise measurement. Then, the output was transmitted through a backlight at a constant distance. The 3D surface of the thinnest layer that transmits light was the brightest, and that of the thickest layer was the darkest. The 3D object was reconverted to a 2D image similar to a black-and-white version of the original picture by representing the contrast according to its differences. In the reconverted 2D image, the color of light was converted into black and white (color to zero), and the black and white pixels were counted using the Matlab program. The reconverted 2D image is shown in Table 4.

Table 4:

Reproduced Black and white 2D image

5. Analysis of 2D image using Matlab

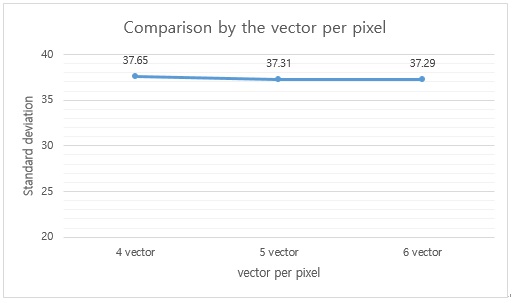
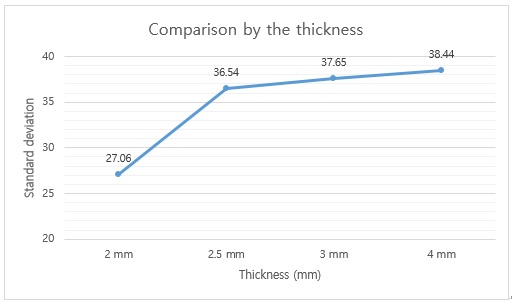
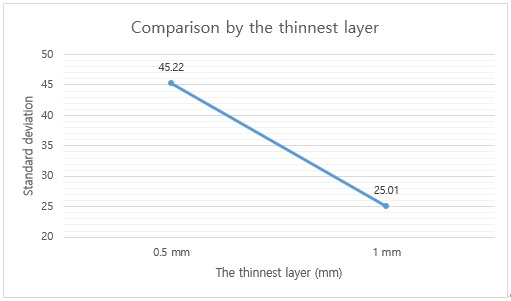
If a light source whose temperature rises during light emission is used, lithophane made of polylactic (PLA) material may melt or burn due to the high temperature. Therefore, we used a small flashlight that did not generate heat as the light source. We made a case with which we attached the flashlight at a certain distance to the back of the lithophane for each parameter, and set the flashlight to apply the same amount of light. However, when analyzing the 2D image using Matlab, even when the light source changed, the shade of the lithophane was consistent with the properties of the surface of the lithophane. The reconverted 2D image was measured based on the number of the black and white pixels of the entire surface using Matlab. The standard deviation of each pixel was analyzed using the histogram of the Matlab. Furthermore, the 2D image was analyzed, using the Matlab’s function code to obtain the histogram of the image and analyze its standard deviation. First, the reconverted 2D image (jpg file) was loaded, using Matlab’s ‘imread()’ function. Then, a function called ‘imhist()’ was used to display the histogram of the image in the Matlab program. The histogram is a graph that shows the distribution of the brightness and darkness values of the 2D image, making it possible to confirm the difference between the composition of the brightness and the contrast. The X-axis of the histogram is a value obtained by digitizing the brightness on a scale of 0 to 255, and the Y-axis is the number of pixels corresponding to the contrast of the X-axis. The images biased to the left and right of the X-axis center (127.5) were a relatively dark 2D image and a relatively bright 2D image, respectively. First, the standard deviation, according to the vector per pixel, was analyzed. Although changes in the vector per pixel corresponded to slight changes in the standard deviation, the difference was minimal, compared to other parameters. Then, the standard deviation according to the thickness of the lithophane and the width of the thinnest layer were compared. The thicker the thickness, the larger the standard deviation value. As the standard deviation increased, each pixel distribution became wider, as a result of which various contrasts could be expressed. The thinner the thinnest layer, the larger the standard deviation value. Therefore, the difference between both was directly proportional to the clarity of the image. The histogram analysis of each parameter’s variations is shown in Figure 5, Figure 6, and Figure 7, respectively.

Figure 5:

Standard deviation of histogram according to vector per pixel

Figure 6:

Standard deviation of histogram according to the thickness

Figure 7:

Standard deviation of histogram according to the width of the thinnest layer

6. Conclusion

Based on the variations of the selected three parameters and the 3D printing time, a 3D object was fabricated from the original 2D image. The relationship between the parameters and the printing time was less significant when the values of the width of the thinnest layer, thickness, and vector per pixel value were larger. By analyzing the number of pixels of the histogram, the reconverted 2D image and 3D object were compared, and the following observations were made: (1) The amount of time taken to fabricate the 3D object and the clarity of the object were not proportional. (2) The vector per pixel had little effect on the standard deviation of the reconverted 2D image. (3) The difference between the overall thickness and thinnest layer had a significant effect on the standard deviation of the reconverted 2D image. In conclusion, when the light was on, the clarity of the 3D object was affected by the thickness.

However, the limitation of this study is that it took only three parameters into consideration; the experiment results were obtained by specifying only the parameters related to the surface of lithophane. Furthermore, the light source we used to invert the 2D image is a commonly available lamp. Depending on the shape of the light source, the amount of light may not evenly illuminate the surface. Therefore, the edges of the pictures in Table 4 are relatively dark, and the center is relatively bright. Because we compared the surfaces of ten images, the other parameters were fixed. However, varying other parameters, such as the light source, could have yielded more results.

Acknowledgments

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education and Ministry of Science (2019R1G1A1009980). This paper is an extension of the 2nd International Conference on Advanced Convergence Engineering (ICACE2019).

References

• M. Carney, “Lithophanes… not a dead art form,” Ceramics Art and Perception, no. 87, pp. 24-29, 2012.
• J. Weiler, P. Fernando, T. Ingalls, and S. Kuznetsov, “Lithobox: Creative practice at the intersection of craft and technology,” Proceedings of the Thirteenth International Conference on Tangible, Embedded, and Embodied Interaction, ACM, pp. 471-477, 2019. [https://doi.org/10.1145/3294109.3301258]
• C. M. Mullin, “Frame for displaying lithophanes using natural daylight or integrated lighting system,” U.S. Patent Application 0016092, Jan.15, 2015.
• J. Dufort, “Lithophane-like article and method of manufacture,” European Patent Application 1318003, Nov. 23, 2003.
• J. Dufort, “Lithophane-like article and method of manufacture,” World Intellectual Property Organization 079451, Sep. 16, 2004.
• T. Cavanaugh and N. Eastham, “The 3D printer as assistive technology,” Association for the Advancement of Computing in Education (AACE), DAAAM International Scientific Book, pp. 95-102, 2017.
• M. Yuan and D. Bourell, “Fundamental issues for additive manufacturing of lithophanes,” International Conference of Advanced Research in Virtual and Rapid Prototyping, CRC Press, pp. 89-93, 2013.
• H. Brooks, M. Lupeanu, and T. Abram, “Production of personalized lithophane lighting products using AM,” DAAAM International Scientific Book, vol. 11, 2012.