해상 부유 쓰레기 수거를 위한 무인 스키머 로봇의 경로 추종 제어 시스템 설계
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
최근 해상 부유 쓰레기로 인한 해양 환경오염은 전 세계적으로 심각한 문제로 대두되고 있으며, 이를 위한 하나의 대안으로 무인 스키머 로봇을 활용한 쓰레기 수거 시스템을 고려할 수 있다. 본 논문은 스키머 로봇의 자동적 쓰레기 수거 작업을 위한 중요한 기능 중 하나인 경로 추종 제어 시스템의 설계 방법을 제안한다. 제안된 제어 시스템은 스키머 로봇의 속도 제어를 위한 내부 루프와 경로 추종 제어를 위한 외부 루프로 구성된다. 속도 제어 시스템은 로봇에 탑재된 두 대의 추진기를 제어하면서 스키머 로봇의 선속도 및 각속도의 제어를 수행하는데, 이를 위해 안티와인드업(anti-windup) PI 제어기가 설계된다. 또한 스키머 로봇의 정교한 경로 추종 제어를 위해, 견시거리 및 선속도 참조값을 자동적으로 조정하며 경로를 추종하는 개선된 퓨어퍼슈트(pure pursuit) 알고리즘이 설계된다. 제안된 기법은 속도제어, 제어파라미터, 경로추종의 관점에서 수행된 몇몇의 시뮬레이션을 통해 평가된다.
Abstract
Recently, marine pollution caused by floating trash has been considered a serious environmental problem globally. To overcome this problem, a trash collection and treatment system using unmanned skimmer robots can be considered. In this study, a method of designing a path-tracking control system, which is essential for automatic trash collection by using skimmer robots, was developed. The proposed control system comprises an inner loop for the speed control of the skimmer robot and an outer loop for path-tracking control. The speed control system controls the linear and angular velocities of the skimmer robot by controlling two different propellers, and two anti-windup PI controllers were designed for this purpose. For the sophisticated path-tracking control of the skimmer robot, an improved pure pursuit algorithm was designed to adjust the look-ahead distance and linear velocity reference automatically. The proposed method was evaluated through several simulations considering the velocity and other control parameters, as well as the path-tracking performance.
Keywords:
Unmanned skimmer robot, Path tracking control, Pure pursuit algorithm, Trash collection system키워드:
무인 스키머로봇, 경로추종제어, 퓨어퍼슈트알고리즘, 쓰레기수거시스템1. 서 론
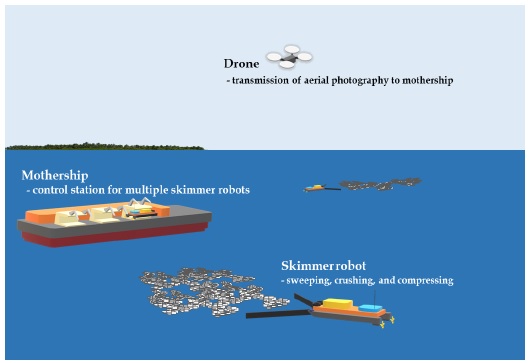
해상은 선박 사고로 인한 유류 유출, 무분별한 쓰레기 투척 등 다양한 잠재 요인에 노출되어 있다. 특히 최근에는 쓰나미 등 자연 재해 혹은 무분별 투척으로 인해 바다로 흘러 모인 플라스틱 등의 부유 쓰레기들이 특정 해역에 모여 거대 쓰레기섬을 형성하는 등 심각한 해양 환경오염 문제를 야기하고 있다[1]. 해상 부유 쓰레기 문제의 처리에 대한 하나의 방안으로 Figure 1과 같은 해상 쓰레기 수거/처리 시스템을 고려해 볼 수 있다. 이 시스템은 크게 항공관측 드론(drone), 방제모선(mothership), 스키머 로봇(skimmer robot)의 3가지 시스템으로 구성된다. 항공관측 드론은 전역위치인식을 기반으로 해상 부유 쓰레기 영역의 관측영상을 촬영하여 모선으로 전송하는 역할을 담당한다. 방제모선은 항공관측 드론과 격납 가능한 다수의 스키머 로봇을 보유하며, 이들의 통합 제어 및 모니터링을 위한 관제 시스템이 탑재되며, 스키머 로봇들이 수거해온 쓰레기를 한데 모아 처리하는 역할을 담당한다. 스키머 로봇은 방제모선과 네트워크로 연동되어 있으며 모선으로부터 실시간 제어 명령을 전송받아 해상에 널려있는 부유 쓰레기를 수거하여 모선에 적재하는 역할을 담당한다. 본 논문은 Figure 1의 해상 쓰레기 수거/처리 시스템을 구성하는 핵심장비중의 하나인 스키머 로봇의 필수적인 기능이라 할 수 있는 경로 추종 제어(path tracking control)를 위한 방법론을 다루고자 한다.
선박의 경로 추종 제어 기법에 관한 연구는 오랫동안 지속되어 왔으며, 대형 선박에 이용되는 경로 추종 제어 시스템은 정속으로 항해 중인 상태에서 경로 추종을 위한 조타각의 제어입력을 산출하는 것이 일반적이다. 이는 속도를 자유롭게 변경시키는 것이 선박의 주기관에 무리를 줄 수 있고 속도 변경 시 선박의 동적 거동에 따른 안정성에 영향을 미치기 때문이다.
스키머 로봇은 상대적으로 작은 규모의 선박이라 할 수 있는데, 쓰레기 수거 기능을 구현하기 위해서는 보다 신속하고 정교한 모션의 구현이 가능해야 한다. 사실상 신속하고 정교한 경로 추종 제어 기법은 지상에서 활용되는 이동로봇 분야에서 활발히 연구되고 있다. 이동로봇을 대상으로 하는 경로 추종 제어기법은 다양하게 존재한다. 대표적으로 이동할 경로를 연속함수로 근사하여 로봇을 접근 시키는 방법[2], 이동 경로를 점들의 시퀀스로 간주하여 로봇이 목표점을 따라 추종시키는 PTP(point-to-point)제어방법 등이 있다. 한편 퓨어퍼슈트(PP:pure pursuit) 기법은 일정 거리를 앞선 목표점을 설정하고 이를 추종토록 로봇을 제어하는 기법으로 구현이 쉽고 성능 또한 우수하여 널리 이용되는 방법이다[3]. 하지만 이 기법은 로봇을 목표점에 수렴시키기 위한 선회 조향각의 해법만을 제시하기 때문에 정교한 모션을 구현하기에는 한계가 있다.
본 논문에서는 스키머 로봇의 역할이 해상 부유 쓰레기 수거라는 점을 고려하여 저속에서도 제어가 용이하도록 두 개의 추진 장치로 구성된 스키머 로봇의 수학적 모델을 구한다. 경로 추종 제어시스템은 안티와인드업 PI제어(anti-windup proportional-integral control)에 기반한 속도제어 루프와 개선된 퓨어퍼슈트 경로추종 루프로 구성된 제어 시스템을 제안한다. 특히 로봇의 각속도 제어와 함께 가속/등속/감속의 선속도 제어, 경로 수렴속도 및 오버슈트 조정을 일괄적으로 수행할 수 있는 개선된 PP알고리즘을 제안한다. 제안된 방법은 스키머 로봇의 수학적 모델을 기반으로 경로추종제어에 관한 시뮬레이션을 통해 평가된다.
2. 로봇 모델링 및 속도 제어기 설계
2.1 2차원 선박 모델
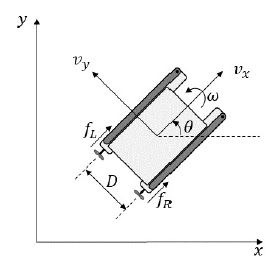
본 논문에서 다루는 스키머 로봇의 모델은 이차원 평면상에서 서지-스웨이-요(surge-sway-yaw)모션을 가지는 선박 모델로부터 유도된다[4]. Figure 2는 x-y 평면상에 정의된 스키머 로봇의 기구학적 모델을 나타낸 것이다. 여기서 υx, υy는 로봇 물체좌표계를 기준으로 x축, y축 방향에 대한 선속도를 나타내며 w는 요축에 대한 각속도를 나타낸다. 또한 fL, fR은 프로펠러에 의해 발생되는 추력을 각각 나타내며 D는 프로펠러 구동축 간의 거리를 나타낸다.
Figure 2에 나타난 바와 같이, 스키머 로봇의 물체좌표계에 대한 선속도와 각속도 벡터 (υx,υy,ω)⊤는 식 (1) ~ 식 (3)을 통해 전역 좌표계를 기준으로 하는 선속도와 각속도 벡터 로 변환될 수 있다. 또한 식 (1) ~ 식 (3)의 미분방정식에 대한 해를 통해 전역 좌표계상의 로봇의 위치 및 방향 벡터 (x,y,θ)⊤를 산출할 수 있다[4].
| (1) |
| (2) |
| (3) |
스키머 로봇의 동적 모델은 선박의 6자유도 운동 모델로부터 유도할 수 있으며, 본 논문에서는 문헌[5]를 참고하여 식 (4) ~ 식 (6)과 같은 간략화 모델을 이용한다.
| (4) |
| (5) |
| (6) |
여기서 m11, m22, m33은 각 축 방향에 대한 질량 및 관성모멘트 항을 나타내며, 이들 항들은 각각 부가질량을 포함한다. d1, d2, d3는 각각 서지, 스웨이, 롤 방향에 대한 유체동력학적 감쇠계수(hydrodynamic damping coefficients)를 나타내며 지수상수 α1, α2, α3와 함께 지수함수로 모델링된다(각각의 파라미터에 관한 세부 설명은 문헌[5] 참조). 이때 sgn(ㆍ)와 |ㆍ|은 각각 부호함수(sign function) 및 절대값을 나타낸다. 물체좌표 중심에서의 힘(f)과 모멘트(T) 좌우 추진기로부터 발생되는 힘 (fL,fR)⊤으로부터 식 (7), 식 (8)의 관계를 통해 구할 수 있다.
| (7) |
| (8) |
2.2 추진기 모델
본 논문에서는 스키머 로봇이 두 대의 추진기를 가지는 것으로 가정하여 식 (9)의 모델로 표현한다. u는 추진기를 구동시키기 위한 입력변수로 [-100,100]의 범위를 가지며 단위는 [%]이다.
| (9) |
여기서 umax는 출력을 포화시키기 위한 임계치를 나타내며 100의 값으로 설정된다. 또한 umin은 불감대 영역에 대한 임계치를 설정하기 위한 상수이다. 본 논문에서는 umin을 5로 설정함으로써 전체 입력 구간 중 -5∼5%의 불감대를 형성토록 설정한다. K는 비례상수로 100으로 설정하여 100% 입력에 대해 추진기를 통해 발생하는 추진 힘은 10kN이라고 가정한다. 식 (9)의 추진기는 0 ~ ±100으로 정규화된 제어입력에 대하여 프로펠러를 구동하며 이를 통해 얻어지는 추진 힘에 대한 관계를 나타내며, 포화기를 통해 출력 제한 및 비선형성의 부여를 위한 불감대가 포함된 근사모델이다(Figure 5 참조).
2.3 속도 제어 시스템
본 논문에서 스키머 로봇은 기본적으로 속도 제어를 통해 모션의 제어가 가능하도록 시스템을 구성한다. 즉 스키머 로봇은 원하는 선속도(υref)와 각속도(wref)에 대한 설정값(reference)을 참조하여 좌우에 장착된 두 개의 추진기를 구동하는 피드백 제어(feedback control)를 수행한다. 본 논문에서는 이를 위한 제어기로 간단한 PI 제어기를 설계한다. 일단 스키머 로봇의 원하는 선속도와 각속도 벡터가 (υref,wref)⊤가 설정되면, 식 (10)에 의해 좌우 속도 참조값으로 변환된다.
| (10) |
또한 현재 로봇의 좌·우측 추진기를 구동하게 되면 로봇의 속도(υ)와 각속도(ω)에 영향을 미치게 되는데, 식 (10)을 이용하면 (υL,υR)⊤을 산출할 수 있다. 왼쪽 추진기에 대한 오차를 eL(t)라 할 때 eL(t)=υLref(t)-υL(t)라 할 수 있다. 따라서 추진기의 구동 제어는 속도 참조값과 현재의 속도에 대한 오차 eL(t)의 감쇄를 목표로 하고, 이를 위해 식 (11)의 PI제어기를 구성하여 추진기를 구동하기 위한 제어입력을 계산한다.
| (11) |
여기서 P(t)는 비례항을 나타내며 비례게인(proportional gain) Kp를 적용하여 P(t)=KpeL(t)의 비례제어 입력값이 산출된다. 이때 적분항 I(t)는 안티와인드업(anti-windup) 기법을 적용하여 식 (12)와 같이 산출된다.
| (12) |
여기서 Ki, Kaw는 각각 적분게인 및 안티와인드업 게인이다. 실제 추진기의 제어입력은 식 (11)의 ξ(t)에 포화함수(saturation function)를 거친 정제된 값 u(t)=sat(ξ(t))을 이용한다. 오른쪽 추진기에 대한 제어기는 앞서 설명한 제어기에 eR(t)=υRref(t)-υR(t)를 적용하여 동일한 구조로 구성된다.
3. 경로 추종 제어 알고리즘
본 논문에서는 해상에 널려있는 부유 쓰레기들에 대한 좌표정보가 드론에 의한 실시간 항공사진으로부터 획득되어 쓰레기 영역 분할(region segmentation) 및 공간 매핑 기법으로 이미 해상쓰레기 지도가 작성되어 있다고 가정한다. 해상쓰레기 지도가 주어지면, 그 다음단계로 쓰레기 수거를 위한 경로계획이 수행된다. 일반적으로 청소로봇, 탐사로봇 등의 경우에는 정해진 범위를 모두 경유토록 하는 경로계획법이 필요한데, 이러한 기법을 전범위 경로계획법(coverage path planning)이라 한다. 전 범위 경로계획법에도 여러 가지 기법들이 존재하나, 본 논문에서는 지그재그(zigzag)탐색 기법을 적용한다[6]. 경로계획 알고리즘의 역할은 해상쓰레기 지도를 입력받으면 스키머 로봇의 쓰레기 수거용량을 고려하여 영역을 분할하고, 분할된 영역마다 지그재그 형태로 모든 영역을 탐색하기 위한 경유점들의 집합을 출력한다. 앞서 언급한 사항을 본 논문에서 모두 다루는 것은 지면의 한계가 있으므로 본 논문에서는 경로가 이미 계획되어 경유점의 집합이 주어졌다고 가정한다.
3.1 퓨어퍼슈트(Pure pursuit) 추종 제어 알고리즘
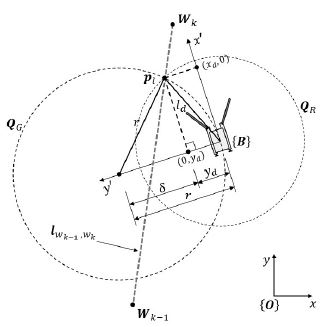
본 논문에서 경로 추종 제어 시스템은 퓨어퍼슈트(PP)알고리즘을 기반으로 구현된다. PP 기법의 원리를 간략히 설명하면 다음과 같다. 우선 현재 추종하고자 하는 경유점(waypoint)을 Wk라 하고 이전 단계의 경유점을 Wk-1이라 하자(Figure 3 참조). 그러면 두 개의 경유점 {Wk-1,Wk}을 통과하는 직선(lWk-1,Wk)을 추출할 수 있다. 또한 현재 로봇의 위치에서 반경 ld를 가지는 원 QR을 고려하면 QR과 직선 lWk-1,Wk의 교점(intersections)이 추출된다. 교점이 존재하는 일반적인 상황에서 로봇 전방부에 위치한 전역좌표계 상의 pl을 고려하자. 이제 pl을 로봇의 몸체좌표계 {B}를 기준으로 좌표변환을 수행하여 (xd,yd)로 변환되었다고 하자. 또 교점 pl을 지나면서 로봇의 몸체좌표계의 y′축 위에 원점이 위치하는 원 QG를 고려할 수 있는데, 이 원의 반지름을 r이라 하자. 본 논문에서는 반지름 r위를 로봇이 선회하도록 제어할 것이므로 r을 선회반경이라 명명한다. 앞서 설명한 조건으로부터 식 (13) ~ 식 (15)의 제약 조건식을 유도할 수 있다.
| (13) |
| (14) |
| (15) |
식 (13) ~ 식 (15)에 대한 연립방정식에 미지수 δ를 소거하면서 연립방정식을 풀면 선회반경 r에 대한 간략화 식을 식 (16)과 같이 유도할 수 있다.
| (16) |
즉 스키머 로봇의 선회반경은 로봇의 몸체좌표계상의 pl에 대하여 거리 ld와 y축 좌표 값인 yd를 알면 식 (16)의 간단한 계산으로 쉽게 산출가능하다. 본 논문에서는 ld를 견시거리(look-ahead distance)라 명명한다. 일반적으로 견시거리값이 크면 경유점 경로 상에 진입이 느리며, 반대로 너무 작은 경우 진입 시 불안정한 움직임을 초래한다. 따라서 적절한 값의 선택이 필요한데 이에 관해서는 3.2절에서 다시 다룬다.
PP 알고리즘을 구현하는 과정에서 우선적으로 고려해야 할 사항은 주어진 경로 상에 견시점을 설정하는 것이다. 기하학적으로 볼 때, 이는 로봇의 위치를 원점으로 하는 원 QR과 두 경유점을 통과하는 직선 lWk-1,Wk 와의 교점을 구하는 것이다. 이를 위해 다양한 방법이 존재하겠으나 본 논문에서는 원과 직선을 각각 QR∈R3×3, lWk-1,Wk∈R3로 표현하고 교점을 추출하는 기법을 이용한다[7]. 또한 두 개의 교점이 존재하는 경우에는 스키머 로봇의 진행 방향에 놓인 교점을 선택하는 전략을 적용하며, 이는 벡터 내적의 성질을 이용하여 쉽게 구현 가능하다. 본 논문에서는 스키머 로봇의 속도 및 각속도를 통해 로봇의 모션을 제어한다. 원의 경우 원주를 따라 운동하는 입자의 속도와 각속도로부터 곡률(curvature)을 정의(k=ω/υ)할 수 있으며, 식 (16)을 여기에 적용하면 식 (17)을 유도할 수 있다.
| (17) |
여기서 k는 곡률로 k=1/r의 관계를 가지고 있다. 식 (17)은 스키머 로봇이 속도 υx로 주행하면서 선회반경 r을 유지하고자 할 때 각속도 ω를 결정할 수 있다는 의미이며, 본 논문에서는 매 순간 식 (17)로부터 산출되는 ω를 각속도 참조값(reference) ωref로 설정하여 제어를 수행한다. 이때 υx에는 스키머 로봇의 현재 선속도 값으로 설정된다.
3.2 추종 제어 파라미터 조정 규칙
PP 알고리즘은 기본적으로 조향각의 제어방법만을 다루고 있으므로, 보다 정교한 움직임을 구현하고자 한다면 선속도의 제어방법에 대한 추가적인 고려가 필요하다. 인접한 두 경유점은 직선 경로를 형성하게 되는데, 스키머 로봇이 이 직선 경로를 이동하는 동안 가속, 등속, 감속의 속도 프로파일(velocity profile)을 가지도록 설계하고자 한다. 또한, 로봇의 위치가 경유점에 가까운 경우 견시거리 ld를 작게 하여 빠르게 목표 경로에 근접시키고, 이후 점차로 경유점으로부터 멀어지면서 견시거리를 크게 하여 안정적으로 경로에 안착시키고자 한다.
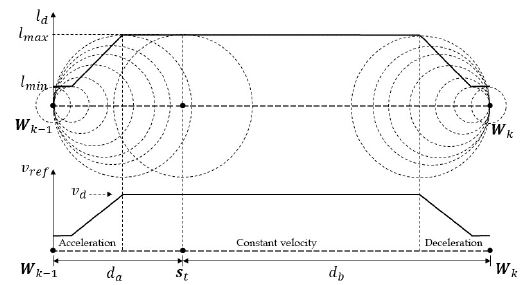
스키머 로봇이 Wk-1에서 Wk 방향으로 진행하는 상황을 고려하여 스키머 로봇의 현재 위치를 st라 할 때, 두 경유점 각각에 대한 거리를 da, db라 하자(Figure 4 참조). 또한 견시거리의 최대값 및 최소값을 각각 lmax, lmin이라 하자. 스키머 로봇의 현재 위치로부터 견시거리를 결정하는 규칙은 식 (18)과 같다.
| (18) |
여기서 La,Lb는 각각 출발점(Wk-1)과 목표점(Wk)에 대해 산출된 견시거리 후보로서 식 (19), 식 (20)과 같이 정의된다.
| (19) |
| (20) |
각각의 경우에 대한 견시거리로서 로봇의 현재 위치가 경유점 근방이면 그 거리에 비례하여 상대적으로 짧은 견시거리(≥lmin)가 설정되며, 경유점에서 충분히 먼 위치에 있을 때는 최대 견시거리(lmax)가 설정된다. 한편 스키머 로봇은 경로 추종 중 물리적으로 목표점(Wk)을 벗어날 수 있는데, 식 (20)의 ϵ은 이를 방지하기 위한 마진(margin)을 나타낸다.
PP 제어기법에서 견시거리가 너무 짧으면 경로 추종 시 불안정한 경향이 있다. 특히 높은 선속도로 회전하는 상황이라면 선회반경 또한 선속도에 비례하여 커지며, 이러한 경우 경로 추종 시 오버슈트가 발생한다. 이러한 경우 선속도를 적절하게 낮추게 되면 추종 안정 성능을 향상시킬 수 있다. 본 논문은 이러한 사항을 제어 알고리즘에 반영하고자 하며, Figure 4는 견시거리의 변화에 대응되는 속도 프로파일(velocity profile)의 생성 계획을 도시한 것이다. 즉 로봇이 경유점에서 점차로 멀어지거나 점차로 가까워지는 경우 견시거리에 비례하여 선속도 참조값 υref를 조정하고자 하며 이를 위한 조정 규칙은 식 (21)과 같다.
| (21) |
식 (21)을 통해 유추할 수 있듯이, 선속도 참조값은 원하는 속도(desired velocity) υd에 대해 [lmin/lmax,1]의 가중치 범위를 가지는 속도로 조정된다. 만일 lmin을 0으로 설정하면 υd에 대하여 0~100%의 속도 참조값이 산출될 수 있으므로 Figure 4의 속도 프로파일은 완전한 사다리꼴 형태가 된다. 식 (21)을 통해 선속도 참조값이 결정되면 스키머 로봇이 현재의 선회반경을 따라 추종될 수 있도록 각속도 참조값을 식 (22)와 같이 결정한다.
| (22) |
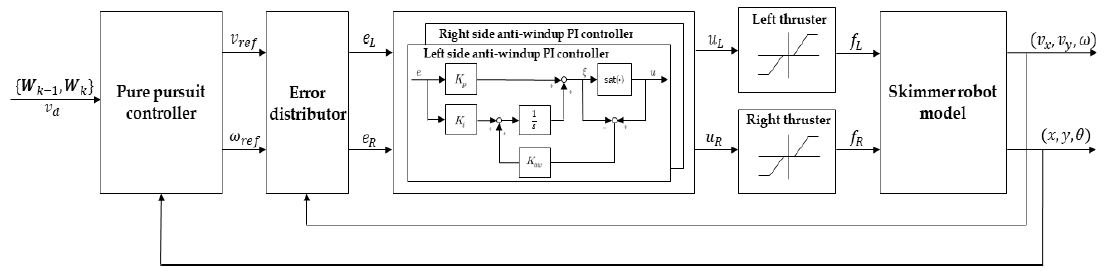
본 논문에서 제안된 스키머 로봇의 경로 추종 제어 알고리즘을 모두 도식화하면 Figure 5와 같다. PP 제어기는 두 개의 경유점 {Wk-1,Wk}과 속도 설정치 υd를 입력받아 로봇의 위치정보 (x,y,θ)의 피드백을 통해 선속도 및 각속도에 대한 참조값 (υref,ωref)을 산출한다. 오차분배기(error distributor)는 스키머 로봇의 선속도(υx) 및 각속도(ω)의 피드백 및 식 (10)의 변환과정을 통해 좌우 추진기의 제어입력용으로 이용될 오차를 산출한다. 이후 안티와인드업 PI제어기를 통해 스러스터를 구동시키며 최종적으로 로봇의 위치를 주어진 경로에 추종시키는 제어를 수행한다.
3.3 목표점 도달 판정 규칙
Figure 5의 경로 추종 제어 시스템을 통해 스키머 로봇이 현재의 경유 목표점 Wk 에 도달하게 되면 다음 단계의 경유점 쌍으로 갱신한 후 다시 경로추종 제어를 수행하게 된다. 이때 스키머 로봇이 경유 목표점에 도달했는지의 여부를 판정할 필요가 있다. 이를 위해 경유 목표점 Wk를 동차표현(homogeneous representation)하여 Wk=(xk,yk,1)⊤로 설정한다. 또한 본 논문에서는 로봇의 현재위치를 중심점으로 하는 원을 QR∈R3×3의 코닉행렬(conic matrix)로 표현한다. 앞 절에서 설명한 바와 같이 로봇의 위치가 목표점에 접근하게 되면 QR의 반경은 lmin이 될 것이므로 경유 목표점이 이 원 안에 위치하는 경우 목표점에 도달했다고 간주할 수 있다. 이를 수식으로 표현하면 식 (23)과 같다.
| (23) |
최소 견시거리 lmin은 3가지 관점에서 의미가 있는 파라미터이다. 사실상 lmin은 목표점 도달 판정을 위한 최소 거리, 경유시작/종료 시점에서의 경로 추종 속응성, 경유시작/종료시점에서의 속도결정과 밀접하게 관련되어 있는데, 이에 관해서는 다음 장의 모의실험 결과를 토대로 다시 살펴본다.
4. 실험결과 및 고찰
4.1 실험환경 설정
제안된 경로 추종 제어 시스템의 성능은 스키머 로봇의 수학적 모델을 기반으로 모의실험을 통해 평가된다. 모의실험은 파라미터의 자동 조정, 속도 제어기의 성능, 최소 견시거리(lmin)에 따른 주행특성 변화, PP 알고리즘의 추종 제어 성능의 관점에서 수행된다. 스키머 로봇의 동적 특성을 모사하기 위한 주요 시뮬레이션 파라미터는 Table 1과 같으며, 이들은 문헌[8]을 참고하여 설정되었다. 동적 모델 파라미터 값들은 문헌[8]의 선박과 본 논문에서 다루는 선박 간의 면적비(또는 체적비)에 의한 보정을 통해 산출되었다. 참고로 각 파라미터의 값은 소수점 셋째 자리에서 반올림되었다.
4.2 파라미터 자동 조정 및 속도 제어 실험
본 논문에서 제안된 경로 추종 제어시스템은 경유점 집합과 원하는 속도 설정값(υd)을 입력하면 견시거리, 선속도/가속도 참조값에 대한 프로파일을 자동적으로 생성한다. 이를 위한 모의실험 조건으로 스키머 로봇의 초기 상태를 (0,0,0)⊤로 설정하고 경유점의 좌표를 각각 (20, 0), (20, 5), (30, 5)로 설정하였다. 참고로 이러한 경우 W0=(0,0,1)⊤, W1=(20,0,1)⊤, W2=(20,5,1)⊤ 등과 같은 동차표현으로 경유점 쌍이 설정된다. PI 제어기의 경우 좌우 스러스터 제어에 대해 동일하게 Kp=1.5, Ki=3.0, Kaw=2.0으로 설정하였다. 각각의 게인 값은 로봇의 쓰레기 수거작업 시의 거동을 고려하여 속도 참조값 1m/s의 스텝 입력에 대하여 정착시간이 0.2초 이내가 되면서 오버슈트는 발생하지 않은 조건을 만족하도록 동조되었다. PP 경로 추종 제어기를 위한 파라미터로서 최대 견시거리 lmax=8.0m, 최소 견시거리 lmin=1.5m로 각각 설정하였으며 속도 설정치 υd=4.0m/s으로 설정하였다.
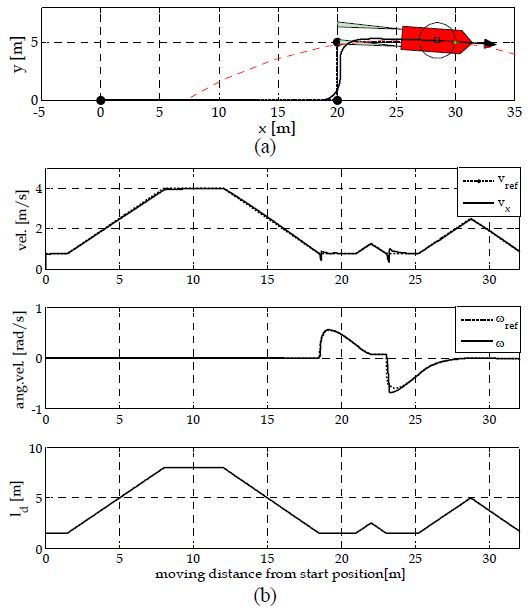
Figure 6은 상기 조건에서의 모의실험 결과를 나타낸다. Figure 6 (a)는 주어진 경유점에 대한 스키머 로봇의 추종궤적을 나타낸 것이며, 좌우방향에 대한 변침이 각각 한 번씩 이루어지는 곡선 궤적을 형성하고 있다. 이러한 주행 경로에 대해, Figure 6 (b)의 상단 2개 그래프는 각각 선속도 및 각속도에 대한 상태를 나타낸 것이다. 여기서 점선은 자동 파라미터 조정 규칙을 통해 생성된 속도 프로파일 및 각속도 프로파일을 나타낸다. 실선 부분은 안티와인드업 제어기를 통해 구현된 로봇의 선속도 및 각속도의 변화를 각각 나타내고 있다. 그림에서 나타난 바와 같이 스키머 로봇의 선속도 및 각속도는 각각의 참조값에 거의 겹쳐져 있음을 보이고 있는데, 이는 각 추진기의 제어를 위한 안티와인드업 PI제어기의 성능이 양호하게 동작하고 있음을 의미한다. Figure 6 (b)의 하단 그래프는 매 위치마다의 조정되고 있는 견시거리를 출력한 것이다. Figure 4에서 설계한 바와 같이 견시거리가 경유점 근방에서는 짧아지는 반면 양쪽 경유점으로부터 상대적으로 먼 거리에 있는 경우 최대 견시거리를 가지도록 조정되고 있음을 알 수 있다.
4.3 기존 PP 알고리즘과의 성능 비교
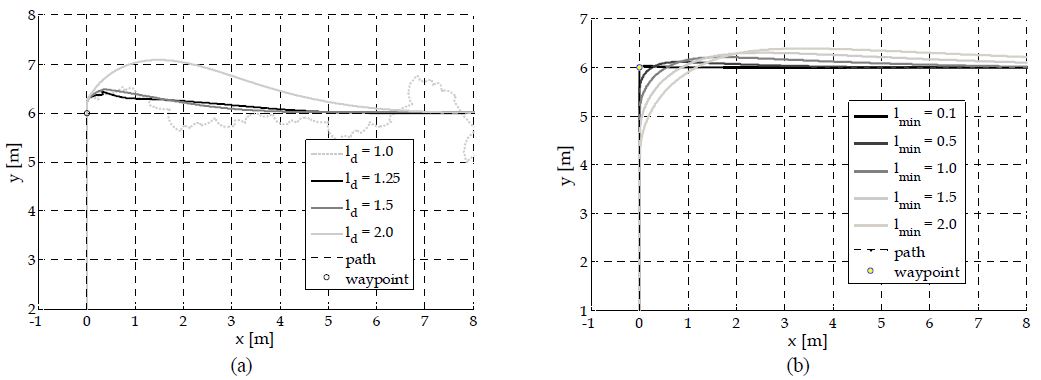
본 논문에서 제안된 경로추종제어 알고리즘은 기존의 퓨어퍼슈트 알고리즘을 개선한 것으로서 3.2절에 기술한 바와 같은 자동 파라미터 조정규칙이 적용되어 있다. 제안된 방법의 성능을 비교 평가하기 위하여, 기존의 퓨어퍼슈트 알고리즘과의 성능비교 실험을 수행하였다. 이때 실험 조건은 스키머 로봇의 초기상태를 (0,0,π/2)⊤로, 경유점을 W1:2={(0,6,1)⊤,(20,6,1)⊤}로 설정하였다. 또한 스키머 로봇의 속도는 υd=2.0m/s로 설정하였다. Figure 7 (a)는 고정된 견시거리(ld)를 가지는 기존의 PP 알고리즘이 적용된 실험결과를 나타낸 것이다. 참고로 가독성 향상을 위해 W1 근방 영역만을 확대하였다. Figure 7 (a)에 나타난 바와 같이 견시거리가 1.0인 경우 스키머 로봇의 궤적이 주어진 경로와 크게 벗어나며 자세 또한 안정화되지 못하고 있음을 알 수 있다. 반면 견시거리가 2.0인 경우 오버슈트가 비교적 크게 나타나고 있다. Figure 7 (a)를 토대로 보면 견시거리 파라미터의 적정수치는 1.5 ~ 2.0 사이인 것으로 평가되며, 이는 파라미터 수치에 따른 제어성능의 민감도가 다소 높음을 알 수 있다. Figure 7 (b)는 제안된 방법을 적용한 모의실험 결과를 나타낸 것으로 기존의 방법에 비하여 보다 안정된 결과를 보여주고 있음을 알 수 있다. 여기서 주목할 사항은 최소 견시거리(lmin)파라미터가 1.0 이하에서도 안정된 결과를 보여주며, 오히려 경로추종제어 오차가 현저히 줄어들고 있음을 알 수 있다. 이는 제안된 방법이 견시거리 및 선속도 설정값을 자동적으로 조정하도록 설계되어 있기 때문이다.
4.4 최소견시거리 파라미터(lmin)의 속성 분석
한편 3.2절에서 언급하였듯 최소 견시거리 파라미터인 lmin의 설정값은 스키머 로봇의 변곡점 주행특성에 영향을 미친다. Figure 7(b)는 앞 절에서와 동일한 실험조건에서 최소 견시거리를 {0.1, 0.5, 1.0, 1.5, 2.0}으로 각각 변경시켰을 때의 모의실험 결과를 나타낸다. 실험결과를 통해 알 수 있듯이 최소견시거리 파라미터는 변곡점에서의 선회반경과 수렴속도/오버슈트에 영향을 미침을 알 수 있다. 파라미터 값이 0.1 정도로 작은 경우에는 주어진 경로와 거의 일치하게 추종하지만 경유점에서 급작스런 선회가 이루어지고 있음을 추정할 수 있다. 물론 이 경우에도 “감속-회전-가속”의 모션 양상을 보이는데, 식 (21)의 계산식에 따라 회전시의 선속도 참조값은 설정속도 υd의 1.25%인 0.025m/s가 된다. 한편 파라미터의 값이 큰 경우(예: lmin=2.0)에는 경유점에 도착하기 2m지점부터 회전이 시작되고 있음을 알 수 있다. 이 경우의 선속도 참조값은 0.5m/s가 설정되며, 이 속도를 유지하면서 회전하게 되므로 회전반경이 다소 크지만 보다 높은 속도를 유지하면서도 유연한 회전운동을 구현할 수 있다. 다만, 이러한 경우 오버슈트가 비교적 커지고 수렴속도가 느려진다는 단점이 있다. 따라서 유연한 회전, 적절한 수렴속도/오버슈트 등을 고려하여 적절한 파라미터 값을 설정할 필요가 있다.
다음으로 최소 견시거리 설정값에 대한 경로 추종 오차를 분석하였다. 추종 오차는 스키머 로봇의 목표점이 W2로 바뀌는 시점부터 매 샘플시간(5ms)마다 기록되었으며 여기에서는 y축에 대한 오차만을 고려하였다. 이는 로봇의 경로가 두 경유점을 연결하는 직선으로 주어지기 때문이며, Figure 7에서 y=6의 직선에 대한 수직편차와 같다. 오차의 특성은 MAE(mean absolute error), 정상상태 오차 (SSE: steady state error), 최대값을 통해 분석되었고 그 결과는 Table 2에 열거하였다.
최소 견시거리 설정값이 0.1인 경우 MAE는 0.0109, SSE는 0.0007, 최대값는 0.0998로 조사되었다. 이들 수치들은 최소 견시거리 설정값이 증가할수록 높아지는 경향이 있었다. 최대값은 경유점이 바뀌는 순간의 오차로부터 기인한 것인데, 이는 최소 견시거리 설정값과 거의 같으며, 이는 또 현재의 목표 경유점에서 다음의 목표 경유점으로 바뀌는 시점과 관련된다. 따라서 최소 견시거리 설정값을 크게 하면 MAE, SSE, 최대값의 증가를 야기하는 반면 로봇은 더욱 부드러운 주행 특성을 보이게 된다.
4.5 수거 작업 시뮬레이션
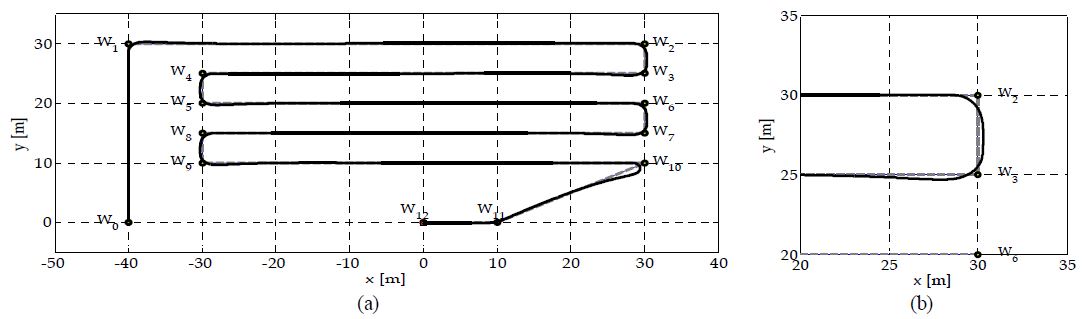
다음으로 스키머 로봇이 쓰레기 수거 작업 상황을 고려한 시뮬레이션을 수행하였다. 초기상태는 (-40,0,π/2)⊤으로 설정되었고 최소견시거리 파라미터 lmin는 1.5m로 설정되었다(시뮬레이션 결과의 가독성 확보 차원에서 설정). 로봇은 쓰레기 수거를 위해 (-40,30)의 위치로 이동한 후 지그재그 방식의 전범위 경로 순방을 통해 쓰레기 수거작업을 실시한다. 수거작업 종료지점인 (30,10)의 위치에 도달하면 모선으로 귀환한다. 이러한 작업 시나리오에 대한 시뮬레이션 수행 결과는 Figure 8 (a)와 같다. 각각의 경유점들은 그래프 상에 도시되어 있으며 로봇의 목표이동경로는 각각의 경유점들을 직선으로 연결한 경로(회색 점선으로 구분)가 된다. 로봇의 이동 궤적은 검정색 실선으로 표시되어 있는데 직각으로 꺾이는 회전 구간에서 비교적 큰 회전반경을 가지며 회전하고 있음을 알 수 있다. Figure 8 (b)는 W2와 W3 경유점 부근을 확대한 것으로서 두 경유점을 지날 때 보다 부드러운 회전이 되고 있음을 확인할 수 있다. 경유점 W10 근방은 기하학적으로 스키머 로봇의 급격한 회전을 요하는 지점으로 다른 경유점에 비해 오버슈트가 다소 크게 발생하고 있다. 시뮬레이션 상에서 W10에서의 변침각은 –153.43도가 되며 변침 시 식 (21)에 의해 계산된 2.0ㆍ(1.5/8.0) = 0.375m/s의 선속도를 유지하면서 회전하게 되므로 오버슈트가 필연적으로 발생하게 된다. 4.2절의 실험을 통해 확인하였듯이 최소 견시거리를 보다 작은 값(예: 0.5m)으로 선정하면 오버슈트를 줄일 수 있다. 한편 lmin이 0가 되는 경우 선속도 참조값이 0가 되므로 멈춘 상태에서 회전하는 모션이 구현됨을 참고할 필요가 있다. 따라서 lmin은 응용목적에 따라 오버슈트 정도와 회전 유연성을 고려하여 적절하게 선정될 수 있다.
5. 결 론
본 논문은 해상 쓰레기/부유물 수거를 위한 스키머 로봇의 경로 추종 제어 시스템의 구성방법을 다루었다. 이를 위한 접근 방법으로 내부에 안티와인드업 PI 속도제어 루프와 외부의 PP 기반 경로 추종 루프로 구성된 제어시스템을 제안하였다. 특히 경로 추종 제어에 있어 각속도 (또는 조향각)의 제어와 함께 선속도 제어를 위한 속도 프로파일의 자동적인 생성, 견시거리의 자동적인 조정을 동시에 수행할 수 있는 간단한 기법을 제안하였다. 시뮬레이션 결과 본 논문에서 제안된 기법은 당초 설계된 대로 동작함을 확인하였고, 스키머 로봇의 경로 추종에 있어서도 최소 견시거리 파라미터 설정에 따른 유연한 모션을 구현할 수 있었다.
그러나 로봇의 실용화를 위해서는 항공사진으로부터 정밀한 해상 지도 매핑, 에너지 및 외란을 고려한 최적 경로 계획, 장애물 감지 및 회피 등 다양한 추가 연구가 필요하며, 이는 추후 과제로 남긴다.
Author Contributions
Conceptualization, H. H. Kim and Y. S. Ha; Methodology, H. H. Kim; Validation, Y. S. Ha; Writing—Original Draft Preparation, H. H. Kim; Writing—Review & Editing, Y. S. Ha; Visualization, H. H. Kim; Supervision, Y. S. Ha; Funding Acquisition, Y. S. Ha;
References
- D.-H. Kim, A Study on National and International Laws on Marine Debris, M.S. Thesis, Department of Environmental Oceanography, Chonnam National University, Korea, 2017 (in Korean).
- Z. Lu, B. Shyrokau, B. Boulkroune, S. V. Aalst, and R. Happee, “Performance benchmark of state-of-the-art lateral path-following controllers,” IEEE 15th International Workshop on Advanced Motion Control (AMC), pp. 541-546, 2018.
- R. C. Coulter, Implementation of the Pure Pursuit Path Tracking Algorithm, Technical Report CMU-RI-TR-92-01, Robotics Institute, Carnegie Mellon University, USA, 1992.
-
T. I. Fossen, Handbook of Marine Craft Hydrodynamics and Motion Control, Wiley, 2011.
[https://doi.org/10.1002/9781119994138]

-
H. Ashrafiuon, K. R. Muske, L. C. McNinch, and R. A. Soltan, “Sliding-mode tracking control of surface vessels,” IEEE transactions on industrial electronics, vol. 55, no. 11, pp. 4004-4012, 2008.
[https://doi.org/10.1109/TIE.2008.2005933]

-
X. Miao, J. Lee, and B. Y. Kang, “Scalable coverage path planning for cleaning robot using rectangular map decomposition on large environments,” IEEE Access, vol. 6, pp. 38200-38215, 2018.
[https://doi.org/10.1109/ACCESS.2018.2853146]

- H. H. Kim, Vision-Based Object Recognition and 3-D Pose Estimation Using Conic Features, Ph.D. Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime University, Korea, 2012.
-
K. R. Muske, H. Ashrafiuon, G. Haas, R. McCloskey, and T. Flynn, “Identification of a control oriented nonlinear dynamic USV model,” 2008 American Control Conference, pp. 562-567, 2008.
[https://doi.org/10.1109/ACC.2008.4586551]