LNG 연료 기관용 재기화 시스템의 글리콜 온도제어를 위한 비선형 PID 제어

1. 서 론

최근 지구 온난화 현상이 가속화되면서 국제적으로 온실가스 배출에 대한 규제가 활발히 논의되어 왔다. IMO(International Maritime Organization)는 주요 오염원인 이산화탄소(CO₂), 질소산화물(NOx), 황산화물(SOx) 등의 기관 배출가스를 규제하고 있으며 발틱해, 북해, 북아메리카 해역은 이미 배출가스통제구역으로 발효되어 있다.

IMO 규제안에 따르면 CO₂와 관련해서 2013년 이후 건조되는 신조선에 대해서 EEDI(Energy Efficiency Design Index)를 적용하게 되는데, 총톤수 400톤 이상의 선박은 2025년까지 EEDI를 3차례에 걸쳐 30%까지 감축해야 하며, 이를 충족하지 못한 선박은 운항이 금지된다. 2021년부터 Tier III이 발효되어 신조 선박은 NOx를 Tier I에 비해 80% 정도 줄인 kwh당 1.96~3.4g으로 감축시켜야 하고, 2020년부터 선박 연료의 SOx 함유량 기준도 기존 3.5%에서 0.5%로 강화된다[1].

이와 같이 선박 배출가스의 규제를 강화함에 따라, 배출가스를 감소시키려는 방법 중의 하나는 친환경적 연료인 LNG(Liquefied Natural Gas)를 기관의 연료로 사용하는 것이다.

극저온의 LNG를 연료로 사용하기 위해서는 LNG 재기화 장치가 필요하며, LNG는 기화기(vaporizer)에서 글리콜 (glycol)로부터 에너지를 흡수하여 기화되고, 냉각된 글리콜은 다시 열교환기에서 고온의 스팀으로 가열된다.

셀-튜브형 열교환기의 온도제어와 관련된 연구로는 Choi가 기존의 선형 PID 제어기에 피드포워드 제어를 추가하여 주기관의 부하 변동에 따른 냉각수 온도 변화를 감소시켰고[2], Ahn 등은 안티와인드업(anti-windup)과 피드포워드제어 기법을 결합한 PID 제어기를 제안하였으며[3], 또한 주기관 자켓 냉각수의 온도제어를 위해 이중 루프 캐스케이드 온도제어 시스템을 제안하여 외란에 의한 냉각수의 급격한 온도변화를 완화시켰다[4].

그러나 많은 산업 프로세스들은 비선형이 강하고 운전 중에 파라미터가 변동될 수 있어서 이득이 고정된 제어기는 제한된 동작 구간에서는 효과적이지만 이를 벗어나면 성능이 저하되고 경우에 따라서는 불안정해질 수도 있다.

이와 같은 문제를 해결하기 위해 표준형 선형 PID 제어기의 구조에 비선형 요소를 추가하고 온라인으로 제어기 이득을 변경하는 일련의 연구들이 많이 수행되어 오고 있다. 비선형 PID 제어기의 이득을 온라인으로 변경하는 기법에는 오차신호를 비선형적으로 스케일링한 후, 이 스케일된 오차를 비례, 적분 및 미분 제어기에 각각 입력하여 비선형 이득을 구현하는 방법과 제어기의 세 이득을 비선형 함수로 직접 구현하는 방법 등이 있다.

전자에 의한 연구 예로 Seraji [5]는 비선형함수를 이용하여 오차신호를 비선형적으로 스케일링한 후 선형 PID 제어기에 입력하는 단순한 형태의 비선형 제어기를 제안하였다. 제어기 이득을 비선형 함수로 직접 구현하는 연구에는 비선형 함수로 가우스 오차함수(Gaussian error function), 하이퍼볼릭-시컨트 함수 및 지수함수를 많이 이용한다. Korkmaz [6]등은 가우스 오차함수를 이용하여 비선형 시변이득을 직접 구현하였으며 시변 이득에 포함되어 있는 파라미터를 유전알고리즘으로 동조하였다.

이러한 방법들은 제어 환경이 변해도 어느 정도 만족스런 결과를 주었지만 비선형 PID 제어에서의 잡음에 대한 문제 등 아직 개선해야 할 점이 많이 있다.

본 연구에서는 LNG 재기화 시스템의 2차측 글리콜의 출구 온도를 제어하기 위해 단순하면서도 구현이 쉬운 시그모이드 함수를 도입한 비선형 PID(Nonlinear PID; NPID) 제어기를 설계하고 RCGA(Real-Coded Genetic Algorithm)로 최적 동조하는 문제를 다룬다. 이상적인 미분동작의 한계성을 극복하기 위해 미분동작에 필터식을 가진 수정된 비선형 PID 제어기를 사용하며, 현장에서 흔히 접할 수 있는 포화기를 고려하여 제어기를 설계한다. 각 제어기 내에 있는 파라미터들은 RCGA를 기반으로 ITAE(Integral of time absolute error) 성능지수를 최소로 하는 관점에서 최적 동조된다[7].

제안한 방법은 LNG를 연료유로 사용하는 기관의 LNG 재기화 시스템에서 글리콜 온도 제어에 적용하고 다른 두 방법과 비교하여 그 유효성을 확인한다.

2. LNG 재기화시스템의 모델링

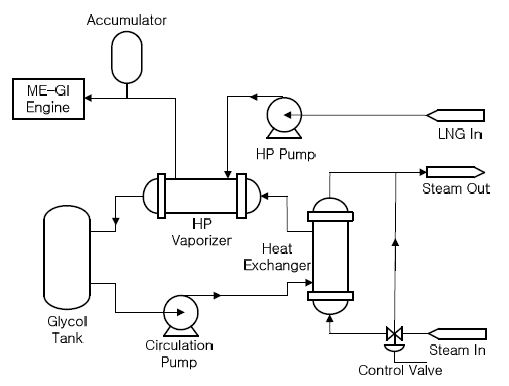
극저온의 LNG를 연료로 사용하기 위해서는 이것을 약 45~50°C의 가스로 만들어주기 위한 LNG 재기화 장치가 필요하다. Figure 1은 LNG를 연료유로 사용하는 선박용 기관을 위한 LNG 재기화 시스템의 한 예를 보여주며 1, 2차 측으로 구분된다[8].

Figure 1:

LNG regasification system for a main engine

1차측의 -163°C LNG는 HP펌프로 약 250-300bar까지 승압되어 고압 증발기를 거치면서 45~50°C의 가스 상태로 변환된 후 분사장치를 통해 엔진 실린더에 공급된다. 이때 LNG는 열매체인 글리콜(glycol)로부터 열을 공급받게 된다. 한편 2차측에서는 LNG와의 열교환으로 인해 온도가 낮아진 글리콜은 열교환기에서 다시 가열된다. 이때 스팀으로부터 열을 공급받게 되는데 그 열량은 제어기의 신호를 받아 공기압식 밸브에 의해 제어된다. 제어기에서 출력되는 전류신호는 전공(current to pressure; I/P) 변환기를 거치면서 공기압 신호로 변환되고, 이 공기압이 다이야프람 밸브에 입력되어 밸브 스템의 변위를 일으켜 스팀의 량을 조절한다.

Figure 2는 극저온 HP 펌프와 HP 증발기 실물의 한 예를 보여준다.

Figure 2:

Cryogenic HP pump and vaporizer (HHI)

제어기로부터 전기신호를 받아 공기압으로 변환해주는 I/P(current to pneumatic) 변환기는 식 (1)과 같이 증폭요소로 모델링 되고, 공기압을 받아 셀측 스팀 유량을 조절해주는 다이야프람 밸브의 모델은 식 (2)과 같이 근사 1차 시스템으로 나타낼 수 있다.

여기서 U_sat(s)와 P_r(s)는 각각 제어입력으로서 조작기 출력과 공기압이며 시간함수로 나타낼 때는 u_sat 및 p_r 등과 같이 소문자로 나타낸다(이후 s-함수를 t-함수로 표현할 때 모두 소문자로 표현함). q는 스팀유량을 의미하며, K_ip는 I/P 변환기의 이득상수, K_υ와 T_υ는 각각 다이야프람 밸브의 정상이득 및 시정수이다.

스팀과 글리콜 간에 열교환이 일어나는 셀-튜브형의 열교환기에서 스팀은 튜브 쪽으로 글리콜은 셀 쪽으로 흐른다. 열교환기 모델을 구할 때 글리콜의 입출력 유량은 같고, 공급 스팀의 온도는 일정하며, 열교환기와 파이프는 충분히 단열되어 외부 열손실이 없는 것으로 가정한다. 또한 글리콜의 출구온도 계측점의 위치가 열교환기로부터 다소 떨어져 있으면 시간지연을 고려해야 한다. 시간지연을 고려한 열교화기는 다음과 같은 전달함수로 표시할 수 있다.

여기서 θ_h는 글리콜 출구온도이며, L은 시간지연을 나타내고, K_h 및 T_h는 각각 열교환기의 정상이득 및 시정수를 의미한다.

일반적으로 셀-튜브형의 열교환기에서 고려될 수 있는 주요 외란은 글리콜의 유량과 온도 변화이다. 글리콜의 유량변화는 2차측의 순환펌프가 정속으로 운전되는 한 미미하지만, 선교의 지령에 따라 주기관의 회전속도를 갑작스럽게 변경하면 결국 LNG 분사량의 변화를 일으키고, 이로 인해 HP증발기를 거쳐 되돌아오는 글리콜의 온도변화는 크다고 할 수 있다. 따라서 글리콜의 온도 변화가 유량 변화에 비해 크다고 할 수 있으므로 외란은 다음 수식으로 근사화 할 수 있다.

여기서 d와 θ_d는 각각 글리콜의 입구 및 출구 온도변화, K_dis는 외란 모델의 정상이득을 의미한다.

한편 출력신호을 피드백하기 위한 센서로 열전대를 고려하면 열전대 센서 모델은 일반적으로 다음의 전달함수로 표현할 수 있다.

여기서 y는 출력으로서 글리콜 출구온도, y_s는 글리콜의 출구온도에 해당하는 센서 전류, K_s 및 T_s는 각각 센서의 정상이득 및 시정수를 의미한다.

식 (1) ~ 식 (5)를 결합한 개회로 시스템은 다음과 같이 표현된다.

여기서 u_sat는 제어입력으로서 조작기 출력, d는 외란으로서 글리콜 입구온도를 의미한다.

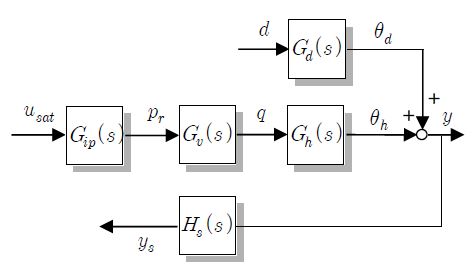
이를 블록선도로 표시하면 Figure 3과 같다.

Figure 3:

Block diagram of the plant

3. 제안하는 비선형 PID 제어기

3.1 비교대상의 PID 제어기

여기서는 비교 대상으로 사용할 Tyreus-Luyben 선형 PID 제어기(이후 TL-LPID 제어기라 함)와 Korkmaz의 비선형 PID 제어기(이후 K-NPID 제어기라 함)에 대해서 간단히 요약한다.

3.1.1 TL-LPID 제어기

TL-LPID 제어기는 표준 선형제어기의 구조를 가지며 기준값과 피드백 신호의 차인 오차신호 e(t)(이후 e로 표시함)를 이용하여 아래 식과 같이 제어입력 u(t)를 구한다.

$\[ u\left(t\right)=k_{p}e\left(t\right)+k_i{\int }_0^{t}e\left(\tau \right)d\tau +k_d\frac{de\left(t\right)}{dt} \]$

(7)

여기서 제어기의 비례, 적분 및 미분 이득은 임계이득 k_u와 임계주기 p_u를 이용하여 아래 식 (8)과 같이 구할 수 있다.

$\[ k_p=\frac{k_u}{2.2}, k_i=\frac{k_u}{4.84p_u}, k_d=\frac{k_u{p}_u}{13.86} \]$

(8)

3.1.2 K-NPID 제어기

Korkmaz의 방법[6]은 제어기의 비선형 이득을 직접 실현하는 방법으로서 비선형 비례이득은 식 (9)와 같이 오차의 크기에 따라 비선형적으로 조절된다.

$\[ K_p\left(e\right)=a_0+a_1\left|g\left(e\right)\right| \]$

(9)

여기서 a_i(i=0,1)는 양의 상수로서 사용자 조정 파라미터이고, g(e)는 다음과 같이 정의되는 오차함수(error function)이다.

$\[ g\left(e\right)=erf\left(e\right)=\frac{2}{\sqrt{\pi }}{\int }_0^e\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\tau }^2\right)d\tau \]$

(10)

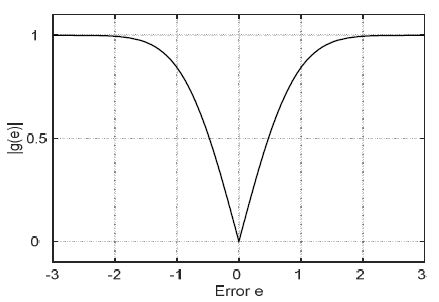
Figure 4는 오차의 변화에 대한 |g(e)|를 그린 것이며|g(e)|는 0을 중심으로 e가 0일 때 0, e가 음 또는 양으로 커질 때 1에 수렴하는 대칭함수이다. 따라서 K_p(e)는 a₀,a₁값에 따라 그 크기가 결정되며, 그 범위는 a₀≤K_p(e)≤a₀+a₁이다.

Figure 4:

Shape of |g(e )| to changes of e

비선형 적분이득은 식 (11)과 같다.

$\[ K_i\left(e\right)=b_0-b_1\left|g\left(e\right)\right| \]$

(11)

여기서 b_i(>0)(i=0,1)는 사용자에 의해 정해지는 파라미터이다. K_i(e)는 e→0이면 상한값 b₀에 수렴하고, 반대로 e→∞이면 하한값 b₀-b₁에 수렴한다.

비선형 미분이득은 식 (12)와 같다.

$\[ K_d\left(e\right)=c_0+c_1\left|g\left(e\right)\right| \]$

(12)

여기서 K_d(e)는 두 매개변수 c_i(>0)(i=0,1)을 가지는 비선형 함수이고, 하한값 c₀과 상한값 c₀+c₁ 사이의 값을 갖는다.

3.2 제안하는 NPID 제어기

본 연구에서는 표준형 PID 제어기에서 일어날 수 있는 미분폭주 현상을 줄이기 위해 미분동작에 필터항을 가진 수정된 PID 제어기를 사용한다. 수정된 PID 제어기의 전달함수 C(s)는 식 (14)와 같다.

$\[ u\left(t\right)=k_{p}g\left(e\right)+k_i{\int }_0^{t}g\left(e\right)d\tau +k_d\frac{dg\left(e\right)}{dt} \]$

(13)

$\[ C\left(s\right)=k_p+\frac{k_i}{s}+\frac{k_{d}s}{1+T_{f}s} \]$

(14)

여기서 k_p, k_i 및 k_d는 각각 선형제어기의 비례이득, 적분이득 및 미분이득이다. T_f=k_d/(Nk_p)이고 N은 8~20 사이에 경험적으로 정해지는 상수이며, 여기서는 10이 사용된다[9].

오차를 비선형적으로 스케일링하기 위해 식 (15)와 같은 시그모이드(sigmoid) 함수를 이용하며 이 스케일된 오차를 선형 PID 제어기에 입력하여 제어입력을 비선형적으로 구현한다.

$\[ g\left(e\right)=a_0+a_1\left[\frac{2}{1+\mathrm{e}\mathrm{x}\mathrm{p}\left(-a_{2}e\right)}-1\right] \]$

(15)

여기서 a_i(i=0,1,2)는 사용자에 의해 정해지는 양의 상수이다. g(e)는 e→ −∞이면 하한값 a_min=a₀-a₁에 수렴하고 반대로 e→∞이면 상한값 a_max=a₀+a₁에 수렴하며 e→0이면 g(e)=a₀이다. g(e)≥0인 것을 확보하기 위해 a₀≥a₁의 관계를 가진다. a₁은 g(e)의 범위를, a₂는 g(e)의 변화율을 결정한다.

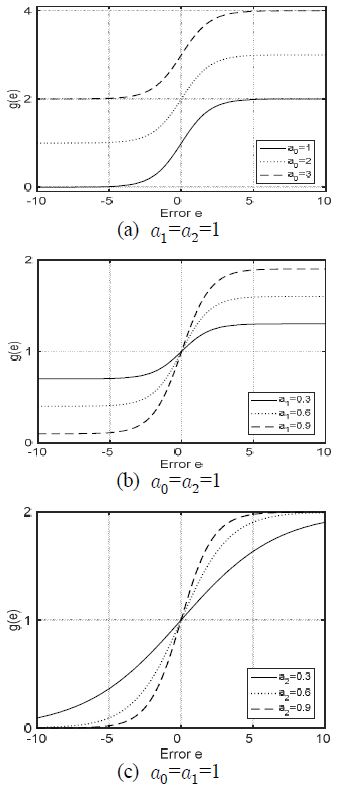
Figure 5 (a)는 a₁=a₂=1로 고정하고 a₀=1, 2, 3으로 변경했을 때, Figure 5 (b)는 a₀=a₂=1로 고정하고 a₁=0.3, 0.6, 0.9로 변경했을 때, Figure 5 (c)는 a₀=a₁=1로 고정하고 a₂=0.3, 0.6, 0.9로 변경했을 때의 g(e)의 모양을 보여준다.

Figure 5:

shapes of g(e ) to change of ai

3.3 NPID 제어기의 동조

앞서 제안한 NPID 제어기는 총 6개의 조정해야 할 파라미터가 존재한다. 각 파라미터를 동조할 때 실제 조작기의 동작에는 한계가 있으므로 제어기와 플랜트 사이에 다음과 같은 비선형 포화기가 있는 것으로 가정하며 포화기의 최소값 u_min은 4[mA], u_max는 20[mA]로 하였다.

(16)

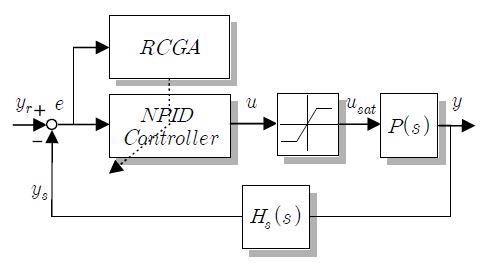
이들 파라미터에 대한 동조는 IP 변환기, 제어용 밸브, 포화기, 열교환기 및 센서로 이루어진 전체 제어시스템에서 원하는 설정치 추종 성능을 얻을 수 있도록 적절히 수행된다. 이때 일어나는 다변수 최적화 문제는 Figure 6과 같은 시스템에서 RCGA를 이용하여 해결한다[7]. Figure 6에서 플랜트 P(s)는 식 (6)에서 외란 입력에 대한 부분을 제외한 것이다.

Figure 6:

Tuning of the NPID controller with a saturator

RCGA로 제어기의 파라미터를 동조할 때 성능이 좋고 나쁨을 계량하기 위해 식 (17)의 IAE 성능지수를 사용한다.

$\[ J\left(\varphi \right)={\int }_0^{t_f}\left|y_r\left(t\right)-y_s\left(t\right)\right|dt \]$

(17)

여기서 [k_p,k_i,k_d,a₀,a₁,a₂]∈R⁶은 제안한 NPID 제어기의 파라미터로 구성되는 벡터이고 y_r(t)은 설정값, y_s(t)는 센서의 출력이며, 적분시각 t_f는 이후의 적분값이 무시될 수 있도록 충분히 큰 값이다.

RCGA로 조정 파라미터를 최적화 할 때 집단의 크기 Psize= 50, 교배확률 Pc= 0.9, 돌연변이 확률 Pm= 0.05, 돌연변이 매개변수 b= 5를 사용하였으며, 각 파라미터는 구간 0≤k_p≤50, 0≤k_i≤10, 0≤k_d≤300, 0≤a₀,a₁,a₂≤1에서탐색되었다. 그리고 K-NPID 제어기의 파라미터는 0≤a₀,a₁≤50, 0≤b₀,b₁≤10, 0≤c₀,c₁≤200 에서 탐색되었다.

모의실험에서 사용된 IP 변환기, 제어용 밸브, 포화기, 열교환기의 데이터는 Table 1과 같으며, 동조된 결과는 Table 2에 정리하여 나타내었다.

Table 1:

Parameters of the plant

Table 2:

Tuned controller parameters

4. 시뮬레이션 및 검토

4.1 설정치 변경에 대한 응답

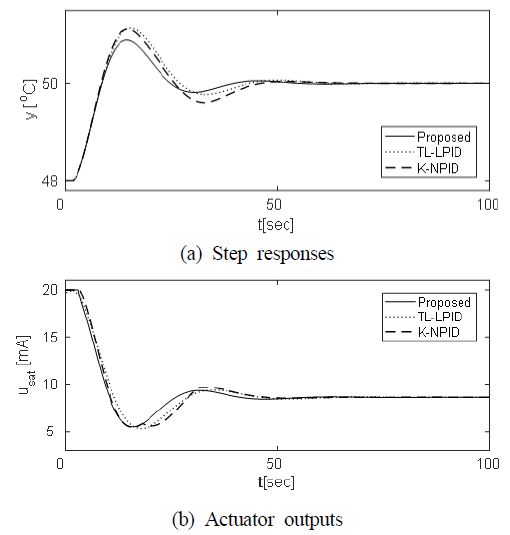
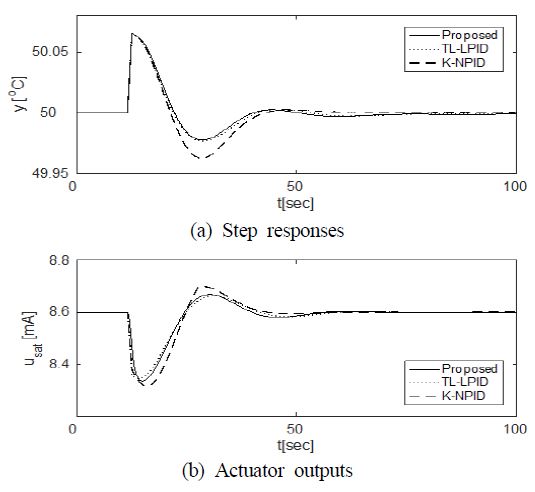
LNG를 연료유로 사용하는 기관의 경우 워밍-업(warm-ing-up) 기간에 –163°C의 LNG를 35~55°C의 온도로 점차적으로 가열하여야 한다. 이를 위해 기관사들은 시간차를 두면서 여러 단계(step by step)로 2차측의 글리콜 출구온도를 증가시킨다. Figure 7은 제안한 제어기의 설정값 추종성능을 확인하기 위해 2차측 열교환기의 글리콜 출구온도를 48°C에서 50°C로 변경했을 때 응답과 제어입력인 조작기 출력 및 각 이득의 변화를 나타낸 것이다.

Figure 7:

Step responses and actuator outputs when the set-point is step-wisely changed from 48[℃] to 50[℃]

또한, 각 제어기들의 성능을 정량적으로 평가하기 위해 상승시간 t_r(=t₉₀-t₁₀), 피크시간 t_p, 최대오버슈트 M_p, 2% 정정시간 t_s, 절대오차의 적분(Integral of Absolute Error: IAE)을 Table 3에 요약하여 나타내었다.

Table 3:

Set-point tracking performances

Figure 7과 Table 3에서 알 수 있듯이 세 방법 모두 정상편차 없이 설정값에 수렴하면서 비슷한 응답특성을 나타내지만 제안한 방법이 다른 두 방법보다 최대오버슈트, 정정시간, IAE가 더욱 작음을 확인할 수 있다.

4.2 잡음 억제에 대한 응답

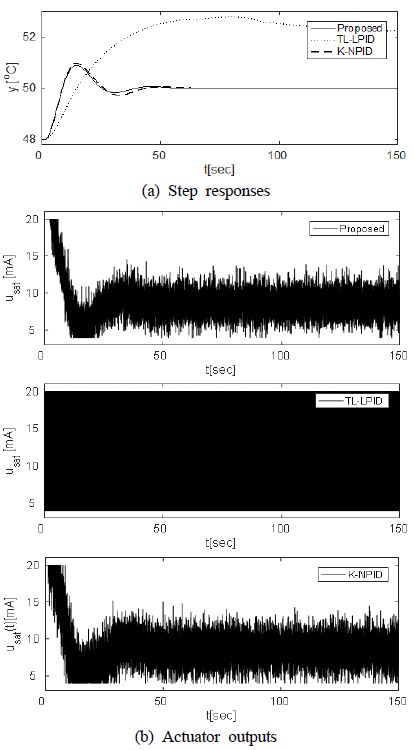
실제 적용에서는 계측잡음의 포함될 수 있다. 잡음에 대해 제안한 NPID 제어기의 강인성을 확인하기 위해 글리콜 출구온도를 계측할 때 N(0,0.005²)인 가우시안 백색잡음에 의해 교란되는 것으로 간주하고 시뮬레이션을 실시하였다.

Figure 8을 보면 제안한 제어기와 K-NPID 제어기는 계측잡음이 있더라도 성능 변화가 거의 없지만 TL-LPID 제어기는 미분폭주 현상으로 잡음에 직접적으로 영향을 받아 응답이 심하게 왜곡되어 설정치를 거의 추종하지 못하고 제어입력이 포화기의 상한값과 하한값을 반복하면서 심하게 교란되는 것을 볼 수 있다.

Figure 8:

Step responses and actuator outputs under Gaussian noise N(0,0.0052)

4.3 파라미터 변화에 대한 응답

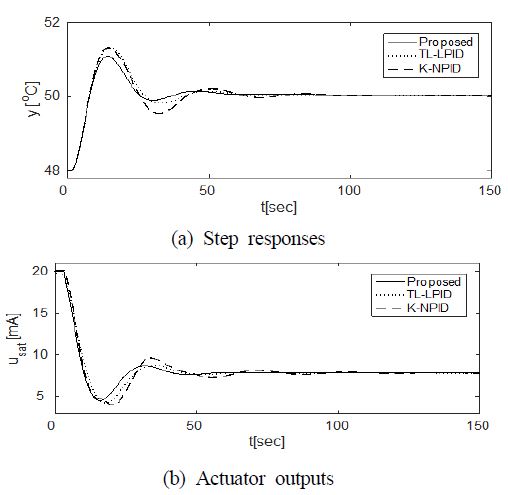
파라미터 변동에 대한 제어기의 강인성을 확인하기 위해 열교환기의 정상이득과 시정수를 동시에 10% 증가시킨 상태에서 글리콜 출구온도 48℃로 운전 중 50℃로 계단입력을 가하여 보았다. Figure 9와 정량적 성능 비교를 요약한 Table 4를 보면 세 방법 모두 비슷한 성능을 보이고 있지만 제안한 방법이 다른 두 방법보다 최대오버슈트, 상승시간, 정정시간, IAE 등의 모든 면에서 우수함을 알 수 있다.

Figure 9:

Step responses to parameter changes (Kh=2.99→ 3.3, Th= 30→33)

Table 4:

Set-point tracking performances Parameter changes

4.4 외란에 대한 응답

외란에 대해서도 제안한 제어기의 강인함을 확인하기 위해 글리콜 출구온도 50℃ 로 운전되고 있는 상태에서 10초 시점에 시작하여 1초에 2℃씩 변하는 램프(ramp)형 외란을 1초 동안 가하여 보았다.

Figure 10은 정상상태로 운전 중 램프형의 외란이 가해진 경우의 응답과 입력을 나타낸 것이다. 이 경우에도 세 방법 모두 비슷한 성능을 보이고 있지만 제안한 방법이 다른 두 방법보다 우수함을 알 수 있다.

Figure 10:

Step responses and saturator outputs under disturbance

5. 결 론

본 연구에서는 LNG를 연료로 사용하는 선박용 기관의 LNG 재기화 시스템에서 글리콜의 출구 온도를 제어하기 위한 비선형 PID 제어기를 제안하였다. 제어기의 비선형 이득은 시그모이드와 적절한 파라미터에 의해 구현되며 이들 파라미터들은 유전알고리즘을 기반으로 ITAE 성능지수를 최소로 하는 관점에서 최적 동조되었다. 이상적인 미분동작의 한계성을 극복하기 위해 미분동작에 필터를 추가하였으며 포화기도 고려하여 제어기를 설계하였다.

제안한 방법은 LNG를 연료유로 사용하는 기관의 LNG 재기화 시스템에서 글리콜의 온도 제어에 적용하였고 그 성능을 검정하기 위해 다른 두 방법과 비교한 결과 제어성능이 우수함을 확인할 수 있었다.

Author Contributions

The research presented in this paper was wholly contributed by the author.

References

• IMO, Green house gas emissions from ships, Phase 1 Report, 2008.
• S. Choi, “Configuration and analysis of a feed-forward control system for jacket cooling water temperature of marine prime diesel engine,” Journal of the Korean Society of Marine Engineering, vol. 32, no. 8, pp. 1303-1308, 2008. [https://doi.org/10.5916/jkosme.2008.32.8.1303]
• J. K. Ahn, G. B. So, J. Y. Lee, Y. H. Lee, M. O. So, and G. G. Jin, “PID control of a shell and tube heat exchanger system incorporating feedforward control and anti-windup techniques,” Journal of Institute of Control, Robotics and Systems, vol. 20, no. 5, pp. 543-550, 2014. [https://doi.org/10.5302/J.ICROS.2014.14.0009]
• J. K. Ahn, M. O. So, “Cascade temperature control for jacket cooling-water system of two-stroke low speed marine main diesel engine,” Journal of the Korean Society of Marine Engineering, vol. 42, no. 6, pp. 457-462, 2018. [https://doi.org/10.5916/jkosme.2018.42.6.457]
• H. Seraji, “A new class of nonlinear PID controllers,” 5th IFAC Symposium on Robot Control 1997 (SYROCO '97), pp. 65-71, Nantes, France, 1997. [https://doi.org/10.1016/S1474-6670(17)44245-5]
• M. Korkmaz, O. Aydogdu, and H. Dogan, “Design and performance comparison of variable parameter nonlinear PID controller and genetic algorithm based PID controller,” Proceedings of 2012 IEEE International Symposium on Innovations in Intelligent Systems and Applications, pp. 1-5, Turkey, 2012. [https://doi.org/10.1109/INISTA.2012.6246935]
• G. Jin and S. Joo, “A study on a real-coded genetic algorithm,” Journal of Control, Automation and Systems Engineering, vol. 6, no. 4, pp. 268-275, 2000.
• G. B. So, H. S. Yi, Y. D. Son, and G. G. Jin, “Temperature control of a regasification system for LNG-fuelled marine engines using nonlinear control technique,” International Journal of Control, Automation and Systems, vol. 16, no. 6, pp. 3047-3054, 2018. [https://doi.org/10.1007/s12555-018-0179-6]
• K. J. Åström and T. Hägglund, Advanced PID control, Durham, USA: ISA-The instrumentation, Systems, and Automation Society, 2006.