선박 자동 계류를 위한 슬라이딩 모드 제어시스템 설계
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
자동 계류 장치는 기존의 로프 기반의 계류 방식이 아닌 선체부착장치와 매니퓰레이터 메커니즘으로 구성된 새로운 개념의 선박 계류 장치이다. 본 논문은 자동 계류 장치를 이용한 선박의 계류 상황을 고려하여, 외란에 의해 동요하는 선박을 안정적으로 계류시키기 위한 제어 기법을 다룬다. 문제의 단순화와 더불어 자동계류를 위한 제어기 설계에 초점을 맞추기 위해 선박의 운동방정식은 스웨이-히브-롤 축에 대한 3자유도 운동방정식을 고려한다. 매니퓰레이터 메커니즘은 2자유도 회전관절을 가진 것으로 가정한 후 외란에 의해 동요하는 선박의 위치를 안정화시킬 수 있는 슬라이딩 모드 제어기를 설계한다. 본 논문에서 제안된 자동 계류 제어기법은 몇 가지 외란 조건에 대한 시뮬레이션을 통해 효용성이 평가된다.
Abstract
An automatic mooring device is a novel system based on hull holding and manipulating mechanisms (instead of the rope-based traditional method) that help in mooring a vessel. With regard to automatic mooring devices, this paper deals with a control system for keeping stable performance in which the vessel undergoes unintended motions due to external forces. For problem simplexity and to focus on the design of a control system, a 3-DOF sway-heave-roll dynamic model for a vessel is considered in this paper. Furthermore, we assume that the automatic mooring device has a 2-DOF manipulator and design a sliding mode control system that can stabilize a vessel against external disturbances. Simulations under various wind force conditions, as external disturbances, were performed to verify the effectiveness of the proposed method.
Keywords:
Automatic mooring device, Sliding mode control, Manipulator, Sway-heave-roll motion키워드:
자동계류장치, 슬라이딩모드제어, 매니퓰레이터, 스웨이-히브-롤 모션1. 서 론
최근 전 세계적으로 인공지능 및 정보통신 기술이 집약된 자율운항선박의 개발이 진행되고 있다. 자율운항선박에 있어 핵심적인 기술은 다양한 외적 요인들을 고려한 최적항로의 계획, 장애물 인지 및 회피를 통한 목적지로의 자율적인 운항 등을 포함한다. 이러한 핵심기술들은 오랫동안 축적되어 온 로봇공학 분야의 자율항법기술(autonomous navigation techniques)들과 최근 주목받고 있는 기계학습(machine learning), 인공지능(artificial intelligence: AI) 기술들을 토대로 활발히 연구되고 있다.
한편, 자율운항선박이 목적지에 도착하여 항만부두에 접안하는 상황에서 선박의 계류 방식에 관해 고려할 필요가 있다. 로프(rope) 기반의 전통적인 방식으로 자율운항선박의 계류작업을 수행하는 경우, 많은 인력과 시간이 소요됨은 물론 안전상의 문제 또한 간과할 수 없다. 특히 자율운항선박이 인간의 개입을 최소로 하는 개념으로 구현된 AI 기반의 자동화 시스템임을 감안한다면, 선박의 계류작업에 있어서도 자동화가 가능한 구조의 계류 메커니즘을 마련할 필요가 있다.
최근 유럽을 중심으로 전통적인 로프 기반의 계류방식을 탈피하여 새로운 방식의 계류 장치들이 개발되고 있다. 스위스의 카보텍(Cavotec), 스웨덴의 Trelleborg, 네델란드의 Mampaey은 자동계류장치를 개발하고 있는 기업이며, 특히 카보텍[1]은 자동계류장치에 있어 20년 이상의 오랜 기술력을 가지고 있다. 카보텍은 1998년 뉴질랜드의 픽톤(Picton)항에서 여객선 Aratere호를 통해 선박장착형 자동계류시스템(ship based automatic mooring system)을 출시하였다[2]. 또한 2003년에는 호주 멜버른(Melbourne)항에 부두장착형 자동계류시스템(shore based automatic mooring system) MoorMaster-400 모델 4기를 이용한 선박계류시스템이 출시되어 현재까지 운용되고 있다[3]. 이를 시작으로 2017년 기준 전 세계 46개의 항만에 자동계류시스템이 설치되어 운용되고 있다. 일부 항만에서는 실제 운용하고 있는 자동계류시스템에 관한 분석 사례를 보고한 바 있다[4][5]. 국내의 경우, 선대선(ship-to-ship) 도킹(docking)을 목적으로 자동도킹시스템이 개발된 사례가 있다[6].
전통적인 로프기반의 계류방식에 비해 부두장착형 자동계류장치가 가지는 가장 큰 차별점은 선박에 넓은 패드(pad)를 접촉시켜 직접 선체를 부착시킨다는 점과 이 패드의 위치를 부두에 설치된 매니퓰레이터 메커니즘을 이용하여 조절한다는 점이다. 이 구조는 로봇팔과 매우 유사한 구조로서 액추에이터를 통해 로봇 말단부를 제어하는 구조이며 기존 로프기반 방식에 비해 제어 및 자동화가 용이하다. 선체 부착용 패드는 자기(magnetism)식, 진공(vacuum)식 등을 고려할 수 있으나 진공식 흡착패드가 주로 이용된다. 진공식 흡착패드 역시 진공펌프의 전기적 제어를 통해 선체에 탈·부착되는 기능을 제어할 수 있으므로 로프를 선체에 고정하는 것에 비해 자동화가 유리하다. 이러한 관점에서 자동계류시스템을 이용하는 경우 자율운항선박의 접·이안 및 계류작업에 있어 기술적으로 선박의 AI시스템과 상대적으로 쉽게 연동될 수 있는 대안이 될 수 있다.
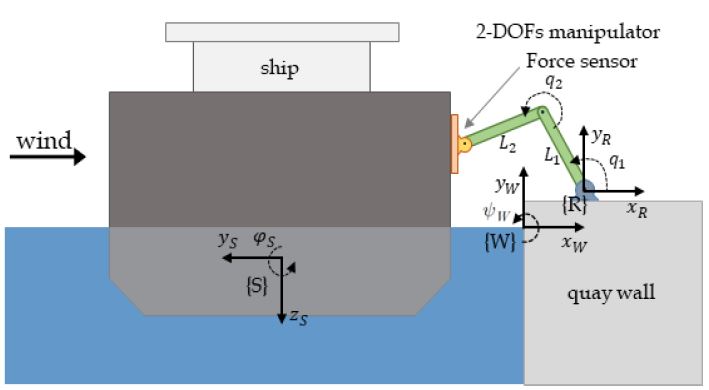
본 연구는 자율운항선박이 자동계류장치를 통해 접·이안 및 계류 중인 미래의 상황을 가정하여, 자동계류장치의 필요한 기능들을 정의하고 이를 위한 방법론을 정립하고자 한다. 이러한 목표 하에 본 논문에서는 우선 외란으로 기인하는 선박의 동요를 안정화시키기 위한 자동계류 제어기법에 초점을 맞춘다. 접·이안 및 계류 중인 선박은 바람, 파도, 흘수변화 등의 외적 요인으로 인한 동요가 발생되며, 자동계류장치가 선체에 접촉하는 순간부터는 선박의 이러한 동요를 완충시키면서 적절한 위치/힘 제어를 통해 선박을 안정화시킬 필요가 있다. 본 논문에서는 이러한 상황을 모사하기 위한 시뮬레이션 환경과 외란에 의해 동요하는 선박을 안정화시키기 위한 제어 시스템을 설계하고자 한다. Figure 1은 본 논문에서 구현하고자 하는 시뮬레이션 환경 및 목적을 나타내는 개념도이다. 우선 선박은 스웨이-히브-롤(sway-heave-roll) 모션을 고려한 3자유도 모델로 근사된다. 또한 자동계류장치가 2자유도의 매니퓰레이터 구조를 가진다는 가정 하에 두 시스템간의 동적 상호작용 모델을 구축한다. 또한 외란에 의해 발생되는 선박의 운동을 안정화시키면서 말단부의 위치를 제어하기 위한 슬라이딩 모드 제어 시스템을 설계한다.
본 논문의 구성은 다음과 같다. 제 2장에서는 선박의 동적 모델 및 외란 모델을 기술한다. 제 3장에서는 2자유도 매니퓰레이터 로봇의 동적 모델 및 선박 모델과의 동적 상호작용 모델을 설명한다. 제 4장에서는 슬라이딩 모드 제어시스템의 설계 방법을 논한다. 제 5장에서는 다양한 외란 조건에 대한 시뮬레이션 결과를 기술하고, 마지막으로 제 6장에서 결론을 맺는다.
2. 외력을 고려한 선박의 동적 모델
2.1 좌표계의 구분
본 논문에서는 Figure 1과 같이 선박과 로봇이 상호작용을 수행하는 자동 계류 메커니즘을 다룬다. 기술과정에서의 모호함을 줄이기 위해, 본 논문에서는 각 시스템의 좌표계를 다음과 같이 구분하여 표기한다. 우선 선박의 선체고정좌표계를 {S}라 하고 각 축은 xS,yS,zS라 표기한다. 로봇좌표계는 {R}로 표기하고 각 축은 xR,yR,zR이라 표기한다. 또한 월드좌표계를 {W}로 나타내고 각 축을 xW,yW,zW라 표기한다.
2.2 3차원 선박 모델
본 논문에서는 자동계류장치를 통해 계류 중인 선박을 대상으로, 외력에 의해 동요하는 선박의 운동을 안정화시킬 수 있는 제어기의 설계방법을 다루고 있다. 이를 위해 선박의 운동을 구현하기 위한 모델이 필요한데, 본 논문에서는 우선 SNAME 표기법에 따라 선박에 작용하는 외력과 모멘트를 각각 f0=(X,Y,Z)⊤, m0=(K,M,N)⊤라 한다. 그러면 선박의 6자유도 운동방정식은 뉴튼-오일러(Newton-Euler) 방법을 이용하여 식 (1)과 식 (2)의 관계로 나타낼 수 있다[4].
| (1) |
| (2) |
여기서 υ0=(u,υ,w)⊤, ω=(p,q,r)⊤, rG=(xG,yG,zG)⊤는 각각 선박의 선속도, 각속도, 무게중심좌표를 나타낸다. 문제의 간략화를 위해 선박 운동방정식을 yz-평면에 적용한 스웨이-히브-롤(sway-heave-roll) 모델을 고려한다. 이는 식 (1)과 식 (2)의 6자유도 선박 운동방정식에 선체고정좌표계에서 묘사되는 u, q, r을 0으로 설정한 선속도 및 각속도 벡터 υ0=(0,υ,w)⊤, ω=(p,0,0)⊤를 적용하여 유도할 수 있다. 선박의 대칭성을 고려하여 무게중심좌표를 rG=(0,0,zG)⊤로, 선박의 좌표계를 관성행렬 I0가 대칭행렬이 되도록 설정한다. 이를 적용하면 선박의 스웨이-히브-롤 모델은 식 (3) ~ 식 (5)와 같이 유도된다.
| (3) |
| (4) |
| (5) |
여기서 m은 선박의 질량을 나타내고 Ix는 x-축에 대한 선박의 관성모멘트를 나타낸다.
월드좌표계에서 표현되는 선박의 xW,yW축 위치 및 롤링 각도에 대해 상태변수벡터 η를 도입하여 η=(xs,ys,ψs)⊤로 정의한다. 또한 선체고정좌표계 {S}에서 묘사되는 롤 축 각속도와 yS,zS축 방향의 선속도에 대해 상태변수벡터 ν를 도입하여 ν=(p,υ,w)⊤라 한다. 본 논문에서는 뉴튼-오일러 동역학으로부터 유도된 식 (3) ~ 식 (5)의 운동방정식에 더하여 선체운동에 영향을 미치는 추가적인 힘을 고려한다. 우선 선체에 작용하는 유체감쇠력(hydrodynamic damping, ds(ν)로 표기)을 고려한다. 유체감쇠력은 선체가 유체와 접할 때 발생하는 다양한 저항력들의 합으로 구성되며 수조실험 등을 통해 추정되는 것이 일반적이지만, 본 논문에서는 선박의 속도 항에 대한 선형함수라 간주하여 점성마찰항력(viscous friction)만을 적용한다. 다음으로 복원력 항은 gs(η)으로 표기하며, 중력 및 부력에 관한 관계를 기술한다[7]. 여기서 복원력 항은 월드좌표계 {W}에서 정의되는 상태변수 벡터 η에 대한 벡터함수이다.
선체고정좌표계 {S}상에서 선체에 작용하는 외력을 통칭하여 τext로 표기하며 바람, 파도, 조류 등에 의한 외력 뿐 아니라, 자동계류장치가 선박과 상호작용하면서 발생되는 힘을 포함한다. τs는 선박의 추력을 나타내는 제어 입력 항으로 사용되는 경우가 일반적이지만, 본 논문에서는 선박이 정지된 경우를 가정하며 별도의 추력을 발생시키지는 않는다.
앞에서 기술한 내용을 종합하여 선박의 운동방정식을 유도하면 식 (6)과 같다.
| (6) |
여기서
| (7) |
| (8) |
| (9) |
| (10) |
선체고정좌표계의 상태변수벡터 ν는 식 (11)의 변환관계를 통해 월드좌표계에서의 속도 및 각속도로 나타낼 수 있다.
| (11) |
여기서
| (12) |
본 논문에서는 선박이 항만부두에 접안하여 자동계류장치를 통해 계류된 상태를 다루고 있으므로 부가질량 및 관성(added mass and inertia)는 없는 것으로 간주한다. 유체항력 d(ν)의 Xp, Xυ, Xw는 각 축에 대한 유체항력계수를 나타낸다. 복원력 항인 gs(η)에서 ρ는 유체밀도(water den-sity)를 나타내고, Aw는 유체에 담긴 선박의 수평단면적(water plane area)을, dw는 선박의 흘수(draft)를, 는 횡방향의 경심 높이(transverse metacentric height)를 각각 나타낸다. 식 (10)에서 나타나 있듯이 부력 산출에 필요한 선박의 배수용적은 선박의 흘수에 따라 구해지는 근사치(Awdw)를 적용하여 산출된다. 참고로 식 (10)은 월드좌표계상의 중력과 부력과의 관계를 식 (12)의 역변환()을 통해 유도된 식이다. 한편 선박의 는 선체의 형상과 롤링, 피칭 각도에 따른 부력중심의 변화 등을 고려하여 실시간으로 연산되어야 하나, 본 논문에서는 선박의 수직절단면이 직사각형이라는 가정 하에 의 근사치를 산출[8]하여 이를 시뮬레이션에 활용한다.
2.3 바람 모델
일반적으로 선박에 작용하는 외력으로 바람, 파도, 조류 등이 고려되지만, 항만 부두 내에 계류 중인 선박의 여건을 고려하여 풍력을 주요 외력으로 간주한다. 본 논문에서 이용되는 바람모델은 풍속(wind speed) VR과 방향각 γR 요소로 구성된 모델을 이용한다. 참고로 본 논문은 yz축 상의 선박운동만을 고려할 것이므로 풍력 방향각 γR은 상수(90도)로 간주한다. 본 논문에서 이용되는 바람모델에서 시정수 및 이득은 해리스 스펙트럼(Harris spectrum)의 1차 근사식을 따른다고 가정한다. 1차 해리스 스펙트럼은
| (13) |
로 표현되며, 이득 및 시정수는 각각 과 같다[4]. 이때 k는 난류인자(turbulence factor)로서 0.05의 값을 가지고, Vw(10)은 해상 10m 높이에서의 평균 풍속(unit: knots)을 나타낸다. 본 논문은 입력을 평균풍속으로 하고 시정수 TL로 표현되는 1차 시스템에 더하여 문헌[7]에서 제시된 해리스 스펙트럼 모델을 조합하여 바람모델을 구성한다. 상태변수 x1을 풍속으로, x2를 해리스 스펙트럼으로 표현되는 부가 풍속이라 정의하자. 본 논문에서 이용되는 바람모델에 관한 상태변수 표현식 및 출력방정식은 식 (14), 식 (15)와 같다.
| (14) |
| (15) |
여기서 Vaυg는 평균 풍속을 나타내며(≈Vw(10)), w2는 평균이 0이고 표준편차가 1인 가우시안 백색잡음프로세스(Gaussian white noise process)를 나타낸다.
바람모델을 통해 출력되는 물리량은 풍속이므로, 이것을 선체측면에 작용하여 발생하는 저항력으로 변환할 필요가 있다. 이에 본 논문에서는 Isherwood가 제안한 환산식을 이용하여 외력을 산출한다. 선박의 횡축으로 작용하는 풍력은 식 (16)과 같다.
| (16) |
여기서 풍력각 γR의 함수 CY(γR)은 힘계수(force coefficient)를 나타내며, ρw는 공기의 밀도를, AL은 수면 상에 노출된 선체에 대한 종방향 단면적을 나타낸다. 한편 CY(90°)에서의 계수 값은 문헌 [6]을 참고하여 Isherwood가 제시한 방법을 토대로 산출하였다.
2.4 기조력 모델
부두에 계류 중인 선박에 있어 또 하나의 주요한 고려 사항으로 조수간만의 차로 인해 발생하는 해수면의 변화와 이로 인해 발생되는 선박의 히브(상하방향) 모션이다. 기조력(tidal force)이 일정한 주기성을 가진다는 것을 고려하여, 본 논문은 기조력에 의해 발생되는 해수면의 시간에 따른 변위를 나타내기 위해 식 (17)의 간단한 모델을 이용한다.
| (17) |
여기서 AT , υT , λT는 각각 파고(wave height), 파속(wave speed), 파장(wave length)를 각각 나타낸다. 식 (17)의 기조력 모델에 의해 발생되는 해수면의 변위(δT)는 식 (10)의 흘수(dw) 변화를 유도하게 되며, 이로 인해 선박의 히브 모션을 구현할 수 있다.
3. 자동계류 기구부의 동적 모델
3.1 기구학 및 속도 기구학
자동계류장치는 선박의 6자유도 운동에 대응하는 구조가 되기 위하여 능동 및 수동 조인트를 가지는 다자유도 의 링크 메커니즘으로 구성될 필요가 있다. 이러한 이유로 자동계류장치는 적절한 회전관절과 직선관절이 조합된 매니퓰레이터 로봇으로 간주될 수 있다. 본 논문에서는 자동계류장치를 간단한 2자유도 매니퓰레이터 로봇으로 가정하고 2차원 평면상의 선박과 매니퓰레이터 로봇의 운동만을 고려하여 제어기를 설계하고자 한다.
Figure 1과 같은 시스템에서 매니퓰레이터 로봇의 각 관절각 변수를 q=(q1,q2)⊤라 하고 로봇 말단부의 좌표를 p=(xr,yr)⊤라 하면, p 는 식(18)로 나타낼 수 있다.
| (18) |
여기서 L1, L2는 각각 링크에 대한 길이를 나타낸다. 매니퓰레이터 자코비안은 관절각속도와 말단부의 속도의 관계를 나타내며 로 나타낼 수 있다. 여기서 자코비안 J는 식 (19)과 같다.
| (19) |
3.2 매니퓰레이터 로봇의 동적 모델
라그랑지안 함수(Lagrangian function)는 운동에너지와 위치에너지의 차를 나타내는 함수로 본 논문에서는 라 표기한다. 또한 일반화좌표(generalized coordinates)와 일반화힘(generalized force)을 각각 q∈Rn, τ∈Rn라 표기할 때 시스템의 동적 모델은 식 (20)의 오일러-라그랑지 방정식(Euler-Lagrange equation)을 통해 유도된다.
| (20) |
식 (20)을 2자유도 매니퓰레이터 로봇에 적용하여 동적 모델을 유도하면 식 (21)과 같다.
| (21) |
여기서 은 질량행렬, 코리올리스 및 원심력, 중력에 대한 항을 각각 나타내고 식 (22 ~ 식 (24)와 같이 유도된다[9].
| (22) |
| (23) |
| (24) |
단, m1과 m2는 각 링크의 질량을 나타내며 L1과 L2는 각 링크의 길이를, g는 중력가속도를 각각 나타낸다.
매니퓰레이터를 이용한 작업 시 각 관절에서 발생하는 추가적인 힘을 고려하여 식 (21)의 동적모델을 다시 쓰면 다음과 같다.
| (25) |
여기서 dr(q)는 액추에이터의 감속기 등에서 발생하는 점성마찰력을 나타내는 감쇠항(damping term)이며, fext는 작업공간에서 매니퓰레이터 말단부에 작용하는 외력을 나타낸다. 본 논문에서는 자동계류장치의 말단부가 선체에 부착된 상황을 가정하였으므로 외력 fext의 주요인자는 선체의 동요로부터 발생하게 된다. 선체의 동요가 바람, 파도, 조류 등의 외란에 의해 발생함을 고려하면, 해상환경의 외란 요소가 선체를 매개체로 하여 매니퓰레이터의 외란으로 전달되고 있는 구조임을 알 수 있다.
3.3 자동계류장치와 선박의 동적 상호작용 모델
자동계류장치와 선박의 동적모델이 서로 연계되기 위해서는 두 시스템 간의 동적 상호작용 모델이 필요하다. 이를 위해 실제 상황을 고려해 보자. 일단 자동계류장치가 선체에 부착하게 되면 외력에 의해 동요되는 선박의 운동력은 계류장치의 말단 흡착부를 거쳐 매니퓰레이터의 각 액추에이터로 전달된다. 일반적으로 매니퓰레이터 말단부에 가해지는 힘을 기반으로 제어기를 구성하는 경우 외력을 계측할 필요가 있으며, 이러한 목적으로 F/T센서(force/torque sensor)가 이용될 수 있다. 본 논문에서는 이러한 상황에 착안하여 동적 상호작용 모델로서 힘센서 모델을 고려한다. 월드좌표계상에서 힘센서는 계류장치 말단부에 부착되어 있으며, xW축과 yW축에 가해지는 외력을 계측할 수 있다고 가정한다. 현재 계류장치 말단부의 위치를 yr∈R2, 말단부가 부착되어 있는 선체표면의 좌표를 ys∈R2라 하면, 두 시스템이 상호작용하는 과정에서 발생하는 미소변위를 ∆y=yr-ys이라 표현할 수 있다. 계류장치 말단부에서 계측되는 외력은 식 (23)과 같이 추정될 수 있다.
| (26) |
여기서 K=diag(kx,ky)는 xW축, yW축 에 대한 강성계수(stiffness coefficient)가 각각 대각요소로 구성되는 대각행렬(diagonal matrix)이다. 이렇게 외력 추정치 가 산출되면 계류 장치는 이를 기반으로 제어를 수행하게 되는데, 이때 관절 토크 제어입력 τr이 계산된다. 또한 관절 토크 τr로부터 J-⊤τr의 관계식을 통해 작업공간에서의 작용 힘으로 변환된다. 이 힘은 작업공간에서 계류 중인 선박에 작용하는 풍력 외란(τwind)과 더불어 계류 장치로부터 발생되는 또 다른 외란으로 작용한다. 이를 수식으로 나타내면 식 (27)와 같다.
| (27) |
여기서 gr(q)는 매니퓰레이터 동적모델의 중력 항을 나타낸다. 식 (27)의 매니퓰레이터 외력 항에서 중력 항이 차감된 이유는 다음과 같다. 매니퓰레이터 말단부의 위치를 제어하는 경우 중력보상을 의한 추가적인 토크 발생이 필요하지만, 선체의 입장에서 본다면 이 중력보상 토크가 외력으로 직접 작용하지 않기 때문이다.
4. 제어기 설계
4.1 제어기 설계
관절각 변수 q=(q1,q2)⊤로 구성된 매니퓰레이터의 동적 모델에서 외부에서 가해지는 모든 외력을 외란으로 간주하여 τd 라 표기하자. 또한 항을 제외한 나머지 항 모두를 합하여 이라 하면 식 (25)는 식(28)과 같이 다시 정리할 수 있다.
| (28) |
매니퓰레이터를 이용하여 선박을 원하는 지점에 계류하기 위해서는 매니퓰레이터 말단에서의 위치를 고려하여야 한다. 이에 작업공간에서의 위치는 식 (18)로부터 식 (29) ~ 식 (31)과 같이 나타낼 수 있다.
| (29) |
| (30) |
| (31) |
식 (28)로부터의 를 이용하면 식 (31)의 는 식 (32)와 같이 정리된다.
| (32) |
식 (32)에 u, υ를 각각 로 치환하면 식 (33)과 같이 간략화 된다.
| (33) |
식 (33)은 로봇매니퓰레이터를 작업공간에서 선형화한 결과로 해석할 수 있다. 식 (33)으로부터 새로운 제어입력 u(t)로 매니퓰레이터 말단의 위치를 제어할 수 있고, u와 기존의 제어입력 τr와의 관계는 식 (34)와 같다.
| (34) |
4.2 슬라이딩모드 제어기 설계
슬라이딩 모드 제어기의 설계[10]를 위해 상태변수 벡터 x1,x2를 도입하여 x1=p=(xr,yr)⊤, 로 정의하자. 그러면 매니퓰레이터 작업공간에서의 거동을 표현하는 식 (33)은 식 (35)와 같은 상태방정식으로 다시 표현할 수 있다.
| (35) |
매니퓰레이터의 말단의 위치 p를 목적으로 하는 위치 pd로 제어하기 위해 오차함수를 식 (36)과 같이 정의한다.
| (36) |
아울러 식 (36)의 오차함수를 고려한 스위칭함수를 식 (37)과 같이 설정한다.
| (37) |
스위칭함수로 구성된 리아프노프함수 후보를 식 (38)과 같이 선정하고 식 (38)에 대한 시간미분과 식 (30), 식 (33), 식 (36)을 이용하면 식 (39)과 같이 정리된다.
| (38) |
| (39) |
식 (39)에서의 제어입력 u를 다음과 같이 설정한다.
| (40) |
여기서 υ는 작업공간에서 매니퓰레이터의 말단부에 작용하는 xR축 및 yR축의 외란성분으로 구성된 외란벡터를 나타낸다. 식 (40)을 이용하여 식 (39)를 정리하면 식 (41)의 부등식이 성립함을 알 수 있다.
| (41) |
따라서 식 (38)의 함수 V는 리아프노프 함수가 되고 이를 통해 σ=0이 얻어진다. 스위칭함수(σ(t))가 0이 되면 식 (36)의 오차함수에 대한 정의로부터 e(t)→0, t→∞가 달성되는 것을 알 수 있다. 즉, 식 (40)의 슬라이딩 모드제어기를 적용하여 매니퓰레이터의 말단 위치를 원하고자 하는 위치로 이동(p→pd)시킬 수 있다.
본 논문에서는 로봇의 말단부에 F/T센서를 탑재한 것으로 가정하였다. 말단부가 선체에 접촉된 상태에서 F/T센서로부터 측정되는 대부분의 힘은 선체와의 상호작용 과정에서 발생된다. 따라서 본 논문에서는 외란벡터 υ의 추정치로서 식 (26)의 를 이용한다. 한편 본 논문에서 다루는 슬라이딩 모드 제어기는 위치제어를 목적으로 설계되었다. 자동계류시스템에 의해 계류 중인 선박에 있어 횡축에 대한 위치 제어는 필요하지만 종축에 대한 위치는 상황에 따라 조정될 필요가 있다. 이는 기조력 등으로 인해 발생하는 흘수의 변화가 있기 때문이다. 식 (26)의 에 대한 yW축 요소를 라 하면 로 풀어 쓸 수 있으며, 이를 yd에 관해 다시 풀면 를 유도할 수 있다. 본 논문에서는 이 관계식을 통해 F/T센서로부터 추정된 외력을 이용하여 yW축에 대한 목표위치를 산출하여 pd를 식 (42)와 같이 구성한다.
| (42) |
여기서 xd는 xW축에 대한 목표위치를 나타내며 kf는 ky에 대응되는 가중치를 나타낸다.
5. 시뮬레이션 결과
5.1 시뮬레이션 환경
본 논문에서는 자율운항선박이 자동계류장치를 이용하여 계류된 상황에서, 바람 및 기조력으로 인해 동요하는 선박을 자동계류장치를 통해 안정화시키기 위한 제어기법을 다루고 있다. 시뮬레이션은 자동계류장치의 말단부가 Figure 1에 나타난 바와 같이 선체 측면에 부착된 상태에서 수행된다.
시뮬레이션에 이용되는 선박의 주요한 파라미터는 00호의 선박에 대한 제원을 토대로 설정되었다. 다만 직접적으로 구할 수 없거나(예: 선체질량) 근사과정에서 오차가 발생하는 경우 등에 관해서는 이를 보상하기 위한 근사 수치를 이용하였다. 시뮬레이션에 이용된 선박 파라미터는 Table 1과 같다.
자동계류장치는 아직 국내에 보급되어 항만부두에 설치된 사례가 없다. 더불어 현존 계류장치의 세부 제원에 대한 정보를 찾기가 쉽지 않은 관계로, 본 논문에서는 대상 선박의 규모를 고려하여 파라미터 값들을 임의로 설정하였다. 일예로 자동계류장치의 첫 번째 링크에 대한 질량은 두께 5mm 스테인리스 재질의 사각 빔(300 × 300mm)으로 제작되었음을 가정하여 산출된 값을 이용하였다. 자동계류장치의 시뮬레이션을 위한 각 파라미터들은 Table 2와 같다.
5.2 결과 및 고찰
바람에 의한 선체의 동요 정도를 파악하기 위해 식 (6)의 선체 동역학 모델과 식 (14), 식 (15)의 바람 모델에 대한 시뮬레이션을 수행하였다. 시뮬레이션 프로그램은 MATLAB환경에서 구현되었고, 상태방정식의 해를 구하기 위해 Runge-Kutta 4차 수치적분 방법이 이용되었다. 시뮬레이션 초기 조건으로 선박의 상태변수를 η=(0,4.9962,0)⊤, ν=(0,0,0)⊤으로 설정하였다. 식 (14)-(15)의 바람 모델에 대해서는 평균 풍속 Vaυg를 초기 5m/s(9.72knots)에서 시작하여 10초 동안 유지한 후 0.2m/s가 되도록 설정하여, 돌풍이 불어 선박에 외력을 가하는 상황을 모사하였다. 식 (17)의 기조력 모델에 대해서는 파고, 파속, 파장을 각각 0.5m,10m/s, 100m로 설정하였다. 기조력 에 있어 실제 조석주기를 적용하는 경우 모의실험 시 흘수의 변화가 너무 미미하므로 조석주기는 10초로 설정하였다.
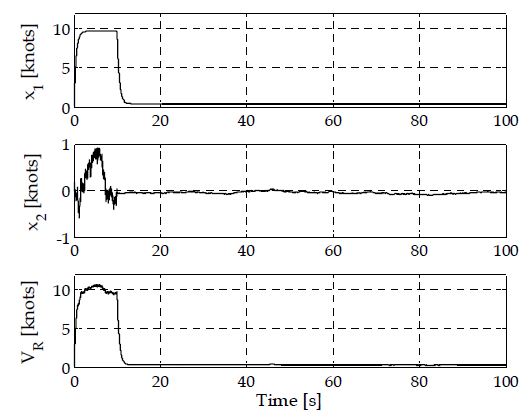
Figure 2는 시간에 따른 바람 모델 요소의 상태 변화를 나타내고 있다. 상단 첫 번째 그래프는 식 (14)의 평균 풍속(x1)에 대한 상태 변화를 나타내며, 가운데 그래프는 x2의 상태 변화를 각각 나타내고 있다. 최 하단의 그래프는 2개의 상태가 합성된 최종 풍속 출력(VR)을 나타내고 있다.
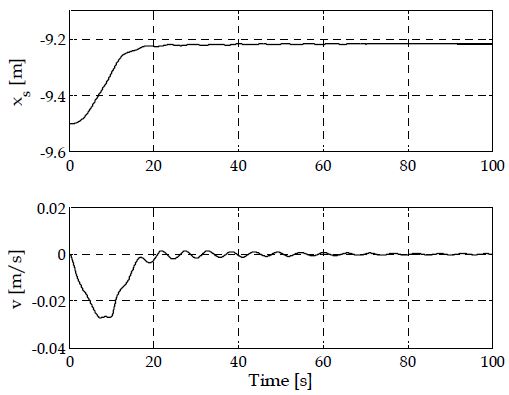
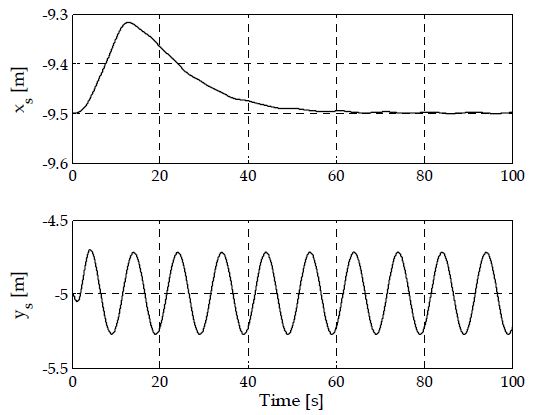
Figure 3~Figure 5는 바람 외력에 따른 선박의 거동을 나타내는 도표이다. Figure 3은 월드좌표계를 기준으로 선박의 횡축 모션을 나타낸 것이며, 이는 각각 xW축 상의 선박 중심 위치(xs)와 이에 대응되는 선박고정좌표계 상의 속도(υ)를 나타낸다. 그림에서 나타난 바와 같이 Figure 2의 바람 외란에 의해 선박은 초기 위치 –9.5m에서 우측 방향으로 대략 27cm가량 밀려감을 알 수 있다. 10초 이후에는 외란의 영향이 크지 않으므로 밀려난 상태를 유지하고 있다.
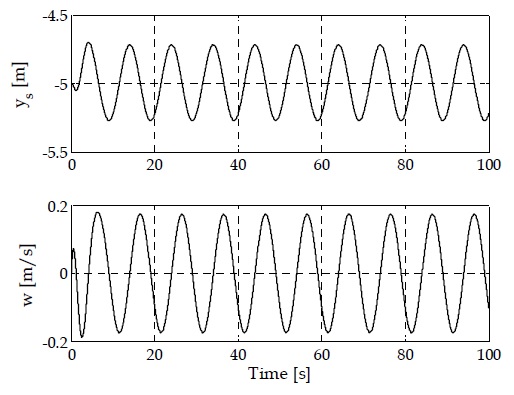
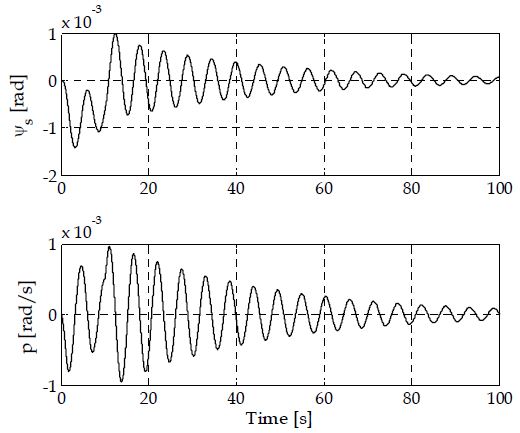
Figure 4는 선박의 종방향 모션의 시간에 따른 변화를 나타낸 것으로, 월드좌표계상의 yW축에 대한 선박 중심 좌표(ys)와 속도(w)를 각각 나타낸다. 선박의 종방향 모션은 주로 기조력으로 인한 선박의 흘수변화에 기인한 것으로 지속적으로 진동하고 있음을 알 수 있다. Figure 5는 선박의 롤축(roll-axis)에 대한 각도 및 각속도의 시간변화를 나타내고 있다. 바람 및 기조력에 의한 영향으로 선체의 롤 모션이 발생하고, 점진직으로 이러한 모션이 감쇠하고 있음을 알 수 있다.
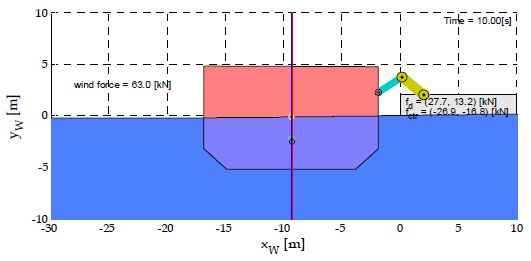
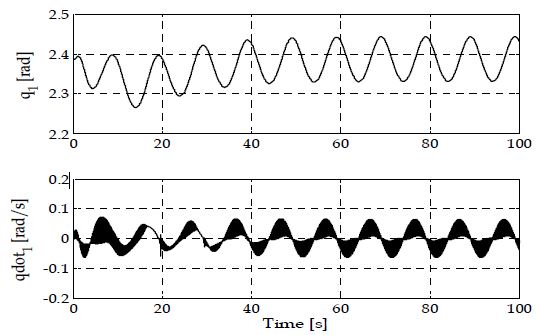
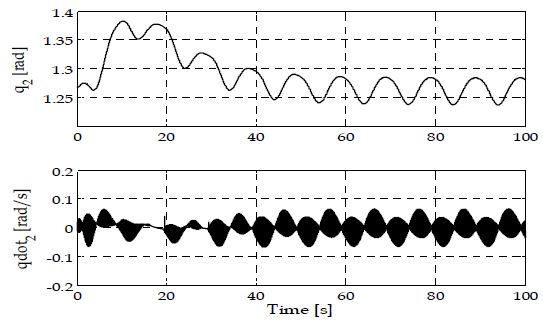
본 절에서는 자동계류장치에 의해 계류 중인 선박에 외란이 가해지는 경우 제안된 제어기의 안정화 성능에 관해 살펴본다. 자동계류장치의 베이스인 로봇좌표계 {R}은 월드좌표계를 기준으로 (2,2)[m]에 위치시켰고, 계류장치의 말단부는 (-2,2.5)[m]에 위치하도록 설정하였다. 이때 말단부의 흡착패드는 선체에 흡착된 채로 고정되어 있다고 가정하였다. 이러한 설정아래 5.2.1절에서의 외란 조건(바람 및 기조력)을 동일하게 인가하여 100초 동안 시뮬레이션을 수행하였다. Figure 6은 MATLAB 환경에서 수행되고 있는 시뮬레이션의 한 장면(10초 경과 시점)을 나타내고 있다. Figure 7과 Figure 8은 계류장치 매니퓰레이터의 각 관절에 대한 각도(q1, q2)와 각속도()의 시간에 따른 변화를 나타내고 있다. 관절각 q1과 q2 모두 지속적인 진동 패턴을 보이는데, 이는 기조력에 의한 흘수 변화로 인해 선체의 종방향 운동이 발생하며 계류장치가 그 변위에 대한 추종제어를 수행함으로써 나타나는 결과이다. 특히 q2는 두 번째 링크에 대한 관절각으로 초기 10초 동안 최대변위를 보이는데 바람에 의한 선체의 횡방향 운동에 의한 것임을 알 수 있다. 두 관절의 각속도의 경우 스위칭 현상이 발생하고 있는 것을 관찰할 수 있는데, 이 구간에서 슬라이딩모드 제어기가 슬라이딩 표면(sliding surface)에 진입하여 동작하고 있음을 보여주고 있다.
Figure 9는 로봇의 작업공간에서 매니퓰레이터 말단부의 xR축 위치오차(ex), 제어력(fx), 외력(fextx)을 각각 나타낸다. 제어력 fx는 액추에이터의 관절 토크 입력(τr)이 작업 공간상에 변환된 힘의 xR축 요소이다. 외력 fextx는 식 (26)의 힘 센서 모델로부터 발생되는 힘으로, 초기 50초까지의 주요 요인은 바람 외란에 의해, 그 이후는 선체의 흘수변화에 의한 영향이라 볼 수 있다. Figure 9에서 오차 ex의 거동을 통해 알 수 있듯이 복합적인 외란이 작용하더라도 제안된 슬라이딩모드 제어기는 선박이 목표위치로 점진적으로 이동되도록 제어하고 있음을 알 수 있다.
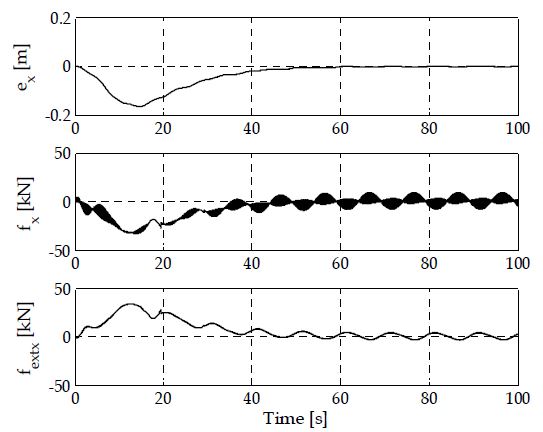
Position errors, control forces, and external forces of automatic mooring device in xR -axis in task space
Figure 10은 yR축에 대한 말단부의 위치오차(ey), 제어력(fy), 외력(fexty)의 시간에 따른 변화를 나타내고 있다. 여기서 말단부의 위치오차가 0에 근접하고 있는 것은 슬라이딩모드 제어기가 yR축에 대해 잘 추종하고 있음을 나타낸다. 반면 제어력 fy는 지속적으로 작용하고 있는데, 이는 선체가 흘수변화로 종방향 운동을 수행하고 이로 인해 매니퓰레이터의 말단부에 지속적인 외력 fexty이 발생되기 때문이다.
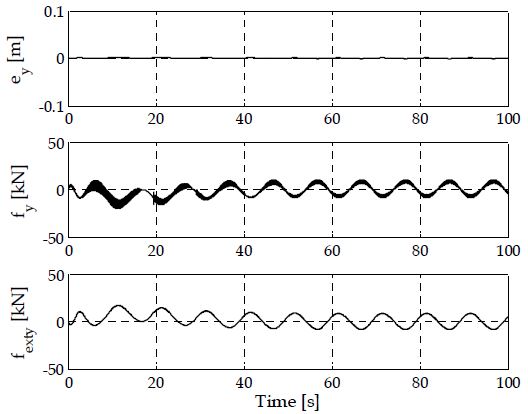
Position errors, control forces, and external forces of automatic mooring device in yR -axis in task space
자동계류장치의 목적은 외란이 있는 상황에서 선박의 동요를 억제하고 정해진 계류위치를 유지시키는 것이다. Figure 11은 월드좌표계에서 묘사되는 선박의 중심 좌표의 시간에 따른 변화를 나타내고 있다. 선박이 계류된 상황에서 바람외란으로 19cm 가량 xW축 방향으로 밀려나간 후 60초 이후에는 원위치로 복귀되고 있음을 확인할 수 있다. 동시에 yW축의 대해 흘수변화로 인한 지속적인 진동패턴을 유지하고 있음을 알 수 있다. 이것은 자동계류시스템이 선체의 종방향 운동에는 수동적으로 작용하는 반면, 횡방향 운동에 대해서는 능동적인 제어을 수행하고 있음을 의미한다. 이는 본 논문에서 제안된 제어시스템이 외란이 있는 환경에서도 선박을 안정적으로 계류시킬 수 있음을 시사한다.
6. 결 론
본 논문은 자율운항선박이 부두에 접안하는 상황을 고려하여 인간의 개입 없이 자동적으로 계류작업을 수행할 수 있는 자동계류시스템을 다루었다. 이를 위해 우선 복합적인 외란이 있는 선박의 동역학적 운동 특성을 분석하기 위한 시뮬레이션 환경을 제시하였다. 또한 2자유도 매니퓰레이터의 동적 모델 및 선박과의 상호작용 모델을 통한 자동계류 메커니즘을 제안하였다. 특히 본 논문은 선박이 계류된 상황을 고려하여 외란에 강인한 슬라이딩모드 기반의 위치제어 시스템을 설계하였다. 제안된 시스템은 바람으로 인한 횡방향 외란과 기조력에 의한 종방향 외란이 복합적으로 주어진 상황을 고려한 시뮬레이션을 통해 평가되었고, 그 결과 선박의 계류 위치를 안정적으로 유지시킬 수 있었다. 본 논문에서는 자동계류장치의 제어시스템을 설계하기 위하여 3자유도의 선박모델 및 2자유도의 매니퓰레이터 모델에 기반 하였다. 두 시스템의 보다 정확한 거동을 분석하기 위해서는 6자유도의 모델을 다룰 필요가 있으며 이는 추후과제로 남긴다.
Acknowledgments
이 논문은 2017년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(NRF-2015R1C1A1A01053126).
Author Contributions
Conceptualization, H. H. Kim and T. K. Nam; Methodology, H. H. Kim and T. K. Nam; Software, H. H. Kim and J. M Kim; Validation, J. M. Kim and T. K. Nam; Writing—Original Draft Preparation, H. H. Kim; Writing—Review & Editing, J. M. Kim and T. K Nam; Supervision, T. K. Nam;
References
- Cavotec Home Page, http://www.cavotec.com, , Accessed October 21, 2019.
- MoorMaster, https://www.scribd.com/document/69999648/moormaster-aj, , Accessed October 21, 2019.
- MoorMaster Automated Mooring, https://suppliers.porttechnology.org/wp-content/uploads/moormaster-automated-mooring-may-2011.pdf, , Accessed October 21, 2019.
-
E. D. A. Ortega, C. P. B. Blanco, L. Ruiz, and J. Oria, “Empirical analysis of the implantation of an automatic mooring system in a commercial port. Application to the port of santander (Spain),” Maritime Technology and Engineering III: Proceedings of the 3rd International Conference on Maritime Technology and Engineering, pp. 193-200, 2016.
[https://doi.org/10.1201/b21890-28]

-
W. V. D. Molen, D. Scott, D. Taylor, and T. Elliott, “Improvement of mooring configurations in Geraldton Harbour,” Journal of Marine Science and Engineering, vol. 4, no. 1, pp. 3-23, 2016.
[https://doi.org/10.3390/jmse4010003]

-
Y. Y. Kim, K..J. Choi, H. Chung, S. Han, and P. S. Lee, “A ship-to-ship automatic docking system for ocean cargo transfer,” Journal of Marine Science and Technology, vol. 19, no. 4, pp. 360-375, 2014.
[https://doi.org/10.1007/s00773-014-0256-3]

- T. I. Fossen, Guidance and Control of Ocean Vehicles, John Wiley & Sons, 1994.
-
T. I. Fossen, Handbook of Marine Craft Hydrodynamics and Motion Control, Wiley, 2011.
[https://doi.org/10.1002/9781119994138]

- K. M. Lynch and F. C. Park, Modern Robotics, Cambridge University Press, 2017.
-
V. I. Utkin, “Sliding mode control design principles and application to electric drives,” IEEE Transactions on Industrial Electronics, vol. 40, no. 1, pp. 23-35, 1993.
[https://doi.org/10.1109/41.184818]