CFD를 이용한 림추진기의 받음각 최적화에 대한 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
최근 선박으로부터 배출되는 대기오염물질에 대한 규제 강화에 따라 전기추진선박과 전기추진선박용 림추진기에 대한 관심이 고조되고 있다. 림추진기는 고전적인 추진기와는 다른 유동특성을 가지므로 림추진기가 가지는 고유한 유동특성을 반영하여 기초설계한 림추진기를 최적화할 필요가 있다. 본 연구는 기초설계한 림추진기에 대한 최적화에 대한 연구이며, 본 연구에서는 hub-less 림추진기를 CFD를 이용하여 받음각을 최적화하는 시행착오의 방법을 제시하였다. CFD를 통한 성능분석 결과, 본 연구에서 제시한 최적화 방법은 효율의 상승 및 캐비테이션의 저감에 효과가 있음을 알 수 있었다. 향후 림추진기에 대한 다양한 형상 파라미터에 대한 최적화 연구를 진행할 예정이다.
Abstract
Currently, interest in electric propulsion vessels and rim-driven propellers (RDPs) is increasing due to strict regulations on air pollution materials emitted from ships. Because an RDP has different flow characteristics than those of a conventional propeller, optimizing the fundamental design of an RDP to reflect its inherent flow characteristics is necessary. This study is on the optimization of an RDP. Specifically, we present a method of trial and error to optimize the angle of attack using computational fluid dynamics (CFD) for a hubless RDP. Results of performance analysis through CFD revealed that the optimization method proposed in this study was effective at increasing RDP efficiency and reducing cavitation. In the future, we intend to conduct further optimization studies on various parameters for RDPs.
Keywords:
Hubless rim-driven propeller, Optimization method, Computational fluid dynamics키워드:
허브리스 림추진기, 최적화 방법, 전산유체역학1. 서 론
선박으로부터 배출되는 대기오염물질에 대한 규제 강화에 따라, 전기모터로 추진기를 구동하는 고효율 전기추진선박과 전기모터와 추진기를 일체형으로 제작이 가능한 hub-less 림추진기(or shaft-less rim-driven propeller, 이하 RDP)에 대한 관심이 고조되고 있다.
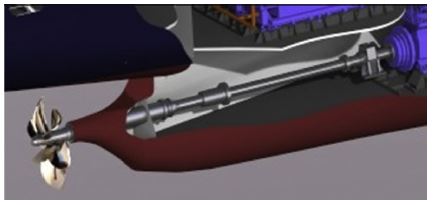
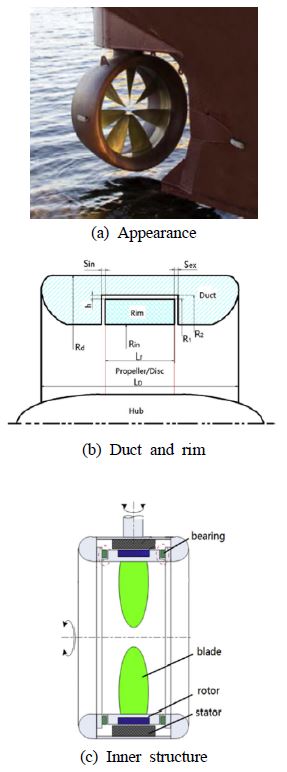
전통적인 스크류 추진기(Figure 1)는 축과 허브를 가지며 허브로부터 반경방향으로 추진기의 날개가 배치된다. 그러나 hub-less 림추진기(Figure 2)는 모터의 고정자와 영구자석이 덕트 내에 설치되고 덕트의 림(rim)에서 추진기 중심축 근방까지 추진기의 날개가 배치된다[1]. 전통적인 스크류 추진기와 비교하여 hub-less 추진기는 소음과 진동의 저감, 고효율, 설치의 유연성, 가볍고 소형이라는 점 등의 많은 장점을 가진다[2].
최근 독일의 Voith 사, 노르웨이의 Brunvoll 사, 네덜란드의 Van Der Velden Marine 사가 hub-less 추진기를 개발하였으나, 그 역사가 짧아 hub-less 림추진기에 대한 연구는 소수에 불과하다[2].
Hub-less 림추진기에 대한 연구는 크게 두 가지로 분류할 수 있다. 첫째는 hub-less 림추진기에 대한 기초설계에 대한 다수의 연구들이다[1][3]-[6]. 전통적인 추진기의 설계이론 혹은 그 성능곡선을 참고하여 피치비가 일정한 림추진기를 설계하거나 림추진기 전체 깃에 걸쳐 축방향 유속이 일정한 것으로 가정하고 림추진기를 설계한 연구가 hub-less 림추진기의 기초설계에 대한 연구에 해당한다.
둘째는 상기와 같이 기초 설계한 추진기 형상을 보다 최적화하여 림추진기의 효율을 향상시킨 극소수의 연구들이다[7][8]. 전통적인 스크류 추진기는 추진기 팁(반경비 r/R이 1.0인 위치)에서 절대속도에 대한 선회(swirl) 성분이 최소이다. 그러나 Q. M. Cao et al. [8]가 지적한 바와 같이 림추진기는 림의 회전운동으로 인하여 반경비 1.0인 위치에서 절대속도에 대한 선회 성분은 최대이다. 이와 같은 차이로 인하여 전통적인 스크류 추진기의 설계이론을 토대로 기초설계한 림추진기는 최적화 되어야 한다. 구체적인 연구사례로 A. J. Dubas[7]는 최적화를 통하여 기존 림추진기 대비, 최대 6% 효율을 상승시켰다.
Hub-less 림추진기는 덕트유기속도, 허브의 부재 등으로 인하여 추진기 반경에 따라 속도장이 불균일하다[8]. 그러므로 림추진기의 최적화에서 가장 중요한 파라미터는 반경비에 따른 피치비이며[2], 기초설계한 hub-less 림추진기는 반경위치에 따른 불균일한 속도장을 반영하여 피치비를 변경할 필요가 있다. 반경비에 따라 피치비를 림추진기의 속도장을 토대로 변경한다는 것은 깃의 받음각(angle of attack)을 속도장에 적합하도록 변경한다는 것을 의미한다.
본 연구는 기초설계한 hub-less 림추진기의 최적화에 대한 것으로 주요 최적화 파라미터는 기초설계한 hub-less 림추진기의 받음각이다. 본 연구는 CFD 해석결과를 토대로 림추진기의 받음각을 최적화하는 시행착오의 방법(Method of trial and error)을 제시하고 본 연구에서 제시한 최적화의 효과에 대해서 살펴보았다.
2. 최적화 절차
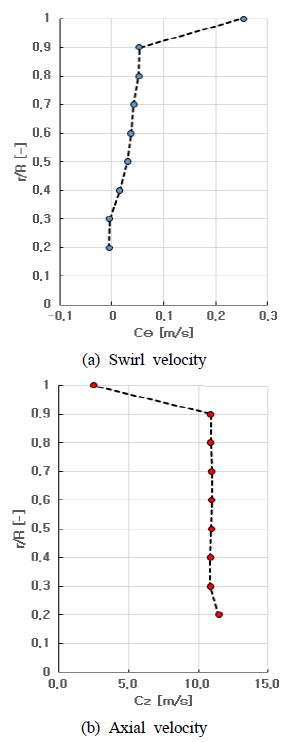
최근 D. Y. Kim et al. [1]은 추진기 전체 반경에서 축방향의 유속이 일정한 것으로 가정하고 워터제트와 축류펌프의 설계이론을 토대로 hub-less 림추진기에 대한 기초설계를 수행하였다. D. Y. Kim et al. [1]이 기초설계한 림추진기에 대한 CFD 해석결과로부터 반경에 따른 절대속도의 선회 성분과 축방향 성분을 나타내면 Figure 3과 같다. 추진기 외륜에 위치한 림의 회전운동에 따라 1.0R(림과 추진기가 접하는 위치)의 선회 속도성분은 최대가 되는 반면(Figure 3 (a)), 점성효과에 의해 1.0R의 축방향 속도성분은 최소가 된다(Figure 3 (b)).
Figure 3을 토대로 반경비에 따른 절대속도의 유동각과 D. Y. Kim et al. [1]이 설정한 깃의 각도를 비교하여 받음각을 산출하면 Table 1과 같다. D. Y. Kim et al. [1]은 추진기의 축방향 유속이 일정한 것으로 가정하고 받음각이 전체 반경에 있어 2.5 도(degrees)가 되도록 추진기를 설계하였으나 Table 1과 같이 기초설계한 림추진기의 받음각은 반경 위치에 따라 대단히 상이한 것을 알 수 있다. 이것은 Q. M. Cao et al. [8]가 지적한 바와 같이 림추진기를 유동 방향에 적합하도록 최적화 하여야 한다는 것을 의미한다. 특히, Table 1의 받음각이 음수인 영역은 유체가 흡입면을 향하고 있다는 것과 이 영역은 효과적으로 추력을 형성하고 있지 못한다는 것을 의미하므로 반드시 최적화가 되어야 할 부분이다.
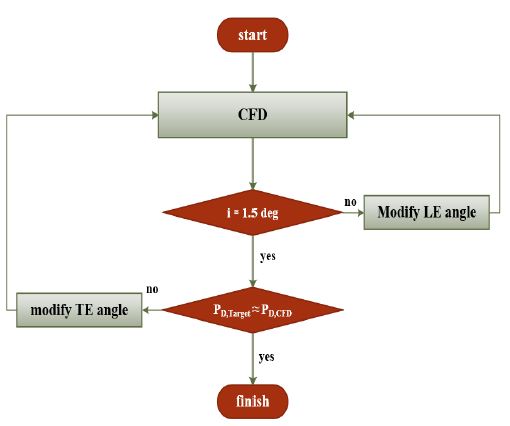
본 연구에서 수행한 받음각의 최적화 과정은 Figure 4와 같다. 우선, 기초설계한 hub-less 림추진기에 대한 CFD를 수행하고 그 결과로부터 받음각을 분석하였다. 본 연구에서 기준으로 하는 림추진기는 D. Y. Kim et al. [1]이 기초설계한 hub-less 림추진기이다. 이 림추진기는 기초설계 당시에는 받음각을 2.5 도로 설정하였으나, CFD 결과 캐비테이션을 완벽하게 제거하지 못하였다. 캐비테이션은 받음각을 감소시켜 개선할 수 있는 부분이므로 CFD를 이용하여 분석된 절대속도의 유동각으로부터 받음각이 1.5 도가 되도록 깃의 앞날(LE; leading edge) 각도를 수정하여 CFD를 재차 수행하였다. 만약 CFD 결과로부터 받음각이 1.5 도와 근사하다면, 설계목표 출력과 받음각을 수정한 림추진기의 출력을 비교하고 설계목표 출력과 림추진기의 출력이 근사하도록 깃의 뒷날(TE; Trailing edge) 각도를 수정하였다. 앞날각도(혹은 받음각)를 수정할 경우 깃에 의한 유동의 편향각 증감으로 인하여 림추진기의 출력이 증감하기 때문에 추가적으로 뒷날 각도를 수정하는 것은 최적화한 림추진기의 출력을 목표출력과 근사하게 유지시키기 위한 조치이다. 상기의 과정은 경우에 따라 수차례 반복될 수 있겠으나, 본 연구의 경우 7차례의 재설계를 통하여 출력을 근사하게 유지하면서 림추진기의 1.0R을 제외한 반경위치에서 약 1.5의 받음각을 갖는 림추진기 형상을 얻을 수 있었다.
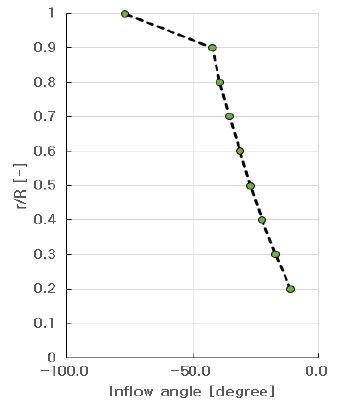
Table 1에서 보인 α1,CFD을 그래프로 표현하면 Figure 5와 같다. 0.2R에서 0.9R까지 유동각도는 –43도 이상이고 반경비에 따라 유동각도는 거의 선형적으로 변화하고 있으나 1.0R의 유동각도는 약 –77도로 그 외 반경위치의 유동각도와는 크게 상이하다. 이것은 림의 회전운동과 유체의 점섬효과로부터 기인한 것으로 림 추진기의 고유한 유동특징이다. 추진기의 모델링과 앞날 및 뒷날 각도 조정은 D. Y. Kim et al. [1]의 연구와 같이 ANSYS사의 BladeGen V13.0을 사용하였고, Figure 5의 가공하지 않은 유동각도를 토대로 하여 BladeGen을 이용하여 추진기를 모델링한 경우 1.0R에서 급격한 앞날의 각도 변화로 추진기 모델링에 실패하였다.
이에 따라, 본 연구에서는 Figure 4에 의해 결정된 0.2R에서 0.9R까지의 앞날 각도를 토대로 Matlab R2016a를 이용하여 반경위치에 따른 앞날 각도에 대한 3차 다항식을 정의하고, 이 3차 다항식의 1.0R에 대한 외삽값을 이용하여 1.0R의 앞날 각도를 반복적으로 결정하였다.
D. Y. Kim et al. [1]이 기초설계한 림추진기를 토대로 전술한 최적화 과정을 거친 최종 케이스는 Opt7에 해당한다.
3. 성능분석
3.1 모델링
Opt7 케이스의 림추진기와 기초설계한 림추진기는 동일하게 덕트 형상을 갖는다[1]. 또한, 두 림추진기는 동일한 축방향 코드길이와 날개 개수를 가진다. 최적화에 따른 림추진기의 유일한 변화는 프로펠러 입구와 출구의 깃 각도이다. Table 2는 기초설계한 림추진기와 받음각을 최적화한 림추진기(Opt7)의 깃 각도를 비교한 것이다.
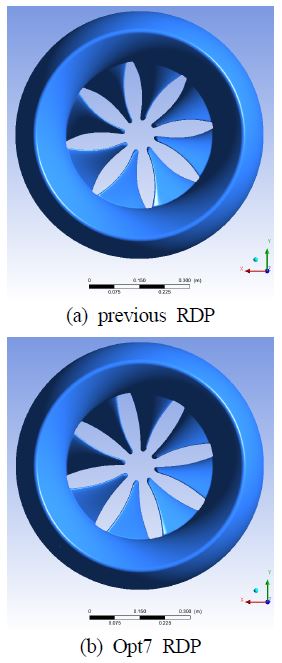
림추진기의 모델링에는 Ansys BladeGen 13.0을 이용하였으며, Figure 6은 기초설계한 림추진기(previous RDP)와 최적화한 림추진기(Opt7 RDP)의 최종형상을 비교한 것으로 깃 각도의 변화는 림추진기의 프로펠러에 대한 투영면적의 변화를 초래하였다.
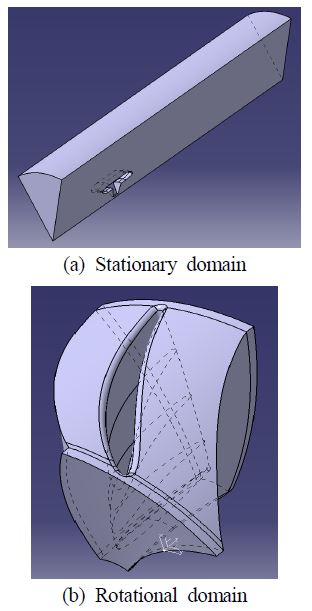
Figure 7은 Figure 6 (b)을 토대로 CATIA V5를 이용하여 단일유로(추진기 날개 개수가 8개이므로 단일유로에서 고려된 각도는 45 도 임)에 대하여 모델링을 수행한 결과이다. 림추진기의 덕트 외경은 740 mm 이며 이를 기준으로 상류 방향으로 2.5배, 하류 방향으로 7배, 반경방향으로 3배의 유동 영역을 모델링하였다. Opt7의 검사체적 크기를 선정한 파라미터는 기초설계한 림추진기의 성능분석에 이용된 파라미터와 동일하다.
3.2 격자형성
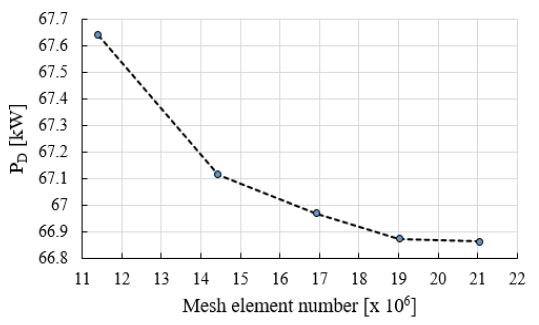
Figure 7의 비회전 도메인과 회전 도메인에 Ansys Meshing V13.0을 이용하여 비정렬격자와 프리즘을 형성하였다. 전달동력을 기준하여 격자 의존성 점검을 수행하였으며, 격자 의존성 점검 결과는 Figure 8과 같다. 격자의존성 점검결과, 비회전 도메인과 회전 도메인에 형성된 격자 수는 Table 3과 같이 총 약 2,100 만개이다. 최종격자의 max. y+는 19.81로 수치해석에 사용된 SST 난류모델의 권장범위를 만족한다.
3.3 수치해석모델
Opt7의 성능을 분석하기 위하여 수치해석을 수행하였으며, 수치해석에 이용한 상용 수치해석 프로그램은 ANSYS CFX 13.0이다. 기초설계한 림추진기의 설계조건(Table 4)과 같이 입구조건으로는 전진속도인 3.91 m/s와 난류강도 5%가 사용되었다. 출구 조건으로는 추진기 설치 위치를 고려하여 107.325 kPa이 사용되었으며 회전도메인의 회전수는 설계조건과 동일하게 상용출력(NCR) 조건에는 483 rpm, 그리고 최대출력(MCR) 조건에는 500 rpm으로 설정되었다. 고정도메인의 외주면은 open 경계조건이 사용되었으며, open 경계는 출구조건과 같은 압력을 설정하였다. 각 인터페이스에는 주기 조건과 frozen rotor 모델을 설정하였다.
3.4 설계조건에 대한 수치해석결과
격자 의존성 점검을 마치고 y+ 값을 규정 범위 내로 규제한 Opt7의 출력, 효율과 같은 성능을 살펴보기 이전에 Opt7의 받음각에 대하여 최적화가 적절하게 이루어졌는지 살펴보겠다. Table 5는 최적화 과정을 거친 Opt7의 받음각을 분석한 결과이다. Figure 4에서 보인 바와 같이 본 연구에서는 받음각의 최적화를 1.5 도 기준으로 하였으며, Opt7은1.0R 위치를 제외한 나머지 반경위치에서 받음각에 대한 최적화가 이루어졌음을 알 수 있다. 특히, 유체가 비정상적으로 흡입면을 향하는 것을 의미하는 영역(받음각이 음수인 영역)이 완벽하게 제거하였음에 주목할 필요가 있다.
상용출력(NCR)과 최대출력조건(MCR)에서 Opt7의 성능은 Table 6과 같으며, 기초설계를 수행하였던 림추진기의 NCR과 MCR에 해당하는 성능은 Table 7과 같다. Table 6과 Table 7의 비교로부터 전달동력(PD)은 거의 일정하게 유지되었음을 알 수 있다. 또한, 받음각의 최적화에 의해 설계조건(NCR 및 MCR 회전수)에서 약 0.4%의 효율 상승을 기대할 수 있음을 알 수 있다. 즉, 이것은 림추진기의 불균일한 유동특성을 반영하여 받음각를 최적화할 경우 림추진기의 효율을 상승시킬 수 있음을 의미한다.
한편, 기초설계한 림추진기는 캐비테이션을 제거하기 위하여 많은 노력을 했음에도 불구하고 흡입면의 캐비테이션을 완벽하게 제거하지 못하였다. 이에 따라 본 연구에서는 받음각을 1.5 도로, 기초설계에 적용한 받음각 2.5 도와 비교하여 낮은 받음각을 설정하고 최적화하였다. 그러므로 캐비테이션의 측면에서 받음각 변화 및 최적화의 효과에 대하여 알아볼 필요가 있다.
Table 8은 Table 1의 기초설계한 림추진기의 받음각과 Table 5의 최적화한 림추진기의 받음각을 비교한 것이다. 일반적으로 반경방향의 유동을 무시할 수 있어 특정 반경에서 유동특성이 2차원적이라면 받음각의 증가는 캐비테이션 정도를 증가시킨다[9]. 최적화에 의해 받음각이 증가된 반경 위치는 Table 8에서 붉은색으로 강조하였다. 최적화 과정에서 받음각을 2.5 도에서 1.5 도로 감소시키기는 하였으나 최적화를 통하여 0.6R에서 1.0R에 이르는 영역은 오히려 받음각이 증가되었다. 일반적인 통념에 의하면 받음각이 증가된 영역에서는 캐비테이션이 증가되는 경향을 보이는 것이 정상일 것이다.
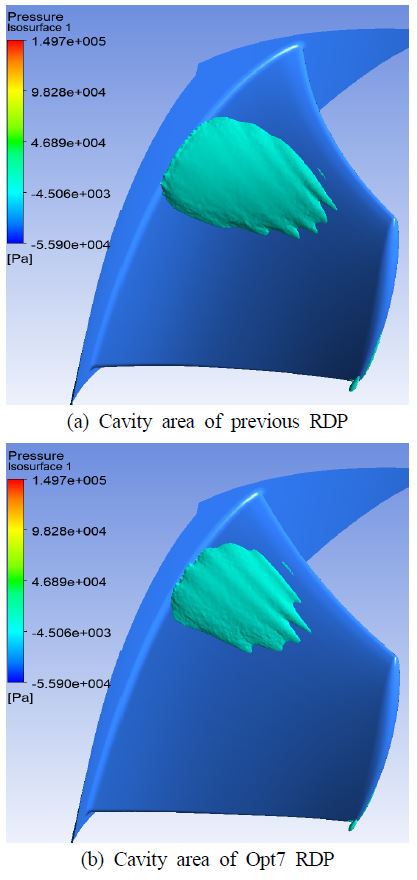
일반적으로 추진기의 캐비테이션 영역은 절대압 3.0 kPa 이하로 간주되고 있으며[9], Figure 9는 기초설계한 림추진기와 Opt7의 버블 캐비테이션 영역(3.0 kPa 이하인 영역)을 NCR 조건에서 비교한 것이다. Figure 10은 NCR의 조건에서 기초설계한 림추진기와 최적화한 림추진기의 버블 캐비테이션 영역에 대한 핵압이 각각 –6.6 kPa과 –3.1 kPa임을 보이고 있다. 최적화된 림추진기는 광범위한 영역에서 받음각이 증가되었음에도 불구하고 Figure 9와 Figure 10에 보인 바와 같이 캐비테이션 정도는 오히려 감소하였음을 알 수 있다. 이 결과는 림추진기의 유동특성이 3차원적임을 의미한다. 즉, 림추진기 깃의 특정반경에서의 압력분포는 반경방향으로 인접한 깃 주변의 압력분포에 영향을 받을 뿐만 아니라, 반경방향의 속도성분을 무시할 수 없다. 받음각의 최적화를 통하여 캐비테이션을 감소시킬 수 있음을 보인 참고문헌을 찾을 수는 없었으나, 본 연구는 받음각의 최적화가 캐비테이션의 저감 측면에서 효과적임을 보이고 있다.
3.5 탈설계조건에 대한 수치해석결과
설계조건과 마찬가지로 탈설계조건에서의 림추진기의 성능 또한 매우 중요하다. 또한, A. J. Dubas [7]의 연구결과를 살펴보면 림추진기의 최적화는 높은 전진수에서 보다 높은 효율 상승을 기대할 수 있다. 그러므로 본 연구에서는 탈설계조건에 대한 성능분석을 추가적으로 수행하였다.
일반적으로 추진기의 성능곡선은 전진수(J)에 대하여 추력 계수(KT)와 토크 계수(KQ) 그리고 추진기 단독효율(ηPOW)로 나타낼 수 있다. 각 변수의 정의는 식 (1) ~ 식 (4) 와 같다.
| (1) |
| (2) |
| (3) |
| (4) |
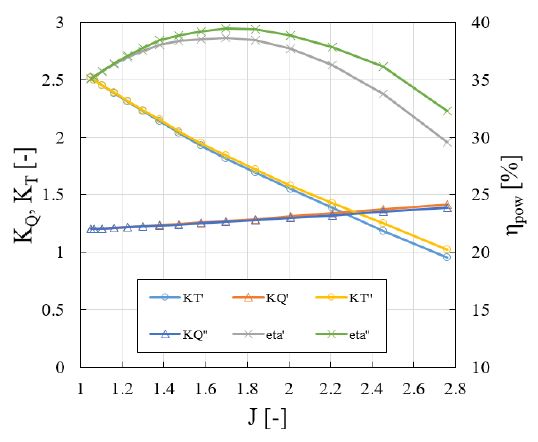
CFD를 이용한 Opt7의 성능분석 결과는 Figure 11과 같다. 전진수(J)에서 CFD를 통하여 조작 가능한 변수는 전진속도(Va: m/s)와 회전속도(n: rps)이다. 전진속도(Va)를 설계조건으로 일정하게 유지하고 회전속도를 설계회전속도의 0.4에서 1.05 (step: 0.05) 까지 CFD 해석을 수행한 결과는 Figure 11에 상첨자 `(single prime)로 표시하였고, 회전속도를 NCR 조건인 483 rpm으로 일정하게 유지하고 전진속도(Va)를 조작하여 얻은 CFD 결과는 상첨자 `` (double prime)로 표시하였다.
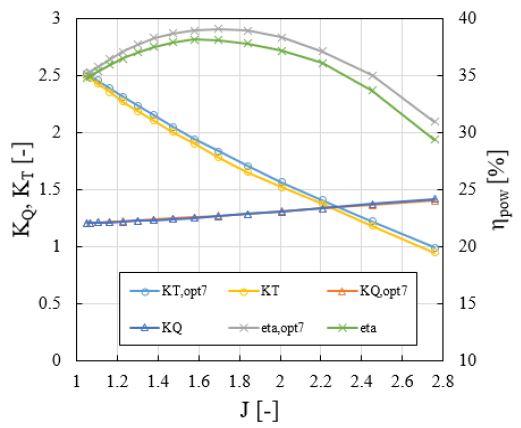
Figure 11에서 상첨자 `(single prime) 와 상첨자 `` (double prime)로 표현한 Opt7의 추력 계수, 토크 계수, 추진기 단독효율에 대한 각각의 성능지표를 평균하고, 기초설계한 림추진기의 각각의 성능지표와 비교하면 Figure 12와 같다. Figure 12는 탈설계조건에서 고려된 전진수 범위 내에서 Opt7의 림추진기 단독효율이 기초설계한 림추진기의 단독효율보다 항상 높으며, 최적화를 통하여 최대 약 1.6 %에서 최소 약 0.4 %의 효율 상승을 기대할 수 있다는 것을 보여준다. 최대효율 상승을 기대할 수 있는 전진수 범위는 A. J. Dubas [7]의 연구결과와 마찬가지로 전진수가 높은 범위이다.
그러나, 본 연구와 같이 받음각의 최적화만으로 기대할 수 있는 효율 상승의 정도는 상당히 제한적인 것으로 판단된다. 본 연구에서 CFD를 수행한 전진수 범위와 A. J. Dubas [7]가 고려한 전진수 범위가 서로 다르며 두 연구의 설계조건 및 림추진기 형상 또한 크게 다름을 고려할 지라도 본 연구에서 최적화를 통하여 얻는 효율 상승의 정도는 A. J. Dubas [7]가 림추진기의 최적화를 통하여 효율을 상승시킨 최대량(약 6%)과 비교하여 작은 수준이다. A. J. Dubas [7]는 피치비 뿐만 아니라 림추진기의 직경, 코드/직경비, 덕트 외경 등과 같은 총 13개 파라미터를 이용하여 림추진기를 최적화한 것에 주목하여 살펴본다면, 향후 림추진기에 대한 다양한 파라미터의 최적화에 대한 추가적인 연구가 필요할 것으로 판단된다. 이러한 추가적인 연구를 통하여 림추진기의 보다 높은 효율상승 및 캐비테이션의 저감 등을 실현할 수 있을 것으로 판단된다.
4. 결 론
본 연구는 기초설계한 림추진기에 대한 최적화에 대한 연구이다. 림추진기는 덕트의 유기속도와 림의 회전운동 등으로 인하여 고전적인 추진기와는 다른 유동특성을 가진다. 그러므로 림추진기가 가지는 고유한 유동특성을 반영하여 기초설계한 림추진기를 최적화할 필요가 있다.
본 연구에서는 CFD를 이용하여 림추진기의 받음각을 최적화하고 목표출력의 달성을 위하여 추진기의 출구각도를 조정하는 일종의 시행착오의 방법(Method of trial and error)을 제시하였다. 그 결과 본 연구에서 제시한 시행착오의 방법을 통하여 림추진기를 최적화할 경우 출력은 일정하게 유지하면서 효율의 상승 및 캐비테이션의 저감 효과를 기대할 수 있음을 알 수 있었다.
그러나 본 연구의 경우 받음각의 최적화를 통한 효율의 상승 정도는 그다지 크지 않은 수준이었다. 향후 림추진기에 대한 보다 다양한 형상 파라미터에 대한 최적화 연구를 진행할 예정이다.
Nomenclature
| Cθ : | swirl component of absolute velocity [m/s] |
| Cz : | axial component of absolute velocity [m/s] |
| F : | thrust force [N] |
| i : | attack angle [degree] |
| KQ : | torque coefficient [-] |
| KT : | thrust coefficient [-] |
| LE : | leading edge |
| MCR : | maximum continuous rating [kW] |
| N : | rpm |
| NCR : | normal continuous rating [kW] |
| n : | rps |
| PD : | delivery power [kW] |
| PE : | effective power [kW] |
| Q : | torque [kN·m] |
| r/R : | propeller radius ratio [-] |
| TE : | trailing edge |
| Va : | advance speed [m/s] |
Greeks
| α1,CFD : | inflow angle based on the CFD result |
| β1 : | blade inlet angle |
| β2 : | blade outlet angle |
| ηPOW : | propeller efficiency at open water [%] |
| ρ : | density [kg/m3] |
| σs : | slip factor [-] |
| ω : | angular velocity [rad/s] |
Acknowledgments
본 연구는 산업통상자원부와 한국산업기술진흥원의 “소형선박용 150kW급 림 구동 전기추진시스템 개발” 사업으로 수행된 결과입니다(과제번호: P0002106).
Author Contributions
Investigation, D. Y. Kim and Y. T. Kim; Methodology, D. Y. Kim; Investigation, D. Y. Kim; Writing-Original Draft, D. Y. Kim; Writing-Review & Editing, Y. T. Kim and D. Y. Kim; Supervision, Y. T. Kim; Funding Acquisition, Y. T. Kim;
References
-
D. Y. Kim and Y. T. Kim, “Fundamental design of a 75-kW-rim-driven propeller,” Journal of the Korean Society of Marine Engineering, vol. 43, no. 1, pp. 31-39, 2019 (in Korean).
[https://doi.org/10.5916/jkosme.2019.43.1.31]

-
X. Yan, X. Liang, W. Ouyang, Z. Liu, B. Liu, and J. Lan, “A review of progress and applications of ship shaft-less rim-driven thrusters” Ocean Engineering, vol. 144, pp. 142–156, 2017.
[https://doi.org/10.1016/j.oceaneng.2017.08.045]

-
S. Zhang, X. Zhu, and Z. L. Zhou, “Hydrodynamic Performance Analysis of Hubless Rim-Driven Propulsors,” Applied Mechanic and Materials, vol. 256, pp. 2565–2568, 2013.
[https://doi.org/10.4028/www.scientific.net/AMM.256-259.2565]

-
B. W. Song, Y. J. Wang, and W. L. Tian, “Open water performance comparison between hub-type and hubless rim driven thrusters based on CFD method,” Journal of Ocean Engineering, vol. 103, pp. 55–63, 2015.
[https://doi.org/10.1016/j.oceaneng.2015.04.074]

-
A. Santoso, I. S. Arief, and A. T. Kurniawan, “Performance analysis rim driven propeller as a propulsor using open water test,” International Journal of Marine Engineering Innovation and Research, vol. 2, no. 1, pp.70-76, 2017.
[https://doi.org/10.12962/j25481479.v2i1.2470]

-
M. F. Hsieh, J. H. Chen, Y. H. Yeh, C. L. Lee, P. H. Chen, Y. C. Hsu, and Y. H. Chen, “Integrated design and realization of a hubless rim-driven thruster,” The 33rd Annual conference of the IEEE Industrial Electronics Society, pp. 3033–3038, 2007.
[https://doi.org/10.1109/IECON.2007.4460298]

- A. J. Dubas, Robust Automated Computational Fluid Dynamics Analysis and Design Optimisation of Rim Driven Thrusters, Ph.D. Dissertation, Department of Engineering Sciences, University of Southampton, UK, 2014.
-
Q. M. Cao, F. W. Hong, D. H. Tang, F. L. Hu, and L. Z. Lu, “Prediction of loading distribution and hydrodynamic measurements for propeller blades in a rim driven thruster,” Journal of Hydrodynamics, vol. 24, no. 1, pp. 50-57, 2012.
[https://doi.org/10.1016/S1001-6058(11)60218-7]

-
A. F. Molland, S. R. Turnock, and D. A. Hudson, Ship Resistance and Propulsion, Cambridge University Press, 2017.
[https://doi.org/10.1017/9781316494196]