함정 추진체계 동적 시뮬레이션을 위한 가변추진기 수학 모델 개발
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 함정 설계 단계에서 시뮬레이션을 통해 함정의 성능을 예측할 수 있는 함정 추진체계 동적 시뮬레이션 소프트웨어의 일부인 가변추진기 수학 모델의 개발을 목표로 하고 있다. 본 연구의 개발 모델은 현재까지 개발되어진 가변추진기 수학모델과 달리 캐비테이션 판정 내용을 포함하고 있다. 캐비테이션 판정은 Burrill's cavitation diagram를 활용하였으며, 본 연구의 개발 모델은 모든 운용 상황에서의 캐비테이션 발생을 예측할 수 있는 기능을 담고 있다. 본 연구에서는 가변추진기의 동적 특성을 고려하기 위해 동적 프로펠러 단독시험을 진행하였으나 정적시험과 동적시험에 큰 차이가 없는 것을 확인하였으며 이에 따라 가변추진기의 동적 특성을 무시해도 된다고 판단하였다. 본 연구에서 개발한 가변추진기 수학모델의 성능 검증을 위해 계산 처리 시간 검증 시험, 외부 변수 계산 기능, 캐비테이션 판정 시험을 진행하였다. 그 중 핵심이 되는 외부 변수 계산 기능 시험은 시뮬레이션의 신뢰성과 관련된 시험으로써 검증용 데이터와의 차이가 5% 미만인 경우를 합격 기준으로 설정하였다. 각 운용 상황에서 가변추진기의 핵심 특성인 추력, 토크를 비교하였으며 최대 오차율이 약 3%로 모든 상황에서 합격 기준을 만족하는 것을 확인하였다.
Abstract
This paper presents the development of a numerical model of a controllable pitch propeller for the simulation of naval ship propulsion system dynamics. Unlike other previous models, this numerical model can determine the occurrence of cavitation using Burrill's cavitation diagram, especially the curve for warship propellers with special sections. Furthermore, a dynamic POW test was conducted to analyze how the characteristics of the controllable pitch propeller (especially thrust and torque) were affected when the advanced ratio changed considerably. However, the results of the test were not significantly different when compared with the static POW test; therefore, the dynamic characteristics of the controllable pitch propeller were ignored. To verify the performance of the numerical model, three verification tests were conducted, namely, computational processing time, external variable calculation function, and cavitation calculation function. Among these tests, the acceptance criteria of the external variable calculation function test, which is related to the reliability of the simulation results, were set to pass when the differences between the simulation results and verification data were < 5%. Thrust and torque, which are significant characteristics of a controllable pitch propeller, were compared under all operational conditions. Finally, the maximum error rate was confirmed to be 3%.
Keywords:
Naval ship, Controllable pitch propeller, Dynamic simulation, Cavitation, POW test키워드:
함정, 가변추진기, 동적 시뮬레이션, 캐비테이션, 프로펠러 단독시험1. 서 론
함정 설계 및 건조단계는 선행연구, 탐색개발, 체계개발 단계로 구분되며, 일반적으로 추진체계 설계는 탐색개발 단계에서 수행되며 추진체계 형태 및 배치, 탑재장비 기종결정 등이 이루어진다. 그러나 함정 탐색개발 단계에서는 추력대비 함속변화, 과기동(긴급기동/긴급정지/급선회)시의 함속변화에 대한 검증이 불가능한 실정이다. 이러한 성능은 시운전단계에서 확인이 가능하나, 시운전 단계에서 추진체계 설계오류 개선은 많은 비용과 기간을 동반하며 함정 적기 인수 및 전력화 지연에 영향을 미칠 수 있다. 위와 같은 문제를 해결하기 위해서는 함정 설계 단계에서 미리 함정추진체계의 통합성능을 예측할 수 있어야 하며, 이에 따라 함정추진체계 동적 시뮬레이션 소프트웨어의 필요성이 대두되고 있다.
함정추진체계 동적 시뮬레이션은 총 5개의 수학 모델로 구성되며 본 연구는 가스터빈, 추진전동기, 축계, 가변추진기, 함정 모델 중 추진기의 수학 모델에 관한 연구이다. 대상이 된 추진기는 가변추진기(CPP)로 함정의 운용 상황에 따라 다양하게 바뀌므로 신뢰성과 범용성을 확보할 수 있도록 가변추진기 수학 모델을 제시 하였다.
2. 가변 추진기 수학 모델 개발 동향 및 특징
조종성능 추정 모델인 MMG(Mathematical Maneuvering Group)에서는 선박의 운동방정식을 풀기 위해 추력을 주요한 변수로 보고 있으며, 이 추력을 3차 다항식으로 구성하고 있다. 자세하게 프로펠러 단독 성능 모형시험(POW)을 통해서 구한 전진비에 따른 추력을 수식화 하였으며, 선박 운항 시 유입 유속에 대한 회전수의 비인 전진비를 구하여 동일 전진비 상황에서 동일한 추력을 발생시키는 모델을 사용하고 있다. 기존 연구 개발 사례는 Genoa 대학과 Fincantiery사의 함정추진기 동적 모델 개발 연구[1]가 있다. 개발한 동적 모델에서는 함정의 시운전 결과를 바탕으로 평균 유효 반류를 찾는 작업을 수행하였으며, 이를 데이터화 하여 프로펠러 단독 특성 곡선을 이용하여 운항 시 추력과 토크 값을 계산 하였다. 프로펠러 단면에 유입되는 받음각(angle of attack)은 프로펠러의 추력, 토크, 효율 특성을 좌우하기 때문에 전진비와 프로펠러 피치 변경이 추력 및 토크를 계산하는데 있어 중요한 요소가 된다. 따라서 가변추진기 수학모델에서 프로펠러의 피치, 유입 유속, 회전수가 중요한 변수가 된다. 본 모델에서는 유입유속의 속도, 프로펠러의 회전수, 프로펠러의 피치를 변수화 하여 회귀 분석을 수행하여 수식화 하고자 한다. 또한 프로펠러의 단독특성을 수식화 하고자 한다.
가변추진기 계산에 있어 중요한 요소는 전진비에 따른 추력과 토크 특성이다. 전진비를 알기 위해서는 선박의 속도, 반류, 프로펠러 회전수, 프로펠러 직경에 대한 정보가 필요하다. 선박의 속도, 프로펠러 회전수, 프로펠러 직경은 초기 설계단계에서 결정된 값이므로 반류 값에 대한 추정 또는 계산이 필요하다. 프로펠러에 유입되는 반류 측정은 거의 불가능하기 때문에 모형시험에서는 프로펠러의 추력과 선박의 저항을 이용하여 반류를 역추정 하는 방법을 주로 쓰게 된다[2]. 간단하게 선박의 저항과 일치하는 추력값을 찾아 그때 전진비를 추정하면 반류가 고려된 프로펠러 유입속도를 알 수 있다. 이는 프로펠러를 일종의 유속계로 사용하는 것이다. 본 가변추진기 모델을 개발하는데 있어 프로펠러에 유입되는 평균 유속은 굉장히 중요한 정보가 되며 반류 계산은 3.4절에서 논의하고 있다.
Genoa 대학교에서는 rudder angle, ship speed, drift angle 정보를 이용하여 반류를 추정하는 모델을 적용하였다[1]. 국내 조선소에서는 프로펠러 설계 및 해석 관점에서 추진기에 대한 연구를 진행하고 있으며, 최대 관심사는 주어진 엔진과 선형에 따른 계약 선속의 달성여부이다. 일반적으로는 위와 같은 프로펠러의 설계 검증을 위해서 CFD (전산유체역학)해석과 모형시험을 수행하고 있는 실정이다.
조종성능 평가를 위해서는 추진기 수학모델을 주로 사용하고 있다. MMG 조종성능 시뮬레이션 시 전진비에 따른 추력을 근사하여 사용하고 있다. 프로펠러의 전진비에 따른 추력요소가 모형시험을 통해 확보된 경우 그 값을 사용하고, 그 외에 전진비에 따른 경험식을 사용하고 있다. 수학모델 개발 시 프로펠러 특성 정보 획득 방법 및 그에 따른 특성은 아래 Table 1 과 같다. 본 연구에서는 추진기 제작사에서 제공해주는 프로펠러 특성 값을 기준으로 수학모델을 개발하고 있다.
3. 가변 추진기 수학 모델의 구성 및 검토
3.1 피치제어
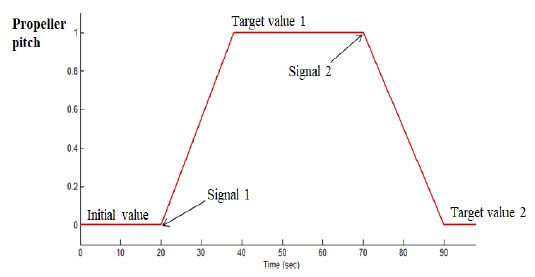
피치비는 프로펠러가 1회전 할 때 선박의 길이방향으로 전진하는 거리와 직경의 비를 나타내며 가변추진기의 경우 운용환경에 따라 피치비가 변화하며 이에 따라 추력과 토크가 달라진다. 프로펠러의 피치는 유압 제어에 의해 운전자가 원하는 피치비에 도달하기 까지 다소 시간이 소요된다. 유압 장비와 프로펠러 부하에 따른 지연 효과 또한 발생할 수 있으나, 본 연구에서는 피치의 변화 속도가 느리기 때문에 선형적으로 변화하도록 구성하였다. Figure 1과 같이 목적 피치비가 명령으로 들어오게 되면 가변추진기 사양에 명시된 피치 변화 속도가 고려되어 피치비가 선형적으로 증감하여 목적 피치비에 도달하도록 구성하였으며, 피치비가 제한된 범위를 초과하는 경우 최대 피치비로 수렴하도록 구성하였다.
3.2 캐비테이션 판정
캐비테이션은 프로펠러가 빠른 회전수로 회전함에 따라 동압이 상승하고 베르누이 법칙에 의해 정압이 감소하여 프로펠러 주변의 물이 상온에서 기화하는(끓는) 현상을 말한다. 함정 프로펠러의 경우 캐비테이션 문제에 민감하기 때문에 각 운용상태에서의 캐비테이션 발생가능성을 예측 하는 것은 중요한 성능이 될 수 있다.
캐비테이션 발생을 예측하기 위해서는 먼저 해당 프로펠러의 캐비테이션 시험을 진행하여 특정 캐비테이션 수(αn) 에서의 발생정도를 정의해야 하지만 본 연구의 목적은 설계단계에서의 성능 예측을 목표로 하기 때문에 시험이 불가능한 실정이다. 이에 따라 본 연구에서는 Burrill's cavitation chart [3]를 이용하여 캐비테이션 발생 판정을 구성하였다.
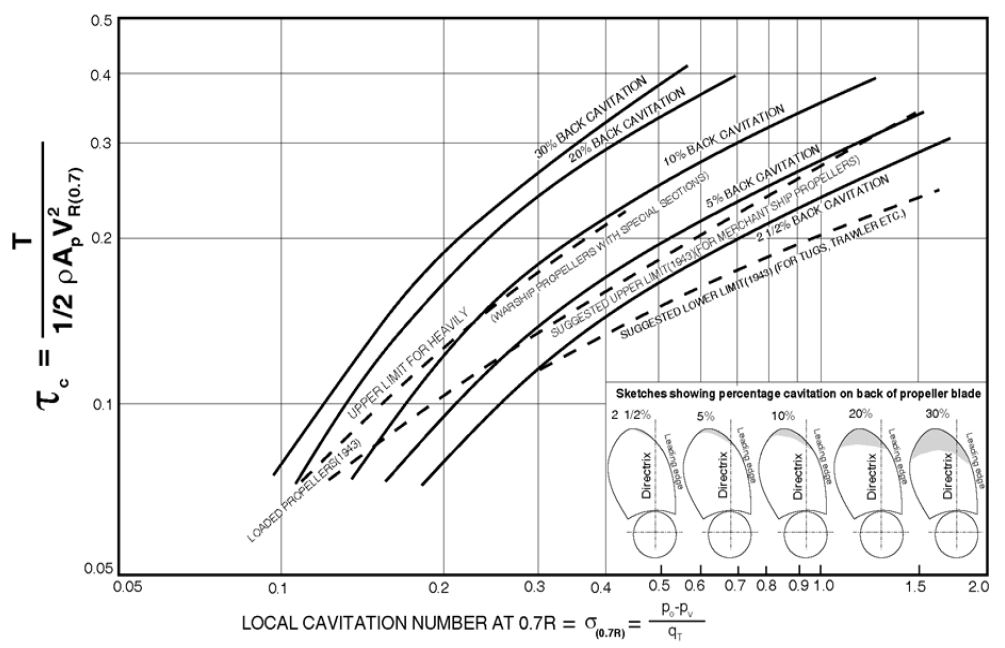
Burrill's cavitation chart는 Figure 2와 같이 x축은 캐비테이션 수, y축은 추진하중계수로 정의되어있으며 여러 개의 곡선을 이용하여 여러 선종의 캐비테이션 발생 기준을 정의하였다. 본 연구에서는 Figure 2에 점선으로 나타내어진 (Warship propellers with special sections) 곡선을 기준으로 캐비테이션 발생을 판단하였다. 하지만 Burrill's cavitation chart가 약 1960년대 작성되어진 점과 본 연구에 활용한 곡선이 약 10% 이상의 캐비테이션 발생을 나타낸다는 점을 미루어 볼 때 곡선 선택에 있어 다소 검토가 필요하다고 판단되어진다.
3.3 피치 변화에 따른 비선형성 분석
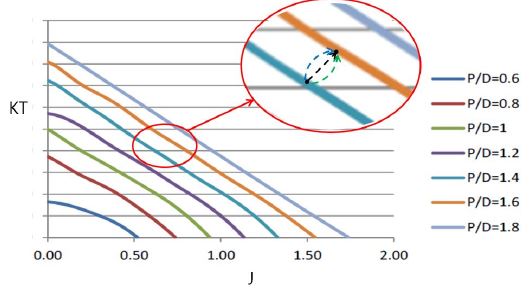
Figure 3은 다양한 피치비(P/D: 0.6 ~ 1.8)에 대하여 추력계수(KT)를 나타내고 있다. 전진비와 피치비에 의해 결정되어지는 추력계수 및 토크계수는 선형보간법을 통해 구해진다. 하지만 실제로 유체 내에서 작동하는 가변 추진기는 전진비 또는 피치비의 변화속도가 빠를 경우 Figure 3의 그림 확대된 부분의 검은색 점선과 같이 선형적으로 변화하지 않고 파란색, 녹색 점선과 같이 비선형적인 변화가 있을 수 있다. 이는 피치비 변화 속도에 따라, 혹은 운용 시나리오(Slam start, Crash stop 등)에 따른 전진비의 변화속도에 따라 추력계수와 토크계수의 보간을 다르게 적용해야한다는 것을 뜻한다. 시간에 따른 전진비의 급격한 변화에 대해서 프로펠러 추력과 토크의 비선형적 변화를 확인하기 위해 본 연구에서는 유사 모형프로펠러(CPP, 5-blades, high skewed)의 POW시험을 진행하였다.
모형시험은 부산대학교 선박예인수조에서 수행하였다. 예인수조 시설의 제원은 길이 100m, 너비 8m, 깊이 3.5m이며, 예인전차 최고 운행 속도는 4m/s이다. 모형 프로펠러의 제원은 Table 2과 같다. 모형 프로펠러의 특성 상 피치 변경이 불가능하기 때문에 전진비 변화만 고려하였으며, 동적 시험을 하기 앞서 정적 시험을 진행하여 기준을 설정하였다. 정적 시험은 일반적인 POW시험과 동일하게 회전수를 고정한 상태에서 선속만을 변경하여 전진비의 변화를 주었다.
본 연구의 대상 함정이 Slam start시 최대 선속 변화율은 초당 0.4노트 이다. 본 연구에서는 보다 극한 상황을 가정하여 초당 0.6노트의 선속변화를 설정하였다. 이를 전진비로 계산하면 초당 약 0.1정도이다. 본 시험에서는 시간에 따라 전진비가 변화하는 여러 경우를 계획하였으며, 상세 조건은 Table 3에 나타내었다. 아래 Dynamic 4의 경우가 5초 동안 초당 약 0.1의 전진비로 변화 시킨 경우 이고 나머지 조건은 그 보다 전진비 변화율이 작은 경우 이다.
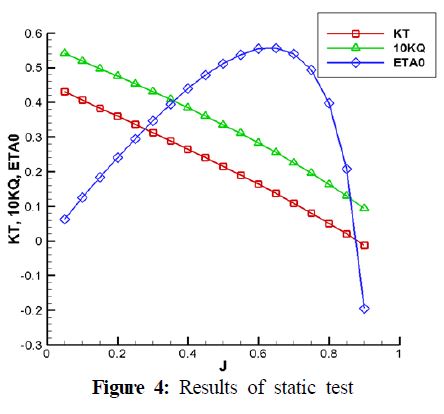
정적시험 결과는 Figure 4에 나타내었다. Figure 4는 일반적인 Propeller Open Water 시험 결과와 같으며 전진비(J)에 따른 프로펠러 추력계수(KT)과 토크계수(KQ) 그리고 효율(ETAO)특성을 나타내고 있다. 정적시험은 프로펠러 회전수와 선속을 고정하여 일정시간 측정한 데이터를 평균한 것이다.
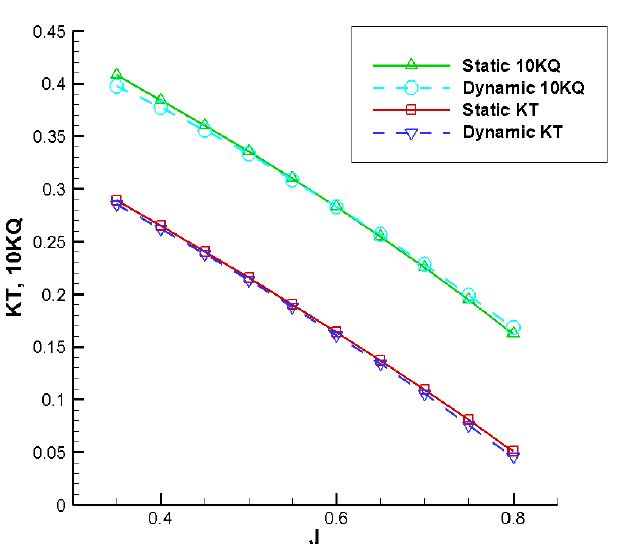
동적시험은 선속을 고정하고 프로펠러 회전수를 계측 시간 동안 Table 3와 같이 변경하여 데이터를 측정하였다. 이 경우 회전수의 변경으로 인한 서보 모터 노이즈가 포함될 소지가 있어 Low Pass Filter기법을 이용하여 데이터 노이즈를 줄여주었으며[4], Figure 5 에 정적시험과 비교하여 나타내었다. Figure 5 는 전진비(J)에 따른 추력계수(KT)와 토크계수(KQ)를 비교한 그림이다. 실선으로 표시된 그래프가 정적시험결과(static)이며, 점선으로 표시된 그래프가 동적시험결과(dynamic)이다.
정적시험결과와 동적시험결과의 차이는 전진비 별로 약간의 차이를 보였지만 상대적으로 노이즈가 적은, 신뢰성이 높은 구간에서의 결과 차이는 2% 미만인 것을 확인하였다. 이에 따라 본 연구에서는 급격한 전진비 변화에 따른 비선형성을 고려하지 않는 것으로 결정하였다.
3.4 반류 계산
프로펠러로 유입되는 반류를 계측하는 일은 거의 불가능하기 때문에 일반적으로는 자항시험에서의 추력과 프로펠러 단독상태의 추력을 이용한다[5]. 동일한 추력을 내는 서로 다른 전진비의 차이를 이용하여 반류를 역추정 할 수 있다. 본 연구에서는 이와 유사한 방법을 이용하였으며, 프로펠러 제작사에서 제공하는 Combinator law와 POW data에서의 토크를 활용하여 반류를 계산하였다.
프로펠러 제작사로부터 제공받은 Combinator law에는 각 선속에서의 프로펠러의 전달동력이 명시되어 있는데, 이를 이용하여 아래와 같은 수식을 통해 토크 및 토크계수를 계산할 수 있다.
| (1) |
| (2) |
| (3) |
- PD : 전달 동력
- Qb : 프로펠러 토크(behind)
- KQb : 프로펠러 토크계수(behind)
- n : 프로펠러 회전수
- D : 프로펠러 직경
여기서 아래첨자 b는 behind condition의 줄임말로 선체 뒤에서의 프로펠러 구동 조건을 뜻한다. Combinator law의 각 전진비와 피치비에 해당하는 토크계수와 POW data의 동일 피치에서 동일 토크계수를 갖는 서로 다른 두 전진비를 아래 식을 이용하여 반류를 계산할 수 있다.
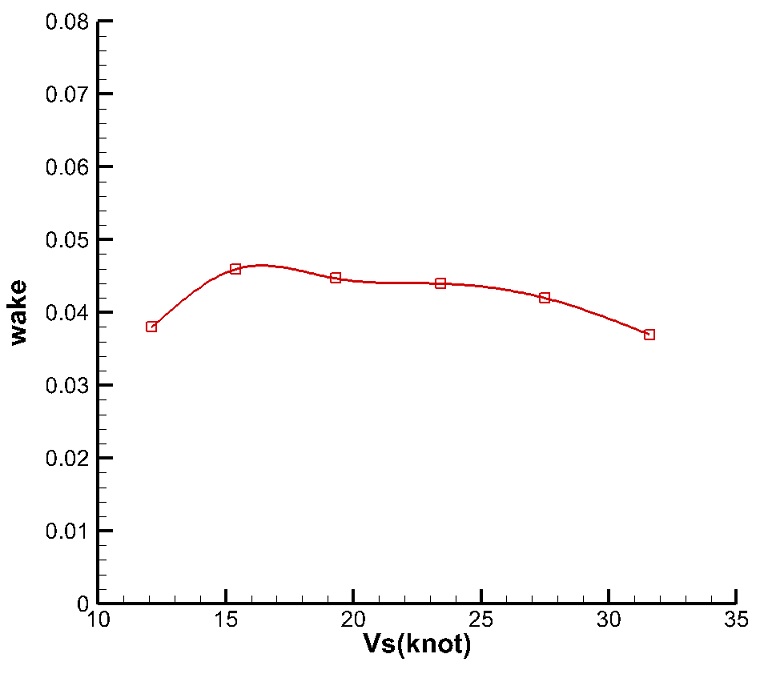
반류 계산 결과는 Figure 6에 나타내었으며, 각 선속에서 대략 0.035~0.045의 값을 갖는 것을 확인할 수 있다. 이에 따라, 본 연구에서는 설계속도 반류값인 0.04로 설정하여 진행하였다. 반류값 설정에 따른 전진비 오차는 0.5% 이내 이다.
| (4) |
| (5) |
| (6) |
4. 가변추진기 수학 모델 검증
가변추진기 수학 모델의 검증을 위해 본 연구에서는 계산 처리 시간 시험, 외부 변수 계산 기능 시험, 캐비테이션 판단 시험을 수행하였다.
4.1 계산 처리 시간 시험
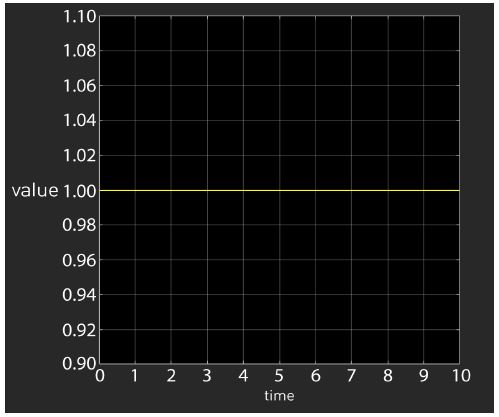
계산 처리 시간 시험은 시뮬레이션 수행 시 가변추진기 수학모델을 1회 계산하는데 소요되는 시간을 확인하는 시험이다. 계산 처리 시간은 계산 출력 시간인 1초를 초과하지 않는 것을 합격 기준으로 설정하였다. 그 기준은 시뮬레이션상 1초이내 계산이 처리되어야 실시간 시뮬레이션이 가능하기 때문이다. 시험 수행 결과, Figure 7과 같이 가변추진기 수학모델을 10초 시뮬레이션 하는데 계산 시간이 약 1.25초가 소요되는 것을 확인하였다. 따라서 1초 계산 시간은 0.125초로 기준을 만족하였다. 시뮬레이션에 사용한 컴퓨터의 CPU는 I7-3770으로 클럭속도는3.40GHz 이며, Ram 용량은 16Gb이다. 시뮬레이션코드 작성 및 실행 프로그램은 Matlab 2018의 Simulink이다.
4.2 외부 변수 계산 기능 시험
외부 변수 계산 기능 시험은 가변추진기 모델의 입력값으로 들어오는 외부 변수들의 변화에 따라 시뮬레이션의 결과값이 적절히 변하는지를 확인하기 위한 시험이다. 외부 변수 계산 기능 시험은 Combinator law와 모형시험 결과를 검증용 데이터로 활용하였으며 내용은 아래와 같다.
가변추진기 모델은 Combinator law상의 회전수, 피치비, 선속을 입력값으로 하여 가변추진기 시뮬레이터를 구동한다. 시뮬레이션 결과값인 토크와 Combinator law상의 전달동력을 이용하여 계산한 토크를 비교함으로써 기능에 대한 검증을 실시한다.
- ① Combinator Law 특정 lever 데이터 확보
- ② Pitch비와 선속 자료 입력
- ③ 회전속도정보 입력
- ④ 가변추진기모델 프로그램 실행
- ⑤ 가변추진기 모델 토크 및 전달 동력과 Combinator Law결과 비교
- ⑥ 비교 그래프 작성
- ⑦ 결과 검토 및 오차 확인
가변추진기 모델은 Combinator law 상의 회전수, 피치비, 선속을 입력 값으로 하여 가변추진기 시뮬레이터를 구동한다. 시뮬레이션 결과 값인 추력과 모형시험 결과값의 단독효율, 상대회전효율, 전달동력, 회전수, 선속들을 이용하여 계산한 추력을 동일 선속에서 비교함으로써 기능에 대한 검증을 실시한다.
- ① 모형시험결과의 특정 속도에서 데이터 확보
- ② Pitch비와 선속 자료 입력
- ③ 회전속도정보 입력
- ④ 가변추진기모델 프로그램 실행
- ⑤ 가변추진기 모델 추력 모형시험 결과 비교
- ⑥ 비교 그래프 작성
- ⑦ 결과 검토 및 오차 확인
외부 변수 계산 기능 시험의 합격 기준은 검증용 데이터와 실제 시뮬레이션 결과 값의 오차율이 5%를 넘지 않는 것으로 설정하였으며, 이는 일반적으로 신뢰성을 가진 CFD해석과 모형시험의 차이가 약 2~8% 차이가 나는 것을 배경으로 하였다[6]-[8].
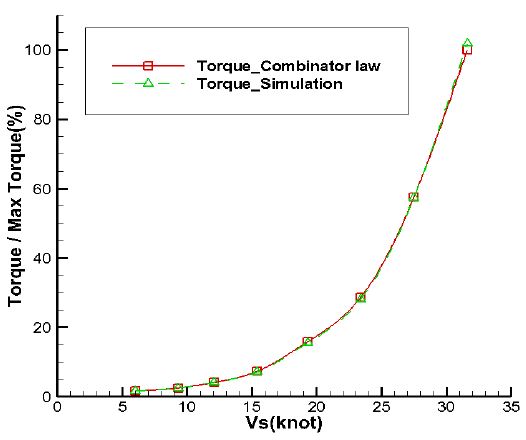
모델 검증 기준이 되는 데이터는 Combinator law와 모형시험 결과를 이용하였다. Combinator law에서는 선속, 피치비, 회전수에 따른 전달동력이 명시되어있는데, 이를 통해 토크를 계산할 수 있기 때문에 전달동력 및 토크를 평가할 수 있으며, 모형시험에서는 여러 자항계수를 통해 추력을 계산할 수 있기 때문에 추력을 평가할 수 있다.
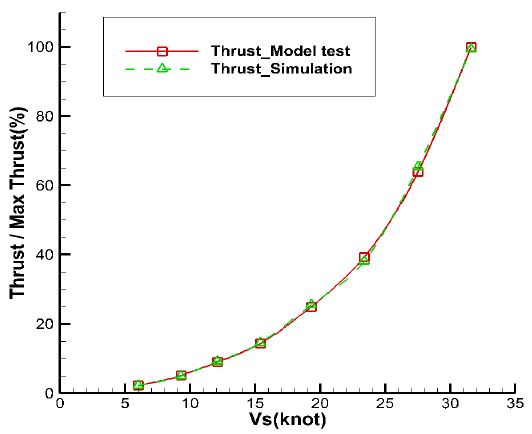
모형시험을 통한 추력계산결과와 시뮬레이션을 통한 선속별 추력 계산결과는 Figure 9와 같이 상당한 일치를 보여 주고 있다. Combinator law의 선속에 따른 토크 결과와 본 시뮬레이션 결과도 Figure 10과 같이 신뢰성 높은 결과를 보여 주고 있다. 전체적으로 가장 큰 오차가 약 3%로 합격기준에 적합한 것을 확인하였다.
4.3 캐비테이션 판정 시험
Figure 2에 점선으로 나타내어진 warship propeller 기준으로 설계 피치 상태에서 캐비테이션이 발생하는 속도를 검토 해 보았다. 프로그램의 판단기준은 캐비테이션 수 와 추진하중계수를 검토하여 그래프를 벗어나서 캐비테이션이 발생하면 1로 나타내고 그 외 경우는 0으로 표현되도록 하였다.
기준 피치비 1.0, 회전수 100rpm 조건에서 속도에 따른 캐비테이션 발생여부 검토 결과 아래 Figure 8과 같이 19.8knot일 때 1로 나타내었고, 이는 시뮬레이션 조건에서 10% 캐비테이션이 발생 한다는 것이다.
이는 실선기준으로 다소 높은 속도에서 캐비테이션이 발생하는 것으로 판단된다. 따라서 캐비테이션을 보다 정확하게 판단하기 위해서 보다 엄격한 기준과 더불어 시험 자료가 필요 할 것으로 판단된다.
5. 결 론
가변추진기 시험프로그램 개발을 위해서 국내외 가변 추진기 수학모델 개발 사례를 조사하였으며, 가변추진기의 수학모델을 구성하기 위한 방법으로는 2절과 같이 데이터 베이스 활용, 모형시험 수행, 해석적 수행, 추진기 제작사 제공 특성치 정보가 있는 것을 확인하였다. 위의 다양한 방법 중 본 연구에서는 시간적 제약이 작고 신뢰도 측면에서 가장 활용도가 높은 추진기 설계사 제공 특성치 활용 방법을 선택하여 연구를 진행하였다. 본 연구에서 개발한 가변추진기 수학모델은 가변추진기의 특성치인 추력 및 토크 뿐만 아니라 피치비 조절 기능과 캐비테이션 판정 기능을 추가적으로 담고 있다.
본 연구에서는 가변추진기가 급격하게 구동조건을 변경하는 경우에 추력 및 토크에는 어떠한 영향을 미치는지를 알아보기 위해 동적 POW 시험을 수행하였다. 동적 POW 시험 결과는 정적 POW 시험 결과와 큰 차이가 없는 것을 확인하였으며, 본 연구에서는 이러한 동적 특성을 무시할 수 있다고 판단하였다. 따라서 피치비 변화 전진비 변화에 따른 선형보간에 대한 신뢰성을 확보 하였다.
본 연구에서는 가변추진기 수학모델을 검증하기 위한 시험을 진행하였다. 시뮬레이션 상 시간 1초를 계산하기 위한 실제시간이 0.125초로 시뮬레이션을 수행하기에 적합한 것으로 확인되었다. 선속에 따른 추력과 토크 특성을 확인해본 결과 오차가 3% 이내로 시뮬레이션을 수행하기에 신뢰성이 높은 것으로 확인 되었다. 캐비테이션 판정을 수행해본 결과 실제보다 높은 선속에서 캐비테이션이 발생하는 것으로 판단되어 보다 엄격한 기준 또는 시험을 바탕으로 한 연구가 추가적으로 수행되어야 할 것으로 판단된다.
본 연구 결과가 피치비와 전진비에 따라 추진특성이 변하는 가변추진기와 관련된 연구를 수행하기 위한 자료로 활용가능성이 있다고 판단된다.
Acknowledgments
본 연구는 핵심SW(응용연구) “함정 추진체계 동적 시뮬레이션SW” 연구개발 사업과 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구이다(NRF-019R1F1A1058080).
Author Contributions
Conceptualization, K. W. Lee and M. C. Kim; Methodology, K. W. Lee; Software, K. Y. Yu; Validation, K. W. Lee and M. C. Kim; Formal Analysis, K. W. Lee; Investigation, S. C. Park; Resources, D. J. Kim; Data Curation, J. S. Kim; Writing—Original Draft Preparation, K. W. Lee; Writing—Review & Editing, M. C. Kim; Visualization, K. Y. Yu; Supervision, M. C. Kim; Project Administration, M. C. Kim; Funding Acquisition, M. C. Kim;
References
- M. Viviani and M. Altosole, “Marine propulsion system dynamics during ship manoeuvers,” Proceedings of 6th International Conference on High-Performance Marine Vehicles, pp. 81-93, 2008.
-
A. Coraddu, G. Dubbioso, S. Mauro, and M. Viviani, “Analysis of twin screw ships' asymmetric propeller behaviour by means of free running model tests,” Ocean Engineering, vol. 68, pp. 47-64, 2013.
[https://doi.org/10.1016/j.oceaneng.2013.04.013]

-
L. Burrill and A. Emerson, “Propeller cavitation: Further tests on 16 in. propeller models in the king's college cavitation tunnel,” International Shipbuilding Progress, vol. 10, no. 104, pp. 119-131, 1963.
[https://doi.org/10.3233/ISP-1963-1010402]

-
S. Tim, “A noise reduction method for signals from nonlinear systems,” Physica D: Nonlinear Phenomena, vol. 58, no. 1-4, pp. 193-201, 1992.
[https://doi.org/10.1016/0167-2789(92)90108-Y]

- C. S. Lee, J. C. Seo, B. S. Hyun, S. B. Seo, and M. C. Kim, Marine Propulsion and Design of Propellers, 2nd ed., Seoul, Korea: MUNUNDANG, 2012 (in Korean).
-
I. R. Park, “Numerical analysis of flow around propeller rotating beneath free surface,” Journal of Ocean Engineering and Technology, vol. 29, no. 6, pp. 427-435, 2015 (in Korean).
[https://doi.org/10.5574/KSOE.2015.29.6.427]

-
M. G. Kim, H. T. Ahn, J. T. Lee, and H. G. Lee, “Fully unstructed mesh based computation of viscous flow around marine propellers,” Journal of the Society of Naval Architects of Korea, vol. 51, no. 2, pp. 162-170, 2014 (in Korean).
[https://doi.org/10.3744/SNAK.2014.51.2.162]

-
T. H. Joung, S. J. Jeong, and S. K. Lee, “CFD simulations and experimental tests for three different ducted propellers,” Journal of Ocean Engineering and Technology, vol. 28, no. 3, pp. 199-208, 2014 (in Korean).
[https://doi.org/10.5574/KSOE.2014.28.3.199]