음향-구조 연성해석기법을 활용한 모형벌브수차 공진회피설계 검토
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
벌브수차를 비롯해 수중에서 운전되는 수차들은 구조물과 접하는 유체의 부가질량효과로 인해 고유진동수에 변화가 생긴다. 공진회피 설계를 위해서는 수차 실제 운용조건에서의 고유진동수를 파악해야 하며, 연성해석기법의 하나인 음향-구조 연성해석을 통해 이러한 사례를 분석할 수 있다. 본 연구에서는 실물수차 설계에 앞서 축소모형수차의 수중 고유진동수를 전산해석을 통해 구하고 이를 수력학적, 기계적, 전자기적 가진원들의 주파수와 비교하여 수차의 공진회피설계 여부를 확인했다. 해석결과 1~6차 수중고유진동수는 253.46~473.67Hz 범위에 분포했고, 이는 운전주파수, 깃통과주파수를 비롯한 다양한 수력학적 가진 주파수 및 전자기적 가진주파수와 최소 100% 이상 분리되어 이들 가진원에 대한 공진은 발생하지 않을 것으로 예상된다. 또한 동일한 해석기법과 분석절차는 향후 벌브형 수차를 비롯한 다양한 수차 설계에 적용할 수 있을 것이다.
Abstract
Hydro turbines as well as bulb turbine, which are operated in water, have different natural frequencies due to added mass effect of immersed structure in fluid compared with case of dried condition. Thus actual operational condition of turbine must be considered for resonance avoidance design and vibro-acoustic FSI can be a verifying solution of this analysis. In this study, natural frequencies of scale model turbine was attained using computational analysis then compared with frequencies of hydraulic, mechanical and electro-magnetical vibration sources in advance of real scale turbine design. As the result of FSI analysis, 1~6th natural frequencies of immersed condition were found within 253.46~473.67Hz. These frequencies have more than 100% separation with those hydraulic excitations as well as operation, blade passing, RSI, VIV, Karman vortex and electro-magnetic excitations, thus no probability of resonance will be expected in these excitations. This FE analysis method and verifying process can be applied to various hydro turbine as well as bulb turbine.
Keywords:
Bulb turbine, Natural frequency of immersed condition, Excitation source, Resonance avoidance design, Vibro-acoustic FSI키워드:
벌브 터빈, 수중 고유진동수, 가진원, 공진회피설계, 음향-구조 연성해석1. 서 론
에너지 자원이 절대적으로 부족하여 에너지의 국외의존도가 97% 이상인 우리나라는 국내 부존에너지를 최대한 활용해야 할 필요가 있다. 또한 지구 온난화에 대처하는 범세계적 규제에 대응하기 위해서도 청정에너지의 적극적 개발이 요구된다. 수력발전은 다른 신재생에너지원에 비해 에너지밀도가 매우 높아 개발가치가 큰 부존자원이다. 이들 가운데 벌브수차는 중-저낙차 환경에서 운용될 수 있어 국내 환경에 적합한 방식으로 평가된다.
회전기계인 수차는 회전에 의해 다양한 주기의 수력학적, 기계적, 전자기적 가진이 발생한다[1]. 수차의 수력학적 진동에는 VIV(Vortex Induced Vibration)라고도 불리는 드래프트 튜브부 와류에 의한 진동과 RSI(Rotor Stator Interaction)로 불리는 러너 입구부 압력맥동에 의한 진동, 러너 출구부 칼만 와류(Karman Vortex)에 의한 진동, 캐비테이션 진동 등이 있으며[1], 기계적 원인에 의한 진동으로는 회전부의 편심과 베어링 간극 등이 주된 요인으로 보고되고 있다[2][3]. 전자기적 원인에 의한 진동은 에어갭 편심에 의한 전자기력 불균형, 발전기 부하, 자속의 불균일 분포 등으로 알려져 있다[3].
이러한 가진이 수차의 고유진동수와 유사한 주기를 가질 때 발생되는 공진현상을 해결하기 위해 유동해석과 모형실험을 통해 수력학적 가진원을 예측하기도 하며[4] 실물 발전소에 설치된 압력계와 진동센서를 통해 이상진동 현상을 분석[4]하기도 하나 수차 설계단계에서부터 다양한 가진원을 고려하여 회피할 수 있는 설계를 수행 할 필요가 있다.
이를 위해 수차 구조물의 고유진동수를 파악해야 하며, 최근에는 전산해석분야 발달에 따라 수차 및 각종 터빈 구조물의 고유모드를 수치해석을 통해 계산한 다양한 연구들이 이루어지고 있다[5][6]. 그러나 수차는 가스터빈, 풍력터빈 등과 달리 수중에서 운용되는 장치로 공기 중에서의 고유진동수가 아닌 수중 고유진동수와 가진 주파수를 비교해야 한다. 일반적으로 유체에 잠겨있거나 접하고 있는 구조물은 유체에 의한 부가질량 및 감쇄 효과에 의해 공기 중에 있을 때에 비해 낮은 고유진동수를 나타낸다. 따라서 수차, 펌프 등 유체에 잠긴 상태에서 운용되는 장치들은 일반적인 공기 중 고유모드해석을 보완할 수 있는 방법을 사용해 분석해야만 한다.
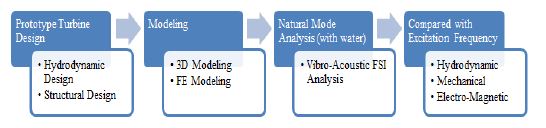
본 연구에서는 Figure 1과 같은 방법으로 6MW급 벌브수차의 스케일 모형인 100kW급 모형수차에 대해 수차 운용 특성을 고려하여 유체와 접한 상태의 고유진동수를 구했으며 이를 다양한 가진원 주파수와 비교하여 수차의 공진가능성을 저감할 수 있는 설계가 수행되었는지를 확인했다.
실물수차와 모형수차의 주요 제원은 Table 1과 같다.
2. 수치해석
2.1 음향-구조 연성해석
음향-구조 연성해석(Vibro-Acoustic FSI)은 유체를 매질로 삼아 전달되는 변위(진동), 압력(음향) 등이 구조물과 상호작용을 일으키는 현상을 분석하는 해석기법이다. 해석 도메인은 구조물과 음향매질(유체)로 구성되며, 이때 유체 도메인은 흐름이 발생하지 않고 진동을 전달하는 매질로만 가정된다. 따라서 유동해석에서 요구되는 동점성, 중력가속도 방향 등은 음향-구조 연성해석에의 유체에는 적용되지 않으며 유체 밀도와 유체 내 음속 만 물성치로 사용된다.
상기 해석기법을 사용해 진동 조건 하에서의 유체내 압력의 분포 및 구배, 음압(sound pressure level), 입사파/반사파/산란파/굴절파 등을 분석할 수 있으며 생성된 파의 감쇄/흡수에 관한 분석도 가능하다. 이러한 음향-구조 연성해석기법은 일반적으로 음향에 관련된 연구에 이용되나 본 연구와 같이 매질 유체를 물로 두고 가진원을 구조물로 설정하는 경우에는 수차나 펌프, 수중 이동체 등의 수중 구조물 고유진동수 계산에도 활용될 수 있다.
2.2 모델링 및 유한요소 모델생성
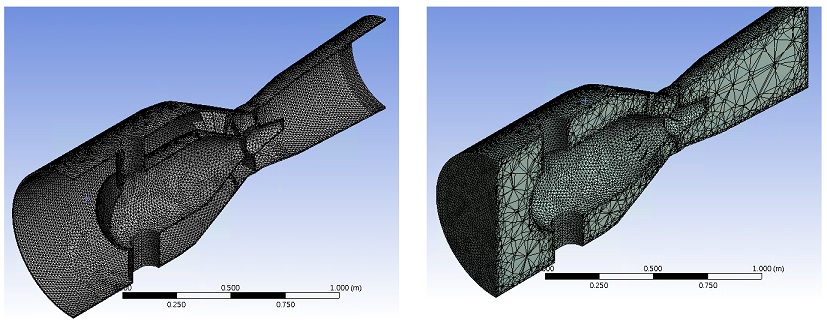
수중 고유진동 해석을 위해 상용 유한요소 프로그램인 ANSYS Workbench Design Modeler를 사용하여 벌브수차와 수차 내부 유체의 음향-구조 연성해석용 3D 모델링을 생성했다. 수차 모델링 범위는 벌브 케이싱 앞쪽에 위치한 입구단에서 드래프트 튜브가 끝나는 지점까지로 선정하고 상기 영역에 포함되는 수차와 유체를 함께 생성했다. 벌브 케이싱 내부에 장착되는 발전기와 축계 부분 모델링은 생략했으며 동일한 질량을 벌브 케이싱의 해당 부분에 부여했다. 그리고 유체와 접한 구조물의 고유진동 해석이 가능하도록 Vibro-Acoustic 해석모델을 만들었고 이를 위해 수차는 structure body, 유체는 acoustic body 로 구성했다. 이후 터빈 구조물에 SOLID187, 유체에 FLUID30 요소를 사용한 유한요소 모델을 생성했다. 음향-구조 연성해석에서 일반적으로 유체 부분 요소의 크기는 파장의 1/6~1/10 미만으로 권장되며[7], 파장의 크기는 다음과 같이 계산된다.
| (1) |
수중에서의 음속은 1500m/s 이며, 연구대상인 모형수차 구조물의 건조상태 1~6차 고유진동수는 555.49~765.24Hz 였다. 일반적으로 수중 고유진동수는 건조상태 고유진동수에 비해 낮게 나타나므로 수중 1~6차 고유진동수의 상한은 765.24Hz 이하일 것으로 추정할 수 있다. 이로부터 식(1)을 사용해 계산된 고유진동 파장은 6차 모드에서 1.96m 이며, 이때 유체 요소의 최대 크기는 파장의 1/10 이하인 0.196m를 만족해야 한다. 유체와 구조물 요소 크기로 15mm를 설정했으므로 해당 유한요소 모델은 고유진동으로 발생하는 진동 주파수를 처리하는데 충분한 수준의 요소 크기를 확보했다고 판단된다. 최종적으로 생성된 터빈과 유체 모델링의 총 절점은 525,982개, 요소는 349,118개이다. 각각의 물성치와 모델링은 Table 2, Figure 2와 같다.
2.3 경계조건 및 해석조건
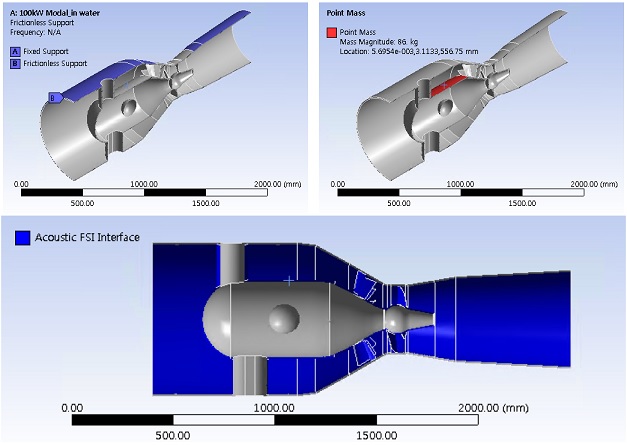
해석을 위해 벌브 수차와 유체에 각각의 경계조건을 부여했다. 벌브수차가 지반과 연결되는 부분은 fixed support 로 설정해 모든 자유도를 구속했고, 러너 부위는 실물 수차에서 수차 오버홀을 위한 공간이 설계된 부분이기에 구속을 부여하지 않았다. 입구/출구단 부분은 연결되는 수로용 배관과의 대칭성을 고려해 frictionless support 로 구속을 설정했다. 벌브 케이싱, 벌브 케이싱 상/하 지지부, 러너 블레이드 등 수차가 유체와 접하는 부분은 음향-구조 연성해석을 위해 acoustic FSI interface 로 설정하여 인접한 구조물 요소와 유체요소 노드를 연결했다. 음향-구조 연성해석은 구조물과 구조물의 진동을 전달할 수 있는 음향매질을 연결해주는 해석기법으로 다음과 같은 행렬로 구성된다.
| (2) |
[M], [C], [K], {u}, {p} 항들의 하첨자 S, F 는 각각 구조물과 유체를 나타내며, ρ0 는 매질이 되는 유체 밀도, [R] 은 구조물-유체(음향매질)를 연결해주는 연성행렬, u 와 p 는 각각 변위, 압력을 의미한다. 이는 일반적인 질량-감쇄-강성 항으로 이루어진 행렬식에 구조물과 유체간 연성성분인 [R] 행렬이 추가된 것으로 연성효과는 질량부분과 강성부분에만 작용하며 감쇄부분에는 작용하지 않는다는 것을 보여준다. 음향-구조 연성해석을 통해 구조물에서 발생하는 변위는 인근에 위치한 노드의 유체 요소에 전달되어 압력으로 작용하고 유체는 접촉하는 구조물에 부가질량으로 작용하게 된다.
이상과 같은 모형 벌브수차의 경계조건을 Figure 3에 나타냈다. 비교를 위해 수차에서 유체를 제외한 통상적인 고유모드 해석을 병행했으며, 이 경우 유체영역과 음향-구조 연성 경계조건을 제외하고 해석을 수행했다.
3. 해석 결과
3.1 건조상태 고유진동해석결과
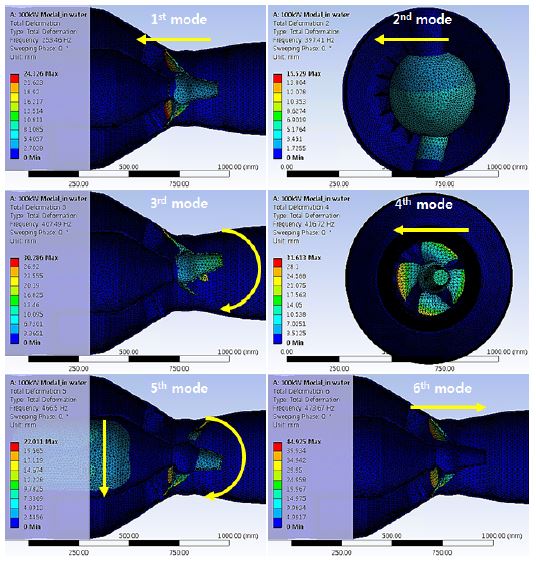
해석결과 유체를 제외한 상태에서는 1~6차 고유진동수가 555.48~765.24Hz 범위에 있었다. 1차 모드는 러너 블레이드부가 555.48Hz 로 좌우방향 진동을 보였으며 2차 모드는 러너 블레이드부가 570.57Hz 로 상하방향 진동을 보였다. 3차 모드는 벌브 케이싱부가 589.55Hz 로 좌우방향 진동을 보였으며 4차 모드는 러너 블레이드부와 벌브 케이싱부가 706.88Hz 로 전후방향 진동을 보였다. 5차 모드는 730.66 Hz 로 러너 블레이드부가 전후방향, 벌브 케이싱부가 상하방향 진동을 보였으며 6차 모드는 러너 블레이드 날개가 2매씩 교차하여 765.24Hz 로 전후방향 진동을 보였다. Table 3에는 건조 상태와 수중에서의 1~6차 고유진동수를 비교했고 Figure 4에는 건조 상태의 모드별 형상을 나타냈다.
3.2 수중 고유진동해석결과
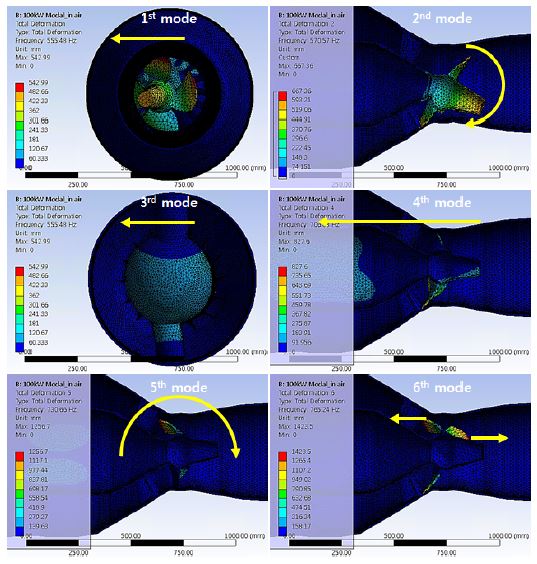
해석결과 수중에서는 1~6차 고유진동수가 253.46~ 473.67Hz 범위에 있었다. 1차 모드는 러너 블레이드 날개가 253.46Hz 로 전후방향 진동을 보였으며 2차 모드는 건조 상태의 3차 모드와 유사하게 벌브 케이싱부가 397.41Hz 로 좌우방향 진동을 보였다. 3차 모드는 건조 상태의 2차 모드와 유사하게 러너 블레이드부가 407.49Hz 로 상하방향 진동을 보였으며 4차 모드는 건조 상태의 1차 모드와 유사하게 러너 블레이드 날개가 416.72Hz 로 좌우방향 진동을 보였다. 5차 모드는 러너 블레이드부와 벌브 케이싱부가 466.5Hz 로 수직방향 진동을 보였으며 6차 모드는 러너 블레이드 날개가 473.67Hz 로 전후방향 진동을 보였다. Figure 5에는 수중 모드별 형상을 나타냈다.
4. 결과 분석
4.1 정격 운전 주파수 및 깃통과 주파수와 비교
해석으로 얻어진 모형 벌브수차 수중 고유진동수를 수차의 정격 운전 주파수(Rated Operational Frequency) 및 깃통과 주파수(Blade Passing Frequency, BPF)와 비교했다. 수차 운전 주파수는 주로 회전부 질량 불평형, 베어링 이상 등의 기계적인 원인으로 발생하는 가진 주파수로 공진회피설계시 1차적으로 고려되는 가진이다. 깃통과 주파수는 수차, 펌프 등의 회전기계에서 동익을 통과하는 유체의 압력변화에 따라 발생하는 수력학적 가진으로 운전 주파수에 날개수의 배수로 나타난다. 모형 수차의 경우 정격운전속도인 1200rpm으로부터 발생하는 회전 주파수는 20Hz 이며 러너 블레이드 4개로부터 발생하는 깃통과 주파수는 80Hz 이다.
| (3) |
모형 수차 수중 고유진동수를 정격 운전 주파수와 비교할 때 1267~2368% 마진이 확보되었으며 깃통과 주파수에 대해서는 317~592% 확보되어 공진 회피를 위해 권장되는 주파수 분리 범위인 ±20%를 충분히 벗어났다. Table 4에는 1~6차 고유진동수와 운전 주파수, 깃통과 주파수를 비교했다.
4.2 무부하 운전 주파수 및 깃통과 주파수와 비교
해석에서 얻어진 모형 벌브수차 수중 고유진동수를 수차 무부하운전(Runaway)주파수 및 깃통과주파수와 비교했다. 수차의 전기적 부하가 차단된 상태에서 운전되는 무부하 운전은 회전속도 상승 범위를 정격운전속도의 200% 정도로 가정한다. 따라서 모형수차의 무부하 회전속도를 1200rpm 의 200%인 2400rpm 으로 가정했고, 이로부터 발생하는 회전 주파수를 40Hz, 깃통과 주파수를 160Hz 로 가정했다.
| (4) |
수차의 수중 고유진동수를 무부하 운전주파수와 비교할 때 634~1184% 마진이 확보되었으며 깃통과 주파수에 대해서는 158~296% 가 확보되어 공진 회피를 위해 권장되는 주파수 분리 범위인 ±20%를 충분히 상회했다. Table 5에는 1~6차 고유진동수와 무부하 운전주파수, 깃통과 주파수를 비교했다.
4.3 기타 가진원에 대한 분석
수차 운전시 발생하는 가진원으로는 회전주파수와 깃통과주파수 외에도 특정 부하 영역에서 드래프트 튜브부에 발생하는 와류에 의한 VIV, 수차 동익과 정익 사이에서 발생하는 RSI(Rotor-Stator Interaction), 러너 블레이드 후방에서 발생하는 칼만 와류, 특정 부하영역에서 발생하는 캐비테이션 등의 수력학적 진동이 있으며 발전기에서 발생하는 전자기적 진동도 있다. 다만, RSI는 프란시스 수차와 같이 동익과 정익 간격이 매우 좁은 수차에서만 발생하기에 벌브수차를 대상으로 한 이 연구에서는 제외했다. 또한 유속과 유로 내부의 구조물 단면 형상에 따라 주파수가 결정되는 칼만 와류는 블레이드 트레일링 엣지부가 cut off 된 형상에서 주로 발생하는 것으로[8] 트레일링 엣지부가 곡면으로 이루어진 현재 러너 블레이드 설계에서는 미미한 수준이 발생할 것으로 예상되어 가진원 분석에서 제외했다.
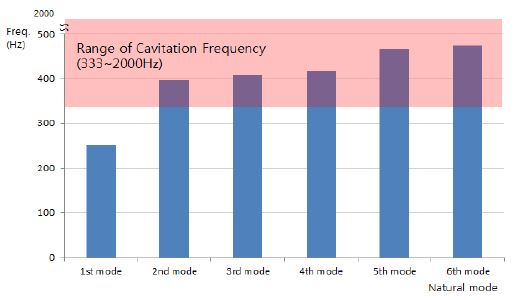
블레이드부 캐비테이션에 의한 진동은 통상적으로 수차 크기 및 회전수에 관계없이 333~2000Hz 대역에서 발생하는 것으로 알려져 있기에[2] 모형 수차의 수중 2~6차 고유진동수가 이에 해당될 수 있다. 따라서 2차와 5차 모드의 경우 벌브 케이싱부 좌우/상하방향 진동에 대응하기 위해 케이싱 상/하부 지지구조물 강성을 보강하고 3, 4차 모드의 경우 러너 블레이드부의 수평/수직 방향 진동에 대응하기 위한 축계 강성을 보강할 필요가 있다. 다만 실물수차에서는 수차 크기 증가에 따라 고유진동수가 이보다 낮아질 가능성이 있기에 실물 수차의 고유진동수는 캐비테이션 주파수와 분리될 수도 있다. Figure 6에는 수차의 1~6차 고유진동수와 캐비테이션 주파수 범위를 비교했다.
수차의 부분부하영역에서 발생하기도 하는 VIV 는 모형실험 또는 유동해석을 통해 발생여부를 정확하게 판단할 수 있기에 본 연구에서는 통상적으로 수차회전주파수의 0.2~0.4X 로 알려진 범위 주파수[8]를 가정하여 비교했다. VIV 발생시 예상되는 주파수 범위는 다음과 같다.
| (5) |
비교 결과 모형 수차의 1~6차 수중 고유진동수는 VIV 하한값과 비교할 때 6337~11842%, 상한값과 비교할 때는 3168~5921% 로 충분히 분리되어 있었다. Table 6에는 1~6차 고유진동수와 VIV 주파수 범위를 비교했다.
전자기적 가진원들에 대한 공진 가능성을 확인하기 위해 발전기 부하에 의한 가진과 에어갭(Air Gap) 불균형에 의한 가진 주파수를 각각 비교했다. 교류 발전기의 경우 부하에 의한 진동은 전류주파수의 2배로 나타나므로 우리나라의 전류주파수인 60Hz에서 발생되는 진동은 120Hz 이다. 회전자 또는 고정자의 편심으로 인해 회전자-고정자 간극인 에어갭 불균형으로 발생하는 진동은 발전기 회전수와 극수의 곱으로 나타나기에 본 연구에서 분석하는 모형 수차에서 해당 진동이 발생할 경우 4극에 따른 80Hz 주파수로 나타날 것으로 예상된다.
| (6) |
전자기적 가진원들에 대해 모형 수차의 1~6차 수중 고유진동수는 발전기 부하 주파수와 비교할 때 211~395%, 에어갭 불균형 주파수와 비교할 때는 317~592% 로 충분히 분리되어 있었다. Table 7에는 1~6차 고유진동수와 전자기적 가진 주파수를 비교했다.
5. 결 론
본 연구에서는 벌브수차의 공진회피설계 여부를 확인하기 위해 음향-구조 연성해석기법을 사용하여 모형수차의 수중 고유진동수를 도출했고, 이를 기계적, 수력학적, 전자기적 가진 주파수와 비교했다.
- 1) 정격 운전 주파수와 비교한 결과 1267~2368% 마진이 확보되었고 깃통과 주파수와 비교했을 때는 317~592% 가 확보되었다.
- 2) 무부하 운전 주파수와 비교한 결과 634~1184% 마진이 확보되었고 무부하 운전시의 깃통과 주파수와 비교했을 때는 158~296% 가 확보되었다.
- 3) 캐비테이션 주파수와 비교했을 때는 2~6차 고유진동수가 해당 주파수 범위에 포함될 수 있는 것으로 나타났으며, 해당 모드 형상에 해당하는 부위를 참고하여 벌브 케이싱 상하부 지지구조물과 축계 부분 강성을 보강할 필요가 있다. 다만 실물수차 스케일에서는 고유진동수가 감소할 것으로 예상되어 캐비테이션 주파수 범위를 벗어날 가능성이 있다.
- 4) VIV가 발생할 수 있는 범위의 상한/하한 주파수와 비교한 결과 주파수 상한값과 3168~5921%, 주파수 하한값과 6337~11842% 분리되어 있었다.
- 5) 전자기적 가진원들과 비교했을 때는 발전기 부하 주파수와 211~395%, 에어갭 불균형 주파수와 317~592% 분리되어 있었다.
- 6) 모형수차에 사용된 수중 고유진동해석 및 가진주파수 분석 절차는 향후 벌브수차를 비롯한 다양한 수차 설계시에 활용할 수 있을 것이다.
Acknowledgments
본 연구는 2016년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. 20163010060340)
Author Contributions
Conceptualization, W. Kwon and J. H. Kim; Methodology, W. Kwon; Software, K. Li; Validation, W. Kwon and J. H. Kim; Formal Analysis, K. Li and T. G. Hwang; Investigation, K. Li; Resources, W. Kwon and K. Li; Data Curation, W. Kwon; Writing—Original Draft Preparation, W. Kwon; Writing— Review & Editing, W. Kwon; Supervision, J. H. Kim; Project Administration, J. H. Kim; Funding Acquisition, T. G. Hwang;
References
- J .W. Lee, D. G. Byun, and E. T. Kim, “Noise and vibration analysis in hydro power plant,” Proceedings of the Korean Institute of Electrical Engineers Conference, pp. 516-520, 1997.
- B. J. Lee, Vibration and Maintenance Handbook, Incosys, pp. 401-482, 1998 (in Korean).
-
R. K. Mohanta, T. R. Chelliah, S. Allamsetty, A. Akula, and R. Ghosh, “Sources of vibration and their treatment in hydro power stations - A review,” Engineering Science and Technology, an International Journal, vol. 20, no. 2, pp. 637-648, 2017.
[https://doi.org/10.1016/j.jestch.2016.11.004]

- Y. Fang, S. Yoan, J. Li, J. Yu, J. Zhang, and D. Peter, “Evaluation of the hydraulic resonance in turbine mode of a medium-head pump-turbine,” Journal of Vibration Engineering & Technologies, vol. 5, no. 5, pp. 451-466, 2017.
- F. Lafleur, V. H. Vu, and M. Thomas, “Case study of operational modal analysis (OMA) of a large hydroelectric generator,” 29th Seminar on Machinery Vibration, Canadian Machinery Vibration Association, St. John NF, Canada, 2011.
- S. J. Ryu and H. C. Ha, “Modal analysis and testing of a high head pump/turbine runner,” Transactions of the Korean Society for Noise and Vibration Engineering, vol. 8, no. 6, pp. 1062-1068, 1998.
- W. Desmet and D. Vandepitte, Finite Element Modeling for Acoustics, LMS Engineering Innovation, 2005.
-
N. Thomareis and G. Papadakis, Effect of trailing edge shape on the separated flow characteristics around an airfoil at low Reynolds number: A numerical study, PHYSICS OF FLUIDS, vol. 29, no. 1, 014101-01-014101-17, 2017.
[https://doi.org/10.1063/1.4973811]