알루미늄 헬리데크 최종강도 거동에 영향을 미치는 변수에 대한 고찰
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
최근, 조선 및 해양 구조 분야에서 친환경 소재를 적용한 각종 사례가 연구되고 있다. 특히, 알루미늄 합금 소재의 적용성 연구가 활발하게 진행되고 있다. 알루미늄 합금은 질량에 비교해 높은 강성과 강도를 갖고 있으며, 헬리데크, 플레어 타워, 플랫폼 및 거주구등에서 많이 적용되고 있다. 이 중에서도 헬리데크의 경우에는 헬리콥터의 이/착륙 시 중량 및 충격하중에 상시 노출되기 때문에, 상세한 구조 안전성 검토가 필요하다. 본 연구에서는 알루미늄 합금 갑판의 모형화 기법에 따른 압축 최종강도 특성을 분석하기 위하여, 선형 및 비선형 해석방법에 따른 거동 분석을 수행하였다. 이때 사용한 요소는 셀과 솔리드 요소이며, 실제 형상의 반영 유/무에 따른 구조 강도 영향도 검토하였다. 초기항복 하중 및 최종강도 하중은 요소 크기가 25mm 이상의 조건에서 유사한 결과를 나타내고 있으며, 솔리드요소 적용한 모델링 시 라운드 형상의 반영이 필요하다. 이 연구의 주요 내용은 향후 유사 연구를 수행하는 구조 엔지니어에게 판단의 좋은 자료가 될 것으로 생각한다.
Abstract
Recently, various examples of eco-friendly materials have been used to study their potential applications in naval and offshore industries. In particular, the applicability of aluminium alloy materials has been actively studied. Aluminium alloys have high rigidity and strength compared with their mass, and are widely applied in helideck structures, flare towers, platforms, and living quarters. In the case of helideck structures, structural and safety considerations are needed because the helicopter is constantly exposed to the weight and impact load when the helicopter is landing or take-off action. In this study, to analyze the ultimate strength characteristics of the aluminium alloy deck according to the modelling technique, the strength analysis depends on linear and nonlinear analysis methods was performed. The elements used in this study are shell and solid elements, and the effect of structural strength according to geometric shape is reflected. The initial yielding load and ultimate load converges at an element size of 25 mm or more, and a round shape is required for solid modelling. The results of this study will serve as good reference data for structural engineers performing similar studies in the future.
Keywords:
Aluminium alloy materials, Helideck structures, Ultimate strength, Nonlinear analysis, Shell modeling키워드:
알루미늄 합금재료, 헬리데크 구조, 최종강도, 비선형해석, 셀 모델링1. 서 론
2019년 국내외 조선 및 해양플랜트 경제 및 산업전망[1]에 의하면, 조선 산업은 폐선증가에 따른 대체수요 등이 기대되나, 2018년 세계시황 성장 대비 국내 수주 증가폭 확대에 따른 기저효과로 선박 수주는 약 2% 감소한 214억 달러를 수주할 전망이다. 해양플랜트 산업은 유가 상승에 따른 투자심리 개선과 점진적 수요확대로 해양가스설비와 석유생산설비 등 3-4기 수주가 가능할 것으로 전망하고 있다. 최근, 조선 및 해양 구조 분야에서 친환경 소재를 적용한 각종 사례가 연구되고 있으며, 알루미늄 합금 소재의 해양분야 적용성 연구가 활발하게 진행되고 있다[2]. 본 연구에서는 알루미늄 헬리데크의 최상판을 구성하고 있는 팬케이크의 모델링 기법 차이에 의한 압축 최종강도 특성을 분석하였다. 하중에 의한 응력 및 붕괴 거동을 평가하기 위하여, 선형 및 비선형 해석방법을 적용하였다. 이때 사용한 요소는 셀과 솔리드 요소이며, 실제 형상의 반영 유/무에 따른 구조 강도 영향도 검토하였다.
본 논문에서는 해양구조물에서 필수적으로 사용하고 있는 알루미늄 헬리데크 상판 구조물에 대한 상세 구조 강도 평가 시 엔지니어가 필수적으로 고려해야 하는 변수를 발췌하고, 상세 구조해석을 통한 검증을 통하여 그 경향을 연구하였다. 이와 관련된 기존의 선행연구를 다음과 같이 요약하였다.
R. Chacon et al. [3]은 압출로 생산된 알루미늄 거더의 휨 거동에 대해서 실험을 수행하여, 구조 응답 특성을 분석하였으며, 이 결과를 수치 시뮬레이션과 비교 검증을 하여 설계에 적용할 수 있는 최종강도 예측 경험식을 제안하였다.
J. H. Chun [4]는 알루미늄 헬리데크의 구조적 안전성을 검토하기 위하여, 헬리콥터 충돌 위치 및 하중의 크기에 따른 구조 응답을 동적해석을 통하여 연구하였다. 일반적인 동적 효과를 고려하기 위하여, 규칙에서 권고하는 안전계수를 고려하고 있으나, 본 연구에서는 실제 발생 가능한 불시착 시나리오를 산정하고, 그에 따른 동적 응답 계수를 시뮬레이션을 통하여 추정하였다.
B. M. Kim et al. [5]은 허용 응력 기준을 만족하도록 설계된 캔틸레버형 헬리데크의 비선형 좌굴의 안전성을 평가하기 위해 헬리데크의 설계 조건들과 연구 결과 평가를 위한 기준은 DNV(Det Norske Veritas)의 OS-E401 [6]과 CAA(Civil Aviation Authority)의 CAP-437 [7]의 규정을 참조하였으며, 동적안전성을 평가하기 위하여 ANSYS Mechanical APDL를 사용하였다. 설계 착륙 하중에 대한 선형 또는 비선형 좌굴이 발생할 때 가해진 착륙하중의 비를 임계 설계하중계수로 산정하여 캔틸레버형 헬리데크 설계의 구조적 안전성을 검증하였다.
J. S. Jo et al. [8]은 알루미늄 헬리데크에 사용되는 매립형 고박장치의 구조 안전성에 대한 검토를 진행하였다. 사용된 재료는 알루미늄 합금 6082-T6를 적용하였고, 주요 하중을 지탱하는 Round bar는 고강도의 Duplex stainless steel 329 재료를 적용하였다. 기존의 mild steel 혹은 SUS 316으로는 변경된 국제규정에 부합하는 구조 강도를 만족하지 못하기 때문이며, 알루미늄과의 이종재료 부식문제 또한 고려하였다. 헬리콥터 고박 시 발생할 수 있는 다양한 하중 시나리오를 검토하였으며, 개발품의 구조 강도가 국제규정에 만족함을 수치해석을 통하여 검증하였다.
Y. Q. Wang et al. [9]은 한변 고정과 한변 핀 조건을 갖는 알루미늄 I 단면을 갖는 기둥 부재의 압축 좌굴 거동에 대해서 실험 및 수치계산을 수행하였다. 총 11개의 시험을 수행하였다. 현존하는 4가지 표준(유럽, 중국, 미국, 호주)과의 비교 평가를 하였으며, 4가지 설계 조항은 상대적으로 보수적인 압축 좌굴 강도 값을 예측하였다. 특히, 알루미늄의 가공경화 특성에 대해서는 실험치와 많은 차이를 확인하였다.
Z. X. Wang et al. [10]은 I형 단면과 직사각형 단면을 가진 기둥 부재의 압축 좌굴 거동을 평가하였다. 총 7개의 시험편을 구성하였으며, 모두 휨 좌굴에 의해서 붕괴함을 확인하였다. 현재의 설계 기준과의 신뢰성 분석을 위하여, 총 180 경우에 대한 변수 변화 시리즈해석을 ANSYS를 활용하여 수행하였다. 미국과 중국 알루미늄 설계 기준은 실험 및 시뮬레이션 결과 대비 다소 보수적인 평가를 하였으며, 이를 개선하기 위하여 새로운 평가식을 제안하였다.
따라서 본 연구에서는 선행연구 및 알루미늄 구조설계 기준(국제 지침)에서 언급하지 않는 상세구조해석을 통한 구조해석 시 결과에 영향을 미칠 수 있는 변수들에 대한 자세한 분석을 통하여 합리적인 평가기준안을 제시하였다. 본 연구를 통하여 도출된 주요 결과는 향후 구조해석 시 가장 중요한 모델링 기법 및 평가 방법에 관련한 기초적인 자료로 유용하게 활용될 것으로 판단된다.
2. 알루미늄 헬리데크
2.1 알루미늄 헬리데크 단면
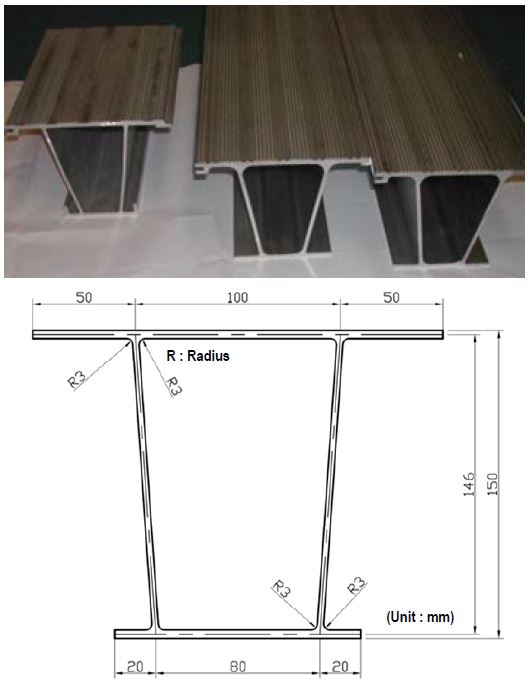
해양구조물 시장의 급성장과 맞물려서 알루미늄 헬리데크 시장도 점점 커지고 있으며, 주요 원천기술은 유럽(네델란드, 덴마크, 노르웨이)국가에서 보유하고 있다. 최근, 알루미늄 헬리데크에 대한 관심이 증가하면서 국내 대형조선사를 중심으로 관련 기술에 대한 자립화 및 제품개발에 노력을 기울이고 있다. 본 연구에서 대상으로 하는 알루미늄 헬리데크의 경우, 헬리콥터의 자유로운 이/착륙을 유도하기 위하여, 플랫폼의 모서리 위치에 주로 설치되어 있다. Figure 1은 대표적인 해양구조물에 설치된 알루미늄 헬리데크와 헬리콥터의 착륙에 대한 예시 자료이다.
Offshore aluminium helideck
Figure 2에서는 본 논문의 연구대상인 알루미늄 헬리데크를 구성하고 있는 단면구조를 나타내고 있다. 한 개의 헬리데크를 구성하기 위해서는, 수십 개의 단면구조를 조립하여 구성하며, 주요 연결부위는 횡 방향 끼워 맞춤 방법을 이용하며, 하부 빔 구조와는 볼팅 혹은 클램핑 방식을 이용한다. 이는 알루미늄 합금 자체가 용접작업에 의해서 아주 취약하며, 데크 단면의 두께가 상대적으로 얇기 때문이다.
Aluminium deck profile and dimension
본 연구에서 사용하고 있는 알루미늄 합금 6082-T6에 대한 물성값 정보를 Table 1[11]에서 나타내고 있다.
Material properties of the aluminium extruded profile
2.2 해석기법
본 논문에서는 유한요소법(Finite Element Method)을 이용한 탄성 및 비선형 대변형 거동 해석을 통한 알루미늄 헬리데크 단면의 구조 강도 평가를 주로 다루고 있다. 비선형 해석기법으로는 안정적이고 신뢰적인 결과값 도출이 가능한 Arc-length method를 적용하여 해석을 수행하였다. 위 방법은 하중형증분법과 변위형증분법을 동시에 제어하며, 급작스러운 변위 거동이나 하중 거동이 일어날지라도 수치적 해석이 가능하며 해석제약조건에 큰 영향을 받지 않는 방법이다. 그러나, 실험적인 접근에서는 이 방법을 적용할 수가 없으며 오직 수치적 접근에 의해서만 적용할 수가 있다. 본 논문에서 채택한 비선형 좌굴해석 기법인 Arc-length method는 초기 원호의 해석반경을 설정해주면 비선형 좌굴해석 메커니즘으로 잘 알려진 Newton Raphson Method와 조화를 이루어 각 증분 구간별로 사용자가 설정해놓은 반복 수만큼 계산을 수행하여 두 가지의 경로에서 교차하는 점들의 평균점만을 찾아가는 방법이라고 할 수가 있다. Arc-length method에서는 증분 파라미터로서 하중-처짐 곡선의 길이를 증분 시키며 하중제어와 변위 제어를 동시에 사용, 동시 제어를 가능하게 하여 응답이 완만하거나 급작스러운 분기점(Bifurcation point)이 존재하지 않는 경우 가장 적합한 방법이며, 본 연구의 해석에 적용하고 있다.
2.3 해석모델 및 조건
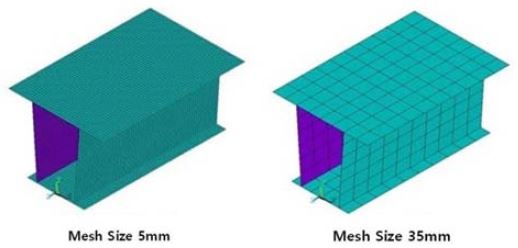
Figure 3에서는 셀요소를 적용하고, 요소의 크기를 5mm에서 35mm까지 5mm 간격으로 변화시킨 총 7개의 해석모델 일부를 나타내고 있다. 요소는 ANSYS 프로그램[12]에서 제공하고 있는 4 절점 사각형 요소이며, 선형/비선형 및 상태변화 비선형에서도 사용할 수 있으며, 한 개의 절점에는 6개의 자유도를 표현할 수 있다.
Shell model depend on the mesh size
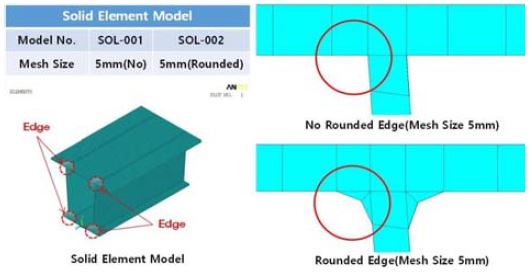
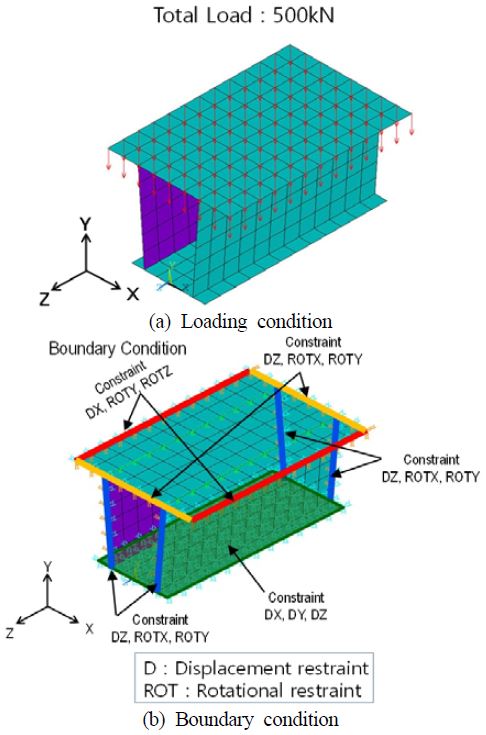
Figure 4에서는 20 절점 솔리드요소를 적용한 단면의 모델링을 나타내고 있으며, 요소의 크기는 실제 두께를 반영하여 5mm로 고정하였다. 단면에 충격하중이 작용할 경우, 응력집중이 발생하기 쉬운 수직과 수평부재의 교차점에 대하여 실제 압출 실물의 형상을 반영하기 위하여 라운드 형상 모델링을 추가로 고려하여, 일반적인 모델링에 의한 결과와 비교하였다. 또한 Figure 5에서는 해석에 적용된 하중 조건 및 경계조건을 나타내고 있다. 비선형 붕괴 거동을 예측하기 위해서는 최종강도와 그 이후 거동을 명확하게 확인할 수 있는 최대값이 필요하며, 이에 본 연구에서는 500kN을 적용하였다.
Solid model depend on the edge modeling shape
Loading and boundary condition
이 하중은 균일하게 한 개의 데크 면적에 전체하중으로 분포시켰다. 이러한 이유는 해석에서 고려한 헬리콥터 (Sikorsky –S92)의 이/착륙 시 타이어의 접지 면적이 가로/세로가 약 250mm이기 때문이다. 경계조건은 데크 단면의 폭 방향 및 길이 방향은 연속거동조건을 고려하기 위하여, 대칭 조건을 적용하였으며 바닥 면은 볼트 및 클램프로 고정되어 있으며, 3자유도 변위(x, y, z)를 고정하였다.
2.4 압출 시 발생하는 초기부정 효과
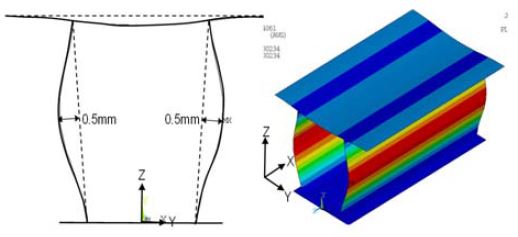
알루미늄 헬리데크를 구성하는 압출 재는 원자재를 원하는 형상으로 생산하기 위하여, 압출용 금형을 활용하고 있다. 이 과정에서 압출 재의 생산공차가 발생하며, 연구에서 개발하고자 하는 단면에는 수직방향 웨브에서 최대 0.5mm를 Figure 6과 같이 고려하였다.
Extrusion tolerance and shape
압출에 의한 공차의 크기 및 형상은 압출 업체로부터 제공받은 정보이며, 헬리데크 팬케이크 상면에 압축하중이 주요하기 때문에, 생산공차를 포함한 해석모델을 적용하여 시리즈해석을 수행하였다.
3. 유한요소해석을 통한 강도검증
3.1 패치 하중 선정 및 유한요소해석
헬리데크를 설계하기 위해서는 헬리콥터의 사양을 결정해야 하며, 본 연구에서는 해양플랫폼에서 가장 빈번하게 사용하는 기종인 Sikorsky S-92를 선택하였다. 아래의 데이터는 이 기종에 대한 주요 제원 및 일반배치도를 Table 2와 Figure 7에 나타내고 있다. 해석에 사용된 유한요소해석프로그램은 ANSYS V.18로서 구조해석 라이선스는 Structural Solver을 이용하였다. 주로 선형 및 비선형해석에 사용되며, 다양한 구조 강도 해석 시 활용되고 있다. 유한 셀 요소는 shell 181을 적용하였으며, 얇은 두께부터 적당히 두꺼운 판으로 구성된 구조 강도 해석에 적합하다. X, Y, Z 변위와 회전을 각 노드에서 제어할 수 있는 전통적인 4노드를 갖는 요소이다. 요소에서 사용되는 형상함수는 대변형 및 실제 응력 측정을 기반으로 하고 있으며, 요소 기구학은 멤브레인 변형을 허용하고 있다. 3차원 솔리드 요소는 186을 적용하였고, 20개의 노드를 갖고 있다. 각 노드에는 변위 X, Y 그리고 Z 변위를 표현하며, 소성, 초탄성, 대변형 해석에 적합하다.
General characteristics of Sikorsky S-92 helicopter
Sikorsky S-92 helicopter
3.2 패치 하중 적용에 따른 붕괴 거동 (셀 요소)
수치계산에 사용된 해석모델의 메쉬 크기에 따른 유한요소의 개수를 Table 3에서 나타내고 있다. 솔리드요소를 사용한 경우, Round shape를 구현하기 위하여, 요소의 크기를 5mm, 10mm 조건으로만 검토가 되었다.
Total number of elements according to element types
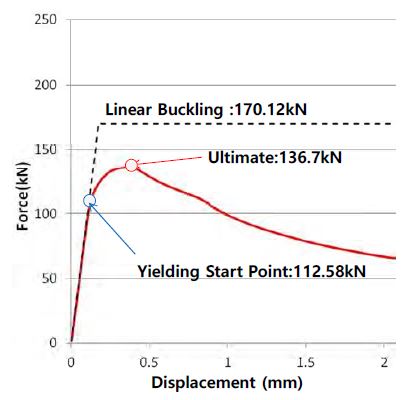
지정된 헬리콥터의 이/착륙에 의한 패치 하중 전달 시 알루미늄 헬리데크에서의 좌굴을 포함한 붕괴 거동 해석 결과를 하중과 변위 관계로 Figure 8에 나타내고 있다. 요소의 크기는 가장 작은 5mm를 모델링에 반영하였다. 선형 고유치 좌굴해석을 통하여 구해진 하중 값을 점선으로 표기하였으며, 비선형 좌굴 및 최종강도 결과는 증분/수렴 해석을 통하여 도출하였다. 초기항복은 112.58kN이 작용하는 시점에 상판과 수직부재가 만나는 경계에서 발생하며, 하중 크기 증가에 따라서 길이 방향으로 유사한 분포 특징을 나타낸다. 초기항복이 발생한 시점에서 곧바로 헬리데크 단면의 최종강도가 결정되며, 최종강도 이후 면내 강성 감소가 크게 나타난다. 이러한 특징은 일반적인 탄소강과 달리 알루미늄의 경우 연신율이 크기 때문이다.
A comparison of the force and displacement using shell model with 5mm elements under impact load
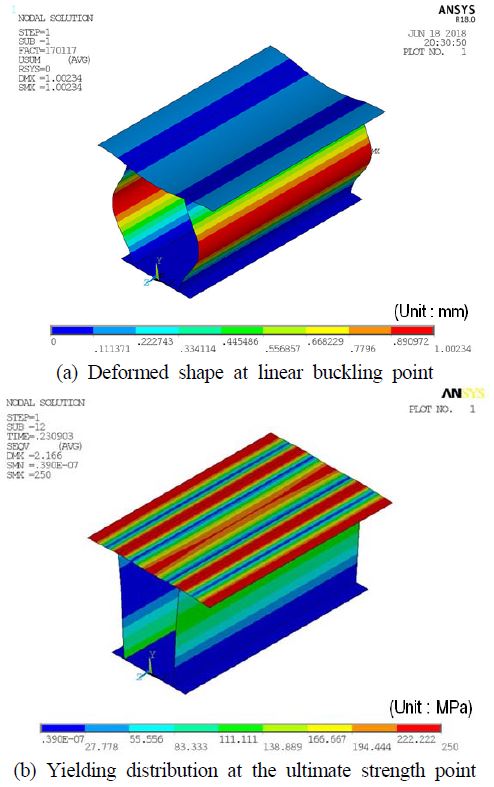
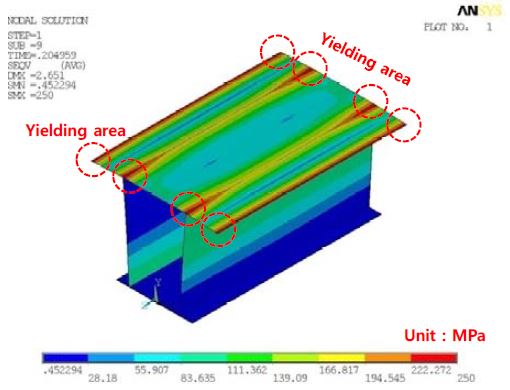
Figure 9에서는 고유치 좌굴해석을 통한 좌굴 변형 모드를 Figure 9 (a)에서 나타내며, 최종강도 상태에서 항복 응력 분포를 Figure 9 (b)에 정리하였다. 패치 하중에 따른 압축 하중을 주로 담당하는 수직부재에서 좌굴이 발생하는 경향이며, 최종강도에서의 항복 응력은 데크 상면에 넓게 분포되고 있다.
Deformed shape and yield distribution of shell model with 5mm elements under impact load
Figure 10에서는 요소 크기를 35mm를 적용한 셀 모델링에 의한 붕괴 거동을 하중과 변위로 나타내고 있다. 요소 크기가 증가함에 따라서, 탄성 좌굴응력과 최종강도는 증가하였으며, 초기항복 하중은 감소하였다. 만약 초기항복 하중이 설계 인자였다면, 요소의 크기에 변화에 따라서 결과는 민감하게 나타남을 확인할 수 있다. 요소 크기 5mm에 비해서 최종강도 상태에서의 헬리데크 상면에서의 항복 응력 분포는 다른 경향을 Figure 11에서 나타내고 있다. 상면과 교차하는 수직부재 영역에서 국부적인 항복이 발생하고, 상단면 전체적으로 항복 응력이 분포하지는 않는다.
A comparison of the force and displacement using shell model with 35mm elements under impact load
Yielding distribution of shell model with 35mm elements under impact load
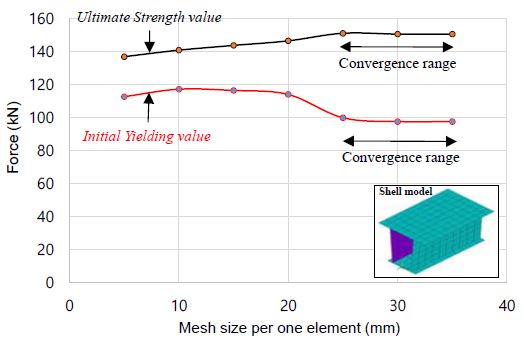
Figure 12에서는 셀 요소를 적용한 유한요소모델에서의 하중을 세로축에 표현하고, 요소의 크기 변화를 가로축에 표기한 결과를 초기항복 하중과 최종강도 하중으로 구분하여 비교하고 있다. 초기항복 하중은 요소의 크기가 작을수록 높게 평가하며, 요소의 크기가 25mm 이상의 조건에서 일정한 최대하중으로 근접하고 있다. 최종하중 분포의 경우, 요소의 크기가 커질수록 점진적으로 증가하는 경향을 나타낸다. 이는 일반적인 유한요소 모델링을 이용한 선형 구조 강도 해석 시 요소의 조밀도에 따른 강도분포 결과와는 다르다. 본 논문에서는 해당 모델의 안정적인 비선형 최종강도 시점의 하중을 예측하기 위한 요소 크기를 25mm 결정하였다. 이러한 특징은 현재의 구조모델의 크기 및 형상과 밀접한 관련이 있으며, 위 조건들이 변경될 때는 요소 크기 변화에 따른 변화를 확인한 후, 시리즈해석을 수행해야 한다. 구조엔지니어링 분야의 종사자들은 이러한 사항이 강제규제사항이 아니기 때문에, 적당한 요소 크기를 임의 선택하는 경우가 많다.
A comparison of the average stress and element size according to yielding and ultimate strength
3.3 패치 하중 적용에 따른 붕괴 거동 (솔리드 요소)
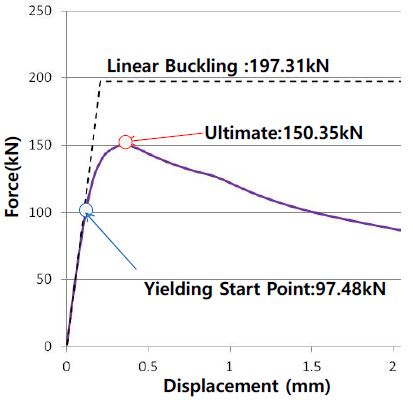
데크유닛의 상세한 형상 구현에 따른 붕괴 거동을 예측하기 위하여, 3차원 솔리드 요소를 적용하고, 데크 상면과 수직부재가 만나는 곳의 상세 모델링을 적용하면서, 라운드 형상 반영 유/무에 따른 하중과 변위 결과를 Figure 13 (a)와 Figure 13 (b)에 나타내고 있다.
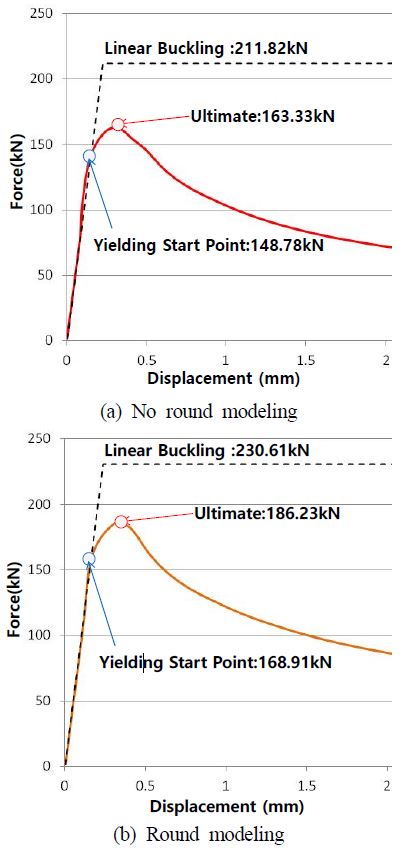
A comparison of the force and displacement using solid elements according to the modeling under impact load
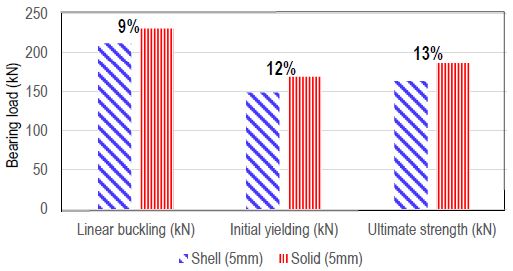
선형 고유치 좌굴해석을 통하여 구해진 임계 좌굴하중 값은 초기항복 하중과 최종강도 하중 값보다 크게 도출되고 있다. 이는 압출 시 발생할 수 있는 공차 0.5mm에 대한 영향 및 재료의 비선형 거동을 고려하지 않았기 때문이다. 초기항복 하중은 라운드 형상을 반영한 경우가 약 12% 높게 평가하며, 최종강도 하중은 13% 높았다. 이러한 원인은 가장 응력집중이 크게 발생하는 곳에서 모서리 형상에 따라서 응력집중 가속화율이 다르게 나타나기 때문이다. 압출에 의한 헬리데크 단면의 경우 코너부의 응력집중 완화를 위하여 모서리부에는 일정 곡률을 필수적으로 설계 시 반영하고 있으며, 구조 강도 검토 시에도 이러한 영향을 반영해야만 실제의 구조 거동을 정확하게 예측할 수 있다. 연결부에 대한 피로강도 예측 시에는 실제의 형상을 구현해야 하며, 일반적으로 두께만큼의 크기로 요소 분할을 해야 한다.
모델링 요소의 차이에 의한 선형좌굴하중, 초기항복하중 그리고 최종강도 하중에 대한 비교 결과를 Figure 14에 나타내고 있다. 쉘 요소에 비해, 솔리드 요소의 결과값이 전체적으로 9%에서 13% 큰 하중 값을 나타내며, 이러한 주요 원인은 최대응력 위치를 쉘에서는 중립축에서 솔리드요소는 두께방향으로 추출하였기 때문이다.
A comparative results of the shell and solid element with mesh size of 5mm under impact load
4. 결론 및 향후 연구과제
본 연구논문에서는 해양구조물에 필수적인 구성요소인 알루미늄 헬리데크의 상면을 구성하는 데크 단면의 상세 구조 강도 검토에 대해서, 여러 가지 매개변수의 영향(모델링 방법, 요소 크기, 해석종류)에 대해서, 유한요소시리즈해석을 통한 결과 분석을 통하여 이와 관련한 구조 엔지니어링 시 참조가 될 수 있는 기본적인 결과를 도출하였다. 본 연구를 통해서 얻은 결론은 다음과 같다.
- ① 요소의 크기가 작은 경우 (25mm 이내) 헬리데크 상면과 수직부재가 만나는 연결지점에서 항복 응력 요소가 넓게 분포하며, 요소의 크기가 25mm 이상에서부터는 항복 응력 부위는 경계조건 근방에서 국부적으로 발생한다.
- ② 선형 고유치 좌굴해석을 통하여 구해진 임계 좌굴하중 값은 초기항복 하중과 최종강도 하중 값보다 크게 도출되고 있다. 이는 생산 시 발생할 수 있는 초기 처짐 0.5mm에 대한 영향 및 비선형성을 고려하지 않았기 때문이다.
- ③ 초기하중이 발생하는 데크 상면과 수직부재의 만나는 위치에서 실제 라운드 형상을 반영하면, 초기항복 하중은 12%, 최종강도 하중은 13% 높게 평가하는 경향이 나타난다. 이 위치가 주요 취약부위이므로, 구조 강도 평가 시 실제의 형상을 고려한 합리적인 모델링이 필요로 한다.
- ④ 실제의 붕괴거동 및 응력 패턴은 솔리드 요소를 사용한 경우가 조금 더 합리적이며, 특히 구조붕괴 위치 및 패턴에 대한 분석이 필요할 경우에는 솔리드 요소를 적용한 검토가 필요하다.
향후 연구과제로서는 다양한 설계 조건(헬리콥터 착륙 위치, 하중 크기 변화, 연속모델에서의 강도검증 등)을 종합적으로 반영할 수 있는 설계 시스템 개발이며 이러한 연구를 위하여 본 연구에서는 기초적인 검토 및 절차에 대해서 검토하였다.
Acknowledgments
본 연구는 산업통상자원부 해양융복합소재산업화사업(No. 10053841) ‘조선해양 규정을 만족하는 섬유기반 복합소재의 그린십 상부구조 표준화 부품 개발’ 과제의 지원을 받아 수행된 과제이며, 지원에 대해 감사드립니다.
Author Contributions
Conceptualization, H. Y. Jang, K. C. Seo and J. S. Park; Methodology, H. Y. Jang and K. C. Seo, Formal Analysis, J. S. Park; Validation, K. C. Seo and J. S. Park; Writing-Original Draft Preparation, H. Y. Jang; Writing-Review & Editing, J. S. Park; Project Administration, H. Y. Jang; Funding Acquisition, H. Y. Jang;
References
- The Export-Import Bank of Korea, “Prediction of economic and industry for domestic & global in 2019,” 2018 Annual Report, vol. 12, pp. 2-4, 2018.
- J. S. Park and J. K. Seo, “Deformation-based design method of aluminium helideck for eurocode 9,” Journal of Applied Mechanical Engineering, vol. 6, no. 2, pp. 1-6, 2017.
- R. Chacon, E. Mirambell, and I. Arrayago, “Flexural response of multi-stiffened aluminium beams in dock platforms,” Marine Structures, vol. 56, pp. 250-257, 2017.
- J. H. Chun, Safety Assessment of Offshore Plant Helideck Subjected to Helicopter Collision Impact, M. S. Thesis, Department of Naval Architecture and Ocean Engineering, Pusan National University, Korea, 2014 (in Korean).
- B. M. Kim, J. J. Leem, and S. H. Ha, “Safety evaluation of a cantilever-type helideck under nonlinear buckling,” Journal of the Korean Society of Marine Engineering, vol. 42, no. 3, pp. 203-209, 2018 (in Korean).
- Helicopter Decks, OS-E401, Det Norske Veritas (DNV), 2001.
- Standards for Offshore Helicopter Landing Areas, CAP-437, Civil Aviation Authority (CAA), 2013.
- J. S. Jo, J. H. Choi, and J. H. Kim, “The strength analysis of tie-down for offshore helideck,” The Korean Society of Mechanical Engineers Conference, pp. 3438-3441, 2015 (in Korean).
- Y. Q. Wang, H. X. Yuan, T. Chang, X. X. Du, and M. Yu, “Compressive buckling strength of extruded aluminium alloy I-section columns with fixed-pinned end conditions,” Thin-Walled Structures, vol. 119, pp. 396-403, 2017.
- Z. X. Wang, Y. Q. Wang, S. J. Jeong, and Y. W. Ouyang, “Experimental investigation and parametric analysis on overall buckling behavior of large-section aluminum alloy columns under axial compression,” Thin-Walled structures, vol. 122, pp. 585-596, 2018.
- MatWeb Material Property Data, http://www.matweb.com, , Accessed January 7, 2019.
- ANSYS Multiphysics Ver. 18 : User’s Manual, Introduction of nonlinear analysis and it’s application of plate buckling and ultimate strength, vol. 3, pp. 85-110, 2016.