[ Original Paper ]

Journal of the Korean Society of Marine Engineering - Vol. 43, No. 7, pp.545-551

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date 30 Sep 2019

Received 16 Jul 2019 Revised 24 Sep 2019 Accepted 26 Sep 2019

DOI: https://doi.org/10.5916/jkosme.2019.43.7.545

시간 지연이 있는 2차 시스템에 대한 안정화 제어기 설계

배상욱¹ ; 양정현² ; 권재성³ ; 최성웅⁴ ; 김범수^†

Design of stabilizing controller for second-order time-delay system

Sang-Wook Bae¹ ; Jeonghyeon Yang² ; Jaesung Kwon³ ; Sungwoong Choi⁴ ; Beomsoo Kim^†

1Professor, Department of Application Robotics, Kyungil University, Tel: 053-600-4058 swbae@kiu.ac.kr
2Associate Professor, Department of Mechanical System Engineering, Gyeongsang National University, Tel: 055-772-9107 wjdgusl81@gnu.ac.kr
3Associate Professor, Department of Mechanical System Engineering, Gyeongsang National University, Tel: 055-772-9102 jkwon@gnu.ac.kr
4Associate Professor, Department of Mechanical System Engineering, Gyeongsang National University, Tel: 055-772-9103 younhulje@gnu.ac.kr

Correspondence to: ^†Associate Professor, Department of Mechanical System Engineering, Gyeongsang National University, 38, Cheondaegukchi-gil, Gyeongsangnam-do, 53064, Korea, E-mail: kimbs@gnu.ac.kr, Tel: 055-772-9101

Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

본 연구에서는 Lambert W 함수를 이용해서 시간 지연이 있는 2차 시스템에 대한 안정화 조건을 제시한다. 2차 시간지연 시스템의 실근 존재 여부를 두 개의 함수를 정의한 후 이 함수들의 그래프 특성을 이용해서 진동 및 비진동 조건을 구한다. 비 진동 조건으로부터 안정화 조건을 구한다. 그리고 진동하거나 불안정한 시스템을 상태 궤환제어를 통해서 점근적으로 안정화 시키는 제어 이득을 쉽게 구할 수 있음을 보인다. 마지막으로, 수치 예를 통해서 제시된 방법의 효과와 장점을 보인다.

Abstract

In this paper, we propose the stability conditions for a second-order time-delay system using the Lambert W function. Oscillation and non-oscillation criteria for a second-order delay differential equation were obtained by defining two functions and using their graphical properties. The stability conditions were derived based on the non-oscillation criteria. Oscillation or unstable systems can be asymptotically stabilized by static state feedback, in which the feedback gain is easily determined. Finally, the effectiveness and merits of the proposed approach were demonstrated through numerical examples.

Keywords:

Time-delay system, Stability, Lambert W function, State feedback control

키워드:

시간지연 시스템, 안정도, 램버트 W 함수, 상태 궤환제어

1. 서 론

공학, 경제학, 생물학 등 많은 분야에서 시스템이 시간 지연을 갖는 미분방정식으로 표현된다[1]-[3]. 시간 지연성분이 지연 미분 방정식(DDE, Delay Differential Equation)으로 모델링될 때 초월 특성(transcendental characteristics)에 의해 DDE는 무수히 많은 고유치를 가질 뿐만 아니라 시간 지연이 안정도에 미치는 영향을 고려해야 하며 이는 시스템 해석을 어렵게 한다. 따라서 시간 지연이 있는 시스템의 안정도 해석 문제는 중요한 연구 주제로서 많은 연구가 수 십년간 지속적으로 진행되어 왔다[4]-[6]. 시간 지연 시스템에 대한 안정도 해석은 Lyapunov-Krasovskii 범함수를 이용하는 방법과 주파수 영역 기법이 주로 사용된다. 전자는 주로 선형 행렬 부등식의 해를 찾는 문제로 귀결되고, 후자는 시스템의 고유값을 구하는 스펙트럼 방법으로서 상대적으로 계산량이 적고 해를 해석적으로 구할 수도 있다.

DDE가 실근을 갖지 못하면 진동(Oscillation) 하고, 하나 이상의 실근을 가지면 비진동(Nonoscillation)이다[7]. 따라서 진동과 비진동 조건은 DDE 의 특성을 파악하는데 중요한 요소로 볼 수 있다. 일반적으로 DDE의 해를 해석적으로 구하기는 매우 어려워서 진동과 비진동할 충분 또는 필요충분 조건을 찾는 연구가 활발히 진행되어 왔다[8]. 단일 시간지연을 갖는 특수한 형태의 DDE는 Lambert W 함수로 이용하여 해를 해석적으로 구할 수 있지만[9], 보다 복잡한 경우에는 Newton Raphson 방법이나 Halley 반복법 등 수치 방법으로 해를 구한다[10].

시간 지연 시스템이 가질 수 있는 실근 개수에 관해서 [11]에서 단일 시간 지연 항을 포함하고 있는 2차 시간 지연 시스템이 해당 특성방정식의 계수가 특정 조건과 특정 시간지연을 만족하는 한정된 경우에 대해서 실근이 존재하고 그 실근이 최우측 근임을 주파수영역에서 Polya-Szego의 경계조건을 이용하여 구할 수 있음을 보였다. 2차 시간지연시스템의 연구 결과를 보면, [12]에서는 시간지연 시스템의 안정도, 가제어 문제를 행렬 Lambert W 함수를 이용하여 해를 수치 반복적으로 구하는 방법을 제시하였다. 2차 시스템으로 표현된 밀링 머신에 시간 지연이 포함된 상태 궤환 문제를 [13]에서 단일 제어 이득만 갖는 능동 댐핑(active damping) 제어 기법을 통해 채터(chatter)를 저감시키는 방법을 제시하였다. [14]에서는 2차 시스템으로 표현된 밀링 머신에 시간 지연이 포함된 상태 궤환 문제를 단일 제어 이득만 갖는 지연 댐핑 Mathieu 방정식을 이용해서 안정도 영역을 구하였다. 반잠수식 시추선(Semisubmersible system Rig)에서 2차 시간 지연 시스템으로 모델링된 롤 진동(Roll vibration) 문제를 준이산화(Semi-discretization) 방법을 이용하여 안정도를 구하였다[15].

본 연구에서는 시간 지연이 있는 2 차 시스템의 특성을 분석하고 시스템을 안정화시키는 제어기를 설계하기 위해 두 함수의 차가 원래 시스템의 특성방정식과 같도록 함수 2 개를 정의한다. 정의된 함수가 블록성을 가질 조건을 Lambert W 함수를 이용해서 구하며, 두 함수의 교차 여부 조건을 구함으로써 시간 지연 2 차 시스템의 진동, 비진동 조건을 구한다. 그리고 시스템이 비진동할 때 근의 위치가 복소평면의 좌방면과 우방면에 위치할 조건을 제시한다. 정의된 두 함수의 교차점이 원래 특성방정식의 해와 일치하므로, 교차점을 Lambert W 함수를 이용해서 조절함으로써 진동 또는 불안정한 시스템을 안정화 할 수 있는 상태 궤환 제어기를 설계할 수 있음을 보인다. 또한 제어기 이득을 해석적으로 구할 수 있는 방법을 제시한다. 마지막으로 수치 예를 통해서 제안된 방법의 효용성을 보인다.

2. 시간지연이 있는 2차 시스템

2.1 시간 지연이 있는 2차 시스템의 특성방정식

이 절에서는 다음과 같은 시간 지연을 갖는 2차 시스템을 고려한다.

x ¨ t + a x ˙ t + b x t + c x t - τ = 0

(1)

여기서 a,b,c∈R , τ∈R⁺이다. 여기서 R은 실수, R⁺는 양의 실수를 뜻한다. 식 (1)의 특성방정식은 시간지연 τ가 지수 항으로 나타나 다음과 같은 준 다항식(quasi-polynomial)으로 표현된다.

p s = s 2 + a s + b + c e - τ s = 0

(2)

여기서 s=α+jβ, α,β∈R이다. 준 다항식 (2)의 형태는 간단하지만, 식에 포함된 초월 항이 복소수 공간에서 무한개의 근을 갖게 한다.

다음과 같이 함수 f(s),g(s)를 정의한다.

f s = s 2 + a s + c e - τ s

(3)

g s = - b

(4)

그러면 두 함수의 차는 특성방정식 (2)와 같다.

p s = f s - g s

(5)

따라서 두 함수 f(s),g(s)의 교점(intersection points)은 특성방정식 (2)의 해와 동일하다.

Lambert W 함수 W(z) 는 ye^y=z, z∈C 의 역함수로 정의되며 초월함수 특성에 의해 다음과 같이 무수히 많은 가지(branch)를 갖는다[16].

W k z ∈ y ∈ C z = y e y, k ∈ Z

(6)

여기서 k=0 인 W₀(z)를 주가지(principal branch) 라 하고, 주가지는 스칼라 지연 미분 방정식에서 해의 안정성을 판단하는 주요 지표가 된다.

보조정리 1. 식 (3)에서 c>0이면 f(s)는 순볼록(strictly convex) 함수이다.

증명: 먼저 a>0일 경우를 고려하자. 식 (3)에서 a>0 이고 c>0 이면 f(∞)=∞이다. 그리고 $lim s → - ∞ ⁡ f ˙ s = - ∞$ 이므로 f(-∞)=∞이다. f(s)의 극값은 일계 도함수 식 (7)을 0 으로 놓고 다음과 같이 구한다.

f ˙ s = 2 s + a - c τ e - τ s

(7)

f ˙ s = 0 ⇔ 2 s + a e τ s = c τ

(8)

식 (8)의 양변에 $τ 2 e a τ / 2$ 를 곱하면 다음과 같은 형태로 나타낼 수 있다.

τ s + τ a 2 e τ s + τ a 2 = c τ 2 2 e a τ / 2

(9)

Lambert W 함수를 이용하면 식 (9)의 해는 다음과 같이 구해진다. 본 논문에서는 이 해를 s_m이라 간략히 표기한다.

s m = 1 τ W c τ 2 2 e τ a 2 - a 2

(10)

식 (10)으로 구해진 s_m 근방에서 s_δ=s_m+δ, δ∈R, 와 같이 정의한 후 이 변수를 일계 도함수 식 (7)에 대입하면 다음과 같다.

f ˙ s m + δ = 2 s m + 2 δ + a - τ c e - τ s m - τ δ

(11)

식 (11)에서 식 (7)을 빼면

f ˙ s m + δ - f ˙ s m = 2 δ - τ c e - τ s m e - τ δ - 1

(12)

와 같이 두 지점 사이의 기울기의 차를 구할 수 있다. 여기서 δ>0이면, 즉 극값 s_m의 오른쪽에서의 기울기는 양의 값을 갖고, δ<0이면 s_m의 왼쪽에서는 기울기가 음의 값이다. 따라서 s_m이 전역 최소값 (global minimum) 이고 s_m을 기준으로 f(s)는 양 방향에서 순증가(strictly increasing)한다. 그리고 f(s)의 2계 도함수는 $f ¨ s = 2 + τ 2 c e - τ s$ 이므로 모든 s에 대해서 양의 값을 가지므로 f(s)는 a>0,c>0일 때 순볼록 함수이다. 다음은 a<0일 경우를 고려한다. 식 (7)에서 $f ˙ ∞ = ∞$ 이므로 f(∞)=∞이다. 따라서 f(s)는 a<0,c>0 일 때 순볼록 함수이다.

식 (3)에서 $f ˙ 0 = a - c τ$ 이므로 s=0에서의 f(s) 기울기는 파라미터 a,c,τ에 의해서 결정된다. a>0,c>0 일 때 s=0에서 기울기가 양이면 보조정리 1에 의해서 f(s)는 순블록 함수이므로, 식 (10)으로 표현된 f(s)의 극값은 음(negative)이며, 기울기가 음이면 극값은 양(positive)이다.

정리 1. c>0일 때 f(s_m)>-b 이면 특성방정식 (2)의 모든 해는 진동(oscialltion)한다.

증명: 보조정리 1에 의해서 c>0이면 f(s)는 순블록 함수이고 s=s_m에서 전역 최소값이 존재하므로 f(s_m)>-b 이면 식 (3)은 식 (4) 위에만 존재하여 두 함수는 교차하지 않아 특성방정식 (2)는 실근을 갖지 않는다.

정리 2. c>0일 때 f(s_m)≤-b 이면 특성방정식 (2)는 최대 3개의 실근을 갖는다.

증명: f(s_m)=-b이면 식 (3)의 최소값이 식 (4)와 접하므로 실근이 존재한다. Polya-Szego 정리[11][17]에 따르면 특성방정식 (2)의 최대 실근 개수는 3을 넘지 않으므로 두 함수가 접할때 근의 대수 중복도 (algebraic multiplicity)는 3 까지 가능하다. f(s_m)<-b이면 식 (3)의 최소값이 식 (4) 아래에 위치하게 되고, 보조정리 1에 따라서 식 (3)이 순블록 함수이므로 식 (3)과 식 (4)는 두 점에서 교차하여 특성방정식은 2개의 실근을 갖는다.

정리 3. 다음 조건을 만족하면 특성방정식 (2)는 음의 실근 2개를 갖는다.

(i) c>0,a>cτ
(ii) f(s_m)<-b
(iii) b+c>0

증명: 정리 2에 따르면 c>0이고 f(s_m)<-b 일 때 특성방정식 (2)는 실근 2 개를 갖는다. 조건 (i)의 a>cτ 이면 식 (3) 은 s=0 에서 기울기가 양수이므로 식 (3)의 최소값은 s=0인 축의 왼쪽에 위치한다. b+c>0 일 때, 즉, -b<c 이면 c값 아래에서만 두 함수 식 (3)과 식 (4)의 교점이 존재하고, f(s)가 순블록 함수이므로 두 교점은 음수이다.

정리 4. 다음 조건을 만족하면 특성방정식 (2)는 양의 실근 2개를 갖는다.

(i) c>0,a<cτ
(ii) f(s_m)<-b
(iii) b+c>0

증명: 조건 (i)에서 a<cτ이면 식 (3)은 s=0 에서 기울기가 음수이므로 식 (3)의 최소값은 s=0인 축의 오른쪽에 위치한다. 나머지 과정은 정리 3과 동일하다.

정리 5. 다음 조건을 만족하면 특성방정식 (2)는 음의 근 s_m을 갖는다.

(i) c>0,a>cτ
(ii) f(s_m)=-b
(iii) b+c>0

증명: f(s_m)=-b 이면 s=s_m에서 f(s)와 g(s)가 접하므로 특성방정식은 s=s_m인 근을 갖으며, 이 근은 Polya-Szego 경계조건에 따라서 최대 3의 대수 중복도를 갖는다. 나머지는 정리 3의 증명 과정과 동일하다.

2.2 시간 지연이 있는 2차 시스템에 대한 안정화 제어기 설계

다음과 같이 제어입력이 있는 시간지연 2차 시스템을 고려해 보자.

x ¨ t + a x ˙ t + b x t + c x t - τ = u t

(13)

여기서 a,b∈R, c∈R⁺, τ∈R⁺이고 u(t)는 제어입력이다.

시스템 (13)을 점근적으로 안정화시킬 제어 입력을 다음과 같이 상태 궤환으로 구성한다.

u t = K x t

(14)

제어 입력 (14)를 식 (13)에 대입한 후 특성방정식을 구하면 다음과 같다.

p 1 s = s 2 + a s + b - K + c e - τ s

(15)

식 (15)를 2.1 절에서와 같이 함수 두 개 f₁(s),g₁(s)를 다음과 정의한다.

f 1 s = s 2 + a s + c e - τ s

(16)

g 1 s = K - b

(17)

특성방정식의 근이 복소평면 좌측에만 존재해야 전체 시스템이 안정하므로, 정리 3과 위의 두 함수를 이용하여 이득 K를 다음과 같이 구한다.

step 1. c>0,a-cτ>0 이 만족되면, 식 (10)으로 부터 s_m을 구한다.
step 2. step 1에서 구한 s_m으로 식 (16)에 정의된 함수 값 $f 1 s m = s m 2 + a s m + c e - τ s m$ 을 구하고, 정리 3-(ii), (iii) 으로부터 부등식 f₁(s_m)<K-b<c 을 만족시키는 K을 선정한다.

위의 방법을 다음과 같이 정리할 수 있다.

정리 6. 시간지연 시스템 (13)에서 c>0,a>cτ 이 성립하면,

f 1 s m + b < K < c + b

(18)

를 만족하는 K가 존재해서 시스템을 점근적으로 안정화 시키는 음의 실근 두 개를 갖게 한다.

증명: 보조정리 1과 정리 3-(i)에 의해서 c>0,a>cτ 이면 s_m<0 이고, 부등식 식 (18)은 정리 3-(ii),(iii) 을 만족하므로 식 (15)는 음의 실근 2개를 가지며, 최우측근은 (s_m,0)사이에 속하고 두 번째 우측근은 (2s_m,s_m) 구간 내에 위치한다. 그리고 정리 3-(ii), (iii)에 의해서 부등식 식 (18)에서 상한 c+b 는 하한 f₁(s_m)+b 보다 항상 크므로 K는 항상 존재한다

참고 1. 정리 6에서 K를 부등식 식 (18) 구간의 중간 값, 즉 K=(f₁(s_m)+c+2b)/2 로 해석적으로 선정할 수 있다.

정리 7. 시간지연 시스템 (13)에서 c>0,a>cτ 이 성립하면, K=f(s_m)+b 은 시스템 (13)을 점근적으로 안정화 시킨다.

증명: 보조정리 1과 정리 5에 따라서, 식 (15)에서 b-K=-f₁(s_m)이면 시간지연 시스템 (13)은 s=s_m<0에서 실근을 갖으며 이 실근은 시스템을 점근적으로 안정화 시킨다.

참고 2. 정리 7에서 극값과 K는 시스템 파라미터에 따라 정해진다. 주어진 파라미터 값을 변경하여 원하는 극배치를 하기 위해서는 식 (10)에서 Lambert W 함수의 역함수를 이용해서 구해야 하나 이는 쉽지 않다.

정리 8. 시간 지연이 포함된 제어 입력이 있는 식 (19)와 같은 2차 시스템을 고려해보자.

x ¨ t + a x ˙ t + b x t = u t

(19)

여기서 a∈R⁺,b∈R 이다. 조건(i), (ii)를 만족하는 제어 입력 u(t)=K₁x(t)+K₂x(t-τ)은 시스템 (19)를 점근적으로 안정시킨다.

(i) -α/τ<K₂<0
(ii) f₂(s_n)<K₁-b<-K_d

여기서 τ>0, s_n=1/τW(-K₂τ/2e^ατ/2)-α/2이고 $f 2 s n = s n 2 + a s n + K 2 e - τ s n$ 이다.

증명: 정리 5에 따라서, 식 (19)가 음의 실근을 갖기 위해서는 K₂<0이고 K₂>-a/τ를 만족해야 한다. 또한 a>0,τ>0이므로 조건 (i)의 부등식에서 상한 값은 하한값 보다 크므로 부등식을 만족시키는 K₂는 항상 존재한다. 조건 (i)에서 구해진 K₂를 이용해서 정리 5의 (ii) 와 (iii)을 이용하면 조건 (ii) 가 쉽게 구해진다. 따라서 조건 (i), (ii)를 만족하면 시스템 (19)는 음의 실근 2 개를 가지며, 시스템은 점근적으로 안정하다.

참고 3. 정리 8에서 K₂와 K₁는 각각 구간의 중간값 K₂=-a/(2τ), K₁=(f₂(s_n)-K₂+2b)/2로 선정할 수 있다.

3. 수치 예

예 1. 다음과 같은 시간 지연 시스템을 고려하자.

x ¨ t 10.9 x ˙ t - 14 x t + 10.5 x t - τ = u t

(20)

식 (20)에서 u(t)=0 일 때의 특성방정식은 다음과 같이 구해진다

s 2 + 10.9 s - 14 + 10.5 e - τ s = 0

(21)

식 (21)에서 시간 지연이 근의 위치에 미치는 영향을 보기 위해 τ가 0.3, 0.6, 0.8 일 때의 근을 수치 해석 방법인 QPmR (Quasi-polynomial root-finder, [18]) 로 구해보면 Table 1과 같다.

Table 1

Roots of the characteristic equation (21) for τ = 0.3,τ = 0.6,τ = 0.8

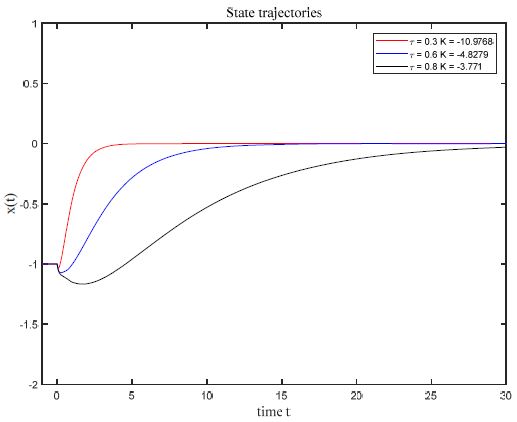
각 시간지연에 대해서 특성 방정식은 복소평면 우방면에 근이 있는 불안정한 시스템이다. 정리 6을 이용해서 상태 궤환 제어 u(t)=Kx(t)의 제어 이득을 구하면 τ가 0.3, 0.6, 0.8일 때 K 를 참고 1의 방법에 의해서 -10.9768, -4.82793, -3.77098 로 선정했으며, 각 경우에서의 구해진 근은 Table 2와 같다.

Table 2

Roots of the time delayed system with state feedback

Table 2에서 볼 수 있듯이 제어 입력을 시스템에 인가하였을 때 시스템의 최우측 근은 각각 –1.3014, -0.3887, -0.1476 이고 두 번째 우측 근은 –3.2622, -0.9757, -0.377 이며 각 경우에서 식 (10)으로 주어진 s_m은 -2.30509, -0.688574, -0.263676 로 구해졌다. 따라서 정리 6 에서와 같이 최우측 근과 두 번째 우측 근이 각각 구간 (s_m,0)와 (2s_m,s_m)사이에 위치함을 보여 준다.

Figure 1은 초기 함수 x(t)=-1,-τ<t<0 에 대해서 제어 입력을 인가했을 때 상태 궤적으로서, 빨간 실선, 파란실선, 검은 실선 궤적은 각각 τ가 0.3, 0.6, 0.8 에 해당된다. 시간 지연이 클수록 수렴 시간이 큼을 알 수 있다.

Figure 1

The state trajectories of the time-delay system (20) with a state feedback controller.

예 2. 다음과 같은 시간 지연 시스템을 고려하자.

x ¨ t + 5.9 x ˙ t + 4 x t + 2.5 x t - 0.7 = u (t)

(22)

식 (22) 에서 제어 입력이 없는 경우의 특성방정식 근을 QPmR로 구했을 때, 최우측 근 4개는 -1.2030±1.3376i, -4.9130±8.3551i 이다. 정리 7을 이용해서 상태 궤환 제어기를 설계할 때 식 (10)으로 주어진 s_m은 -1.08281로 구해지고, 제어 이득은 K=4.11873 와 같이 해석적으로 구할 수 있다. 이 제어 입력을 인가했을 때 시간 지연 시스템 (22)의 근을 QPmR로 구하면, 최우측 2개 근은 –1.08281 로 중복된 값을 갖는다. Figure 2 (a) 와 Figure 2 (b)에 시스템 (22)에서 제어입력이 없을 때와 위에서 설계한 제어입력을 인가했을 때 스펙트럼 분포를 나타내었다.

Figure 2

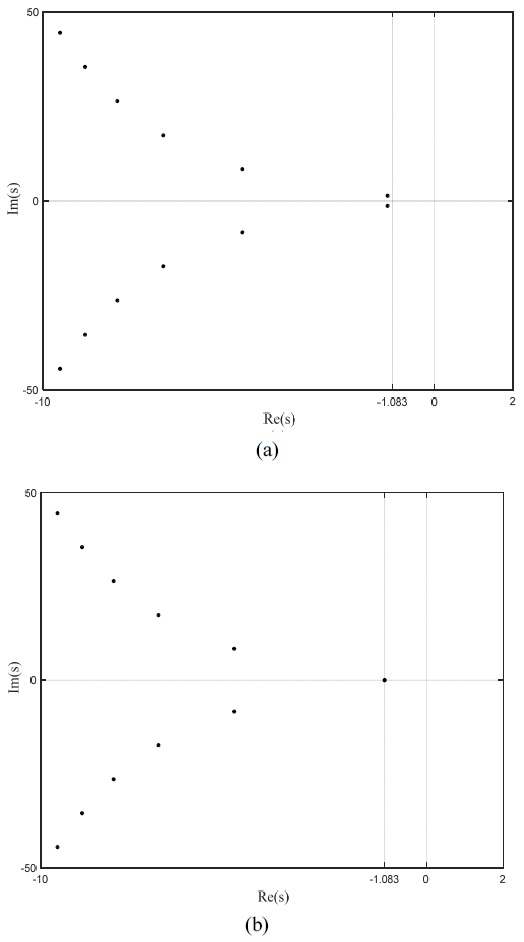
The spectrum distribution of time-delay system (22). (a) without state feedback, (b) with a state feedback controller. The designed controller makes the system has double real roots at -1.08281.

예 3. 다음과 같은 2차 시스템에서 입력에 시간 지연이 있는 경우를 고려하자.

x ¨ t + 5.2 x ˙ t + 3.1 x t + K 1 x t + K 2 x t - τ

(23)

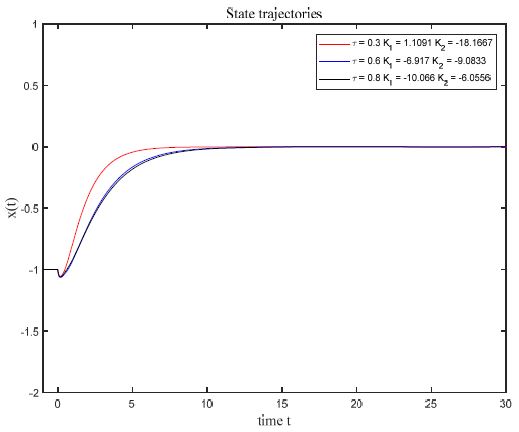
이 시스템에서 제어 입력이 없을 때의 특성방정식 근은 -2.6±1.6882i 로 구해진다. 식 (23)과 같이 시스템에 시간지연이 궤환될 때 계수쌍 (K₁,K₂)는 정리 8에 제시된 방법으로 구해 보면 시간 지연이 각각 0.3, 0.6, 0.8 일 때 (1.1091, -18.1667), (-6.917, -9.0833), (-10.0666, -6.0556)으로 구해지고 그때 시스템은 각각 (-0.7614, -1.9327), (-0.4915, -1.2222), (-0.4644, -1.1360) 와 같이 음의 실근을 갖는다.

시간 지연이 클수록 최우측 실근이 0 에 가까워지는 것을 볼 수 있다. Figure 3은 초기 함수 x(t)=-1,-τ<t<0 에 대해서 시간 지연이 있는 제어입력을 인가했을 때, 빨간 실선, 파란실선, 검은 실선은 각각 τ가 0.3, 0.6, 0.8 일 때의 상태 궤적이다.

Figure 3

The state trajectories of the second order system (23) with a time-delay feedback controller

4. 결 론

본 논문에서는 시간 지연이 있는 2 차 시스템의 진동, 비 진동 조건 유도하였다. 시스템이 비진동할 때 실근의 위치를 알 수 있는 조건을 Lambert W 함수를 이용해서 명시적으로 제시함으로써 진동 또는 불안정한 시스템의 실근이 복소평면 좌방면에 오도록 상태 궤환 제어기를 해석적으로 설계할 수 있음을 보였다. 그리고 수치 예를 통해 제안된 방법의 타당성을 보였다. 추후 시간지연을 갖는 물리적 시스템에 제안된 방법을 적용한 실험을 통해 본 연구의 효용성 입증에 관한 연구가 필요하다.

Acknowledgments

이 연구는 2019년도 경상대학교 연구년제 연구교수 연구지원비에 의하여 수행되었음.

Author Contributions

Conceptualization, S. Bae and B. Kim; Methodology, B. Kim; Software, J. Kwon; Validation, S. Bae and B. Kim; Formal Analysis, S. Kim; Investigation, J. Yang; Resources, S. Choi; Data Curation, B. Kim; Writing-Original Draft Preparation, B. Kim; Writing-Review & Editing, J. Yang; Visualization, J. Kwon; Supervision, B. Kim; Project Administration, B. Kim; Funding Acquisition, B. Kim;

References

T. Erneux, Applied Delay Differential Equations, Springer Science & Business Media.T, 2009.
C. Jin, K. Gu, S. I. Niculescu, and I. Boussaada, “Stability analysis of systems with delay-dependent coefficients: an overview,” IEEE Access, vol. 6, pp. 27392-27407, 2018.
K. Gu and S. I. Niculescu, “Survey on recent results in the stability and control of time-delay systems,” Journal of dynamic systems, measurement, and control, vol. 125, no. 2, pp. 158-165, 2003.
R. Sipahi, S. I. Niculescu, C. T. Abdallah, W. Michiels, and K. Gu, “Stability and stabilization of systems with time delay,” IEEE Control Systems Magazine, vol. 31, no. 1, pp. 38-65, 2011.
B. S. Kim and J. S. Kwon, “Stability analysis for singularly perturbed time delayed system,” Journal of the Korean Society of Marine Engineering, vol. 42, no. 7 pp. 566-571, 2018 (in Korean).
B. S. Kim, “Stabilizing controller design for time-delay singularly perturbed systems by H∞ Norm and Lambert W function,” The Transactions of the Korean Institute of Electrical Engineers, vol. 62, pp. 1144-1150, 2014 (in Korean).
A. F. Yenicerioglu, “The behavior of solutions of second order delay differential equations,” Journal of Mathematical Analysis and Applications, vol. 332, no. 2, pp. 1278-1290, 2007.
G. Ladas and Y. G. Sficas, “Oscillations of neutral delay differential equations,” Canadian Mathematical Bulletin, vol. 29, no. 4, pp. 438-445, 1986.
S. A. He and I. Fong, “Stability and performance of first-order linear time-delay feedback systems: an eigenvalue approach,” Journal of Control Science and Engineering, vol. 27. 2011.
Z. H. Wang, “Numerical stability test of neutral delay differential equations,” Mathematical Problems in Engineering, vol. 2008, 2008.
I. Boussaada, S. Tliba, S. I. Niculescu, H. U. Unal, and T. Vyhlidal, “Further remarks on the effect of multiple spectral values on the dynamics of time-delay systems,” Application to the control of a mechanical system. Linear Algebra and its Applications, vol. 542, no. 4, pp. 589-604, 2018.
S. Yi, P. W. Nelson, and A. G. Ulsoy, “Controllability and observability of systems of linear delay differential equations via the matrix Lambert W function,” IEEE Transactions on Automatic Control, vol. 53, no. 3, pp. 854-860, 2008.
A. B. Ganguli, A. Deraemaeker, and A. Preumont, “Regenerative chatter reduction by active damping control,” Journal of sound and vibration, vol. 300, no. 3, pp. 847-862, 2007.
F. A. Khasawneh and B. P. Mann, “A spectral element approach for the stability analysis of time-periodic delay equations with multiple delays,” Communications in Nonlinear Science and Numerical Simulation, vol. 18, no. 8, pp. 2129-2141, 2013.
R. K. Mitra, A. K. Banik, T. K. Datta, and S. Chatterjee, “Nonlinear roll oscillation of semisubmersible system and its control,” International Journal of Non-Linear Mechanics, vol. 107, no. 12, pp. 42-55, 2018.
R. M. Corless, G. H. Gonnet, D. E. Hare, D. J. Jeffrey, and D. E. Knuth, “On the Lambert W function,” Advances in Computational mathematics, vol. 5, no. 1, pp. 329-359, 1996.
G. Polya and G. Szego, Problems and Theorems in Analysis, vol. I: Series, Integral Calculus, Theory of Functions, Springer-Verlag, New York, Heidelberg, and Berlin, 1972.
T. Vyhlidal and P. Zitek, “QPmR-Quasi-polynomial root-finder: Algorithm update and examples,” Delay Systems. Advances in Delays and Dynamics, vol 1. T. Vyhlídal, Ed. Springer, Cham, pp. 299-312, 2014.