[ Original Paper ]

Journal of the Korean Society of Marine Engineering - Vol. 43, No. 7, pp.535-544

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date 30 Sep 2019

Received 19 Jun 2019 Revised 22 Aug 2019 Accepted 9 Sep 2019

DOI: https://doi.org/10.5916/jkosme.2019.43.7.535

외향 반경류 터빈의 예비설계에 관한 기초연구

김준성¹ ; 김유택² ; 김도엽^†

A fundamental study on the preliminary design of a radial outflow turbine

Jun-Seong Kim¹ ; You-Taek Kim² ; Do-Yeop Kim^†

1Ph.D. Candidate, Department of Convergence Study on the Ocean Science and Technology, Ocean Science and Technology School, Korea Maritime & Ocean University, Tel: 051-410-4862 kylejune@kmou.ac.kr
2Professor, Division of Marine System Engineering, Korea Maritime & Ocean University, Tel: 051-410-4258 kimyt@kmou.ac.kr

Correspondence to: ^†Assistant professor, Division of Marine System Engineering, Korea Maritime & Ocean University, 727, Taejong-ro, Yeongdo-gu, Busan 49112, South Korea, E-mail: doyeop@kmou.ac.kr, Tel: 051-410-4282

Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

최근 강화되는 배출가스 규제에 대응하여 친환경 발전 사이클이 주목받고 있다. 터빈은 발전 사이클의 효율에 있어 지대한 영향을 미치는 요소이다. 근래 발전 사이클용 외향 반경류 터빈에 관한 연구가 진행되고 있다. 외향 반경류 터빈은 축류 터빈과 내향 반경류 터빈이 가진 이점을 모두 지니고 있기 때문이다. 터빈의 예비설계에 있어 목표 효율을 분명히 할 필요가 있다. 그러나 기존의 연구들은 터빈의 예비설계에서 목표 효율이 불분명하다. 본 연구에서는 목표 효율을 입력변수로 사용하는 외향 반경류 터빈의 예비설계에 관하여 기초연구를 수행한다. 예비설계에 적합한 설계모델들을 고려하였으며, 외향 반경류 터빈의 목표 성능을 만족시키기 위한 독창적인 알고리즘을 제시하였다. 예비설계프로그램의 검증을 위하여 전산유체역학을 수행하였다. 그 결과, 외향 반경류 터빈의 설계에 있어 편향각이 중요한 변수임을 알 수 있었다. 편향각을 고려하여 노즐 깃과 로터 깃의 최적화를 수행하였다. 터빈의 최종형상에서 설계목표를 달성할 수 있었다.

Abstract

In recent years, eco-friendly power generation cycles have been attracting attention in response to enhanced emissions regulations. The turbine is a significant component in the efficiency of the power generation cycle. Currently, studies on the radial outflow turbine in power generation cycles have been carried out. This is because the radial outflow turbine has both the advantages of an axial flow turbine and a radial inflow turbine. It is necessary to clarify the target efficiency in the preliminary design of turbines. However, existing studies have unclear target efficiency in the preliminary design of turbines. In this paper, a fundamental study is conducted on the preliminary design of a radial outflow turbine that uses target efficiency as an input variable. Design models suitable for preliminary design of turbines were considered, and an original algorithm was presented to satisfy the target performance of the radial outflow turbine. Computational fluid dynamics analysis was performed for verification of preliminary design programs. The results showed that the deviation angle is an important variable in the design of the radial outflow turbine. The optimization of the nozzle and rotor blades was performed by considering the deviation angle. The design objectives were achieved in the final geometry of the turbine.

Keywords:

Radial outflow turbine, Preliminary design, Fundamental study, Computational fluid dynamics, Optimization

키워드:

외향 반경류 터빈, 예비설계, 기초연구, 전산유체역학, 최적화

1. 서 론

최근 강화되는 배출가스 규제에 대응하여 유기랭킨사이클 및 초임계 이산화탄소 사이클과 같은 친환경 발전 사이클이 주목받고 있다[1][2]. 한편, 터빈은 이러한 발전 사이클의 효율에 있어 지대한 영향을 미치는 요소이다[3]. 가장 널리 쓰이는 터빈의 종류에는 주로 축류 터빈과 내향 반경류 터빈이 있으며, 각각의 터빈은 분명한 특징이 있다. 우선, 축류 터빈은 대유량에서 유리하고, 다단으로 구성하여 높은 압력비에서도 사용가능함에 따라 고효율 및 고출력을 기대할 수 있다[4]. 내향 반경류 터빈은 소유량에 적합하며, 제작이 용이하고, 탈설계 조건에서도 성능이 우수한 장점이 있다[5]. 그러나 축류 터빈은 작동유체의 팽창에 따라 첫 단에서 마지막 단으로 갈수록 깃 높이가 상승하는 형상을 가진다[6]. 마지막 단으로 갈수록 길어지는 깃들은 허브와 팁 사이 속도삼각형의 큰 차이를 보여, 깃을 비틀어야만 하므로 제작이 어렵다[4][6]. 또한 내향 반경류 터빈은 일반적으로 1단으로만 구성되며, 높은 압력비에서 마하수에 대한 제한으로 사용에 어려움이 따르며 고출력을 요구하는 사이클에 있어 제한적이다[7].

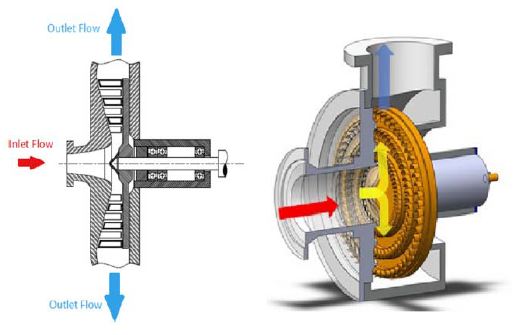
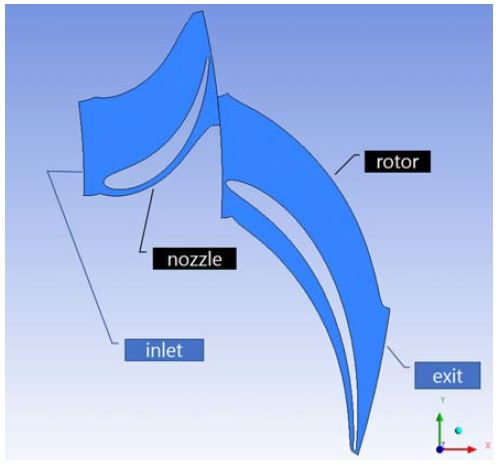
축류 터빈과 내향 반경류 터빈의 단점을 동시에 보완할 수 있는 터빈의 종류로 외향 반경류 터빈(ROT; Radial Outflow Turbine)이 있다. Figure 1은 전형적인 외향 반경류 터빈의 구조를 나타내고 있다[4][8][9]. 외향 반경류 터빈은 원심 터빈이라고도 불리며, 작동유체가 축 방향으로 유입된 후 반경 방향으로 팽창한다.

Figure 1

Conventional structure of a radial outflow turbine [4][8][9]

외향 반경류 터빈은 대표적으로 다음과 같은 장점을 가지고 있다[4][8].

(1) 팽창 과정에서 작동유체의 비체적과 함께 유동면적의 반경이 동시에 상승함에 따라, 깃 높이의 변화가 크지 않거나, 일정하도록 설계가능하다.
(2) 깃의 스팬(span)에 따라 원주속도가 일정하고, 허브와 팁 사이 속도삼각형이 일정함에 따라 깃을 비틀지 않아도 된다.
(3) 다단 구성이 용이하므로, 압력비의 제한이 없으며 고출력을 요구하는 사이클에도 사용이 가능하다.

즉, 외향 반경류 터빈은 설계와 제작에 있어 축류 터빈보다 용이하고, 다단 구성을 통하여 내향 반경류 터빈보다 높은 출력에 대응할 수 있다. 이에 따라 최근 외향 반경류 터빈에 관한 연구가 진행되고 있다. A. M. Al Jubori et al. [7]은 유기랭킨사이클용 축류 터빈 및 외향 반경류 터빈을 각각 설계하였으며, CFD를 통하여 예비설계의 결과검증 및 비교분석을 수행하였다. D. Luo et al. [8]은 초임계 이산화탄소 사이클용 외향 반경류 터빈을 예비설계한 뒤, CFD 검증 후에 출력과 효율이 만족할 때까지 깃의 형상을 최적화하였다. D. Maksiuta et al. [10]은 3MW급 폐열회수 유기랭킨사이클용 외향 반경류 터빈에 관하여 연구를 수행하였으며, 한단의 엔탈피 강하가 동일하지 않은 다단 외향 반경류 터빈을 설계하는 독창적인 예비설계기법을 제안하였다.

한편, 상기 연구들의 예비설계기법에서는 목표 효율이 불분명하다. 터빈의 효율이 열역학적 사이클에서 고려된 터빈의 효율과 상이할 시, 사이클은 터빈 효율을 고려하여 재설계되어야 한다. 그러므로 터빈의 예비설계단계에서 목표 효율을 분명히 하고, 설계된 터빈은 목표 효율을 충족할 필요가 있다[11]. 본 연구에서는 목표 효율을 입력변수로 사용하는 외향 반경류 터빈의 예비설계에 관하여 기초연구를 수행하였다. 예비설계에 적합한 설계모델들을 고려하였으며, 외향 반경류 터빈의 목표 성능을 만족시키기 위한 독창적인 알고리즘을 제시하였다. 예비설계프로그램의 검증을 위하여 3차원 유동해석(CFD)을 수행하였으며, 그 결과를 바탕으로 외향 반경류 터빈의 설계에 있어 중요변수를 밝히고 터빈의 최적화 과정을 통하여 설계목표를 충족할 수 있음을 보였다.

2. 예비설계

2.1 예비설계모델

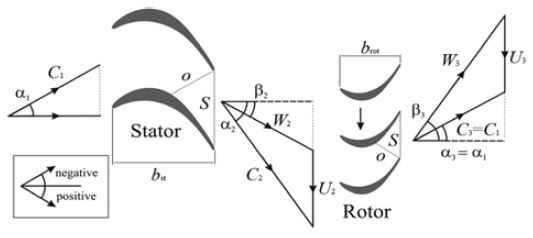
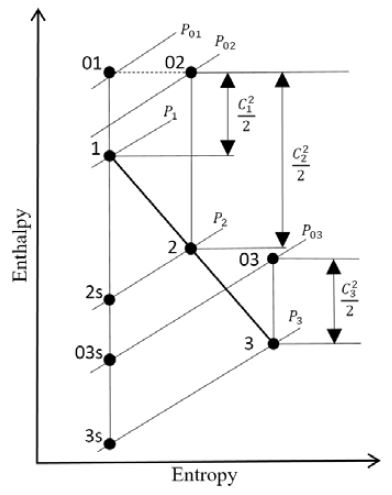
외향 반경류 터빈의 속도삼각형 및 h-s 선도는 각각 Figure 2와 Figure 3과 같다.

Figure 2

Schematic of turbine stage velocity triangle for a radial outflow turbine [7][12]

Figure 3

h-s diagram of the working fluid in a radial outflow turbine

터빈의 비출력은 오일러 방정식과 총 엔탈피 강하량으로 식 (1)과 같이 정의될 수 있다[13]. 축류 터빈과 대별되는 외향 반경류 터빈의 특징은 로터 입·출구의 원주속도가 동일하지 않다는 점이다. 즉, 외향 반경류 터빈의 경우 비출력을 저해하는 로터 출구의 접선방향 절대속도(C_3θ)를 보다 적극적으로 최소화하여야 할 필요가 있다. 식 (1)에서 질량유량은 식 (2)와 같다. 여기서, 자오선(반경) 방향의 절대속도가 일정하다면, 각 지점의 질량유량은 밀도와 유동면적만을 고려해도 된다.

W ˙ = m ˙ h 01 - h 03 = m ˙ U 2 C 2 θ - U 3 C 3 θ

(1)

m ˙ = ρ 1 C 1 m 2 π r 1 H = ρ 2 C 2 m 2 π r 2 H = ρ 3 C 3 m 2 π r 3 H

(2)

터빈의 총압-총압 효율(η_tt)과 총압-정압 효율(η_ts)는 각각 Figure 3으로부터 식 (3)과 식 (4)와 같다.

η t t = h 01 - h 03 h 01 - h 03 s

(3)

η t s = h 01 - h 03 h 01 - h 3 s

(4)

D. Maksiuta et al. [10]은 내향 반경류 터빈과 마찬가지로 외향 반경류 터빈 역시 적절한 속도비(ν)가 0.7임을 밝혔다. 속도비의 정의는 식 (5)와 같다. 여기서 로터 입구의 원주속도(U₂)와 분출속도(C₀)는 각각 식 (6)과 식 (7)과 같다. 즉, 속도비와 터빈의 열역학적 설계조건으로부터 분출속도를 정함으로써 로터 입구의 원주속도를 결정할 수 있다. 또한 로터의 회전속도(ω)를 정함으로써 로터 입구의 반경을 결정할 수 있다.

ν = U 2 / C 0

(5)

U 2 = r 2 ω

(6)

C 0 = 2 h 01 - h 03

(7)

외향 반경류 터빈일지라도 깃의 부하계수(ψ)는 터빈의 속도삼각형과 터빈의 효율에 지대한 영향을 미치는 변수이다. 즉, 외향 반경류 터빈에서도 목표 효율에 적합하도록 부하계수를 결정해야 한다. 부하계수의 정의는 식 (8)과 같으며 로터 출구의 접선방향 절대속도 성분(C_3θ)가 0이라면 식 (8)의 우변과 같이 간략하게 나타낼 수 있다.

ψ = U 2 C 2 θ - U 3 C 3 θ U 22 ≃ C 2 θ U 2

(8)

모든 터보기계의 회전체 유동에서 로탈피(I)는 보존되어야 하며, Figure 2로부터 외향 반경류 터빈의 로탈피는 식 (9)와 같이 정의된다.

I = h 2 + W 22 2 - U 22 2 = h 3 + W 32 2 - U 32 2

(9)

2.2 예비설계알고리즘

소수에 불과한 외향 반경류 터빈에 관한 연구 중에 A. M. Al Jubori et al. [7]의 연구에 주목할 필요가 있다. A. M. Al Jubori et al. [7]은 외향 반경류 터빈에 대한 명확한 설계이론의 부재를 지적하고 축류 터빈의 압력손실모델을 이용하여 외향 반경류 터빈을 설계하였다. CFD를 이용하여 설계알고리즘을 검증한 결과, 축류 터빈의 압력손실모델이 외향 반경류 터빈의 설계에도 효과적임을 보였다. 노즐의 압력손실계수(K_N, 식 (10))와 로터의 압력손실계수(K_R, 식 (11))는 각각 전압-전압 효율 및 전압-정압 효율과 식 (12) 및 식 (13)의 관계를 갖는다.

K N = P 01 - P 02 P 02 - P 2

(10)

K R = P 02 r - P 03 r P 03 r - P 3

(11)

η t t = 1 1 + K R W 32 / 2 + K N C 22 / 2 h 3 / h 2 / h 01 - h 03

(12)

η t s = 1 1 + K R W 32 / 2 + K N C 22 / 2 h 3 / h 2 + C 32 / 2 / h 01 - h 03

(13)

식 (12)와 식 (13)은 터빈의 속도삼각형과 노즐 및 로터의 압력손실계수가 효율과 밀접한 영향이 있다는 것은 의미한다. A. M. Al Jubori et al. [7]은 단지 외향 반경류 터빈이 달성할 수 있는 최대 효율에 관심을 가졌으며, 최대 효율을 달성할 수 있는 외향 반경류 터빈을 설계하기 위하여 압력손실모델을 사용하였다.

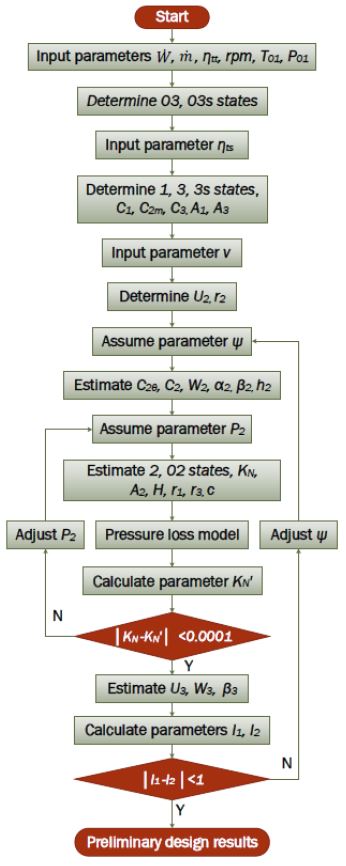
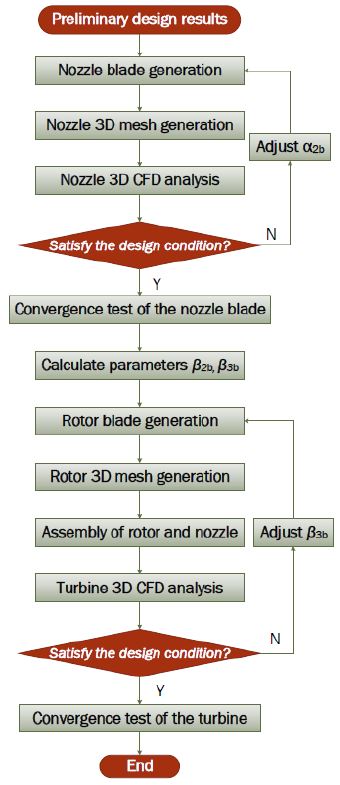
그러나, 서론에서 언급하였듯이 터빈의 효율은 열역학적 사이클의 효율과 밀접한 관계를 가진다. 만약, 열역학적 사이클에서 고려된 터빈의 효율과 실제 터빈의 효율이 크게 상이하다면 더 이상 열역학적 사이클에서 고려된 이상적인 사이클 효율을 기대할 수 없다. 그러므로 본 연구에서는 터빈의 목표 효율을 정의하고 이를 실현할 수 있는 터빈을 설계하기 위하여 압력손실모델을 이용하였다. 보다 구체적으로 속도삼각형을 결정한 이후 Figure 3의 노즐 출구에 해당하는 2 지점의 상태량은 불분명한 변수이다. 2지점의 상태량은 식 (10) ~ 식 (13)에서 보인 바와 같이 터빈의 효율에 큰 영향을 미치며, 연속방정식을 통해 터빈 깃의 높이를 결정하는 매우 중요한 변수이다. 따라서 본 연구에서는 노즐 깃의 형상과 노즐 출구의 상태량을 정확하게 예측하기 위하여 압력손실모델을 이용하였다. 본 연구에서 제시하는 예비설계알고리즘의 순서도는 Figure 4와 같다.

Figure 4

Flow chart of preliminary design for a radial outflow turbine

Figure 4의 알고리즘은 MATLAB R2016a [14]로 작성하였으며, 이 프로그램은 Nist Refprop 데이터베이스로부터 작동유체의 물성치 및 상태량을 참조할 수 있도록 개발되었다. 이 프로그램은 아래의 가정을 토대로 한다.

(1) 표준 단을 사용하며, 로터 출구의 접선방향 절대속도 성분(C_3θ)는 0이다. 그러므로 α₁=α₃=0 º다.
(2) 자오선(반경) 방향의 절대속도는 일정하다. 즉, 가정 (1)으로부터 C₃=C_3m=C_2m=C_1m=C₁의 관계가 성립한다.
(3) 노즐 깃과 로터 깃의 높이는 일정하다.
(4) 속도비(ν)는 0.7이다.
(5) 깃 출구의 편향각(deviation angle)은 무시한다.

열역학적 사이클의 설계조건들과 로터 회전속도(rpm) 그리고 목표 효율(η_ts)를 입력하고 가정 (4)의 속도비를 이용하여 노즐 출구이자 로터 입구의 반경 등을 결정한다. 부하계수(ψ)를 가정함으로써 노즐 입·출구의 속도삼각형을 기초적으로 결정한다. 이후 노즐 깃의 형상과 노즐 출구의 상태량을 결정하기 위하여, 압력손실모델을 이용하여 노즐 출구의 상태량(P₂)을 반복계산을 통하여 결정한다. 그 결과와 가정 (3)을 토대로 로터 출구의 속도삼각형이 완성되며, 로탈피 보존의 법칙에 의하여 가정된 부하계수는 반복적으로 수정된다. 상기의 반복계산을 통하여 목표 효율(η_ts)를 충족하는 속도삼각형과 외향 반경류 터빈의 노즐 및 로터의 기본적인 형상들이 결정된다.

상기 알고리즘의 핵심 요소인 압력손실모델은 아래와 같다. 깃의 압력손실에 지대한 영향을 미치는 것은 프로파일(profile) 손실과 2차(secondary) 손실이므로[15], 본 연구에서는 상기 두 가지 손실을 고려하였다. 두 손실에 의해 압력손실계수를 다시 표현하면 식 (14)와 같다. 식 (14)의 우변 첫 번째 항은 프로파일 손실을, 그리고 우변의 두 번째 항은 2차 손실을 의미한다.

K N' = f R e K P + K S e c

(14)

프로파일 손실의 K_p는 식 (15)와 같다. R. H. Aungier [16]는 Ainley and Mathieson [17]의 실험결과를 바탕으로 식 (15)의 $K P *$ 을 식 (16)과 같이 정의하였다. H. Moustapha et al. [15]에 의하면 식 (15)의 k_accel과 k_sh의 각 정의는 식 (17) ~ 식 (18)과 같다.

K P = 0.914 23 K P * K a c c e l + K s h

(15)

K P * = 0.025 + 27 - a 2' / 530, a 2' ≤ 27 ∘ 0.025 + 27 - a 2' / 3085, a 2' > 27 ∘ w h e r e, a 2' = 90 - a 2

(16)

K a c c e l = 1 - K 2 1 - K 1 w h e r e, K 1 = 1.0, M 2 ≤ 0.2 1 - 1.25 M 2 - 0.2, M 2 > 0.2 K 2 = M 1 / M 2 2

(17)

K s h = 0.75 M 1 - 0.4 1.75 P 1 P 2 1 - 1 + k - 1 2 M 12 k / (k - 1) 1 - 1 + k - 1 2 M 22 k / (k - 1)

(18)

프로파일 손실은 레이놀즈 수(Re_ref)에 의해 보정되어야 하며 식 (14)의 f_Re은 식 (19)와 같다.

f R e = R e r e f / 2 × 105 - 0.4, R e r e f ≤ 2 × 105 1.0, 2 × 105 < R e r e f ≤ 106 R e r e f / 106 - 0.2, R e r e f > 106

(19)

R. H. Aungier [16]는 노즐 깃의 압력손실이 최소가 되기 위한 피치/코드(s/c)를 식 (20)과 같이 제시하였다.

s / c = 0.46 + a 2' / 77, a 2' ≤ 30 ∘ 0.614 + a 2' / 130, a 2' > 30 ∘

(20)

한편, H. Moustapha et al. [15]이 제시한 2차 손실(K_Sec)의 정의는 식 (21)과 같다.

K S e c = 0.0334 f A S cos ⁡ α 2 cos ⁡ α 1 b C L s / c 2 cos 2 ⁡ α 2 cos 3 ⁡ α m w h e r e, f A S = 1 - 0.25 2 - h / c h / c, h / c ≤ 2 1 h / c, h / c > 2 C L s / c = 2 tan ⁡ α 1 + tan ⁡ α 2 cos ⁡ α m α m = tan - 1 ⁡ 0.5 tan ⁡ α 1 + tan ⁡ α 2

(21)

3. 예비설계프로그램의 검증

3.1 설계조건 및 예비설계 결과

본 연구에서 제시한 외향 반경류 터빈의 예비설계프로그램은 CFD를 이용하여 검증하였다. 설계조건은 D. Luo et al. [8]의 연구에서 제시된 초임계 이산화탄소용 외향 반경류 터빈의 설계조건을 참고하여 Table 1과 같이 결정하였다.

Table 1

Input parameters of preliminary design for a radial outflow turbine

Table 1의 설계조건을 토대로 예비설계프로그램이 제시하는 외향 반경류 터빈의 주요 제원은 Table 2와 같다. 그 외 반복계산을 통해 결정된 부하계수와 2지점의 정압은 각각 0.816과 10.249 MPa이며, 로터 출구의 정압(P₃)은 8.001 MPa 이다. 식 (20)에 의해 결정된 노즐의 s/c값은 0.76이며, 이는 노즐 깃의 개수가 41개여야 함을 의미한다. 노즐 깃의 개수와 로터 깃의 개수가 동일할 경우 공진 발생의 우려가 있으므로 로터 깃의 개수는 39개로 결정하였다.

3.2 CFD 해석

Table 2의 예비설계결과로부터 ANSYS-BladeGen V13.0을 이용하여 외향 반경류 터빈의 노즐과 로터의 단일 유로 형상을 각각 완성하였다(Figure 5). 완성된 형상을 토대로, ANSYS-TurboGrid V13.0을 이용하여 각 노즐과 로터에 정렬격자(hex. mesh)를 생성하였다[18].

Table 2

Results of preliminary design for the radial outflow turbine

Figure 5

One-passage geometry of the radial outflow turbine

CFD 해석프로그램으로는 ANSYS-CFX V13.0을 이용하였다. 작동유체인 이산화탄소에 관한 상태방정식은 임계조건 근방에서도 신뢰할 수 있는 Aungier-Redlich-Kwong 방정식을 사용하였으며, 식 (22)와 같이 표현할 수 있다[16].

P = R T V - b + c - a V V + b T r n w h e r e, a = 0.42747 R 2 T c 2 / P c b = 0.08664 R T c / P c n = 0.4986 + 1.1735 ω + 0.4754 ω 2 T r = T / T c

(22)

상기 식에서 상수 c는 모든 임계점 속성이 지정된 임계점에 식 (22)를 적용하여 직접 산출된다[16].

난류모델은 정밀한 경계층 내의 유동 예측을 위하여 SST(Shear Stress Transport) 모델을 사용하였다[19]. 입구 경계조건으로는 단일 유로임을 고려하여 예비설계조건인 Table 1에 나타낸 질량유량(4.45 kg/s = 182.46 kg/s ÷ 41 passages)과 전온도(773.0 K)를 부여하였다. 출구 경계조건으로는 예비설계결과인 정압(8.001 MPa)을 부여하였다. 로터 도메인의 회전속도는 예비설계조건과 동일하게 6,000 RPM이다. 노즐과 로터 도메인 사이의 인터페이스는 Frozen Rotor 모델을 설정하였다[19].

3.3 해석결과

CFD 해석결과를 예비설계조건 및 예비설계결과와 비교하면 Table 3과 같다. Table 3은 예비설계한 외향 반경류 터빈이 설계목표인 동력( $W ˙$ )과 효율(η_ts)을 만족시키지 못한다는 것을 나타내고 있다.

Table 3

Comparison between results of preliminary design and CFD

CFD 해석결과를 살펴보면 노즐 깃이 충분히 작동유체를 가속하지 못하여 C_2θ가 다소 낮을 뿐만 아니라 C_3θ는 지나치게 높다. 그 결과, 비출력이 설계조건을 만족시키지 못한 것으로 판단된다.

한편, 본 연구의 예비설계프로그램은 가정 (5)와 같이 노즐 및 로터 깃의 편향각을 무시하였다. 즉, 노즐 깃의 출구각도(α_2b)는 예비설계에서 완성된 속도삼각형의 노즐 출구 측 절대속도 각도(α₂=66.87˚)와 같고, 로터 깃의 출구 각도(β_3b)는 예비설계에서 완성된 속도삼각형의 로터 출구 측 상대속도 각도(β₃=-74.10˚)와 같다고 가정하였다. 그러나 Table 3의 결과에서 노즐 출구의 편향각은 약 6 °이며, 로터 출구의 편향각은 약 2 °로 나타났다.

소수에 불과한 외향 반경류 터빈의 연구사례에서 편향각의 중요성을 지적한 참고문헌은 전무하다. 그러나 Table 3의 결과는 외향 반경류 터빈의 설계에 있어 편향각은 반드시 고려되어야 함을 나타낸다.

4. 속도삼각형의 최적화

4.1 최적화 절차

최적화의 목표는 예비설계프로그램이 제시한 각 지점의 속도삼각형을 만족시키는 것이다. 이에 따라 본 연구에서 수립한 최적화 과정은 Figure 6과 같다.

Figure 6

Flow chart of optimization for the radial outflow turbine

로터 상류에 위치한 노즐의 입·출구 속도삼각형은 로터와는 무관하다. 즉, 노즐의 속도삼각형의 최적화 유무를 판단하기 위한 CFD에서 로터 도메인은 불필요하다. 노즐의 최적화는 오직 노즐 출구 각도만을 조정하여 수행하였다.

이후 노즐 깃의 최적화 결과를 토대로 로터 깃의 출구 각도에 해당하는 β_3b를 조정하여 로터의 최적화를 수행하였다.

4.2 노즐 속도삼각형의 최적화

노즐의 속도삼각형은 편향각을 고려하여 노즐 출구 깃의 각도 α_2b를 변경하고 최적화 유무는 CFD를 이용하여 확인하였다. 이 때 노즐 출구의 경계조건은 예비설계프로그램이 제시한 노즐 출구의 정압(P₂)인 10.249 MPa을 사용하였으며, 그 외 경계조건 및 난류모델의 설정 등은 전술한 바와 같다.

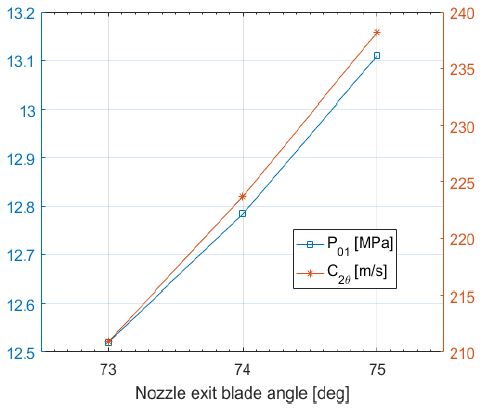
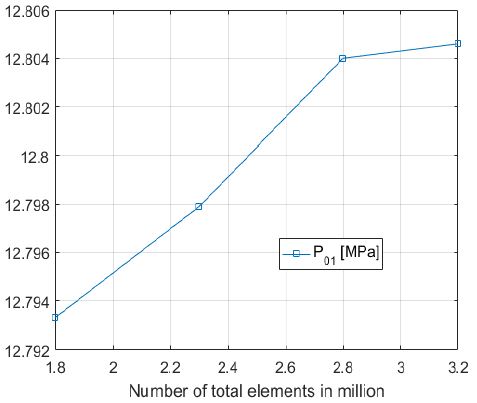
Figure 7은 노즐 출구 깃의 각도 변화에 따른 노즐 입구의 전압(P₀₁)과 노즐 출구의 접선방향 절대속도(C_2θ)의 변화를 나타내고 있다. 예비설계프로그램이 제시한 노즐 입구의 전압(P₀₁)과 노즐 출구의 접선방향 절대속도C_2θ)는 각각 13.0 MPa과 211.53 m/s이다. Figure 7의 결과를 살펴보면, α_2b가 74 °일 때 상기 두 변수는 각각 적절한 값을 가진다. α_2b가 74 °일 때 P₀₁을 기준으로 격자의존성 점검을 수행한 결과는 Figure 8과 같다. 격자수에 의존적이지 않은 결과는 노즐의 격자가 약 3.2 백만 개에서 얻을 수 있었다. 이 때 P₀₁과 C_2θ는 각각 12.81 MPa과 224.36 m/s 이다.

Figure 7

CFD results according to the nozzle exit blade angle(α2b) of the radial outflow turbine

Figure 8

Mesh convergence test results of the nozzle

4.3 로터 속도삼각형의 최적화

로터 입·출구의 속도삼각형은 노즐과 밀접한 관계를 갖는다. 그러므로 노즐 깃의 최적화에 의해 노즐 출구 각도가 74 °로 조정된 노즐 깃은 로터 깃의 최적화에 대한 CFD 해석에 포함되어야 하며, 경계조건의 설정 및 CFD 해석기법은 3.2절에서 부연한 바와 동일하다.

노즐 깃의 최적화에 의해 로터 깃의 입구각도 β_2b는 -21.05 °로 수정되었으며, 로터 깃의 최적화에서는 C_3θ를 제거하기 위하여 로터 출구 측 각도(β_3b)를 조정하였다.

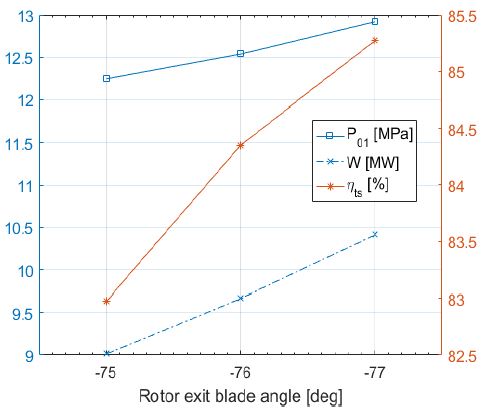
β_3b의 변화에 따른 P₀₁, $W ˙$ 및 η_ts의 변화는 Figure 9와 같다. β_3b가 -77 °일 경우 각 종속변수들은 설계조건에 매우 근사하다. β_3b가 -77 °일 경우 설계조건과 CFD 해석결과를 비교한 것은 Table 4와 같다.

Figure 9

CFD results according to the rotor exit blade angle(β3b) of the radial outflow turbine

Table 4

Comparison between design requirements and CFD results at β3b = -77˚

5. 최종 성능평가

5.1 최종형상

전술한 최적화 과정을 통해 최종 도출된 외향 반경류 터빈의 형상에 대한 주요 제원은 Table 5와 같다. Table 5에서 보인 바와 같이 최적화 과정을 통하여 오로지 노즐 출구 각도와 로터 입·출구 각도가 각각 수정되었음을 알 수 있다.

Table 5

Comparison between results of preliminary design and optimization

5.2 격자의존성 점검

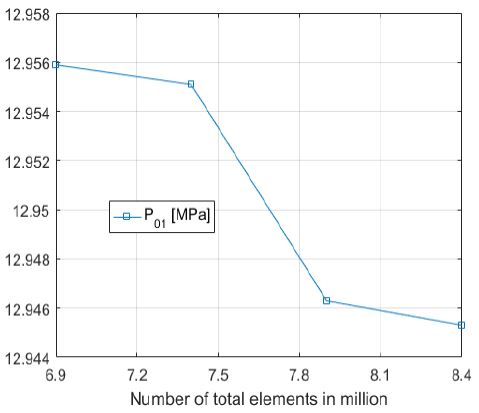
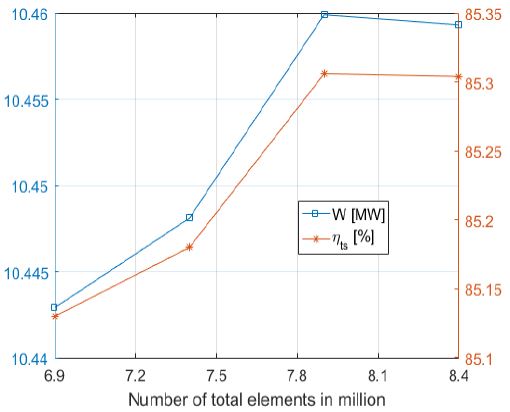
Table 5의 최종형상을 토대로 격자의존성 점검을 실시하였다. 격자의존성 점검 결과는 Figure 10, Figure 11과 같다. 최종 격자는 약 8.4 백만 개이며, 격자계에 대한 보다 상세한 정보는 Table 6과 같다.

Figure 10

Convergence test results of the final radial outflow turbine (P01)

Figure 11

Convergence test results of the final radial outflow turbine (W˙ & ηts)

Table 6

Information of final grid

5.3 최종 성능

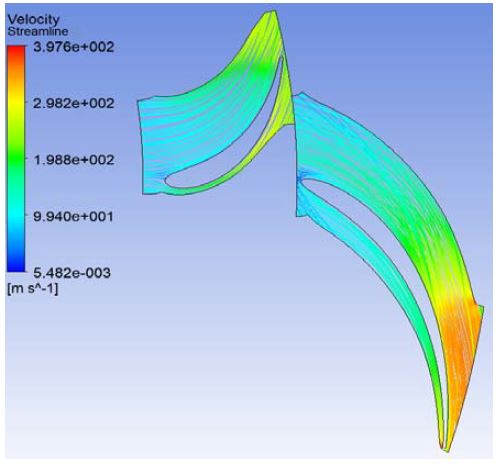
Figure 12는 설계조건에 대한 외향 반경류 터빈의 유선을 나타내고 있다. Figure 12와 같이 지배적인 분리점이나 재순환 영역을 발견할 수 없다.

Figure 12

Streamline of the radial outflow turbine

Table 7은 설계조건과 본 연구에서 설계한 외향 반경류 터빈의 성능을 비교한 것이다. CFD 해석결과를 살펴보면 본 연구에서 설계한 외향 반경류 터빈의 성능은 설계조건과 잘 일치한다.

Table 7

Performance of the radial outflow turbine

그러나 압력비와 온도비가 설계조건과 잘 일치함에도 불구하고, 수치해석결과에 의하면 본 연구에서 설계한 외향 반경류 터빈의 효율은 목표 설계 효율을 다소 상회한다. 이 문제는 ANSYS-CFX의 본질적인 문제로 판단된다. E. Sauret and Y. Gu[20]는 CFX가 사용하고 있는 상태방정식과 엔탈피 및 엔트로피 예측모델이 내재적인 오차를 수반하여 CFX는 터빈의 효율을 실제보다 높게 예측한다고 밝혔다. 보다 구체적으로 상기의 내재적인 오차의 원인은 경미한 온도의 차이에 엔탈피 및 엔트로피가 민감하게 반응하는 실제기체의 특성 때문이다. 즉, 본 연구에서 설계한 외향 반경류 터빈의 예측효율은 설계조건을 5.30 % 상회하나 실제의 경우 이러한 오차는 다소 줄어들 것으로 판단된다.

6. 결 론

본 연구에서 제시한 외향 반경류 터빈용 예비설계알고리즘은 목표 효율을 입력변수로 사용하여, 설계목표에 적합한 터빈의 형상을 제시하도록 개발되었다.

예비설계프로그램의 검증을 위하여 CFD를 수행한 결과, 설계목표에 다소 미흡한 결과를 보였다. 이러한 원인은 예비설계단계에서 노즐과 로터 깃의 편향각을 고려하지 않았기 때문이다. 이러한 결과는 외향 반경류 터빈의 설계에 있어 편향각이 중요하다는 것을 의미한다. 그러나 외향 반경류 터빈의 편향각에 대한 연구는 전무하다. 그러므로 본 연구에서는 터빈의 설계목표가 달성될 수 있도록 편향각을 고려하여 노즐 깃과 로터 깃의 최적화를 수행하였으며, 그 결과 설계조건에 근사한 최종형상을 얻을 수 있었다.

향후에는 본 연구에서 수행한 기초연구를 바탕으로 예비설계프로그램에 편향각 산정모델을 반영할 계획이다.

Nomenclature


A :	area [m²]
C :	absolute velocity [m/s]
C₀ :	spouting velocity [m/s]
C_L :	lift coefficient
c :	true chord length [mm]
f :	correction coefficient
H :	height [mm]
h :	enthalpy [J/kg]
I :	rothalpy [J/kg]
K :	loss coefficient
k :	specific heat ratio
M :	Mach number
$m ˙$ :	mass flow rate [kg/s]
P :	pressure [MPa]
PR :	pressure ratio
R :	gas constant [kJ/kmol∙K]
Re :	Reynolds number
r :	radius [mm]
s :	pitch [mm]
T :	temperature [K]
TR :	temperature ratio
U :	peripheral velocity [m/s]
V :	specific volume [m³/kg]
W :	relative velocity [m/s]
$W ˙$ :	power [MW]

Greeks


α :	absolute flow angle [°]
β :	relative flow angle [°]
η :	efficiency [%]
ν :	velocity ratio
ρ :	density [kg/m³]
ψ :	loading coefficient
ω :	angular velocity [rad/s], acentric factor

Subscripts


0 :	total state
00 :	total state at station 0
1 :	parameter at the nozzle inlet
2 :	parameter at the nozzle exit and rotor inlet
3 :	parameter at the rotor exit
AS :	aspect ratio
accel :	accelerating
b :	blade
c :	critical point parameter
m :	meridional component
N :	nozzle
P :	profile
R :	rotor
Re :	Reynolds number
r :	relative
ref :	reference value
Sec :	secondary
s :	isentropic
sh :	shock
ts :	total to static
tt :	total to total
θ :	tangential component

Acknowledgments

이 논문은 2017학년도 한국해양대학교 신진교수정착연구비 지원을 받아 수행된 연구임.

Author Contributions

Investigation, J. S. Kim and D. Y. Kim; Methodology, J. S. Kim, Y. T. Kim and D. Y. Kim; Numerical Simulation, J. S. Kim; Writing-Original Draft, J. S. Kim; Writing-Review & Editing, Y. T. Kim and D. Y. Kim; Supervision, D. Y. Kim; Funding Acquisition, D. Y. Kim;

References

J. S. Kim, D. Y. Kim, and Y. T. Kim, “Experiment on radial inflow turbines and performance prediction using deep neural network for the organic Rankine cycle,” Applied Thermal Engineering, vol. 149, pp. 633-643, 2019.
J. S. Kim, J. H. Yi, and Y. T. Kim, “Thermodynamic analysis and optimization of a transcritical carbon dioxide Rankine cycle for ocean thermal energy conversion,” Transactions of the Korean Society of Mechanical Engineers B, vol. 42, no. 11, pp. 721-733, 2018. (in Korean).
D. Y. Kim and Y. T. Kim, “Preliminary design and performance analysis of a radial inflow turbine for organic Rankine cycles,” Applied Thermal Engineering, vol. 120, pp. 549-559, 2017.
Y. Wang, X. Tan, N. Wang, and D. Huang, “Aerodynamic design and numerical study for centrifugal turbine with different shapes of volutes,” Applied Thermal Engineering, vol. 131, pp. 472-485, 2018.
J. Bao and L. Zhao, “A review of working fluid and expander selections for organic Rankine cycle,” Renewable and Sustainable Energy Reviews, vol. 24, pp. 325-342, 2013.
C. Spadacini and D. Rizzi, “Radial outflow turbines for Organic Rankine Cycle expanders,” in Organic Rankine Cycle (ORC) Power Systems, Elsevier, 2017, pp. 335-359, 2017.
A. M. Al Jubori, R. K. Al-dadah, S. Mahmoud, and A. Daabo, “Modelling and parametric analysis of small-scale axial and radial-outflow turbines for Organic Rankine Cycle applications,” Applied Energy, vol. 190, pp. 981-996, 2017.
D. Luo, Y. Liu, X. Sun, and D. Huang, “The design and analysis of supercritical carbon dioxide centrifugal turbine,” Applied Thermal Engineering, vol. 127, pp. 527-535, 2017.
C. Spadacini, L. Centemeri, M. Danieli, D. Rizzi, and L. Xodo, “Geothermal Energy Exploitation with the Organic Radial Outflow Turbine,” Proceedings World Geothermal Congress, pp. 1-6, 2015.
D. Maksiuta, L. Moroz, M. Burlaka, and Y. Govoruschenko, “Study on applicability of radial-outflow turbine for 3MW WHR organic Rankine cycle,” Energy Procedia, vol. 129, pp. 293-300, 2017.
D. Y. Kim and Y. T. Kim, “Preliminary design and performance analysis of a radial inflow turbine for ocean thermal energy conversion,” Renewable Energy, vol. 106, pp. 255-263, 2017.
E. Casati, S. Vitale, M. Pini, G. Persico, and P. Colonna, “Centrifugal turbines for mini-organic Rankine cycle power systems,” Journal of Engineering for Gas Turbines and Power, vol. 136, p. 122607, 2014.
A. T. Sayers, Hydraulic and Compressible Flow Turbomachines, McGraw-Hill, 1990.
Mathworks MATLAB Manual, 2016.
H. Moustapha, M. F. Zelesky, N. C. Baines, and D. Japikse, Axial and Radial Turbines, Concepts NREC, 2003.
R. H. Aungier, Turbine Aerodynamics, NY, USA: ASME Press, 2006.
D. G. Ainley and G. C. R. Mathieson, “A method of performance estimation for axial-flow turbines,” Aeronautical Research Council Reports and Memoranda no. 2974, 1951.
ANSYS CFX 13.0 Modeling Guide, 2010.
ANSYS CFX 13.0 Theory Guide, 2010.
E. Sauret and Y. Gu, “Three-dimensional off-design numerical analysis of an organic Rankine cycle radial-inflow turbine,” Applied Energy, vol. 135, pp. 202-211, 2014.

Parameters	Preliminary design	CFD
P₀₁ [MPa]	13.00	11.08
$W ˙$ [MW]	10.00	6.50
η_ts [%]	80.00	77.50
α₂ [°]	66.87	60.89
β₃ [°]	-74.10	-72.11
C₂ [m/s]	230.01	205.35
C_2θ [m/s]	211.53	177.52
C_3θ [m/s]	0	32.86

Parameters	Preliminary design	CFD
P₀₁ [MPa]	13.00	12.92
$W ˙$ [MW]	10.00	10.41
η_ts [%]	80.00	85.27

Parameters	Preliminary design	Optimization results
r₁ [mm]	345.393	345.393
r_2N [mm]	408.392	408.392
r_2R [mm]	412.392	412.392
r₃ [mm]	504.560	504.560
H [mm]	10.843	10.843
α_1b [°]	0	0
α_2b [°]	66.87	74.0
β_2b [°]	27.78	-21.05
β_3b [°]	74.10	-77.0

Domain	No. element	max. y+
Nozzle	4,093,581	22.84
Rotor	4,082,892	25.67

Parameters	design value	CFD
PR_ts [-]	1.63	1.62
TR_ts [-]	1.08	1.07
$W ˙$ [MW]	10.00	10.46
η_ts [%]	80.00	85.30

Parameters	Units	Values
$W ˙$	MW	10.0
$m ˙$	kg/s	182.46
P₀₁	MPa	13.0
T₀₁	K	773.0
η_tt	%	85.0
η_ts	%	80.0
RPM	rev/min	6,000

Parameters	Units	Values
r₁	mm	345.393
r_2N	mm	408.392
r_2R	mm	412.392
r₃	mm	504.560
H	mm	10.843
α_1b	°	0
α_2b	°	66.87
β_2b	°	-27.78
β_3b	°	-74.10