벌브 수차 가이드베인 개도 변화의 영향에 관한 수치해석
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 가이드베인 개도 변화에 따른 벌브 수차의 성능을 확인하기 위하여, 이동격자기법을 이용하여 수차의 성능을 분석하는 방법을 정립하고, 이를 이용하여 시간에 따른 가이드베인 개도의 연속적인 변화과정을 수치모사하였다. 본 해석의 경우, 설계 사양에 따라 이론적으로 최적화 설계된 실물 수차 모델의 부근의 가이드베인 개도 57˚, 61.5˚, 66˚의 3가지 경우에 대해서 수차 모델을 분석하였다. 비정상상태 수치해석 결과, 정격 수두 9.2m, 회전수 171rpm, 가이드베인 개도 61.5˚일 때, 최대효율 89%로 확인되었으며, 가이드베인과 로터 사이의 유동장에서 수차 회전주파수의 4X에 해당되는 11.33Hz에서 가장 강한 맥동이 확인되었다. 흡출관에서는 와류로 인한 압력맥동이 확인되었으나 맥동 폭의 절대적인 크기는 BPF에서 발생하는 3000~3400Pa2/Hz에 비해 매우 작은 150~180Pa2/Hz 수준인 것으로 확인되었다.
Abstract
In this study, a method for analyzing fluid flow characteristics using the moving mesh method is established to evaluate the performance of a bulb turbine with changes in the degree of guide vane opening. Using this method, we numerically simulated the continuous change process of the guide vane opening over time. The turbine model was analyzed for three cases of the guide vanes, i.e., 57 degrees, 61.5 degrees, and 66 degrees, in a real turbine model that was theoretically optimized according to design specifications. The unsteady-state numerical analysis confirmed that the maximum efficiency was 89% when the rated head was 9.2 m, the number of revolutions was 171 rpm, and the guide vane was 61.5 degrees. In the flow field between the guide vane and the rotor, the strongest pulsation was observed at 11.33 Hz, which corresponds to four times the turbine rotation frequency. In addition, the pressure pulsation due to the vortex was observed in the draft tube, but the absolute magnitude of pulsation was between 150 and 180 Pa2/Hz, which is very small compared with the one generated in the blade passing frequency between 3000 and 3400 Pa2/Hz.
Keywords:
Bulb turbine, Computational fluid dynamics(CFD), Moving mesh method, Guide vane opening, Efficiency, Vibration키워드:
벌브 터빈, 전산유체역학, 이동격자기법, 가이드베인 개도, 효율, 진동1. 서 론
벌브 수차는 가이드베인 개도와 수차 블레이드의 개도가 동시에 변화가 가능하여 운전조건이 다양하게 존재한다. 수차의 성능을 검증하기 위하여 모형 수차 성능시험에서는 전체 운전 구간을 일정한 가이드베인 개도에 따라 수차의 성능을 검증한다[1]. 일반적으로 수치해석에서도 모델 시험방법과 동일하게 일정한 가이드베인 개도의 간격으로 출력, 효율 등 수차의 성능을 분석하며 관련된 연구는 이미 많이 진행되었다[2]-[6]. 이러한 일반적인 해석 방법으로는 가이드베인 개도에 따라 수치해석 전처리 단계에서 모델링과 격자를 생성하는 시간이 많이 소요되고 또한 가이드베인 개도별로 해석 모델이 다양하여 수치해석 시간도 많이 소요된다. 이동격자기법(Moving mesh method)으로 시간에 따라 가이드베인 개도를 연속적으로 변화시킬 수 있지만 격자의 위치 변화로 인하여 격자는 찌그러지거나 꼬이는 현상이 발생할 수도 있어 격자에 대한 의존도가 높고 또한 각각의 가이드베인 회전 좌표축에 대한 설정과 격자를 이동하기 위한 사용자의 수식에 대한 정의가 필요하여 수차에 관련된 연구에서는 이동격자기법을 많이 사용하지 않았다[7][8]. 그러나 일정 가이드베인 간격 또는 요구되는 각도에 따라서는 연속적인 이동격자기법을 적용하여 전처리와 해석에서 소요되는 시간적 문제점들을 극복할 수 있다.
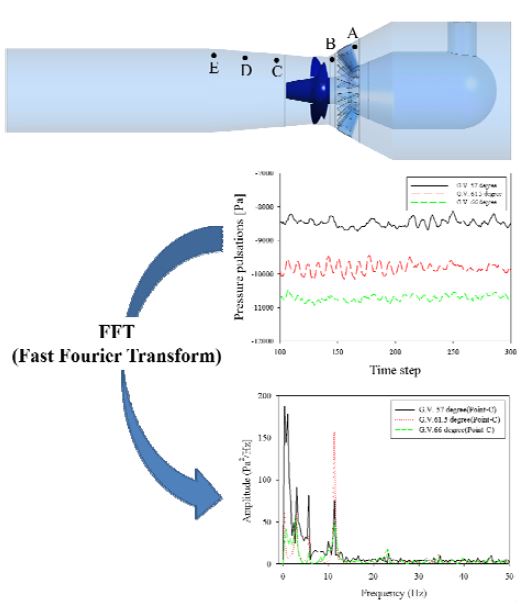
본 연구에서는 가이드베인 개도에 따른 수차의 성능을 신속하게 검증하기 위하여, 해석 모델을 줄이고 해석 시간을 단축할 수 있는 이동격자기법을 적용하여 해석하는 방법을 확립하고, 가이드베인 개도 변화에 따른 유동특성을 연속적으로 해석하여 수차의 출력과 효율을 계산하였다. 또한, 유체력에 의한 실물 수차의 진동을 해석하가 위하여 압력맥동을 고속 Fourier 변환(Fast Fourier Transform, FFT)을 행하여 수차의 성능을 검증하였다.
2. 수치해석
2.1 모델링 및 격자생성
본 연구에서 검증되는 실물 수차의 모델은 정격수두 9.2m, 정격유량 75.3m3/s, 정격출력 6MW, 회전수 171rpm의 수차 설계 사양에 따라 블레이드 개수와 날개의 형상들을 이론적으로 최적화 설계하여 도출된 실물 수차 모델이다. 최적화 설계된 블레이드의 개도는 26˚, 블레이드 개수는 4개이며, 가이드베인 개수는 총 16개로 설계되었다. 최대효율은 가이드베인 개도 61.5˚일 때 나타난다. 따라서 본 연구는 가이드베인 개도 61.5˚를 기준으로 전후 4.5˚간격으로 57˚, 61.5˚, 66˚에 대한 총 3개 모델을 분석하였다.
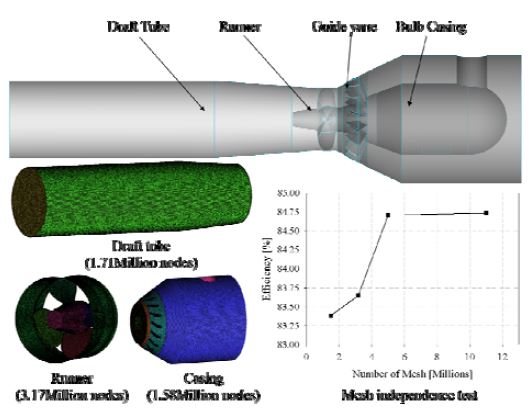
Figure 1과 같이 유동장 모델링은 케이싱, 가이드베인, 러너와 흡출관 총 4개의 유동영역으로 구성이 되었다. ICEM CFD를 이용하여 테트라(Tetra) 격자를 생성하였으며 모든 벽면에는 프리즘(Prism) 격자를 생성하였다. 격자수에 따른 효율 변화에 대한 격자 의존성을 확인하여 본 수치해석에 사용되는 총 격자수는 약 500만 개이다.
2.2 경계조건 및 해석조건
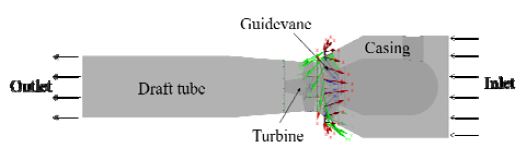
Figure 2와 같이 입구는 전압(Total pressure)의 경계조건으로 설정하였고, 출구는 정압(Static pressure) 조건으로 대기압으로 설정하였다. 수차의 회전 현상을 구현하기 위하여 회전수는 171rpm으로 가정하였고, 고정자와 회전자가 접하는 면을 Transient Rotor Stator의 Interface Model 기법으로 인터페이스(Interface)로 설정하였다.
Table 1과 같이 수치해석은 비정상상태로 해석하였으며, 작동유체는 25˚C 물로 가정하였고 난류 모델은 SST 난류 모델을 사용하였다. 모든 벽면은 No-slip 조건을 설정하였다.
2.3 가이드베인 벽면 회전 운동
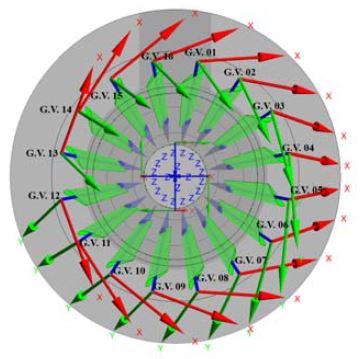
Figure 3과 같이 시간에 따른 가이드베인 개도의 변화를 구현하기 위하여 총 16개 가이드베인에 각각의 로컬 좌표계(Local Coordinate)를 적용하여 Z 축을 회전축으로 설정하였다.
수식을 정의하는 CFX Expressions를 이용하여 가이드베인 개도 57˚, 61.5˚, 66˚에서 연속적으로 변화될 수 있도록 시간의 함수로 정의하였다. 수치해석은 0.01초의 시간 간격으로 57˚에서 충분히 수렴이 되는 해를 얻은 후, 다음 각도로 이동하여 순차적으로 해석을 수행하였다.
식 (1)과 같이 격자의 크기에 따라 Increase Near Small Volume 기법[9]으로 격자의 강성(Stiffness)을 설정하여 이동 격자의 변형을 최소화하였다.
| (1) |
여기서 Γdisp는 격자 강성, Vref는 기존 격자 크기, V는 유동영역 격자의 크기, Cstiff는 강성계수이다.
3. 해석 결과 분석
본 연구는 이론적으로 최적화 설계된 벌브형 실물 수차에 대해 가이드베인 개도에 따른 유동특성을 분석하여 출력과 효율에 관한 성능을 검증하고 흡출관내의 와류 현상과 유체력에 의한 수차의 진동 특성을 동시에 분석하였다.
3.1 수차 출력 및 효율 분석
수차의 출력 Pt는 식 (2)과 같다.
| (2) |
여기서 T는 토크, ω는 수차 회전수이다.
수차의 효율은 식 (3)과 같다. 여기서 η는 수차 효율, Pt 수차의 출력, Pth은 수력 에너지 입력이다.
| (3) |
수력 에너지 입력은 식 (4)와 같다. 여기서 ρ는 유체의 밀도, g는 중력 가속도, Q는 체적 유량, H는 유효 낙차이다.
| (4) |
유효 낙차는 식 (5)와 같다. 여기서 pi는 입구 전압, po는 출구 전압이다.
| (5) |
Figure 4와 같이 수차의 최대효율은 가이드베인 개도 61.5˚에서 가장 높은 89%로 확인되었고, 가이드베인 개도 57˚와 66˚에서는 각각 88.1%, 88.5%인 것으로 확인되었다.
수차의 단위 유량과 단위 출력은 식 (6), 식 (7)과 같다.
여기서 D는 수차의 직경이다.
| (6) |
| (7) |
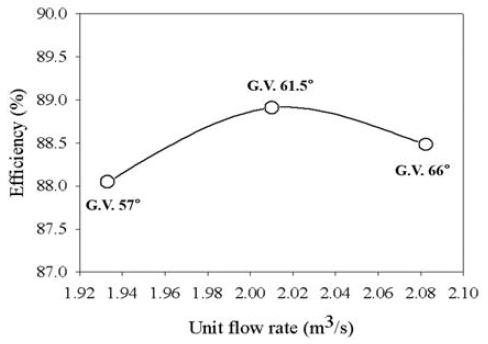
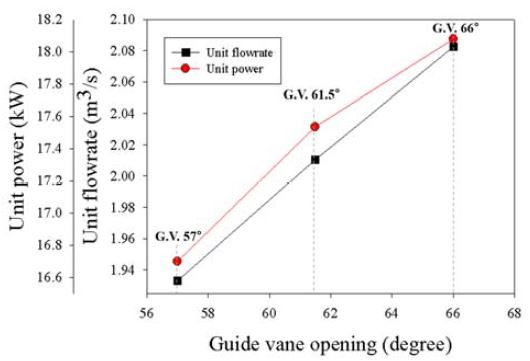
Figure 5에서 가이드베인 개도에 따라 단위 유량과 단위 출력을 비교하였다. 가이드베인 개도 61.5˚는 최대효율점 BEP(Best Efficiency Point)의 설계조건이며 이때의 단위 유량(QBEP)은 2.01m3/s, 단위 출력(PBEP)은 17.54kW으로 확인되었다. 가이드베인 개도 57˚에서의 단위 유량은 0.96QBEP, 단위 출력은 0.95PBEP이며, 가이드베인 개도 66˚에서의 단위 유량은 1.04QBEP, 단위 출력은 1.03PBEP이다. 가이드베인 개도의 증가에 따라 유량과 출력이 동시에 증가한다. 가이드베인 개도에 따른 효율은 출력 대 유량비 λ(P11/Q11)로 결정되며 가이드베인 개도 61.5˚에서 λ는 가장 크고 가이드베인 개도 66˚, 57˚에서 λ의 값은 순차적으로 감소한다. 따라서 가이드베인 개도 61.5˚에서 효율이 가장 높고 가이드베인 개도 57˚에서 효율이 가장 낮게 나타난 것으로 판단된다.
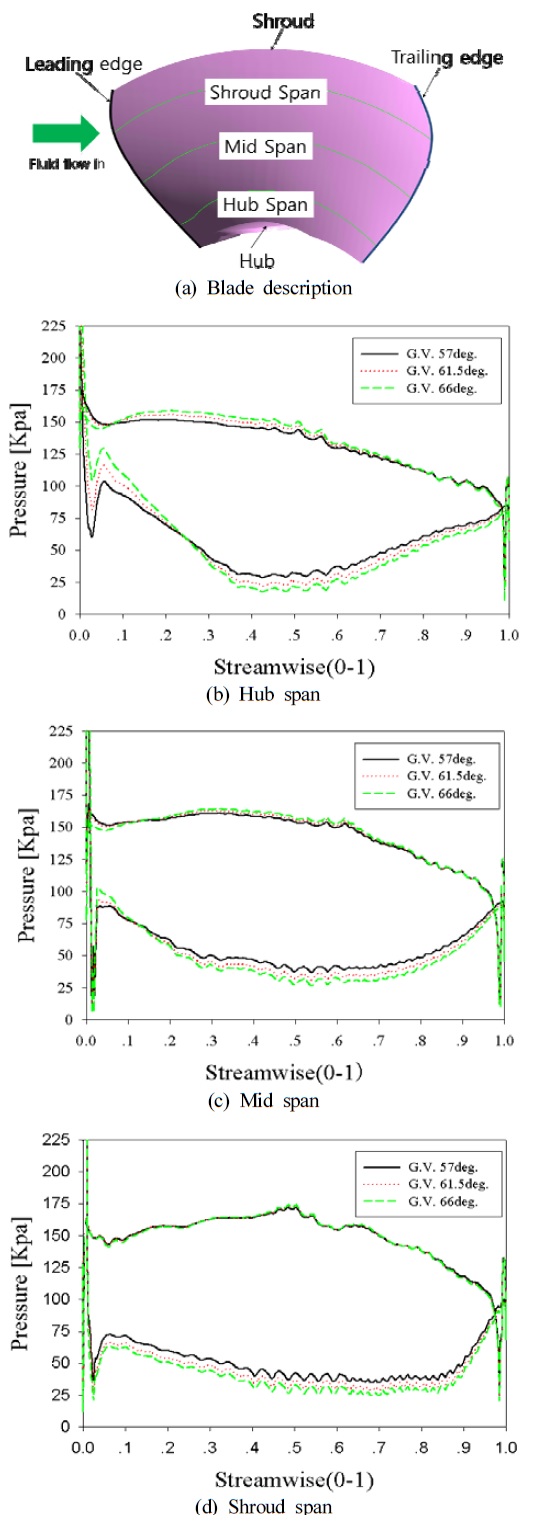
블레이드의 압력분포 특성을 분석하기 위해 Figure 6과 같이 수차 블레이드의 허브(Hub), 중간(Mid) 및 쉬라우드(Shroud) 스팬(span)의 단면에서 유동방향에 따른 압력 분포를 비교하였다. 여기서 Figure 6 (a)와 같이 x 축의 0은 전연(Leading edge, LE), 1은 후연(Trailing edge, TE)을 나타내며, y 축은 각 스팬의 위치별 압력 값을 의미한다. 허브 스팬 Figure 6 (b)과 같이 블레이드 전연에서 유선방향으로 0~0.2에서는 가이드베인 개도의 증가에 따라 압력면(Pressure side)의 압력은 감소하고 흡입면(Suction side)의 압력은 증가하여 압력차는 감소한다. 유선방향으로 0.2~1에서의 가이드베인 개도의 증가에 따라 압력면과 흡입면의 압력차는 증가한다. 중간 스팬 Figure 6 (c)과 같이 블레이드 전연 유선방향으로 0~0.1에서는 가이드베인 개도의 증가에 따라 압력면(Pressure side)의 압력은 감소하고 유선방향으로 0.1~1에서의 압력차는 증가한다. 쉬라우드 스팬 Figure 6 (d)과 같이 유선방향으로 0~1의 전체 구간에서 가이드베인 개도의 증가에 따라 압력면과 흡입면의 압력차는 증가한다. 블레이드의 허브와 중간 스팬의 전연에서 압력차는 일부 감소하는 경향은 확인되었으나 전반적으로 가이드베인 개도에 따라 압력차는 증가하여 수차의 출력은 증가한 것으로 판단된다.
3.2 유동장 와류 현상
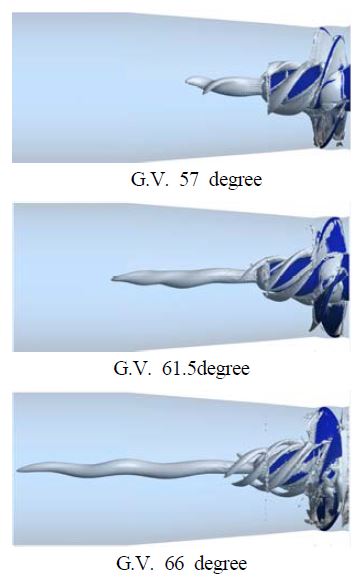
와도는 속도 벡터의 컬(curl)로 정의되어 유동 영역의 회전상태를 확인할 수 있다. Figure 7과 같이 동일한 와도 레벨 7.36s-1을 설정하여 가이드베인 개도의 변화에 따른 수차 블레이드와 흡출관내에서 발생하는 와류 현상을 가시화하여 비교하였다. 유동장 내부의 위치별 와류의 특성은 블레이드 허브 근처와 흡출관 중심부에서 상대적으로 큰 와류가 발생하였다. 가이드베인 개도의 변화에 따른 와류의 특성은 가이드베인 개도의 증가에 따라 흡출관내의 와류의 지름은 점차 감소하고 와류는 출구 방향으로 스트레칭(Stretching)되어 와류의 길이는 증가한다.
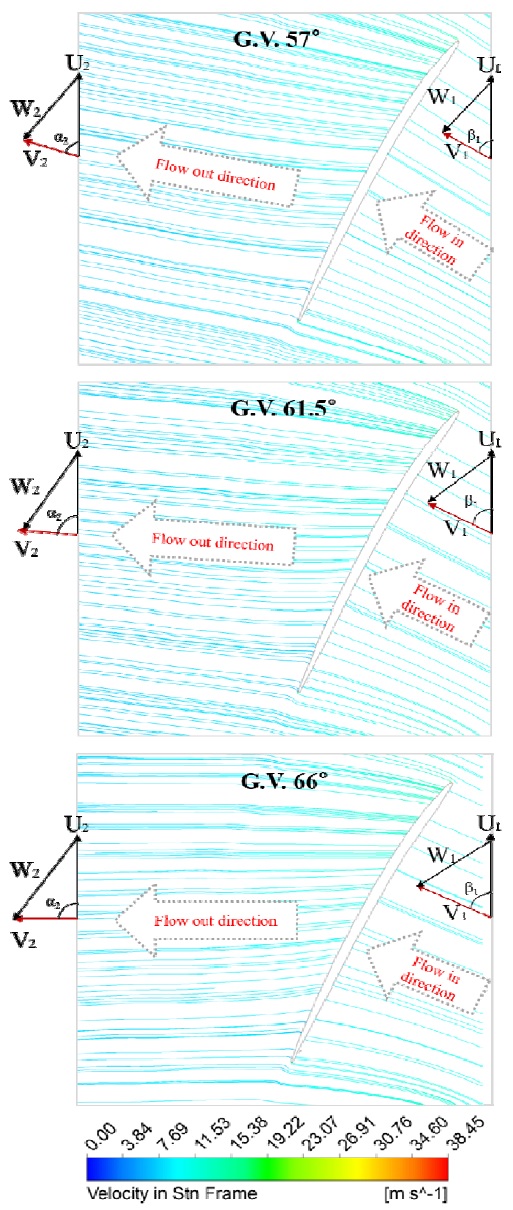
Figure 8과 같이 수차 블레이드의 중간 스팬(span) 단면의 와류 현상을 유선(Streamline)으로 분석하였다. 여기서 U는 블레이드의 회전속도, V는 절대속도, W는 상대속도를 나타내며, 1은 블레이드 입구, 2는 블레이드 출구를 의미한다. 여기서 블레이드의 회전속도 U는 일정하다. 가드베인 개도의 증가에 따라 V1과 U1의 각도 β1은 증가하여 상대속도 W1도 동시에 변화한다. 이러한 변화는 블레이드 출구단 유체의 절대속도 V2의 방향에도 영향을 준다. 즉, 가이드베인 개도의 증가에 따라 U2와 V1 사이의 각도 α2는 점차 커져 절대속도V2의 방향은 회전축 방향과 근접하여 유체의 회전방향 속도 성분은 상대적으로 감소한다. 따라서 가이드베인 개도의 증가에 따라 유체는 회전축의 방향으로 블레이드의 후단을 통과하기 때문에 흡출관내의 와류는 감소한 것으로 판단된다.
3.3 수력학적 진동 분석
수력발전소의 수차의 진동 원인은 크게 기계적 원인, 수력학적 원인, 전기적 원인으로 분류가 된다. 그 중, 수력학적 진동은 압력맥동, Karman 와동(Karman Vortex), 캐비테이션, 흡출관내의 볼텍스 로프 등의 유동현상이 원인이며, 이로 인하여 진동이 발생한다. 본 연구는 Figure 9와 같이 가이드베인 입구 A, 수차 블레이드 입구 B, 흡출관 C, D, E 총 5개 위치에 대한 압력을 측정하여 유체력의 압력 맥동에 따른 수차의 진동을 분석하였다.
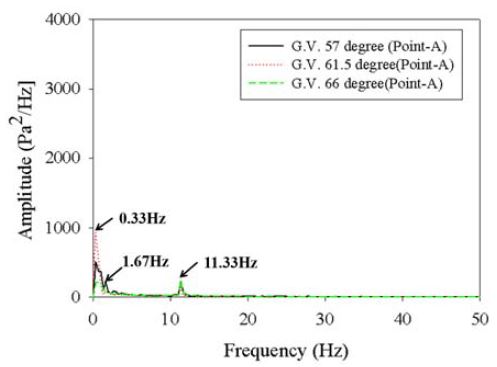
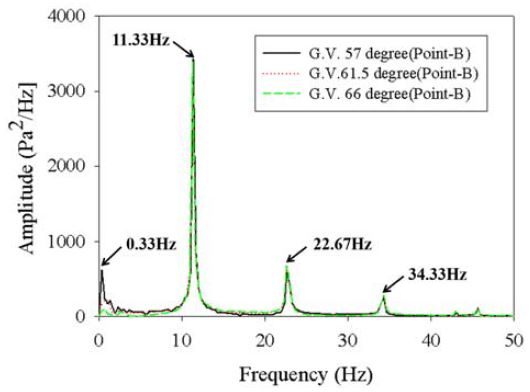
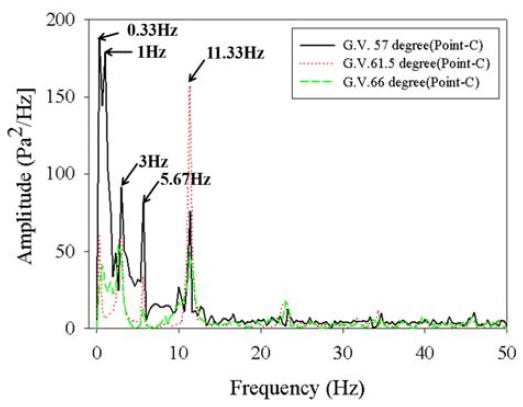
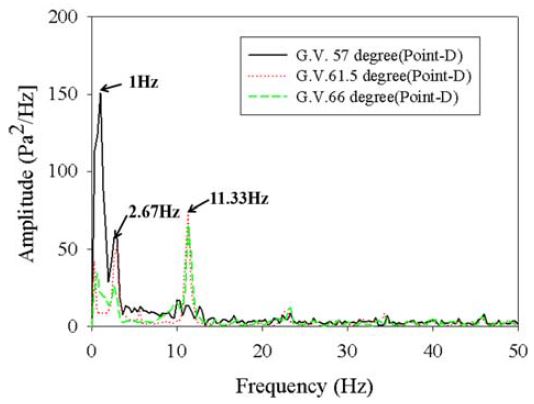
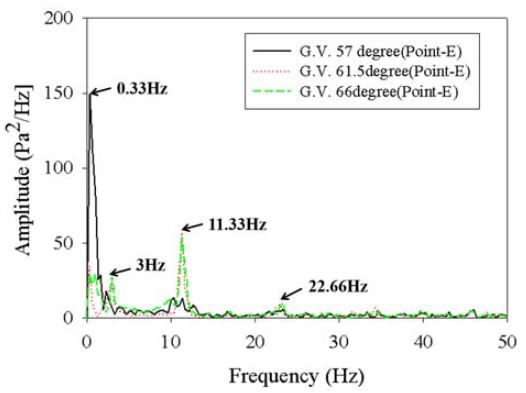
Figure 10 ~ Figure 14와 같이 가이드베인 입구(Point-A), 러너 입구(Point-B), 흡출관 출구(Point-C, D, E) 총 5개 위치에 대한 시간에 따른 압력맥동을 FFT 변환을 행하여 유체력에 의한 진동을 분석하였다.
A 지점에서 관찰되는 11.33Hz 압력맥동은 러너에 의한 BPF(Blade Passing Frequency)로 수차 회전수의 4X로 나타났다. 여기서 수차의 회전주파수 X는 2.85Hz(171rpm/60)이다. 11.33Hz 압력맥동에 대한 진폭의 값은 Table 2와 같다. BPF 압력맥동은 러너가 위치한 B 지점에서 3428Pa2/Hz로 가장 높게 나타났으며 러너 전방인 A 지점과 후방 C 지점에서는 각각 245, 157Pa2/Hz 수준이었다. B 지점에서는 BPF의 2배(8X), 3배(12X) 압력맥동도 함께 관찰되었다. BPF에 의한 압력맥동은 러너에서 멀어질수록 낮아져 각각 C, D, E 지점에서는 각각 157, 73, 57Pa2/Hz 수준을 나타냈다. BPF 압력맥동은 BEP 구간에서 3097Pa2/Hz로 가장 낮았으며 BEP 이하(G.V.57˚)/이상(G.V.66˚) 구간에서는 3400Pa2/Hz 안팎으로 BEP보다 다소 높은 수준을 보였다.
또한 러너를 통과한 이후인 C, D 지점에서는 일부 운전조건에서 1Hz 압력맥동이 관찰되었다. Table 3과 같이 1Hz 압력맥동은 가이드베인 개도 57˚에서 두드러지게 관찰되었는데 이는 통상적으로 VIV(Vortex Induced Vibration)가 발생하는 주파수 범위인[10] 0.57~1.14Hz, (0.2~0.4X)에 부합하기에 C, D 지점에서의 1Hz 압력맥동은 와류에 의한 진동일 가능성이 있다. 다만, 맥동 폭의 절대적인 크기는 150~180Pa2/Hz이지만 맥동 폭의 상대적인 크기(Δp/Pth)는0.17~0.2%인 매우 낮은 수준이다.
4. 결 론
본 연구에서는 이동격자기법을 이용하여 연속적인 가이드베인 개도 변화에 따른 수차 성능을 검증할 수 있는 수치해석적 방법을 확립하고, 연속적인 가이드베인 개도 변화( 57˚, 61.5˚, 66˚)에 대한 수차의 출력, 유량, 효율을 분석하여 다음과 같은 결론을 얻었다.
- (1) 수차의 효율은 출력 대 유량비 λ(P11/Q11)로 결정되어 가이드베인 개도 61.5˚에서 효율이 가장 높고 가이드베인 개도 57˚에서 효율이 가장 낮게 나타났다.
- (2) 가이드베인 개도의 증가에 따라 블레이드를 통과한 유체는 회전축의 방향과 근접하게 블레이드 후단으로부터 흡출관내로 통과하여 와류의 지름은 점차 감소하고 와류의 길이는 스트레칭되어 증가하는 것으로 판단된다.
- (3) 압력맥동은 가이드베인과 로터 사이의 유동장에서 가장 크게 나타났으며, 흡출관에서도 압력맥동이 확인되었으나 맥동 폭의 절대적인 크기는 BPF에서 발생하는 진폭에 비해 매우 작은 수준으로 확인되었다.
Acknowledgments
본 연구는 2016년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제 입니다. (No. 20163010060340)
Author Contributions
Conceptualization, K. M. Li and Y. W. Lee; Methodology, K. M. Li; Software, K. M. Li and W. Kwon; Validation, K. M. Li and Y. W. Lee; Formal Analysis, K. M Li; Investigation, K. M Li; Resources, K. M Li; Data Curation, K. M Li; Writing—Original Draft Preparation, K. M Li and W. Kwon; Writing—Review & Editing, Y. W. Lee; Visualization, K. M. Li; Supervision, Y. W. Lee; Project Administration, K. M. Li; Funding Acquisition, K. M. Li;
References
- IEC 60193 Standard Hydraulic Turbine, Storage Pumps and Pump-Turbine-Model Acceptance Tests, International Electrotecchinic Commision, 1999.
- M. Kaniecki and Z. Krzemianowski, “CFD analysis of high speed Francis hydraulic turbines,” Transactions of the Institute of Fluid-Flow Machinery, no. 131, pp. 111-120, 2016.
- V. L. Vu, Z. M. Chen, and Y. D. Choi, “Study on swirl flow in a draft tube of a bulb hydro turbine model,” Journal of the Korean Society of Marine Engineering, vol. 42, no. 10, pp. 812-817, 2018 (in Korean).
- D. Y. Kim and Y. T. Kim, “Design and performance analysis of a 115kW class bulb-type hydro-turbine,” Journal of the Korean Society of Marine Engineering, vol. 42, no. 4, pp. 304-311, 2018 (in Korean).
- H. Benigni and H. Jaberg, “Stationary and transient numerical simulation of a bulb turbine,” Proceedings of the 5th IASME/WSEAS International Conference on Fluid Mechanics and Aerodynamics, Athens, Greece, pp. 135-140, 2007.
- S. Hotzl, T. Schechtl, P. Rutschmann, and W. Knapp, “Development of a low head tidal turbine part 1: CFD simulation, design and optimization,” International Marine Energy Journal, vol. 1, no. 2, pp. 81-90, 2018.
- J. Nicolle, J. F. Morissette, and A. M. Giroux, “Transient CFD simulation of a Francis turbine startup,” IOP Conference Series Earth and Environmental Science, vol. 15, no. 6, pp. 1-8, 2014.
- X. L. Mao, A. D. Monte, E. Benini, and Y. Zheng, “Numerical study on the internal flow field of a reversible turbine during continuous guide vane closing,” Energies, vol. 10, no. 7, p. 988, 2017.
- J. H. Shin, “Tips for using CFX moving mesh and immersed solid,” ANZINE, TSNE: 2014.
- Y. L. Wu, S. C. Li, S. H. Dou, and D. Qian, Vibration of Hydraulic Machinery, Mechanisms and Machine Science 11, Springer, Dordrecht, Netherlands, 2013.