PSO를 이용한 문자마킹 표면비드 폭에 따른 최적의 공정변수에 대한 연구

2.1 용접실험 구성 및 방법

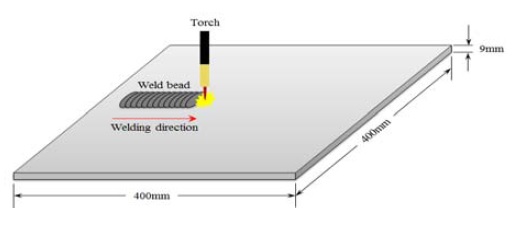
산업구조물 문자마킹 용접부의 품질을 확인하고 최적의 공정변수를 개발하기 위하여 GMA 용접실험을 실시하였으며, 실험을 위하여 600 A급 GMA 용접기 및 용접토치, 토치 크레인, 유압 JIG, 용접 제어부, 3D Scanner 등 전체시스템은 Figure 1에 나타낸 바와 같이 구성하였다. 용접실험에는 ∅1.2의 K-71 플럭스 코어드 와이어 및 CO₂ 100 %의 보호가스가 사용되었으며, 개별적인 봄베를 사용하여 보호가스를 18 l/min으로 고정하여 분사하였다. 고정 변수는 다수의 기존 연구결과를 바탕으로 일반적인 GMA 용접공정에서의 최적조건을 적용하였다. 문자마킹 용접부의 보다 신뢰성 있는 실험 결과분석을 위하여 3D Scanner를 설치하여 PC를 통해 정밀한 용접부 크기를 측정하도록 하였다.

Figure 1

Letter marking GMA welding experimental setup

본 실험을 위하여 일반구조용 압연강재인 SS400 재질의 평판을 사용하였으며, 400×400×9 mm 규격의 시험편을 제작하였다. 문자마킹 용접공정은 산업구조물 외판에 Bead-on-Plate로 용접이 수행되기 때문에 시험편 옆면에 개선각도 및 루트면은 설정하지 않았다.

시험편의 소비를 최소화하기 위하여 안정적인 용접성을 확보할 수 있는 전체 용접길이를 350 mm로 설정하고 제작한 평판 시험편에 3회의 용접실험을 수행하였다. 시험편에 용접하고자 하는 표면부의 녹, 스케일, 산화물 등 이물질이 용접결함의 원인이 되지 않도록 Stainless wire-brush 및 Sand paper #400, #800, #1500 순서로 시험편을 깨끗이 닦아내었다. Figure 2는 문자마킹 GMA 용접공정의 개략도를 나타내며, 시험편의 기계적 성질 및 화학적 조성은 Table 1과 Table 2에 각각 나타내었다.

Figure 2

A schematic diagram for letter marking weld process

Table 1

Mechanical properties of base metal

Table 2

Chemical composition of base metal

본 절에서는 용접공정 변수에 따른 표면비드 형상을 확인하기 위한 목적으로 진행되었으며, 표면비드 형상 변화에 주요 요인이 되는 용접전류, 아크전압, 용접속도, 전극간 거리로 선정하여 문자마킹 용접실험 계획을 수립하였다. 또한 선정된 공정변수는 예비실험을 통하여 안정적인 표면비드가 형성되는 범위 내에서 도출된 적정값인 용접전류 135∼195 A, 아크전압 18∼28 V, 용접속도 400∼800 mm/min, 전극간 거리 12∼18 mm로 선정하였다. 용접실험 계획은 일반적으로 알려진 완전요인실험으로 구성하였으며, 요인설계(Factorial design)의 경우 각각의 입력변수들의 수준을 일정간격으로 배치하여 모든 입력변수들간 수준(Level)의 조합에 의해 실험이 이루어지게 된다. 다시 말하면, 입력변수 및 수준이 많아질 경우 용접실험 결과에서 경향파악 및 비선형적인 변화를 적절하게 대응할 수 있기 때문에 매우 효율적이라고 사료하였다. 따라서, 본 실험에서는 입력변수 변화에 따른 출력변수 반응의 비선형적인 변화에도 민감하게 대응할 수 있고 실험횟수의 최적화를 고려하기 위하여 완전요인설계법 FFD(Full Factorial Design)를 적용하였다. 완전요인설계는 비선형적인 변화를 감지할 수 없는 요인설계의 단점을 보완하기 위하여 기존의 요인배치법의 표본 데이터에 축점(Axial point)을 추가시킨 형태로 실험횟수 N은 식 (1)과 같이 나타낼 수 있다. 여기서 인자의 수가 n이고 각인자의 수준수가 k이다.

수준(Level)은 중심점과 2k 요인배치법의 수준값(-1, 0, 1)을 갖게 됨으로서 3개의 수준을 갖는 실험계획법으로 구성된다. 따라서, 입력변수 k = 4로 설정할 경우 식 (1)에 의해 총 81회의 실험조건이 생성된다. 사전 예비실험을 통하여 도출된 적정 범위값을 바탕으로 입력변수의 실험변수 및 수준은 Table 3과 같이 설정하였으며, 81개의 실험조건을 사용하여, 순차적으로 3회 반복실험을 실시하였다.

Table 3

Welding parameters and their levels

2.2 공정변수 변화에 따른 표면비드 형상의 영향

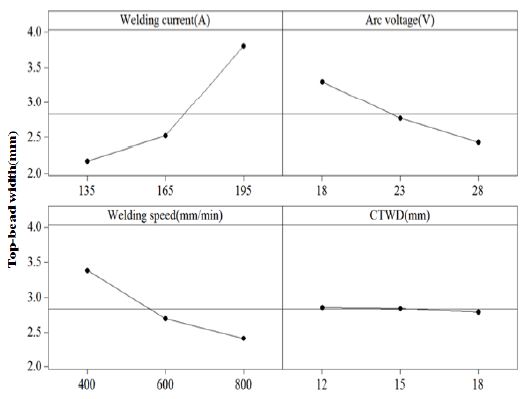
문자마킹 용접공정의 표면비드 형상에 미치는 4가지 변수(용접전류, 아크전압, 용접속도, 전극간 거리)의 영향을 분석하기 위하여 MINITAB프로그램을 이용하여 주효과도 분석을 수행하였다. Figure 3에 나타낸 바와 같이 표면비드 폭은 용접공정 변수에 의해 영향을 받으며, 용접전류가 증가함에 따라 표면비드 폭이 증가함을 확인하였다. 또한 아크전압 및 용접속도가 증가함에 따라 표면비드 폭이 감소함을 확인하였으며, 이는 아크전압이 증가할수록 모재 용융량이 동반으로 증가하기 때문에 시험편 표면부에 와이어의 용착이 어려워져 표면비드 폭이 감소하는 것으로 확인된다. 용접속도가 빠를 경우 와이어가 용착될 시간이 부족하여 표면 비드가 쌓일 시간이 충분치 못하기 때문에 표면비드 형상이 전반적으로 감소되는 것을 확인하였다. 반면에 전극간 거리인 CTWD의 경우 표면비드 폭에 미치는 영향이 가장 미비한 것으로 확인되어 표면비드 형상 예측모델을 개발하는데 제외시켜 정밀한 표면비드 형상을 예측하고자 하였다.

Figure 3

Main effects on top-bead width

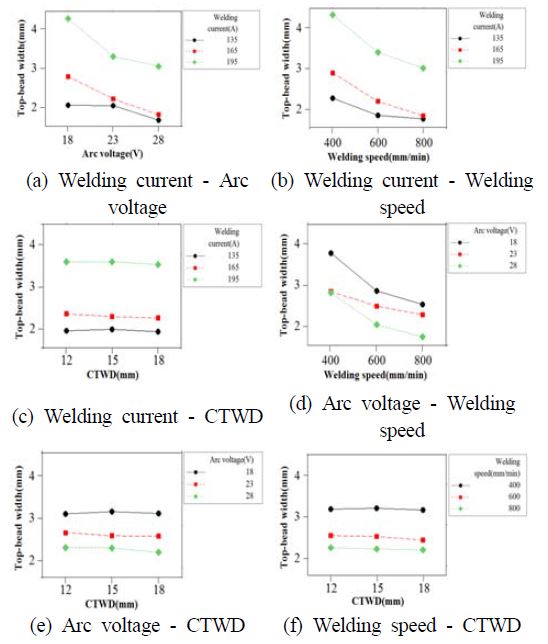
표면비드 폭에 따라 용접공정 변수(용접전류, 아크전압, 용접속도, 전극간 거리)간의 상호작용을 분석하고자 Figure 4에 상호효과를 나타내었다. 상호효과를 분석한 결과, Figure 4 (a)에 나타낸 바와 같이 아크전압이 높을수록 작은 표면비드 폭이 형성됨을 확인할 수 있었으며, 용접전류가 높을수록 큰 표면비드 폭이 형성되었다. 주요인 분석에서 용접전류의 영향력이 아크전압 보다 미비하기 때문에 전반적으로 표면비드 폭이 감소되는 것으로 사료된다. 또한 Figure 4 (d)에 나타낸 바와 같이 아크전압과 용접속도가 증가할수록 주요인 분석과 동일하게 표면비드 폭이 감소되는 경향을 확인하였다. 마지막으로 Figure 4 (c), Figure 4 (e), Figure 4 (f)에 나타낸 바와 같이 전극간 거리인 CTWD는 나머지 3개의 변수(용접전류, 아크전압, 용접속도)와 상호작용에서 표면비드 폭의 변화가 미비하게 발생되지만 큰 변화는 확인되지 않아 최적의 공정변수 선정에 적절치 못한 주요인자로 사료된다.

Figure 4

Interaction on top-bead width

2.3 용접부 기계적 특성의 영향

산업구조물 문자마킹 GMA 용접실험 결과 모든 실험조건에서 매우 안정적인 표면비드가 형성됨을 확인하였으며, 일부 고전압의 용접조건에서 약간의 언더컷(Undercut)이 발생되었으나 용접성에 영향은 미비한 것으로 확인하였다. 또한, 용접조건에 따라 용융부의 형상에 미치는 영향을 판별하기 위해 단면형상(Macro)을 촬영하여 용접부 특성을 분석하였다. 용접부의 표면비드 형상을 측정하기 위하여 용접이 완료된 시험편의 가로축 중간부분을 레이저절단기(Laser cutting machine)를 사용하여 40×20 mm의 크기로 절단하고 단면부를 연삭한 후 폴리싱(Polishing)을 수행하였다.

시험편의 단면비드형상을 잘 나타내기 위하여 질산, 염산, 알코올을 각각 1:3:1의 비율로 혼합하여 단면부에 대해 에칭(Etching) 작업을 수행한 후 정확한 표면비드 크기 측정을 위하여 광학 현미경 시스템을 이용하였으며, 총 81회의 실험조건의 단면 비드크기를 측정하였다. Figure 5는 표면비드 형상 측정에 사용된 현미경과 대표적인 단면 비드형상의 크기를 측정하는 화면을 나타낸다.

Figure 5

Measurement of bead geometry

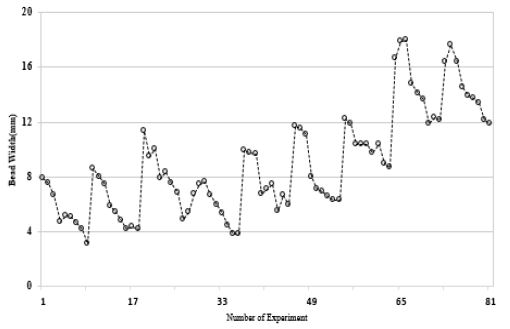
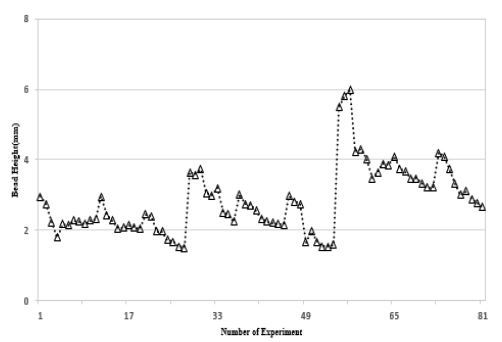
실험은 총 81개의 용접조건별로 각 3회씩 반복하여 총 243회 실시하였고 각 실험 후 냉각시간을 충분히 주고 예열에 의한 변형 및 시험 오류는 제거되었다. Figure 6 ~ Figure 7는 용접조건별 3회의 평균을 구하여 비드폭과 높이값을 나타내었다. 실험결과 슬래그 혼입(Slag inclusions), 용입불량(Incomplete fusion) 등의 용접결함이 없는 단면 비드형상임을 확인하였다.

Figure 6

Average of surface bead width

Figure 7

Average of surface bead height

3.1 문자마킹 용접공정 2차 회귀 예측모델 개발

반응표면분석법은 여러 개의 입력변수 x₁, x₂, x₃, ⋯, x_k가 복합적인 작용을 함으로써 출력변수 y에 영향을 주고 있을 때 이러한 반응의 변화가 이루는 반응표면에 대한 통계적인 분석방법이다. 이는 입력변수들과 출력변수 간의 함수관계를 데이터로부터 추정하여 입력변수들의 값의 변화에 따라 출력변수의 값이 어떻게 달라지는가를 예측하고 입력변수의 어떠한 값에서 반응량이 최적화가 되는지를 찾을 수 있는 것을 말한다. 그러므로, 가장 적은 수의 실험으로 좋은 정도를 주는 실험계획법이 무엇인가를 연구하고, 데이터분석을 통하여 추정되는 적합한 반응표면의 통계적인 성질을 규명할 수 있는 장점을 가지고 있다.

입력변수 x₁,x₂,x₃,⋯x_k와 출력변수 y간의 함수관계는 식 (2)로 나타내며, 선형 및 비선형 모델의 예측능력을 고려하였을 때 출력변수인 표면비드 폭과 높이의 예측값이 입력변수와 선형적인 관계를 갖는다고 가정했을 경우 이를 2차 선형회귀모델(Second order regression model)로 표현하면 식 (3)과 같다. I 는 용접전류(A), V는 아크전압(V), S는 용접속도(mm/min)를 나타낸다.

식 (3)은 최소제곱법(Method of least squares)에 의해 식 (4)와 같이 정리할 수 있다.

본 연구에서는 입력변수의 수가 3개 즉, k=3이므로 식 (4)는 식 (5)와 같이 확장할 수 있다.

여기서,$$ \widehat{y}$$는 표면비드 폭과 높이의 추정량이고, x_i는 입력변수(용접전류, 아크전압, 용접속도)들의 Coded unit이며, $$ \widehat{{\beta }_0}$$, $$ \widehat{{\beta }_i}$$, $$ \widehat{{\beta }_{ij}}$$ 는 각각 β₀, β_i, β_ij의 최소 제곱추정량을, ε은 오차를 나타낸다.

위 회귀모델(Regression model) 식 (5)을 구하기 위해서는 많은 실험을 통해 관련 데이터를 얻어야한다. 이와 같이 실험을 통해 관련 데이터를 얻으려고 한다면, 수많은 실험의 시행착오와 경제적인 손실이 발생할 수 있으므로 이러한 손실을 줄이고자 2차 회귀모델을 잘 반영하는 실험계획법의 반응표면분석법 중 완전요인설계를 적용하였으며, 각 항의 계수는 MINITAB을 이용하여 계산하였다. 회귀계수와 식 (5)를 사용하여 표면비드 폭과 높이에 대해 개발된 2차 회귀모델은 식 (6) ~ 식 (7)과 같이 나타낼 수 있다.

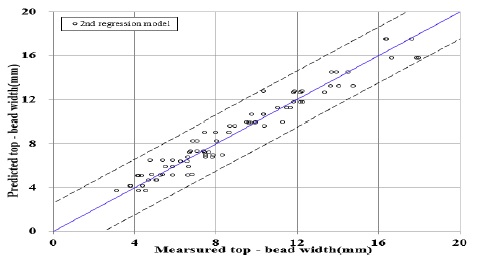
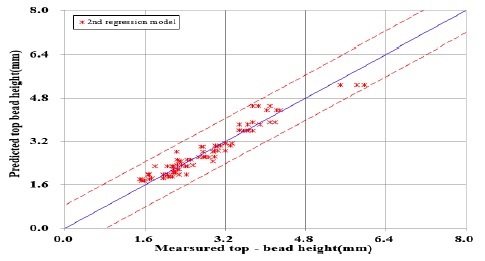
개발된 2차 회귀모델의 예측능력 확인을 위해 각 실험조건별 측정된 표면비드 폭과 높이의 측정평균값과 예측된 표면비드 폭과 높이를 비교하여 오차 범위를 나타낸 그래프는 Figure 8 ~ Figure 9와 같으며, 오차값의 범위는 대체로 신뢰할만한 결과를 나타냄을 알 수 있다.

Figure 8

Comparisons between measured and predicted top-bead width from the developed 2nd regression model

Figure 9

Comparisons between measured and predicted top-bead height from the developed 2nd regression model

Table 4는 개발된 모델의 분산분석 결과를 나타낸다. 결과를 보면 94.9 %, 91.5 %의 높은 결정계수 값을 가지고 있음을 확인할 수 있다. 이는, 표면비드 폭과 높이 총 변동의 95.2 %, 92.5 %가 개발된 회귀모델에 의해 예측이 가능함을 나타낸다. 즉, 회귀모델에 영향을 미치는 입력변수들의 독립적 영향뿐만 아니라 교호(Interaction)를 동시에 고려해야 함을 의미한다.

Table 4

Analysis variance tests for 2nd regression model

3.2 PSO를 이용한 문자마킹 용접공정 분석

PSO 알고리즘은 진화 연산처럼 방대하고 복잡한 함수에 대하여 전역적인 최적화(Global optimization)를 할 수 있는 장점이 있다. 이는 진화 연산보다 수행속도가 빠르고 알고리즘이 단순하여 대량의 메모리가 필요 없으며, 연속성과 비연속성의 양쪽에 적용이 가능하기 때문에 최근 크게 주목받고 있다. 본 연구에서는 PSO를 이용하여 문자마킹 용접 공정변수를 탐색하는 방법을 선정하고자 하였으며, 탐색하는 과정에서 탐색 결과에 대한 적합한 제한조건이 필요한데 이를 식 (8)과 같이 나타내었다[14].

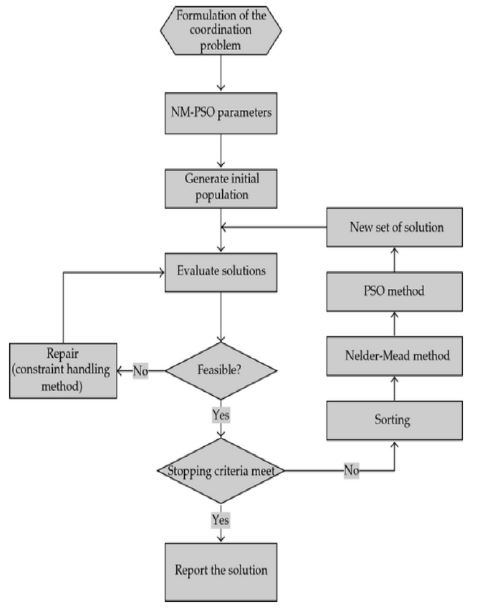
여기에서 위첨자 n은 반복계산의 순서를 나타내고, υ_id와 x_id는 각각 id번째 입자의 속도와 위치를 나타낸다. 그리고 c₁과 c₂는 상수로서 입자의 속도를 업데이트하는 정도를 결정하고, r₁과 r₂는 0과 1 사이의 값을 가지는 랜덤함수이다. 일반적으로 PSO 알고리즘의 수렴속도는 매우 빠른 것으로 알려져 있지만, 시간적인 변화가 포함되는 경우에는 경험에 근거하는 $$ p_{gd}^n$$와 $$ g_{gd}^n$$값의 의미가 변질될 수 있기 때문에 알고리즘이 수렴하지 못하고 무한루프에 빠질 수 있다[15]. 기본적으로 모든 탐색 알고리즘은 전역 최적해를 찾아내기 위해서 전역적 탐색과 국지적 탐색이 조화를 이루어야 한다. 이를 위해 PSO 기본 알고리즘에 관성가중치(Inertia weight)인 w를 추가하였으며, 전역 탐색과 국지탐색을 조화시키는 역할을 하며 시간의 선형 또는 비선형 함수를 사용하였다. 관성가중치를 너무 크게 설정하게 되면 지역해에 빠질 확률이 커지게 되고 너무 작게 설정하면 속도가 느려지게 되어 속응성을 떨어뜨리는 문제가 있다. 그러므로 본 연구에서는 초기에는 속응성을 높이기 위해서 관성가중치를 크게 주었다가 시간이 지남에 따라서 관성가중치를 줄여주는 방식이 일반적인 지역해에 빠지게 되는 것을 줄이고 또한 속응성을 높이는 것을 줄여가면서 최적해를 선정하였다. 이러한 관성가중치 w는 PSO의 기법에서 다양한 Swarm size로 정의가 가능하며, 다양한 사용자 변수제어를 바탕으로 PSO 최적화 기법의 프로그램 모식도를 Figure 10과 같이 구성하였다[16].

Figure 10

A flow chart for PSO method to predicting welding parameters

PSO 최적화 기법의 적용과 산출은 상용 수치해석 프로그램인 MATLAB을 이용하여 각각의 함수공차들을 적용하였으며, 총 81개의 조건에 대한 243개의 데이터를 이용하였다. 도출된 최적화 기법을 검증하기 위하여 3회 반복실험을 통한 평균 비드형상 데이터를 토대로 용접공정 변수를 산출하였다. 공정 변수는 용접전류 아크전압 용접속도의 범위인 최소 [135 A, 18 V, 400 mm/min]에서 최대 [195 A, 28 V, 800 mm/min]으로 선정하였으며, 지속적인 반복산출을 통해 공정변수 결과 오차를 감소시키다가 Swarm size의 감소수준인 속응성을 높여 최적해를 찾아가는 방법을 구현하였다. 목적함수에 사용된 변수들은 용접공정에서 주요인으로 판단되는 용접전류, 아크전압, 용접속도로 선정하고 이러한 변수에 의해 형성되는 표면비드 높이로 식 (7)을 입력하였으며, 제한함수는 표면비드 폭을 도출하는 식 (6)으로 선정하였다. 제한함수의 매개변수 상·하한값은 문자마킹에서 요구하는 표면비드 폭인 4 mm, 6 mm, 8 mm에서 ±0.5 mm씩 범위를 지정하였으며, 목적함수는 표면비드 높이를 적용하여 수요처에서 요구하는 3.5 mm를 준수하는지 확인하기 위하여 선정하였다. 최적화 기법의 적용성을 향상시키기 위해 함수공차를 다양하게 나누어 적용하였으며, PSO 최적화 기법의 변수들은 Table 5에 나타내었다. PSO기법에 의해 산출된 결과는 Table 6 ~ Table 8에 나타내었으며, 이를 토대로 문자마킹 용접부의 표면비드 폭에 대한 최적 공정변수를 확인하였다.

Table 5

PSO method parameters and their values

Table 6

The results of various swarm size using PSO method(4 mm)

Table 7

The results of various swarm size using PSO method(6 mm)

Table 8

The results of various swarm size using PSO method(8 mm)

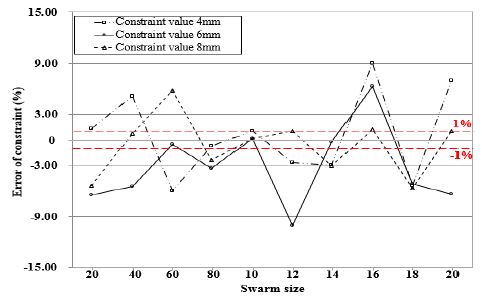
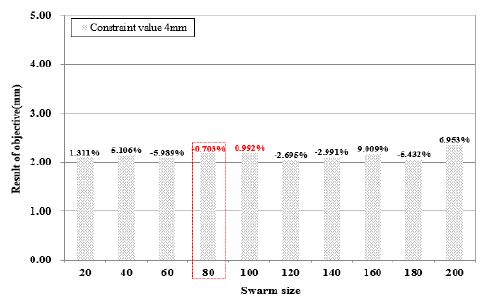
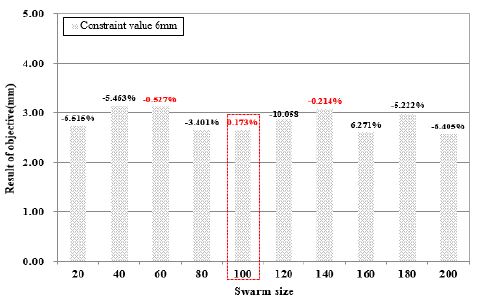
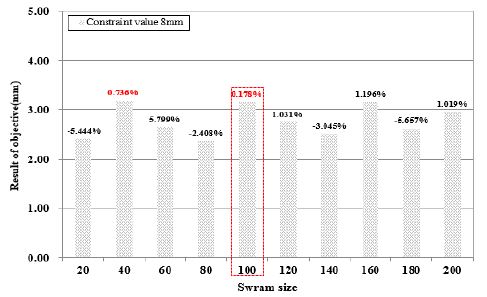
Figure 11은 PSO 기법을 적용하여 Swarm size에 따른 제한조건 오차율을 비교분석 하였으며, Figure 12 ~ Figure 14는 요구조건인 표면비드 폭(4 mm, 6 mm, 8 mm)에 따른 최적의 공정변수를 선정하였다. 각각의 용접부 표면비드 폭에 따라 산출된 용접공정변수를 기반으로 표면비드 폭 예측에 있어 1 %이내로 오차율을 나타내는 Swarm size 중 표면비드 높이가 가장 낮은 조건으로 채택하였다. 표면비드 높이가 높을수록 잔류응력이 과다해지는 현상이 발생되기 때문에 표면비드 높이가 낮은 조건이 내구성에 우수할 것으로 사료된다. 잔류응력은 취성, 파괴강도, 피로, 좌굴, 진동, 부식 등에 영향을 주는 중요한 요인이다. Figure 12에 나타낸 바와 같이 표면비드 폭이 4 mm일 경우 Swarm size가 80, 100일 때 1 %의 오차가 나타남을 확인하였으며, 그 중 80일 때 표면비드 높이가 2.176 mm로 가장 낮게 나타나 용접전류 149.66 A, 아크전압 19.02 V, 용접속도 714.65 mm/min으로 선정하였다. 위와 동일한 방법으로 Figure 13 ~ Figure14에서 표면비드 폭인 6 mm, 8 mm의 최적화된 용접 공정변수를 선정하였으며, 그 결과 표면비드 폭 6 mm의 경우 Swarm size가 100일 때 용접전류 169.40 A, 아크전압 19.66 V, 용접속도 668.15 mm/min로 선정하였다. 마지막으로 표면비드 폭 8 mm의 경우 Swarm size가 100일 때, 용접전류 185.67 A, 아크전압 19.21 V, 용접속도 794.66 mm/min으로 선정하였다.

Figure 11

The results for error of constraint according to swarm size

Figure 12

The results of objectives for 4mm top-bead width

Figure 13

The results of objectives for 6mm top-bead width

Figure 14

The results of objectives for 8mm top-bead width

3.3 문자마킹 용접부 3D Scan 분석

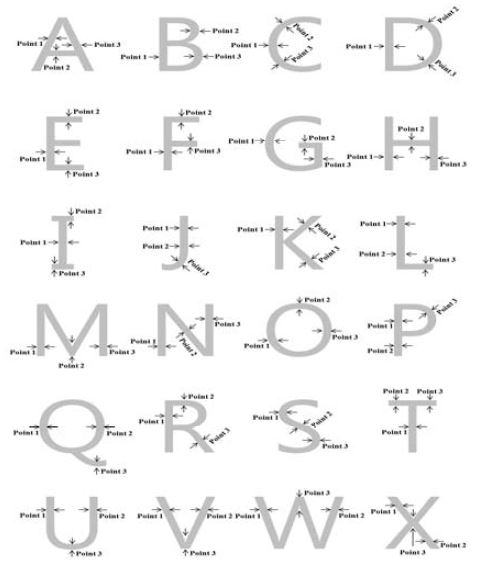
구축이 완료된 문자마킹 용접 공정변수에 대하여 문자마킹이 정상적으로 마킹이 되는지 확인하기 위해 본 검증실험을 수행하였으며, 용접실험을 위하여 조선해양 문자마킹 시스템을 사용하였다. 문자마킹 용접 공정변수의 검증은 용접이 완료된 각각의 시험편에 대하여 3D Scan결과로 확인하였으며, 본 검증실험의 실험계획은 A∼Z 26개 문자, 0∼9 10개를 포함해 36개의 문자로 선정하고 Figure 15에 나타낸 바와 같이 3개의 지점을 측정하여 요구하는 표면비드 폭이 도출되는지 확인하고자 하였다.

Figure 15

Measured positions for letter marking for verification of welding parameter

문자형태에 따라 1Bead에 대하여 총 36회의 실험을 수행하였으며, 위에서 선정한 용접 조건을 기준으로 용접실험을 수행하였다. 용접실험에 대한 공정변수의 검증은 표면비드 폭(4 mm, 6 mm, 8 mm)에 따른 치수오차가 ±0.5 mm 이내로 도출되는지 확인하였으며, 선정된 공정변수에 대하여 현장에 즉각 적용가능성을 확인하고자 하였다. 산업구조물 문자마킹에 대하여 선정된 표면비드 폭에 따른 용접 공정변수 검증실험 결과 다양한 문자 형태에 따라 만족할 만한 표면비드 폭이 도출되었다.

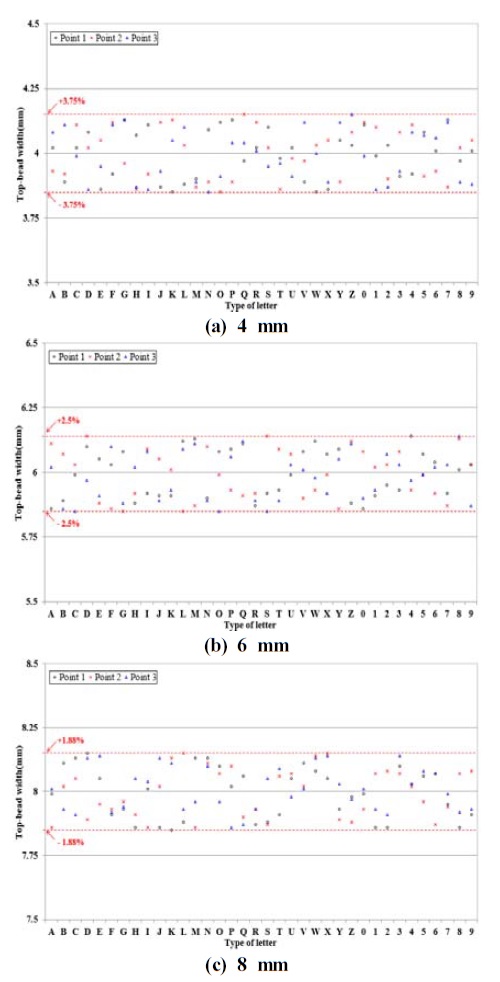
실험 결과 문자형태와 표면비드 폭에 따른 치수 오차는 최소 –0.15 mm에서 최대 +0.15 mm이내 임을 확인하였으며, 표면비드 폭 4 mm에서 최대 3.75 %의 오차율이 나타나고 6 mm에서는 최대오차 2.5 %, 8 mm에서는 최대오차 1.88 %가 확인되어 5 %이내의 오차율이 나타나는 매우 우수한 용접공정임을 확인하였다. 하지만 용착부 주변에 GMA 용접공정 특성상 발생되는 스패터는 몇몇의 문자들에서 발생되었으며, 이러한 스패터는 문자마킹 용접부 품질에 큰 영향은 미치지 않을 것으로 확인되고 용착불안에 의한 흄, 오버랩, 언더컷 등 용접부에서 발생될 수 있는 용접결함은 발생되지 않은 것을 확인하였다. Figure 16의 3D Scan 결과에 나타낸 바와 같이 동일한 용접 공정변수를 적용하여 용접을 수행했음에도 불구하고 다양한 표면비드 폭이 측정되었으며, 이는 용착부에서 용융상태에 있던 비드가 응고되면서 표면장력에 의해 미세한 변화가 발생되는 것으로 사료된다. 하지만 불균일한 표면비드 폭은 문자마킹을 요구하는 H중공업社에서도 0.5 mm정도의 오차를 허용하기 때문에 현장 적용성은 매우 우수한 것으로 사료된다.

Figure 16

Analysis for error of top-bead width according to type of letter