Adaptive Threshold Detection 기법을 이용한 수중 기동 표적의 거리 추정


Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
천해 및 심해에서 기동하는 수중무기체계에 대한 수중방사소음의 정량적 시험평가를 위해서는 측정 장비와 표적간 정확한 실시간 거리 추적이 필요하다. 거리 추적 기법으로 능동 및 수동 기법이 있으며, 본 논문에서는 고정밀 동기화된 송∙수신기 사이의 전송 시간차를 측정하는 단방향 ToA(Time of Arrival)기법을 적용한다. 이때, 도플러 필터 뱅크 방식보다 상대적으로 적은 계산량을 가지며, 이에 준하는 정확도를 가지는 ToA를 계산하기 위해 시간영역에서 CDS(Constant-Fraction Discriminator System)기반의 ATD(Adaptive Threshold Detection)기법과 주파수 영역에서 CZT(Chirp Z Transform)기반의 TD(Threshold Detection)기법 결과를 조합하였다. 제안된 기법의 성능 검증을 위해 수중실험을 진행 하였으며, GPS(Global Positioning System) 및 DFB(Doppler Filter Bank) 수중 추적기법과 비교분석 하였다.
Abstract
In underwater weapon systems, the accurate real-time distance tracking between the maneuvering target and measuring devices in shallow and deep waters is required for the quantitative test evaluation in underwater radiation noise. Passive and active SONAR systems exist as target recognition methods. In this study, ToA (time of arrival), which is one of the active SONAR systems, is applied to calculate the time difference between the transmitted and received signals accurately synchronized. To obtain the accurate ToA with minimum computation in comparison with the DFB (Doppler filter bank), we combine the result of the CDS (constant-fraction discriminator system) based on ATD (adaptive threshold detection) in the time domain and CZT (Chirp Z transform) based on TD (threshold detection) in the frequency domain. The validity of the proposed estimation scheme is confirmed by the underwater sea trial and analyzed using the GPS (global positioning system) and DFB tracking system.
Keywords:
One-way ToA (Time of arrival), ATD (Adaptive threshold detection), DFB (Doppler filter bank), Distance estimation키워드:
단방향 도래 시간, ATD (Adaptive Threshold Detection), DFB (Doppler Filter Bank), 거리 추정1. 서 론
수중무기체계 연구개발 과정에 있어서 수중방사소음 측정은 표적의 식별 자료로 이용될 뿐만 아니라 소음준위를 측정함으로써 표적의 작전수행 시 적 무기체계로부터 위험도 평가, 생존 기동 모드 선정 및 소음 감소를 위한 정비유지 기초자료로 활용된다[1]. 이러한 수중방사소음 준위를 산출함에 있어 소나 방정식에 근거해 음원과 수신단사이의 거리에 따른 전달 손실이 계산되어야 하고, 그에 따라 음원과 수신단사이의 실시간 거리 정보가 매우 중요하다.
수중에서 기동하는 표적 거리를 실시간으로 추적하기 위한 방법은 능동 및 수동 소나 기법이 존재하고 직관적이며, 구현이 간단한 능동 소나 기법 기반의 ToA((Time of Arrival) 방식이 많이 사용된다[2][3]. ToA 기법은 고정밀 동기화된 음원 및 수신기를 이용하여 송·수신기간 신호의 전송 시간차를 계산하는 기법이며, 이를 위해 상호상관관계 또는 경계선 검출 기법이 사용된다[4].
상호상관관계 기법은 매우 높은 ToA 정확도를 가지지만 직교성이 높으며, 잡음에 강인한 신호를 설계해야 하고 정확한 파형을 송신하기 위한 하드웨어를 구성함에 있어 어려움이 있다. 뿐만 아니라 표적이 수신기로 근접 기동하면 음원과 수신단의 상대속도로 인해 송신신호에 도플러 천이 현상이 발생하게 되고 복합 수중채널환경과 어우러져 상호상관관계 출력 에너지 값이 급격히 저하되는 문제가 발생한다[5][6]. 이를 극복하기 위해 모호 함수 기반의 DFB (Doppler Filter Bank)를 구성해야 하며, 연산과정에 있어 상당히 높은 계산량이 요구되므로 실시간 수중 표적 거리 추적기법으로 적합하지 않다[7].
경계선 검출 기법은 수신되는 신호가 특정 임계값 이상일 경우 신호의 위치를 결정하는 방법으로 적은 계산량을 가지며, 실시간 신호처리에 적합하다. 본 논문에서는 ToA 계산을 위해 경계선 검출 기법을 적용하였으며, 시간 및 주파수 영역의 ToA 결과를 종합 분석하여 정확도 향상을 도모하였다. 시간영역에서는 CDS(Constant-Fraction Discriminator System) 기반의 ATD(Adaptive Threshold Detection)기법을 적용하였으며, 주파수 영역에서는 시간-주파수 해상도를 높이기 위해 CZT (Chirp Z Transform) 적용 후 TD(Threshold Detection)를 계산하였다. 최종적으로 제안된 기법의 성능 검증을 위해 수중실험을 수행하였으며, GPS(Global Positioning System) 및 DFB 수중 추적기법과 비교 분석 하였다.
2. 제안된 수중표적 거리 추정 기법
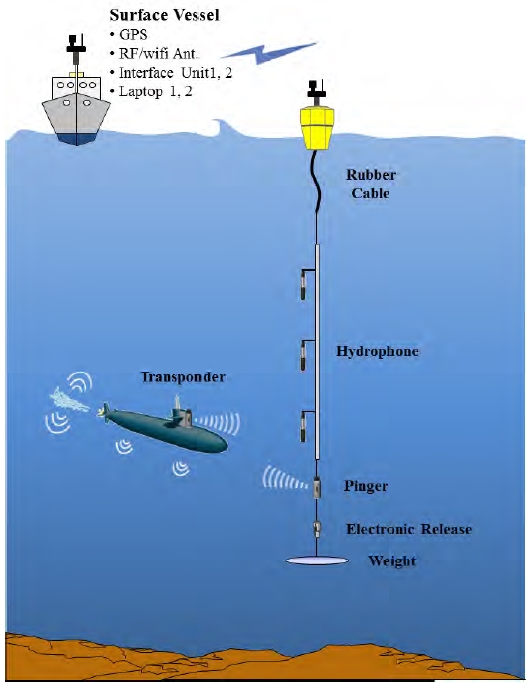
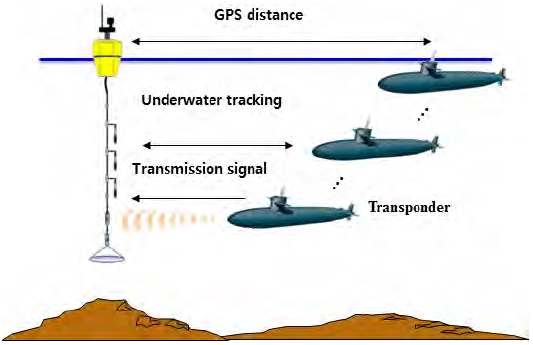
표적의 수중방사소음 측정을 위해서는 Figure 1과 같은 환경에서 실험이 수행된다.
시험선에서 측정 장비를 수중에 설치한 후 잠항 후 기동하는 수중 표적의 방사소음을 측정하며, 측정된 데이터는 시험선으로 WiFi 통신을 통해 전송한다. 이때, 측정된 방사소음의 준위를 계산하기 위해 식 (1)을 이용한다.
| (1) |
식 (1)에서 PL은 수신 신호를 FFT 후 계산된 스펙트럼레벨을 뜻하며, HS는 청음기 수신감도이고 Gain은 증폭도이다. TL은 전달손실량이며, 해상에서의 음파 전달은 여러 가지 요소에 의해 전달손실이 발생하지만 일반적으로 천해에서는 원통형 손실, 심해에서는 구형파 손실이 발생하며 거리의 함수로 근사화하여 식 (2)와 같이 적용한다[1].
| (2) |
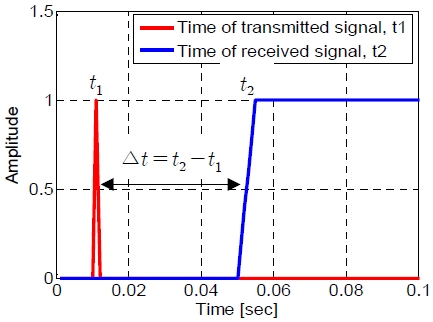
R은 표적과 측정 장비간 거리로써 Figure 2와 같은 단방향 ToA 기법으로 계산된다.
단방향 ToA 기법은 가장 간단하면서도 직관적인 방법으로 표적에서 수신기로 신호전송 시 전송거리는 시간에 비례한다는 특성을 이용한다. 신호를 보낸 시간이 t1, 수신 신호를 받은 시간을 t2라고 한다면 두 계측기의 거리는 식 (3)과 같다[8][9].
| (3) |
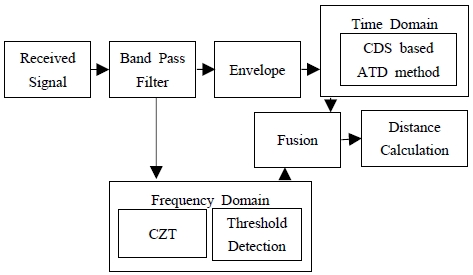
식 (3)에서 cd는 수심 평균 음속이며, t2를 계산하기 위해 Figure 3과 같이 시간영역과 주파수 영역에서 TD(Threshold Detection) 기법을 적용하였다.
2.1 시간영역에서의 CDS 기반 ATD 기법
Figure 1과 같이 표적이 계측기로 기동하여 CPA(Closet Point of Approach)를 통과하게 되면, 수신된 디지털 신호는 식 (4), 식 (5)와 같다.
| (4) |
| (5) |
A는 시간에 따른 표적 신호의 전달 에너지 E[n]의 변화 값이며, δ는 도플러, n0은 시간지연, VV는 표적의 진속도, θ는 표적으로부터 신호 입사각, g[n]은 배경소음을 나타낸다.
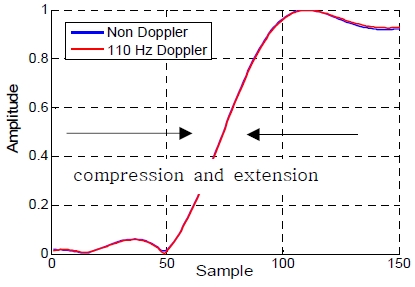
시간지연 n0를 계산하기 위해 경계선 검출 기법을 사용할 것이며, 이를 위해 A, δ, g[n]이 고려되어야 하나 표적의 CPA 및 θ에 따라 최대 110 Hz의 δ가 발생되더라도 Figure 4에서 확인할 수 있듯이 신호의 압축 및 팽창 값은 무시할 수 있는 수준이다. 따라서 도플러 값에 대한 신호의 시간 축 특성은 동일하다고 가정한 후 A 및 g[n]만 고려한다.
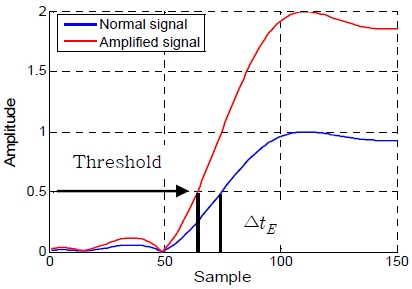
만약 동일 신호 수신시 해양환경에 의해 진폭 A가 2배 증가한다면, 임계값이 고정일 경우 Figure 6과 같이 시간오차 ∆tE가 발생되고 수신신호 A의 감쇄 및 증가 그리고 임계값이 커질수록 ∆tE값도 증가하게 된다[10].
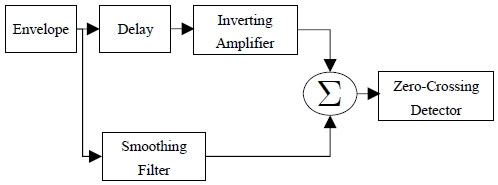
따라서, 진폭 A의 변화에 의한 신호 위치의 편차를 해결하기 위해 Figure 6과 같이 CDS 기반의 ATD 기법을 적용한다[10].
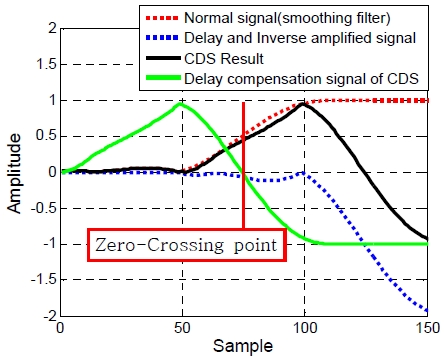
Figure 7은 CDS 기반의 ATD 기법을 적용한 결과이다. 수신된 신호에 smoothing filter 처리한 신호와 특정 지연 후 음수로 2배 증폭된 신호와의 연산을 수행하면 CDS Result와 같은 결과를 얻을 수 있다. 최종적으로 CDS Result에서 특정 지연을 보상하면 Delay compensation signal과 같은 결과를 얻을 수 있으며, Normal signal의 0.5 크기 지점에서 정확히 Zero-Crossing point 값을 얻는 것을 확인할 수 있다.
Figure 7의 결과로부터 진폭이 다른 유사 파형에 대해 CDS 기반의 ATD 기법을 적용할 경우 Figure 5의 결과와 달리 시간지연 값이 항상 동일한 지점에서 발생하게 된다. 하지만 배경소음 g[n]이 높아 SNR(signal to noise ratio)이 좋지 못하거나 다중경로 등에 신호가 오염될 경우 ATD 기법의 오차 확률이 높아져 이를 보완할 대책이 필요하다.
2.2 주파수영역에서의 CZT 기반 TD 기법
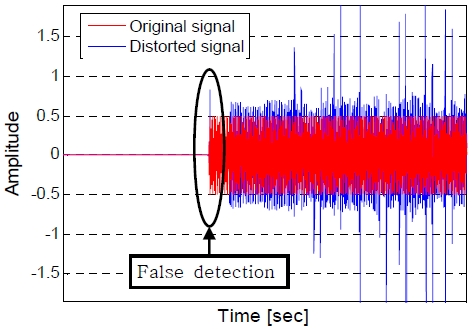
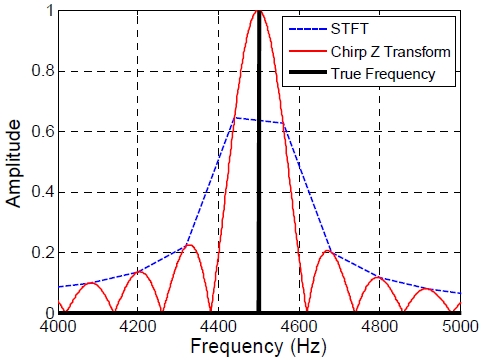
시간영역에서 수신된 신호가 다중경로 및 반향에 의해 왜곡될 경우 Figure 8과 같이 SNR이 좋지 못하게 되며, ATD 적용 시 표적 거리 오탐지 확률이 급격히 증가한다[9]. 따라서, 주파수 영역에서의 추가 분석이 필요하다. 주파수 영역에서 TD 정확도 향상을 위해서는 매우 짧은 시간영역에 대한 주파수 변환이 필요하다. 즉, 나이퀴스트 주파수 스펙트럼보다 좁은 주파수 대역 내의 신호에 대한 협대역 주파수 분석을 정밀하게 할 수 있어야 한다. STFT (Short Time Fourier Transform)기법은 매우 짧은 시간영역 신호에 zero-padding을 더하여 정밀하게 주파수 분석하는 방법이지만 연산량이 많다는 단점이 있다. 따라서 계산량이 STFT보다 월등이 낮고 성능이 높은 CZT(Chirp Z Transform)기법을 이용하여 주파수 분석하여 TD 시스템을 구현한다.
수신신호 x[n]에 대한 CZT 변환은 아래 식과 같다[11].
| (6) |
A는 주파수 단위원상의 시작위치, W는 등고선 상에서 점들 사이의비를 뜻하며, 식 (7)과 같다. 그리고 m은 주파수 영역의 변환 길이를 나타낸다.
| (7) |
위 식에서 f2-f1는 관찰하고자 하는 주파수 대역을 나타낸 것으로 분석 대역을 제한하기 때문에 식 (8)과 같이 주파수 해상도 ∆fCZT를 크게 상승시킬 수 있다.
| (8) |
식 (6)을 이용하여 특정 신호에 대한 CZT 분석을 한 결과 Figure 9와 같이 STFT보다 성능이 우수한 것을 알 수 있으며, 배경소음보다 3dB 높은 구간에 TD를 수행하여 ToA를 계산한다. 최종적으로 두 영역에서 계산된 ToA값에 Maximum Likelihood를 취하여 ∆t를 계산한 후 식 (3)을 이용하여 표적간 거리를 계산한다.
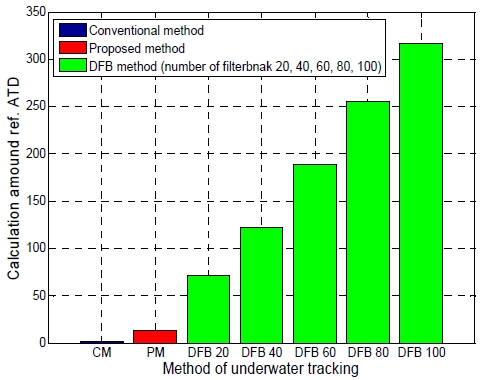
ATD 기법과 CZT 기법의 조합으로 구성한 제안된 기법의 실시간 처리 능력 확인을 위해 Table 1과 같이 신호 생성 후 동일조건에서 100번의 수중추적 연산한 결과 총 계산량은 0.19초로 확인되었다. 그리고 기존의 ATD 기법 및 DFB 기법과의 계산량 비교 결과는 Figure 10과 같다.
제안된 기법은 기존의 ATD 기법대비 약 13배의 계산량이 확인 되었고 모호함수 기반의 DFB 기법은 100개의 DFB 구성 시 기존의 기법대비 최대 24배의 계산량이 확인 되었다.
3. 해상실험 및 결과
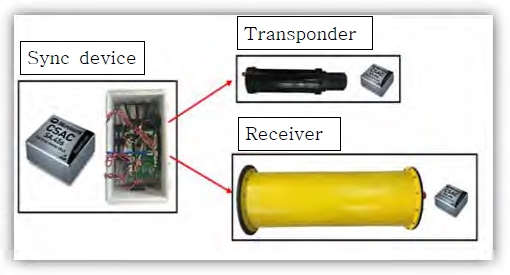
본 실험은 제안된 기법의 성능 확인을 위해 천해 및 심해 조건의 두 지역에서 실시되었다. 첫 번째 실험은 다중경로 환경에서 제안된 기법의 성능을 확인하기 위해 경상북도 문경시 경천호에서 Table 1과 같이 실시되었다. 실험장비 구성은 Figure 11과 같으며, 실험 시작 전 원자클럭 기반의 동기화 장치로 송신기 및 수신기를 정확하게 동기화 한 후 송신기는 로프로 고정하고 예인 보트 갑판에 매달아 일정한 속도로 기동하였다[6].
보트의 실제 기동 정보는 GPS를 이용하여 실시간으로 확인하였으며, DFB(Doppler Filter Bank)기반의 수중 추적기법과 제안된 기법의 수중추적 결과는 Figure 11과 같다.
Figure 12의 결과 값을 수치적으로 확인하기 위해 식 (9)를 이용하여 거리 상관계수를 계산하였으며, 두 입력 값의 공분산에 각 편차 값을 나눈 것과 동일하다[5].
| (9) |
위 식에서 E[∙]은 기댓값을 나타내고 dx,dy는 각 방법으로 추정된 거리 값을 나타낸다. 위 식에 GPS 데이터를 기준으로 2가지 값을 대입한 결과는 Table 2와 같으며, 3가지 방법의 거리 상관계수 및 CPA값의 차이는 거의 없다.
두 번째 실험은 심해 환경조건으로 동해 먼바다에서 Table 3과 같이 실시되었으며, 신호의 조건은 Table 1과 동일하다.
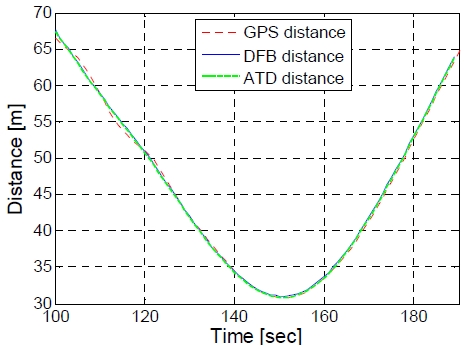
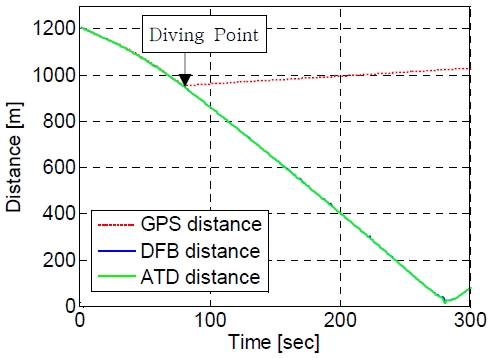
실험 당시 표적은 Figure 13과 같이 일정한 속력으로 기동 후 표적간 거리 약 950 m 지점에서 잠항하기 때문에 Figure 14의 GPS 추적 결과 값이 발산한다. 따라서, Table 4의 거리 상관계수 결과 값은 잠항전의 비교 값이고 CPA 값은 DFB 및 ATD 기법만 나타내었다. DFB 및 ATD 기법 비교결과 최대 거리 오차는 3 m 이내였으며, 거리 상관계수 및 CPA값의 차이는 미미한 것으로 분석되었다.
4. 결 론
본 논문은 천해 및 심해 환경에서 실시간으로 단방향 ToA 표적거리 추정을 계산하기 위해 직관적이면서도 간단한 경계선 검출 기법을 사용하였다. 일반적인 경계선 검출 기법은 시간영역에서 수신되는 신호가 특정 임계값 이상일 경우 신호의 위치를 결정하는 방법으로 적은 계산량 가지는 것이 특징이다. 하지만 수신되는 신호의 크기가 변동되고 다중경로 및 반향에 의해 신호가 오염될 경우 경계선 검출 기법 적용 시 거리 추정 오차가 발생된다. 이를 해결하기 위해 시간 및 주파수 영역에서 경계선 검출 기법을 적용하고 추정된 결과를 조합하여 거리 추정 오차를 최소화 하였다. 우선 시간영역에서 발생하는 신호 크기 변동에 따른 오차를 극복하기 위해 CDS 기반의 ATD 기법을 적용하였다. 그리고 다중경로 및 반향 등에 의한 오탐지를 최소화하기 위해 주파수 영역에서 배경소음보다 3dB 높은 지점에 대하여 경계선 검출 기법을 적용하였으며, 시간-주파수 해상도를 높이기 위해 CZT 기법을 적용하였다. 최종적으로 시간 및 주파수 영역에서 계산된 결과에 ML기법을 적용해 조합하여 표적거리 추정 하였다.
제안된 기법의 성능 검증을 위해 천해 및 심해에서 수중실험을 실시하였으며, 제안된 기법을 이용해 천해환경에서 수신된 신호에 대해 거리 추정한 결과 GPS 및 DFB 거리 추정기법과 비교해 최대 1.5 m 거리 추정 오차가 발생하였으며, 거리 상관계수 및 CPA 추적 성능의 차이는 미미하였다. 심해환경에서 실험 시 특정 구간에서 표적이 잠항하기 때문에 거리 상관계수 계산시 잠항 전 값을 적용하였으며, 제안된 기법은 GPS 및 DFB 거리 추정기법에 비해 최대 3 m 거리 추정 오차가 발생하였으며, 거리 상관계수 및 CPA 추적 성능의 차이는 미미하였다. 본 연구를 통해 수중 표적 거리를 실시간으로 추적할 경우 DFB 정확도에 준하는 ATD 기법 적용 및 활용 가능성을 제시하였다.
Acknowledgments
Author Contributions
The research presented in this paper wholly contributed by the author.
References
- J. Y. Choi, J. S. Ho, and P. H. Lee, “A calculation method of source level of underwater transient noise by frequency band”, Journal of the Korea Institute of Military Science and Technology, 13(4), p528-533, (2010), (in Korean).
- B. Friedlander, “A passive source location algorithm and its accuracy analysis”, IEEE Journal of Ocean Engineering, 12, p234-245, (1987).
-
K. W. Cheung, H. C. so, W. K. Ma, and Y. T. Chan, “Least squares algorithms for time- of-arrival based mobile location”, IEEE Transaction on Signal Processing, 52, p1121-1128, (2004).
[https://doi.org/10.1109/tsp.2004.823465]

- K. H. Lee, C. H. Yu, J. W. Choi, and Y. B. Seo, “ToA based sensor localization algorithm in underwater wireless sensor networks”, Journal of Institute of Control Robotics and System, 45(6), p641-648, (2009), (in Korean).
- M. S. Han, J. Y. Choi, D. S. Kang, K. Son, and P. H. Lee, “A study on optimal hydrophone arrangement for the direction finding of high speed moving traget in underwater”, Journal of the Korea Institute of Military Science and Technology, 20(3), p369-375, (2017), (in Korean).
-
M. S. Han, H. C. Lee, J. Y Choi, K. Son, and T. H. Kim, “Distance estimation method of underwater maneuvering target using ambiguity function in doppler shift environment”, Journal of the Korean Society of Marine Engineering, 42(4), p325-330, (2018), (in Korean).
[https://doi.org/10.5916/jkosme.2018.42.4.325]

- W. J. Park, K. M. Kim, M. S. Han, and J. Y. Choi, “Range estimation of underwater acoustic moving source using Doppler frequency map”, Journal of the Acoustical Society of Korea, 36(6), p413-418, (2017), (in Korean).
- M. S. Han, “Velocity and distance estimation of underwater fast moving target using doppler shift/TDoA (Time Difference of Arrival) Hybrid method”, Journal of the Korean Society of Marine Engineering, 41(9), p884-889, (2015), (in Korean).
- M. S. Han, J. Y. Choi, K. Son, and P. H. Lee, “Performance improvement of underwater target distance estimation using blind deconvolution and time of arrival method”, Journal of the Acoustical Society of Korea, 36(6), p378-386, (2017), (in Korean).
- J. W. Chang, and S. J. Lee, “Pulse position determination using adaptive threshold detector”, Journal of Advanced Navigation Technology, 21(2), p163-170, (2017), (in Korean).
- L. R. Rabiner, R. W. Schafer, and C. M. Rader, “The chirp z-transform algorithm”, IEEE Transaction on Audio and Electroacoustics, 17(2), p86-92, (1969).