기계학습 알고리즘을 활용한 베어링의 고장 예측 알고리즘 개발에 관한 연구
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
산업 현장에서의 기계 및 장비의 고장은 큰 인명피해 및 재산적 피해를 유발시키므로, 시스템의 상태를 실시간으로 파악하는 것이 매우 중요하다. 최근 4차 산업 혁명(Industry 4.0)으로 인해 기계 설비의 자동화/자율화를 위한 연구가 활발히 진행되고 있다. 특히, SVM(Support Vector Machine), RF(Random Forest) 알고리즘을 활용하여 기계 및 장비의 고장을 예측하고 대응할 수 있는 장비 예지보전 기술에 관해 많이 연구되고 있다. 본 논문에서는 기계학습(Machine learning; ML)을 이용한 베어링의 고장 예측에 관한 연구를 진행하였으며, DNN을 포함한 다양한 기계학습 알고리즘의 적용을 통하여 베어링의 고장 예측에 적합한 알고리즘에 대하여 기술하였다. 베어링의 고장 예측 알고리즘을 5단계(데이터 전처리, 특징 선택, 데이터 분할, 예측 모델 구성, 예측 모델 개선)로 나누어 설명한다. 본 논문의 결과를 활용하여 베어링의 고장 예측뿐만 아니라 다양한 기계 및 장비의 고장을 예측하는 문제에 적용할 수 있다. 또한, 본 논문의 결과를 활용하여 실시간 기계장비의 상태 모니터링 시스템 및 잔여수명 예측에 관한 연구로 확장해 나갈 것이다.
Abstract
Understanding the state of an industrial system in real time is critical because the failure of machines and equipment in the industrial field can cause great loss of life and property damage. Owing to the fourth industrial revolution (Industry 4.0), research on the automation and autonomization of machinery has been actively conducted. In particular, much research has been done on the technology of equipment maintenance and prediction, which can predict and cope with the failure of machines and equipment using support vector machine and random forest algorithms. In this study, we investigate the fault diagnosis of bearings using machine learning (ML). An algorithm suitable for predicting the failure of bearings is developed through the application of various ML algorithms, including deep neural networks. In this study, the fault diagnosis algorithm of the bearing is divided into five steps (data preprocessing, feature selection, data partitioning, configuring forecasting models, and improved forecasting model). The results of this study can be applied not only to the failure prediction of bearings but also to the problem of predicting the failure of various other machines and equipment. In addition, we will advance the research on condition monitoring systems and residual life prediction of real-time mechanical equipment using the results of this study.
Keywords:
Machine learning, Fault diagnosis, Condition monitoring, Predicting residual life키워드:
기계학습, 고장 예측, 상태 모니터링 시스템, 잔여수명 예측1. 서 론
4차 산업 혁명은 ‘3차 산업혁명을 기반으로 한 디지털과 바이오산업 등의 경계를 융합하는 기술혁명’을 의미하고, 이를 위해서는 빅 데이터, 사물인터넷, 인공지능, 클라우드 및 3D 프린팅 기술 등 다양한 기술이 요구된다. 특히, 제조 산업에서는 실시간으로 축적되고 있는 산업 현장의 기계/설비 운영 데이터를 이용하여 새로운 가치를 창출하고자하는 연구가 활발히 진행되고 있다[1]. 기계장비의 효율적인 관리 및 유지보수에 관한 연구가 진행됨에 따라 시스템의 고장에 대응하는 방법도 많이 변화되고 있다. 과거에는 기계 및 장비에 손상이나 고장이 발생되면 수리하는 사후정비(Corrective Maintenance)가 주를 이루고, 고가의 시스템만 예방정비(Preventive Maintenance)기술을 이용하였다. 하지만 최근 독일에서 ‘스마트 팩토리(Smart Factory)’에 대한 개념 및 제조 산업 분야의 생산성 향상에 대한 다양한 적용 사례들이 공유되면서[1][2], 기계 및 장비의 실시간 모니터링 및 실시간 상태기반정비의 중요성이 강조되고 있다. 실시간 모니터링 및 고장 예지 보전 기술의 개발을 위해서는 센서 및 스마트 디바이스를 활용한 데이터(빅 데이터) 수집, 빅 데이터 저장, 인공지능 기반 실시간 데이터 분석 및 시각화와 고성능의 컴퓨팅에 관한 연구가 필요하다. 최근에는 빅 데이터를 이용하여 기계장비의 고장을 사전에 예측하여 대형 사고를 줄이고, 수리비용의 절감을 위한 기계장비 고장 예지에 관한 많은 연구가 진행되고 있다[2][3].
특히, 베어링은 기계장비의 중요한 구성요소 중 하나로써 베어링의 이상 징후 예측에 관한 연구가 다양한 방법으로 진행되어 왔다. M. Y. Kim et al. [4] 는 저널베어링 로터시스템에서 획득된 데이터를 기반으로 진동 이미지를 구성한 뒤, 심층학습(Deep Learning; DL)을 통해 특징을 추출하고 고장을 예측하는 연구를 진행하였고, Y. S. Kim et al. [5]와 C. W. Lee et al. [6] 은지지 벡터 기계(Support Vector Machine; SVM) 알고리즘을 통해 결함을 분류하는 연구와 베어링의 정상과 이상을 진단하는 연구를 진행하였다. 최근에는 기존에 나타나지 않은 고장 패턴을 분석하여 유클리디안 거리를 이용한 실시간 학습 방법을 통해 고장을 진단하는 기법 에 관한 연구[7]를 포함하여 많은 연구들이 진행되고 있다.
본 논문은 다양한 기계학습 알고리즘을 베어링의 결함 분류문제에 적용하여 베어링의 고장 분류에 가장 적합한 모델을 구성하는 것으로써 베어링 결함 주파수 데이터를 사용하여 검증을 하였다. 구성된 고장 분류 알고리즘은 정확률(Accuracy), 오류율(Error rate), 특이도(Specificity), 민감도(Sensitivity), 정밀도(Precision) 및 재현율(Recall)의 기준을 바탕으로 최고의 성능을 내는 분류 모델을 선택한다.
2. 기계학습 알고리즘
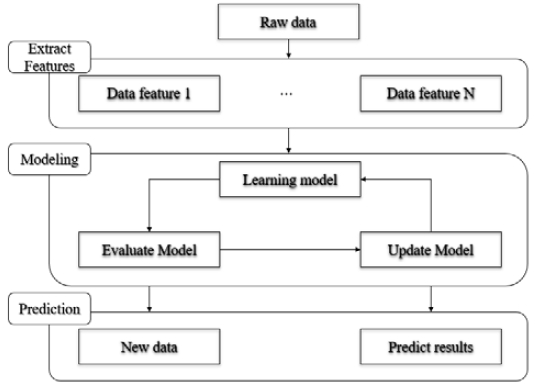
Figure 1은 기계학습의 작업흐름을 나타내며, 다섯 가지 주요 구성 요소(데이터 전처리, 모델 구축, 모델 평가, 모델 최적화 그리고 예측결과 평가)로 구별할 수 있다. 기계장비 고장 예측에 적합한 모델을 구성하기 위해서는 다섯 가지 주요 구성 요소별로 시행착오 과정을 거친다[8].
Machine learning work-flow
2.1 데이터 준비
기계학습 알고리즘은 학습 데이터를 사용하여 학습하고, 새로운 데이터(Test data)에 대하여 정확한 예측/분류를 위하여 모델을 개선해나가는 방법이다. 즉, 기계학습은 데이터를 활용하여 모델을 학습하는 기법으로, 기존에 수학/물리적으로 모델링이 불가능한 이미지 처리, 음성인식 등의 문제 해결에 적합하다.
기계학습 기반 모델의 예측/분류의 정확성은 데이터와 밀접한 관련이 있다. 구축된 예측/분류 모델에 사용된 학습 데이터가 새로운 데이터의 특성을 반영하지 못한 데이터로 학습이 이루어지면 어떠한 기계학습 알고리즘을 사용하여도 정확한 예측/분류가 어려워진다. 따라서 고품질의 데이터 준비가 정확한 예측/분류 모델을 생성하는데 중요한 역할을 한다.
2.2 기계학습 모델링
기계학습의 목적은 데이터 속에서 관계/패턴을 발견하여 새로운 입력에 대하여 결과를 예측/분류하는 것이다.
기계학습은 크게 지도학습, 비지도학습, 강화학습으로 나눌 수 있다. 본 논문과 관련된 지도학습 알고리즘들 중 대표적인 알고리즘은 의사결정나무(Decision Tree), 선형판별분석(Linear Discriminant), 로지스틱회귀(Logistic Regression), 지지 벡터 기계(Support Vector Machine), K-최근접 이웃(K-Nearest Neighbor), 앙상블(Ensemble) 그리고 심층 신경망(DNN)이다. 지면 관계상 이에 대한 보다 상세한 내용은 참고 문헌을 참조하기 바란다[9].
2.3 예측/분류 모델 평가
성능 측정은 예측 모델을 평가하는 데 사용되는 기계학습의 중요한 요소이다. 일반적으로 성능 측정을 위해서는 오차 행렬(Confusion Matrix)을 이용한다. Table 1은 오차 행렬을 이용한 분류성능 평가지표(Confusion matrix)를 나타낸다.
Confusion matrix for classification
오차 행렬에 나타난 각각의 기호에 대한 의미는 아래와 같다.
• True Positive(TP): 실제 True인 정답을 True라고 예측
• False Positive(FP): 실제 False인 정답을 True라고 예측
• False Negative(FN): 실제 True인 정답을 False라고 예측
• True Negative(TN): 실제 False인 정답을 False라고 예측
기계학습을 활용한 분류 문제의 평가 기준은 오차 행렬을 바탕으로 6가지의 방법이 있다[10]. 식 (1) ~ 식 (6)은 평가 기준에 대한 수식을 나타낸다. 이 과정(예측 모델 평가)의 목적은 분류하고자 하는 문제에 적합한 예측 모델로서 가능성 있는 후보 모델을 선정하는 것이다.
• Measure 1 – 정확률(Accuracy)
전체 관측치 중 실제 값과 예측치가 일치하는 정도를 의미(제대로 분류된 데이터의 비율)하며, 가장 직관적으로 모델의 성능을 나타낼 수 있는 평가 지표
| (1) |
• Measure 2 – 오류율(Error rate)
예측 모델이 제대로 예측하지 못한 관측치를 평가하는 지표
| (2) |
• Measure 3 – 특이도(Specificity)
실제 값이 Negative인 관측치 중 예측치가 적중한 정도를 평가하는 지표
| (3) |
• Measure 4 – 민감도(Sensitivity)
실제 값이 Positive인 관측치 중 예측치가 적중한 정도(Positive 값의 정확한 예측 정도)를 평가하는 지표
| (4) |
• Measure 5 – 정밀도(Precision)
Positive로 예측한 관측치 중 실제 값이 Positive인 정도를 나타내는 정확성(Exactness)을 평가하는 지표
| (5) |
• Measure 6 – 재현율(Recall)
실제 값이 Positive인 관측치 중 예측치가 적중한 정도를 나타내는 민감도(Sensitivity)와 동일한 평가 지표로 모형의 완전성(Completeness)를 평가하는 지표
| (6) |
2.4 예측 모델 성능 개선
예측 모델 평가로부터 분류 문제에 적합한 후보 예측 모델이 선별이 되고나면, 예측 모델의 성능 개선을 통하여 분류의 정확성을 향상시킨다. 그 방법은 아래와 같이 3가지로 분류할 수 있다[9].
• 모델 매개변수 조정(Tuning the model parameters)
기계학습알고리즘은 각 알고리즘(의사결정나무, Linear Discriminant, Logistic Regression, Support Vector Machine, K-Nearest Neighbor, Ensemble, DNN)에 대해 특정한 매개변수들로 구성이 되며, 이러한 매개변수들의 최적 값은 종종 데이터의 유형 및 구조에 따라 달라진다. 각 매개변수의 값 또는 여러 매개변수의 조합에 따라 모델의 성능에 영향을 미친다.
• 특성의 부차 집합을 선택(Selecting a subset of features)
주어진 데이터에는 많은 수의 특성이 포함되어 있다(다양한 특성이 예측 모델의 정확성에 영향을 미치는 경우가 존재). 따라서 예측 모델에 영향을 줄 수 있는 최소한의 특징으로 정확한 예측 모델의 구성이 필요하다.
• 데이터 전처리(Preprocessing the data)
데이터 전처리란 데이터에 포함된 불필요한 요소들(Noise)을 제거 또는 수정하여 데이터의 정확성을 높이는 것을 말한다. 기계학습에서 데이터는 모델 성능에 직접적인 영향을 미치므로 가장 중요하게 다루어지는 과정이다.
3. 분류 알고리즘을 활용한 베어링 고장 진단
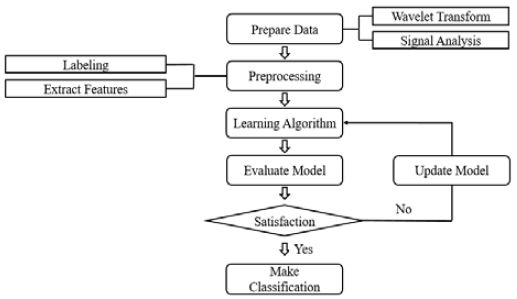
본 논문에서 2장(기계학습을 통한 기계장비 고장 예측 방법)에서 소개된 기계장비 고장 예측 방법을 활용하여 베어링의 결함 예측 문제에 적용하여 베어링 고장 예측에 가장 적합한 알고리즘을 제안한다. Figure 2은 베어링의 고장 분류에 가장 적합한 모델을 구성하는 과정을 보여준다.
A Flow-chart of constructing classification models
3.1 베어링 결함 주파수 데이터 및 신호 분석
기계학습(Machine learning; ML)에 대한 정의(“컴퓨터 프로그램이 작업 T에 대해 기준 P로 측정한 성능이 경험 E로 인해 향상되었다면, 프로그램은 작업 T에 대해 기준 P의 관점에서 경험 E로부터 학습했다라고 말할 수 있다[11].”)처럼 기계학습은 주어진 데이터를 학습시켜, 학습된 모델을 바탕으로 새로운 입력에 대한 결과를 예측 및 분류는 일련의 과정이다. 따라서 정확한 예측 및 분류를 위해서는 데이터의 준비과정이 중요하다. 본 논문의 데이터 준비 과정은 2단계(베어링 결함 주파수 데이터의 노이즈 제거 및 신호 분석)로 구성된다.
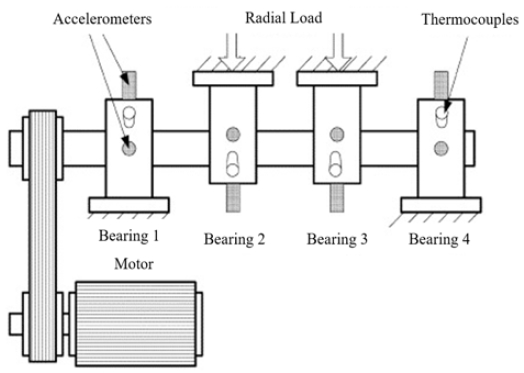
베어링의 고장 예측 모델을 구성을 위해 사용된 데이터는 연구용으로 공개된 IMS-Rexnord Bearing Data(https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/) 를 활용하였다[12]. IMS-Rexnord Bearing Data는 정상 신호와 고장 신호가 특정 시간 간격으로 기록되어있고, 샘플링 속도는 20 kHz이다. Figure 3는 베어링 테스트에 사용된 가속도계 센서와 베어링을 나타낸다. 샤프트에는 4개의 베어링이 설치되어있고, 베어링 당 2개의 가속도계 센서가 설치되어있으며, 회전 속도는 모터에 의해 2000RPM으로 유지되어 회전한다. 그리고 베어링과 샤프트에 6000lbs의 하중이 작용하고, 윤활유는 충분히 공급된다. 본 실험에 사용된 베어링의 설계 수명은 1억 번 이상 회전을 하였을 시 고장이 일어난다[12].
Bearing test rig and sensor placement illustration [12]
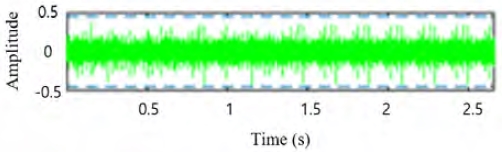
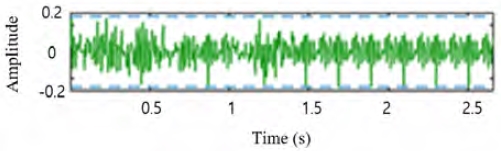
베어링 고장 예측 모델 생성을 위해서는 계측된 베어링 결함 주파수 데이터의 전처리 과정이 필요하다. 본 논문에서는 수집된 주파수 신호의 전처리(노이즈 제거)를 위하여 필터기반 웨이블릿 변환 기법(wavelet filter-based de-noising methods)을 사용하였다. 웨이블릿 변환 기법은 여러 연구 분야(자료압축, 신호 잡음제거, 영상처리 등)에서 다양하게로 적용되고 있다. 이 기법은 시간(또는 공간)과 주파수를 동시에 해석할 수 있다는 장점이 있다. 또한, 백색 소음 제거에 효과적이고, 신호 보존 능력이 좋은 것이 특징이다. 이 기법은 고주파장에서 시간 분해능과 저주파장의 주파수 분해능이 우수한 신호처리 기법이다[12]. 원본 주파수 데이터를 이용하여 주파수 영역의 신호 분석을 진행할 시 잡음으로 인해 정상 데이터를 결함 데이터로 잘못 판별할 수 있기에 필터기반 웨이블릿 변환을 사용하였다. Figure 4는 베어링 테스트에서 계측된 원본 주파수 데이터의 형상이고, Figure 5는 필터기반 웨이블릿 변환을 적용하여 신호 처리된 주파수 데이터(De-noise Data)의 형상을 보여준다.
Original data graph before wavelet transform
De-noise data using graph wavelet transform
3.2 데이터 전처리(Preprocessing the data)
본 논문의 목표는 지도학습(Supervised Learning) 방법을 바탕으로 베어링의 고장 예측 모델을 생성하는 것이다. 지도 학습은 라벨링 된 데이터를 활용하여 컴퓨터를 학습시키는 방법이다. 여기서, 라벨링 된 데이터란 입력 데이터에 대한 출력 데이터를 의미한다. 따라서 정확한 고장 예측 모델을 생성하기 위해서는 정확한 라벨링 된 데이터와 적절한 학습 알고리즘 선택이 중요한 요소이다.
기계학습 기반 베어링 고장 예측 모델을 생성하기 위해 데이터를 학습 데이터, 평가 데이터 및 예측 데이터로 분류한다. 본 논문에서는 라벨링 된 데이터의 70%를 학습 데이터로 사용하여 예측 모델을 생성하고, 나머지 30%의 데이터를 평가 데이터로 사용하여 생성된 모델의 예측 정확도를 평가하는데 사용하였다.
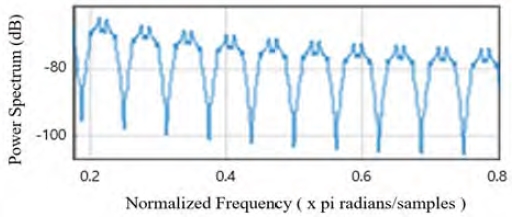
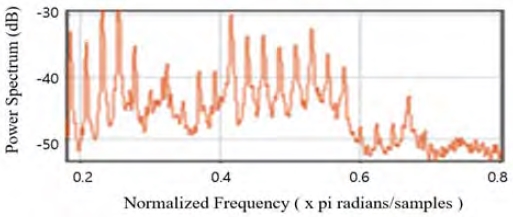
웨이블릿 변환 기법을 활용하여 전처리된(노이즈가 제거된) 데이터의 Power Spectrum의 결과(시각화된 데이터)를 활용하여 데이터의 라벨링 작업을 수행 하였다. Figure 6과 Figure 7은 정상 데이터의 스펙트럼과 결함 데이터의 스펙트럼의 일부를 보여준다. 정상 데이터의 스펙트럼은 규칙적인 형상을 보이고, 결함 데이터 스펙트럼은 불규칙적인 형상을 보인다.
Normal data signal spectrum – 2004.03.04. bearing B
Defect data signal spectrum – 2004.02.19. bearing A
특징 선택은 기초 입력 데이터를 수학적으로 변환하여 기계학습 모델에 사용할 새로운 특성을 만드는 과정을 의미한다. 이러한 특징 선택은 여러 종류의 측정된 데이터에 존재하는 중복성을 제거하여 기계학습 모델의 정확도와 계산의 효율성을 높일 수 있는 중요한 요소이다. Table 2는 본 논문에서 선택한 총 26가지의 특징을 나타낸다. 26가지의 특징은 요약 통계 영역의 유형인 평균, 중간 값, 표준편차, 평균 절대 편차, 1/4 분위 수, 3/4 분위 수, 왜도, 첨도를 사용하였고 주파수 영역의 유형인 우세 주파수, 스펙트럼 엔트로피, MFCC(Mel-Frequency Cepstral Coefficients)를 사용하였다.
Features selected for use in the classification models
3.3 학습 알고리즘
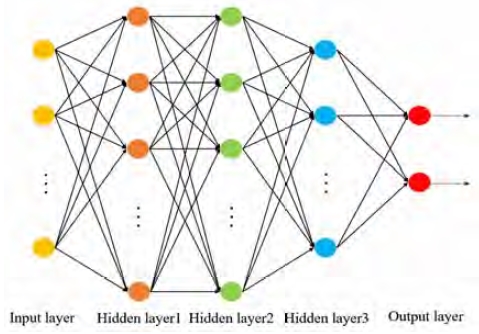
기계학습(지도학습) 알고리즘을 사용하여 베어링의 고장예측에 적합한 모델 생성을 시도하였다. 학습 알고리즘은 크게 7가지로 (의사결정나무, Linear Discriminant, Logistic Regression, Support Vector Machine, K-Nearest Neighbor, Ensemble, DNN) 분류하여 베어링 고장 예측에 적합한 알고리즘을 찾고자 시도하였다. Table 3은 각 알고리즘의 분류 방식에 따라 세부적으로 구별한 표이다. 여기서, DNN 모델의 구조는 Figure 8과 같고 , 이 구조를 바탕으로 활성화 함수에 따라 2가지(ReLU, Sigmoid)의 모델로 분류하였다.
Detailed algorithms used for classification models
DNN Model
모든 모델은 학습 데이터를 사용하여 학습하였다. 특히, 학습 데이터의 30%를 무작위로 평가 데이터로 분할하여 학습 모델의 정확도를 검증하였다.
3.4 예측 모델 평가
예측 모델 평가 과정은 평가 데이터를 이용하여 학습된 알고리즘 모델(3.3 학습 알고리즘)의 성능을 검증하는 과정이다. 본 논문에서는 예측 모델의 6가지 평가방법 중 4가지의 기준(정확률, 특이도, 민감도, 정밀도)으로 예측 모델을 평가하였다. 본 논문에서는 기계 고장의 분류 및 진단의 정확성이 중요(“고장을 고장으로 분류/진단”)하므로 4가지의 예측 모델 평가 방법 중 특이도를 가장 중요한 평가 기준으로 고려하였다. 아래 Table 4는 학습 알고리즘을 바탕으로 만들어진 예측 모델의 평가 결과(상위 5개 모델)를 보여준다.
Model evaluation results (Top5-specificity)
Table 4의 결과를 분석해 보면 활성화 함수 Sigmoid 와 ReLU를 사용한 DNN에서 과적합(overfitting) 문제가 발생한 것을 알 수 있다(특이도와 정밀도). 이 문제는 다음 장에서 소개될 ‘예측 모델의 성능 개선’ 방법으로 해결을 한다.
3.5 예측 모델의 성능 개선
주어진 문제에 적합한 예측 및 분류 알고리즘은 응용 분야와 데이터 종류에 따라 다르다. 따라서 최적의 모델을 찾기 위해서는 시행착오과정이 필요하다.
본 논문에서는 예측/분류 모델 생성 과정에서 발생할 수 있는 과적합 방지 및 예측/분류 모델의 성능 개선을 위하여 ‘특성의 부차 집합을 선택(Selecting a subset of features)’ 방법을 이용하여 예측 모델에 영향을 줄 수 있는 최소한의 특징을 추출하여 정확한 예측 모델을 구성하였다.
본 논문에서는 경사하강 최적기법(Gradient Descent Optimizer)을 사용하여 과적합을 방지하는 강력한 알고리즘인 NCA(Neighborhood Component Analysis)를 이용하여 특징 축소를 시도하였다(연관된 정도가 0인 특징 삭제).
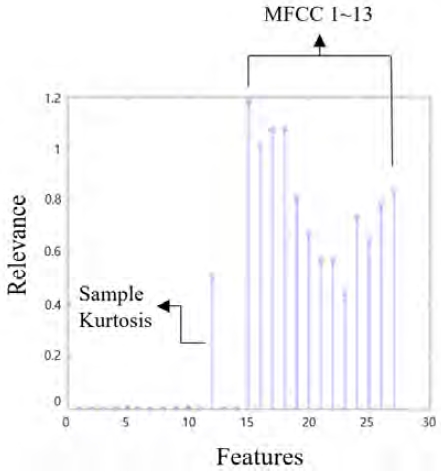
NCA는 분류 알고리즘 및 회귀 분석의 예측 정확도를 최대화시키는 특징들을 선택하기 위한 비모수적 방법이다[13]. 아래 Table 5는 초기에 사용한 특징 26가지 중 NCA 기반 특징 축소의 결과로 선택된 14가지의 특징을 나타낸다. Sample Kurtosis는 표본의 첨도로써 확률분포의 뾰족한 정도를 나타내는 척도이다. 즉, 관측치 들이 어느 정도 집중적으로 중심에 몰려 있는가를 측정할 때 사용되고, MFCC는 특정 값 스펙트럼 기반의 특징으로 비선형 주파수의 특성을 이용하는 방법이다[14].
Selected features using NCA
Figure 9는 26가지 특징과 ‘3.4 예측모델의 평가 과정’에서 사용된 모델들 간의 연관된 정도를 보여준다. 관련성이 높을수록 모델에 중요한 역할을 하고 있음을 의미한다.
Model relevance of features
본 논문의 목표인 최적의 베어링 고장 예측/분류모델을 선택하기 위해서 4가지의 예측 모델 평가 기준(정확률, 특이도, 민감도, 정밀도)중에서 음성(Negative)인 경우에 더 성능이 좋은 모델을 찾기 위해, 특이도를 가장 중요한 평가 기준으로 고려하여 최적의 예측/분류 모델로 선택하였다[15].
Table 6은 Neighbor Component Analysis를 이용하여 축소한 특징 데이터로 학습된 예측/분류기를 특이도 순으로 평가한 표이다. 그 결과, Table 4에서 나타났던 DNN 분류 모델의 과적합을 해결 할 수 있었고, Ensemble 분류 모델과 KNN 분류 모델은 특이도가 대부분 상승하였다. 하지만, Subspace KNN과 같이 일부 모델은 특징 연관도가 0인 데이터들이 사라지자 오히려 성능이 저하되는 결과를 보였다.
Prediction model results (Top5-specificity)
3.6 베어링 고장 예측/분류 모델 검증
성능 개선 과정을 통해 생성된 베어링 고장 예측/분류기를 시험 데이터를 이용하여 평가하였다.
Table 7은 시험 데이터를 이용한 평가에서, 예측 모델의 특이도를 가장 중요한 평가 기준으로 상위 5개 모델을 나타내었다.
Test model results (Top5-specificity)
3.7 결과 분석 및 고찰
기계의 고장 유무를 분류/진단에 있어서 적합한 모델(model)을 생성하기 위해서는 ‘신뢰성 있는 데이터 확보’와 ‘적절한 평가 기준’이 요구된다. 따라서 더 적합한 모델/분류 모델을 구성하기 위하여 정밀도와 재현율를 고려한 평가기준인 F1-score를 활용하였다(식 (7))[16].
| (7) |
Table 8은 식 (7)의 평가기준에 의한 상위 5개 모델의 결과를 보여 준다. 계산 과정에서 적용된 정확률 기반의 결과(Table 6, Table 7)과 동일하게 Fine KNN 모델과 Bagged Trees 모델이 가장 높은 F1 score를 가졌다.
Test model results (Top5–F1 score)
Table 6, Table 7 그리고 Table 8을 종합적으로 고려해보았을 때, 정오분류표를 기준으로 양성(Positive)인 경우를 분류할 때는 F1 score와 정확률이 높은 알고리즘인 Fine KNN과 Bagged Trees, 음성(Negative)인 경우를 분류할 때는 DNN Sigmoid 알고리즘을 사용하는 것이 좋다[15].
4. 결론 및 향후 연구
본 논문은 기계학습(Machine learning)을 이용하여 베어링 고장의 예측 및 진단에 관한 연구를 하였다. 연구의 결과를 살펴보면, 평가기준에 따라 우수한 예측/분류 모델이 다른 결과를 보인다.
• 정확률(Accuracy): Fine KNN 모델
• 특이도(Specificity): DNN Sigmoid 모델
• F1 score: Fine KNN 모델, Bagged Trees 모델
일반적으로 제조 산업에서 ‘정상상태를 고장상태로 오인’해서 드는 예방 정비 비용이 ‘고장상태를 정상상태로 오인’하여 고장이 발생했을 때 드는 후처리 비용보다 적다. 따라서 본 논문의 주제인 베어링 고장 예측 문제는 ‘정상 상태를 정상상태’로 진단하는 것도 중요하지만, ‘고장상태를 정상상태’로 오진단하여 발생되는 문제(위험성 및 경제성)도 중요한 고려사항 중 하나이다. 따라서 베어링 고장진단에 적합한 알고리즘을 선택하기 위해서는 특이도가 높은 DNN Sigmoid 알고리즘을 사용하는 것이 더 효과적이다.
하지만 공학에서는 주로 지지 벡터 기계, 의학에서는 의사결정나무, 그 외 분야에서도 지지 벡터 기계가 빈번하게 활용되고 있다[17]. 정확률이나 특이도 등의 평가 기준 외에도 알고리즘의 유의미성을 분석해서 기계 시스템에 적용하는 연구도 필요하다.
향후 실시간 학습을 통한 고장 예지에 대한 연구는 F1 score와 특이도, 정확률뿐만 아니라, 학습에 걸리는 시간도 평가 항목에 추가한 연구를 통해 새로운 데이터에 대한 실시간 학습(meta learning, online learning)과 고장 예지에 관한 연구를 진행하고 비지도 학습 분류 모델에도 적용하여 연구를 진행할 것이다.
Acknowledgments
본 연구는 2019년도 정부(미래창조과학부)의 재원으로 한국연구재단 (No. NRF-2017R1C1B5015989), 산업통상자원부와 한국산업기술진흥원이 지원하는 경제(광역)협력권사업 육성사업 (과제번호: P004736)과 산업통상자원부 ‘산업전문인력역량강화사업’ 의 재원으로 한국산업기술진흥원(KIAT)의 지원을 받아 수행된 연구(2019년 친환경ㆍ스마트 선박 R&D 전문인력 양성 사업, 과제번호: P0001968)의 결과입니다. 지원에 감사합니다.
Author Contributions
Conceptualization, J. H. Lee and J. C. Lee; Methodology, S. C. Shin; Software, J. H. Lee and D. H. Kang; Formal Analysis, J. H. Lee; Investigation, J. H. Lee; Writing—Original Draft Preparation, J. H. Lee; Writing—Review & Editing, J. C. Lee; Visualization, S. Y. Yoo and S. S. Lee; Supervision, J. C. Lee; Project Administration, J. C. Lee; Funding Acquisition, J. C. Lee.
References
- J. H. Cho, “[Issue focus] The Age of Industry 4.0 and speed”, Journal of Electrical World Monthly Magazine, 483, p16-19, (2017).
- S. W. Lee, “Intelligent failure prognosis and health management system technology for smart factory”, Journal of The Korean Society of Mechanical Engineers, 58(9), p32-36, (2018).
- J. H. Choi, “Introduction of failure prognosis and P.H.M”, Journal of The Korean Society of Mechanical Engineers, 53(7), p24-34, (2013).
- M. Y. Kim, J. H. Jung, J. U. Ko, and B. D. Yoon, “Health diagnosis method for journal bearing rotor systems using deep learning technique”, Abstracts of the KSNVE Annual Autumn Conference, p242, (2017), (in Korean).
-
Y. S. Kim, D. H. Lee, and D. W. Kim, “Fault severity diagnosis of ball bearing by support vector machine”, Transactions of the Korean Society of Mechanical Engineers B, 37(6), p551-558, (2013), (in Korean).
[https://doi.org/10.3795/ksme-b.2013.37.6.551]
- C. W. Lee, and B. H. Park, “A study on the optimal data learning for fault diagnosis of bearing”, Conference of The Korean Society of Mechanical Engineers, p1781-1783, (2017), (in Korean).
- Y. J. Cho, J. Y. Kim, and J. M. Kim, “Performance improvement of bearing fault diagnosis using a real-time training method”, Asia-pacific Journal of Multimedia Services Convergent with Art, Humanities, and Sociology, 7(4), p551-559, (2017).
- H. Brink, J. Richards, and M. Fetherolf, Real-World Machine Learning, Manning Publications, (2016).
- A. Geron, Hands-on Machine Learning with Scikit-Learn & TensorFlow, O’Reilly Media, (2017).
- S. Gollapudi, Practical Machine Learning, Packt Publishing, (2016).
- T. Mitchell, Machine Learning, McGraw-Hill Science/Engineering/Math, (1997).
-
H. Qiu, J. Lee, J. Lin, and G. Yu, “Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics”, Journal of Sound and Vibration, 289(4-5), p1066-1090, (2006).
[https://doi.org/10.1016/j.jsv.2005.03.007]
- J. Goldberger, S. Roweis, G. E. Hinton, and R. R. Salakhutdinov, “Neighbourhood components analysis”, In Advances in Neural Information Processing Systems, 17, p513-520, (2005).
-
J. E. Kim, and I. S. Lee, ”Speech/Mixed content signal classification based on GMM using MFCC”, Journal of The Institute of Electronics Engineers of Korea, 50(2), p185-192, (2013), (in Korean).
[https://doi.org/10.5573/ieek.2013.50.2.185]
-
M. Sokolova, N. Japkowicz, and S. Szpakowicz, “Beyond accuracy, F-score and ROC: A family of discriminant measures for performance evaluation”, Conference: Australasian Joint Conference on Artificial Intelligence, (2006).
[https://doi.org/10.1007/11941439_114]
- Y. Sasaki, The Truth of the F-measure, Teaching, School of Computer Science, University of Manchester, England, (2007).
-
H. H. Lee, S. H. Jung, and E. J. Choi, “A case study on machine learning applications and performance improvement in learning algorithm”, Journal of Digital Convergence, 14(2), p245-258, (2016), (in Korean).
[https://doi.org/10.14400/jdc.2016.14.2.245]