질량이 증가하는 회전형 역진자에 대한 저렴한 비용의 견고한 제어기 개발

2.1 역진자 시스템의 비선형 모델

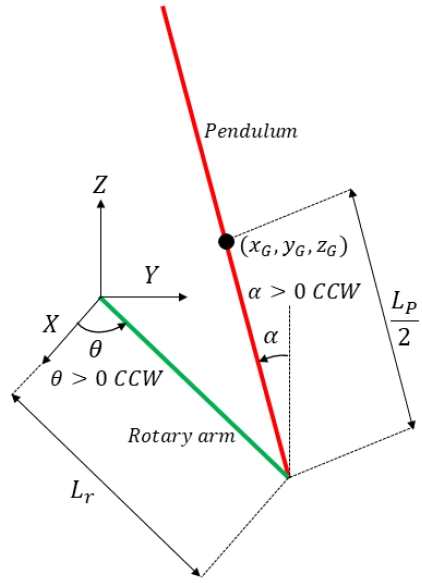
회전형 역진자 시스템은 Figure 1과 같이 진자와 암 그리고 암을 구동하는 모터로 구성되며, 암의 회전만으로 거꾸로 세워진 막대를 직립시키는 것이 그 목적이다. 이 시스템의 제어기를 설계하기 위해서는 역진자 시스템에 대한 수학적 모델링 하여 동작점 부근에서의 선형 모델을 선정하여 구해야 할 필요가 있다.

Figure 1:

Rotary inverted pendulum

본 절에서는 구동부를 포함한 역진자 시스템에 라그랑지안 동역학을 적용하여 비선형 모델을 구하고 이로부터 동작점 부근에서의 선형모델을 구한다[6].

Figure 2는 제어 대상으로 하는 역진자 시스템의 동역학적 직교 좌표계를 단순화하여 표현한 것이다. 진자의 평형점은 진자가 역으로 세워진 상태이며, 이때의 각도 α는 0°이다. 각도 α는 반시계 방향을 양의 각도로 한다. 각도 θ는 암의 각도를 나타내며 반시계 방향을 양의 각도로 한다.

Figure 2:

Rotary inverted pendulum conventions

진자의 질량을 m_p, 진자의 길이를 L_p, 질량중심에 대한 진자의 관성 모멘트를 J_p, 진자의 감쇠 계수를 B_p, 암의 길이를 L_r, 질량중심에 대한 암의 관성 모멘트를 J_r, 암의 감쇠 계수를 B_r로 나타낸다.

역진자 시스템의 수학적 모델을 유도하기 위해 역진자의 무게중심 좌표(x_G,y_G,z_G)를 구하면 다음과 같다.

무게중심의 속도 v_G를 좌표축 별로 구하고 진자의 위치 에너지는 E_pot를, 병진 운동과 회전 운동을 고려한 진자의 운동에너지를 E_kp로, 암의 회전 운동 에너지를 E_ka로 표현하여 역진자 시스템의 라그랑지안 L은 다음과 같은 식을 유도할 수 있다.

θ와 α에 대한 라그랑지안 방정식은 다음과 같은 관계가 성립한다.

τ는 구동 모터에서 역진자 시스템의 암으로 전달되는 토크이다.

다음으로는 암에 토크를 가하는 구동모터 계통의 수학적 모델을 구하도록 한다. 모터의 제어 입력 전압을 V_m, 전기자 권선의 저항을 R_m, 인덕턴스를 L_m이라 하면 전압 방정식은 다음과 같다.

여기서 전기자 권선의 인덕턴스는 극히 작으므로 무시하면 다음과 같다.

모터의 발생 토크는 전류 I_m에 비례하며 토크변환비율 k_t와 관계된다. 또한, 감속기어를 거치면서 k_g 비율만큼 회전속도가 변화하므로 다음과 같이 정리된다.

2.2 역진자 시스템의 선형 모델

역진자 시스템의 선형 모델을 구하기 위하여 역진자 시스템의 진자를 상향 수직(12시 방향)으로 세웠을 때를 평형점으로 간주한다. 평형점 근방에서 진자가 미소각도로 변화한다고 하면, α≈0, $$ \dot{\alpha }$$≈0, $$ \dot{\theta }$$≈0으로 가정하여 sinα≈α, cosα≈1, $$ \alpha \dot{\alpha }$$≈0으로 볼 수 있다.

이를 전개하여 $$ \ddot{\theta }$$와 $$ \ddot{\alpha }$$에 대하여 정리하면 다음과 같다.

2.3 역진자 시스템의 상태 및 출력 방정식

θ=x₁, α=x₂, $$ \dot{\theta }$$=x₃, $$ \dot{\alpha }$$=x₄, τ=u, 제어입력 u에 토크 및 입력전압 관계식인 τ를 대입하여 구동모터에 가해지는 입력전압 V_m에 대하여 정리를 한다. 그러면 구동모터에 가해지는 입력전압 V_m을 제어입력으로 하는 역진자 시스템의 상태 및 출력 방정식은 아래와 같다.

여기에 본 진자 시스템과 관련된 사양 Table 1의 값을 대입하면, 최종적으로 시스템행렬 A, 입력행렬 B, 출력행렬 C, 전송행렬 D는 다음과 같다.

Table 1:

Rotary pendulum system specifications

2.4 샘플링 타임을 고려한 역진자 시스템의 상태 방정식

연속 상태방정식 디지털 시스템인 ATmega128 16 [MHz] 마이크로 컨트롤러에 적용하기 위해서는 샘플링 타임(sampling time)을 고려하여야 한다. ATmega128을 이용한 제어기의 샘플링 타임은 인코더를 통하여 입력되는 외부 인터럽트의 발생 횟수에 따라서 차이가 발생한다. 그래서 12시 방향으로 역진자가 제어되는 가정하에서 시뮬레이션을 5차례 (50.35 [s], 50.20 [s], 51.02 [s], 51.44 [s], 51.64 [s])를 수행하여 10000회의 루프가 실행될 때의 시간을 측정한다.

평균 50.93 [s]/10000회로 샘플링 타임은 약 5.1 [ms]가 되어 T_s=0.0051 [s]로 설정한다.

3.1 스윙 업 제어기

역진자의 비선형 시스템을 12시 방향 부근에서 선형화하여 모델링 하였다. 이 모델링에 기반을 둔 제어기는 12시 부근에서만 유효하다. 초기 역진자 시스템의 진자는 중력에 의하여 아래로 처져 있다. 이 진자를 세우는 스윙 업(swing up) 제어가 필요하다[7][8].

역진자의 역학방정식은 다음 식 (14)와 같이 회전축 가속도의 관점에서 나타낼 수 있다.

여기서 전압 토크 관계식은 식 (14)에서 모터 효율 η_m과 기어의 효율 η_g를 고려하여 전압에 대하여 나타내면 다음 식 (15)와 같다.

3.2 상태피드백 제어기

역진자의 시스템 행렬 식에서 개루프 극점을 찾아보면 0, –32.48, -5.27, 7.39이다. 복소평면 우반면에 극점이 있으므로 시스템이 불안정함을 알 수 있다.

제어기의 감쇠비(damping ratio) ζ=0.6으로 설정한다. 감쇠비 ζ 값이 0.4 미만이면 큰 오버슈트가 발생하고, 0.8보다 크게 되면 시스템 응답이 느려지게 된다.

단위계단입력에 대한 출력이 목표값의 ±5%에 도달하는 정착시간 t_s를 1.25 [s] 이내로 하기 위한 비감쇠 고유진동주파수(undamped natural frequency) ω_n을 구한다. 감쇠비 ζ, 고유진동주파수 ω_n와 정착시간 t_s간의 관계를 나타내는 ω_n=4 [rad/s]이다. 설계 사양을 따르는 주요 지배극점(dominant pole)을 구해보면, p₁, p₂는 식 (16)과 같다.

여기서,

$$ \sigma =\zeta {\omega }_n=0.6\times 4=2.4$$와

$$ {\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}=5\sqrt{1-{0.6}^2}=3.2$$

나머지 비우세극점은 대표극점으로부터 충분히 떨어진 위치에 배치한다. 그러나 비우세극점이 허수축으로부터 너무 멀리 떨어져 있으면 큰 제어량이 요구되며 잡음 신호가 증폭될 수도 있다. 반대로 너무 가깝게 놓이면 기대한 성능을 얻기 힘들다. 그러므로 경험적으로 비우세극점의 고유진동수가 대표극점의 고유진동수의 3 ~ 5배 되도록 p₃, p₄를 -30, -40으로 설정한다.

A_d, B_d 및 희망 극점 값에 대하여 극점배치 기법을 적용하여 상태피드백 제어기 이득행렬 K_d를 구하면 다음과 같다[9].

위의 행렬 K_d의 각 요소는 상태 θ, α, $$ \dot{\theta }$$ 및 $$ \dot{\alpha }$$에 대응하는 제어 상수이다.

4.1 하드웨어 구성

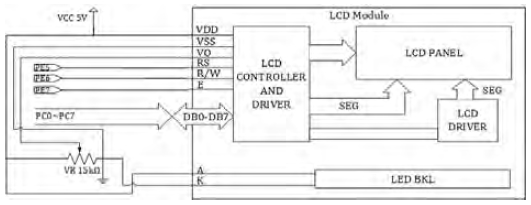
역진자와 제어기는 Figure 3과 같이 이루어져 있다. 그림의 상단부는 역진자 시스템의 구동부이고 하단부는 제어기이다. 이 제어기는 Figure 4와 같이 전원 공급부, 모터 구동부, 인코더 신호 수신부, 제어상태 표시부 및 ATmega128 메인 보드부로 구성되어 있다.

Figure 3:

Inverted pendulum and its controller

Figure 4:

Controller with ATmega128

4.1.2 인코더 신호 입력부

역진자의 회전각도와 암의 회전각도인 α, θ 값을 측정하기 위하여 싱글-엔디드(single ended) 광학축 인코더를 사용한다. 이 인코더는 1회전당 1024개의 펄스를 발생시키는 인크리멘탈 타입이다[11].

올바른 제어가 진행될 경우 대부분 12시 방향 0 [rad] 부근에서 정회전 또는 역회전 펄스 신호가 입력된다. 스윙 업 제어를 제외한 정상적인 역진자 제어는 ±15° 사이에서 이루어지게 되고 56개의 펄스 신호를 가지고 제어를 하게 된다.

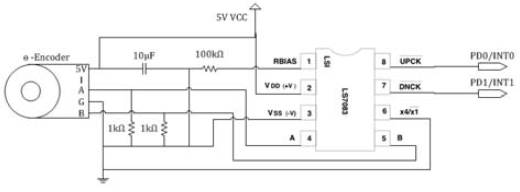
여기에서 α값으로 입력되는 인코더 펄스를 4체배 하기 위하여 LS7083 소자를 이용한다. Figure 5와 같이 LS7083 소자는 인코더에서 A채널과 B채널로 입력된 펄스 신호를 조합하여 4체배 된 다운클록 및 업클록 신호로 분리하여 출력한다[12]. 결과적으로 56개의 4배인 224개의 입력 신호로 역진자를 제어하게 됨으로써 보다 정밀한 제어가 가능하다. 인코더에서 입력되는 펄스 신호를 전압 변동에 의한 영향 없이 정확하게 입력받기 위하여 저항 1 [kΩ] 및 커패시터 10 [μF]를 이용하여 전기적 잡음을 필터링한다.

Figure 5:

θ angle signal encoder circuit for Theta variables

4.1.4 제어상태 표시부

역진자 제어기의 현재 상태를 나타내기 위하여 LCD를 사용한다. 진자가 12시 부근에서 제어가 이루어질 때 진자의 각도 α값, 암의 θ값, α의 각속도 $$ \dot{\alpha }$$값 및 θ의 각속도 $$ \dot{\theta }$$값을 표시한다. 그 이외에 역진자의 초기화 상태 및 스윙 업 상태를 표시한다. Figure 6와 같이 C 포트 C0~C7는 LCD 데이터 전송용으로 할당하고, E 포트 E5~E7은 LCD 제어 신호용으로 할당한다[13].

Figure 6:

LCD circuit

4.2 소프트웨어 구성

4.2.1 제어 순서도

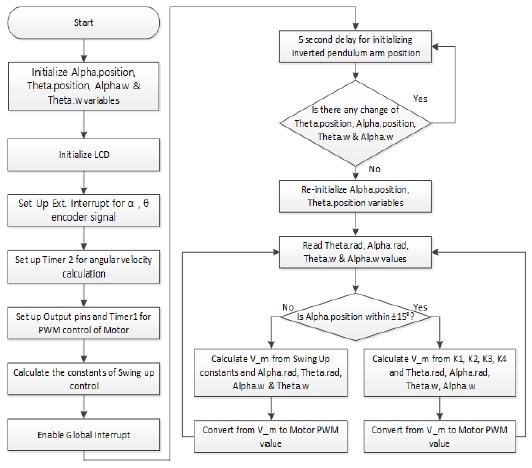
역진자 제어 시스템의 전체적인 제어 순서는 Figure 7과 같다. 시작 이후 각 변수 초기화 부분부터 전역인터럽트 활성화 부분까지는 ATmega128을 어떻게 사용할지 설정하는 처리 과정이다. 변수 Theta.rad, Alpha.rad, Theta.w 및 Alpha.w 값을 구하는 부분에서부터 주제어 루프가 시작된다. 주 제어루프는 스윙 업 루프와 역진자 제어 루프로 나누어진다.

Figure 6:

LCD circuit

4.2.2 좌표계

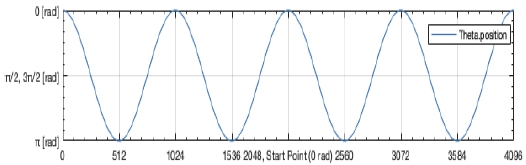
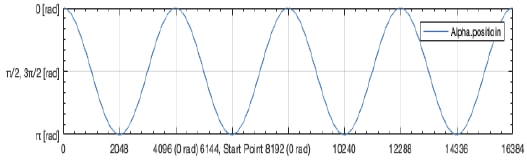
인코더로부터 입력되는 θ 및 α 각도 신호는 아래 Figure 8 및 Figure 9과 같이 표시할 수 있다. α 각은 인코더의 값이 0 ~ 16384의 값을 가지는 것으로 정한다. 한 바퀴가 1024 [pulse/turn]×4체배로 1바퀴 당 4096의 값을 가지게 되고 총 4바퀴의 값을 가질 수 있는 것으로 설정한다. θ값은 인코더 값이 0, 1024, 2048, 3072 및 4096 일 때 0 [rad]의 값을 가지고 α값은 0, 4096, 8192, 12288 및 16384일 때 0 [rad]의 값을 가진다. θ값의 시작점은 2048, 0 [rad]에서 시작을 한다. α각의 경우, 진자는 중력에 의해 6시 방향을 보고 있으므로 6144, 즉 π [rad]에 출발하는 것으로 설정한다.

Figure 8:

The value of Theta.position vs. actual θ angle

Figure 9:

The value of Alpha.position vs. actual α angle

4.2.5 모터 출력 제어

모터 출력 제어는 ATmega128의 16비트 타이머1(Timer1)과 비교출력장치를 이용한다. 타이머/카운터1 컨트롤 레지스터인 TCCR1A 및 TCCR1B를 이용하여 파형 발생 모드를 위상정정 PWM(Phase Correct Pulse Width Modulation) 모드로 설정한다[14].

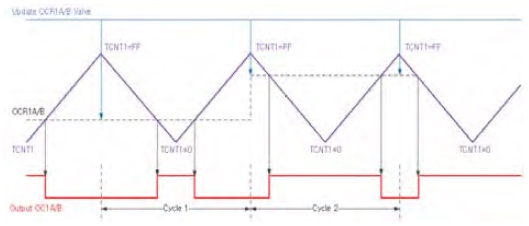
설정한 PWM 모드는 Figure 10와 같이 TCNT1 레지스터가 0부터 최댓값이 FF까지 1씩 증가하는 상승 경사와 FF값 이후에 다시 1씩 감소하는 하강 경사의 2중 경사 모양을 갖는다. 한 사이클의 주기는 TCNT1이 FF값부터 감소하여 0을 지나 다시 증가하여 FF-1값까지 총 2×FF회의 TCNT1에 대한 클록 펄스가 소요되며, 주기 계산은 아래와 같다.

Figure 10:

Phase correct PWM mode

$\[ \mathrm{P}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{P}\mathrm{W}\mathrm{M}\mathrm{C}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}=\frac{2\times \mathrm{\top }\times \mathrm{P}\mathrm{r}escale}{\text{CPUclock}} \]$

(18)

여기서 TOP는 최댓값 FF(16진수, 10진수로 255), 프리스케일은 256 그리고 CPU 클록은 16[MHz]이다. 따라서 PWM 파형 발생 주기는 8.16 [ms]가 된다.

위상정정 PWM 모드는 TCNT1 레지스터의 값과 OCR1 레지스터의 값을 비교하여 같아질 때, TCCR1A 레지스터의 COM1A1 및 COM1A0의 비트 설정에 따라 OC1A(PB5) 및 OC1B(PB6) 핀으로 출력된다.

역진자 시스템의 모터 정회전(암의 반시계방향)은 OC1B의 값을 0으로 설정하여 출력을 0 [V]로 하여 그라운드로 설정한다. 그리고 OC1A의 값을 조정하여 PWM 폭을 조정하여 모터에 인가되는 전압(+극)을 조정 한다. 역회전(암의 시계방향)은 OC1A와 OC1B의 설정을 반대로 사용한다.

모터 인가전압에 따른 OCR1A 및 OCR1B의 값 계산은 아래와 같다.

$\[ \text{OCAR1A/B=Motor Applied Voltage×}\frac{\text{256}\left(\text{0~FF}\right)}{\text{Moto}{\text{r}}^{\text{plied}}\text{Rated Voltage}} \]$

(19)

OCR1A 및 OCR1B의 값은 0 및 양의 정수 값을 가진다. 따라서 형변환 연산자 (unsigned char)를 이용하여 계산된 값을 형변환 한다.

4.2.7 상태피드백 제어기

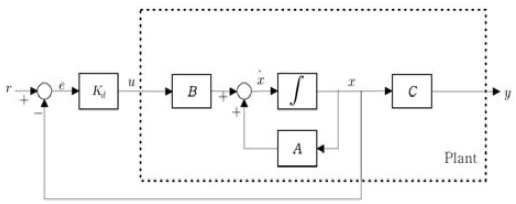
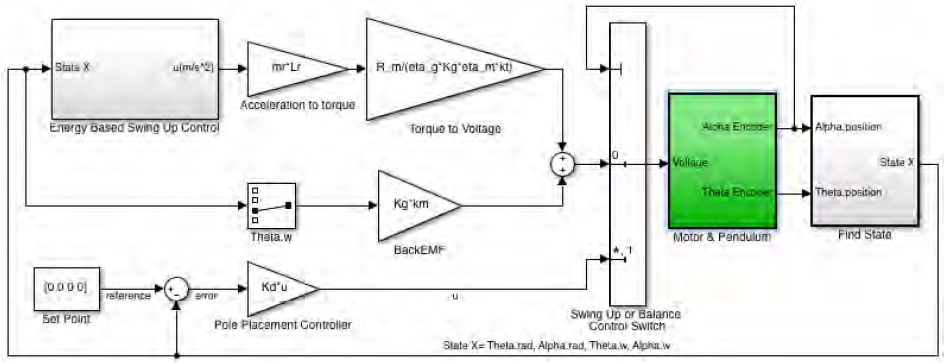
상태 피드백 제어기 K_d를 가지는 역진자 폐루프제어 시스템을 아래의 Figure 11과 같이 나타낼 수 있으며 사각 점선 내부는 역진자로 가정 할 수 있다[15][16].

Figure 11:

Closed loop control

기준값 r은 다음과 같다.

$\[ r=\left[\theta \alpha \dot{\theta }\dot{\alpha }\right]=\left[0 0 0\mathrm{ }0\right] \]$

(21)

전체제어 블록도는 Figure 12과 같으며 역진자 모터로 입력되는 전압 u는 식 (17)에서 구한 K_d 및 역진자 시스템의 상태변수 θ(Theta.rad변수), α(Alpha.rad변수) 및 그것의 각속도(Theta.w변수 및 Alpha.w 변수)의 곱으로 식 (22)와 같이 계산될 수 있다.

Figure 12:

Overall Control Diagram

$\[ u=\left[\theta \alpha \dot{\theta } \dot{\alpha }\right]{\left[K_1 K_2 K_3 K_4\right]}^T=K_1\theta +K_2\alpha +K_3\dot{\theta }+K_4\dot{\alpha } \]$

(22)

4.3 실험

역진자의 실험값은 Timer0을 이용하여 0.05 [s]의 간격으로 20 [s] 동안 SRAM에 인코더의 α, θ, 모터에 인가되는 전압 값을 저장한다. 실험 완료 후 UART를 이용한 시리얼 통신으로 하이퍼 터미널(Hyper terminal) 애플리케이션을 이용하여 각 데이터를 취득한다.

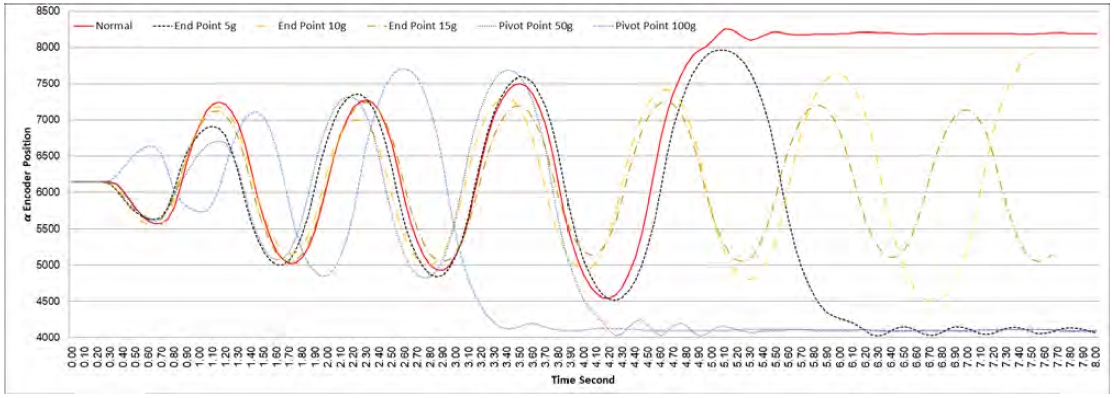
Figure 13의 Normal 그래프는 3장에서 모델링한 진자를 사용하여 구동 실험한 결과 그래프이다. 이 그래프와 같이 정상적으로 스윙 업을 구동을 하여 5.1 [s] 구간에서 역진자 제어가 시작되어 5.5 [s] 부근에서 α, θ 값이 0 [rad]으로 수렴한다.

Figure 13:

Test result for α-encoder positions

제어기의 강인성을 확인하기 위하여, 진자의 말단부에 각 5 [g], 10 [g] 및 15 [g]을 추가하여 질량 및 관성 모멘트의 변화를 준다.

Figure 13 중에서 5 [g]을 질량을 추가하였을 경우 6.25 [s] 부근에서 역진자 제어가 시작되어 진동을 3 [s] 동안 하였으나, 결국에는 α값이 0 [rad]으로 수렴하고 있다. 하지만, 10 [g] 및 15 [g]을 진자 말단부에 추가할 경우 Figure 13와 같이 진자가 스윙 업 단계를 넘어서지 못하고 계속 진동을 하는 결과를 보여 준다.

다음으로 진자의 축 부분에 가깝게 각 50 [g]과 100 [g]을 추가하는 방법으로 실험한다. 축 부분에 질량을 추가한 진자는 모델링한 진자만 사용했을 때보다 빨리 세워진다.

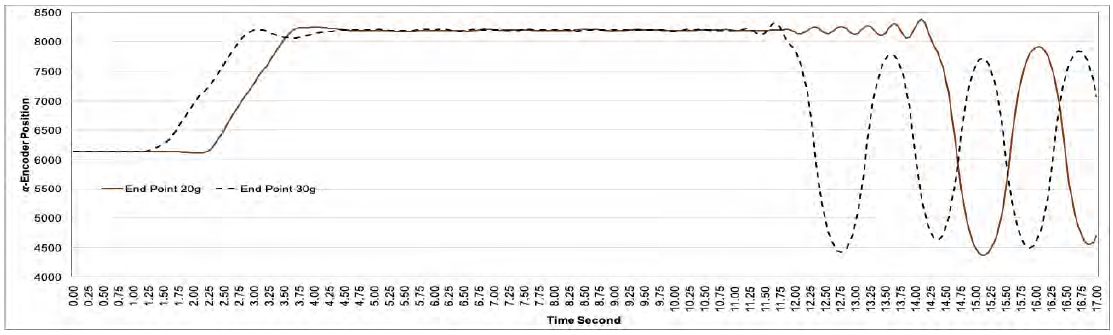
Figure 14과 같이 각 20 [g] 및 30 [g]를 진자 말단부에 추가하여 강제로 스윙 업 후, 각 12 [s] 및 11.25 [s] 부근에서 외부 충격을 가했을 경우, 진자는 중심을 잡지 못하고 쓰러진다. 20 [g]과 30 [g] 추가시, 20 [g]일 때가 30 [g]일 때보다 진동이 2 [s]정도 길게 발생하다가 넘어진다.

Figure 14:

Test result for α-encoder positions at forced inverted pendulum

또한, 진자 말단부에 10 [g] 추가할 경우와 마찬가지로 20 [g] 또는 30 [g] 추가 후 스윙 업 제어는 되지 않지만, 강제로 세우면 역진자 제어는 되는 것을 볼 수 있다.

앞의 실험 결과를 고찰해 보면, 진자의 질량 대비 3.9 [%]까지 진자 말단부 질량 증가에 대한 스윙 업 제어에 대한 강인성을 보인다. 그리고 23.6[%]까지의 진자 말단부 질량 증가에 대한 역진자 제어에 대해서도 강인성이 있는 것이 확인된다.

앞의 실험 결과를 고찰해 보면, 진자의 질량 대비 3.9 [%]까지 진자 말단부 질량 증가에 대한 스윙 업 제어에 대한 강인성을 보인다. 그리고 23.6[%]까지의 진자 말단부 질량 증가에 대한 역진자 제어에 대해서도 강인성이 있는 것이 확인된다.

Author Contributions

M. B. Sim; system modeling, T. Y. Jeon; coding, design & Writing-Original Draft Preparation, Y. C. Lee; Writing-Review & Editing, B. G. Jung; Supervision