채널 간극 및 개수에 따른 판형 응축기의 열전달면적 및 압력강하 분석
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
최근 화석연료의 대체방안으로 유기랭킨사이클을 이용한 발전기술이 주목받고 있다. 판형 열교환기를 사용하는 것은 유기랭킨사이클의 소형화에 있어 효과적이다. 판형 열교환기의 채널 간극과 채널 개수는 열전달면적 및 압력강하에 직접적인 영향을 미치는 변수이다. 압력강하는 사이클의 효율을 감소시키는 요소이므로 열역학적 사이클의 설계단계에서 정확하게 예측하는 것이 중요하다. 본 연구에서는 유기랭킨사이클용 판형 응축기에 대한 적합한 열전달 및 압력강하모델을 선정하고, 열전달 및 압력강하를 동시에 연산할 수 있는 알고리즘을 개발하였다. 개발된 알고리즘은 참고문헌의 연구결과를 기준으로 검증하였다. 검증결과는 개발된 알고리즘이 충분한 신뢰성을 갖는 것으로 나타내었다. 검증을 마친 알고리즘을 이용하여, Kim 등의 실험용 판형 응축기의 압력강하 개선을 위한 연구를 수행하였다. 그 결과, 채널 간극이 1.6mm 이상, 채널 개수가 93개 이상에서 응축기의 입구압력 대비 3% 이내의 압력강하를 기대할 수 있었다.
Abstract
Recently, power generation technology using an organic Rankine cycle has attracted attention as an alternative method of fossil fuels. Using a plate heat exchanger is effective at miniaturizing the organic Rankine cycle. The channel distance and number of channels in the plate heat exchanger are variables that directly affect the heat transfer area and pressure drop. Accurate prediction during the design step of the thermodynamic cycle is crucial because the pressure drop is a factor that reduces the efficiency of the cycle. In this study, suitable heat transfer and pressure drop models for a plate-type condenser of an organic Rankine cycle were selected and an algorithm was developed to simultaneously calculate heat transfer and pressure drop. The developed algorithm was verified based on the results of the reference literature. Verification results indicated that the developed algorithm has sufficient reliability. Using the validated algorithm, a study was then conducted to improve the pressure drop of an experimental plate-type condenser of Kim et al. Results revealed a pressure drop of less than 3% to the inlet pressure of the condenser could be expected when the channel distance was 1.6mm or more and the number of channels was 93 or more.
Keywords:
Plate-type condenser, Channel distance, Number of channels, Heat transfer area, Pressure drop키워드:
판형 응축기, 채널 간극, 채널 개수, 열전달면적, 압력강하1. 서 론
최근 산업에서 사용조건 및 목적에 따라 다양한 형식의 열교환기가 사용되고 있다. 판형 열교환기(PHE: Plate Heat Exchanger)는 고온유체와 저온유체가 번갈아 통로에 유입됨으로써 매우 효과적인 열전달을 기대할 수 있다[1]. 따라서 판형 열교환기는 열전달계수가 높으며, 각-관 열교환기와 비교하여 열전달면적이 작아 소형화가 가능하다[2].
판형 열교환기는 소형화의 장점으로 있으므로 중∙저온 열원을 다루며, 비교적 유체의 온도변화가 적은 유기랭킨사이클의 열교환기로 사용하기에 적합하다. T. W. Lim et al. [3]은 선박폐열회수용 유기랭킨사이클의 판형 열교환기에 관하여 연구를 수행하였다. 여기서, 다양한 문헌에서 제시하는 열전달모델에 관하여 비교분석하였다. 각 문헌의 모델은 동등한 열역학적 조건에서 서로 상이한 열전달계수 제시함에 따라 판형 열교환기의 해석에 있어 보다 적합한 해석모델을 선정하는 것이 중요하다.
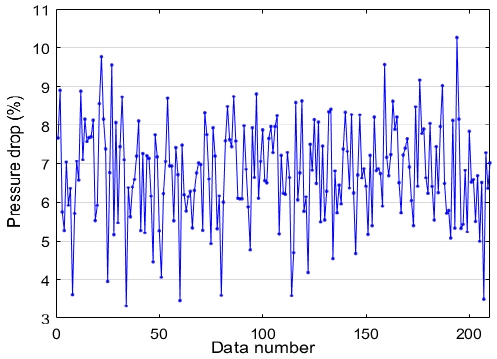
J. S. Kim et al. [4]은 반경류 터빈 및 판형 열교환기로 구성되는 유기랭킨사이클용 장비를 구축하여 실험을 수행하였다. Figure 1은 실험 시 판형 열교환기 형식인 판형 응축기의 입구압력대비 압력강하를 나타낸다. 여기서 압력강하가 약 3.31 ~ 10.27%에 달하였다. 열교환기 내 압력강하는 사이클의 비가역성을 초래하므로 열역학적 효율을 저하시키는 요소이다[5]. 따라서 열교환기 내 지나치게 큰 압력강하가 발생할 경우 적절한 판형 열교환기의 개선조치가 필요하다.
판형 열교환기는 채널 간극 및 개수를 조정함으로써 열교환기의 개선이 용이하다는 장점이 있다[2]. D. Hu et al. [6]은 판형 열교환기를 적용한 유기랭킨사이클의 예비설계 및 탈설계 성능분석을 수행하였다. D. Hu et al. [6]의 연구에서 채널 간극은 판형 열교환기의 열전달면적 및 압력강하에 지대한 영향을 미쳤다. 또한 채널 개수는 열전달면적을 결정하며, 이는 압력강하에 영향을 미치는 요소가 된다.
한편, 열교환기의 열전달 및 압력강하를 동시에 고려할 시 반복계산을 통한 설계지점을 모색해야 한다. 또한 작동유체의 상태가 변화하는 이상유동구간은 열교환기 해석에 있어 쉽지 않은 문제이다. 본 연구에서는 적합한 열전달 및 압력강하모델을 선정한 뒤, 모델의 검증을 수행하였다. 여기서, 열전달 및 압력강하를 동시에 연산이 가능하며, 이상유동구간을 세부구간으로 나누어 해석하도록 알고리즘을 프로그래밍 하였다. 검증을 마친 알고리즘을 통하여 채널 간극 및 개수에 따른 J. S. Kim et al. [4]의 실험용 판형 응축기의 열전달면적 및 압력강하를 분석하였다. 이를 통하여 상기 판형 응축기의 압력강하개선을 위한 채널 간극 및 개수를 제시하였다. 판형 열교환기의 분석을 위한 프로그래밍은 공학 수치해석 프로그램 MATLAB R2016a [7]를 이용하였다.
2. 판형 응축기의 해석모델
2.1 판형 열교환기 기하학적 구조
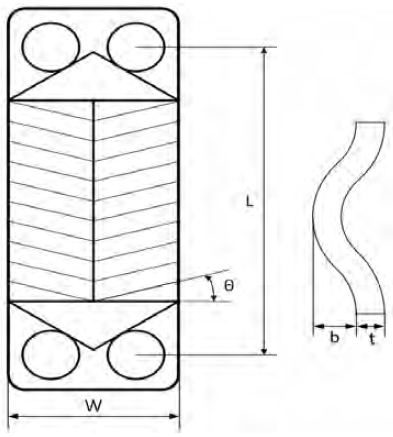
판형 열교환기의 기하학적 구조는 Figure 2와 같다. 이러한 판형 열교환기는 V자 모양으로 쉐브론각(θ)을 형성하는 헤링본 패턴을 지니고 있다[2]. 열전달 및 압력강하 해석에 필요한 수력직경(Dh)과 질량유속(G)은 각각 식 (1) ~ 식 (2)로 표현할 수 있다.
| (1) |
| (2) |
2.2 열전달면적 및 압력강하 산정
열교환기의 설계에 있어 해석모델은 해석결과에 지대한 영향을 미치므로, 많은 연구에서 실험을 통한 열전달 및 압력강하 상관식이 제시되었다. 본 연구에서는 유기랭킨사이클용 판형 응축기를 대상으로 해석한 D. Hu et al. [6]의 연구를 참조하였다.
열교환기의 총열전달계수(U), 대수평균온도차(∆Tlm) 및 열전달률()은 각각 식 (3), 식 (4) 및 식 (5)와 같이 정의된다. 그리고 이 값들을 이용하여 식 (6)과 같이 열교환기의 열전달면적(A)을 구할 수 있다. 또한 열교환기내의 압력강하(∆P)는 식 (7)을 통하여 산정한다. 여기서 열교환기 종류 및 유동상태에 따라 적절한 열전달계수(h) 및 마찰계수(f)를 선정하는 것이 중요하다.
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
3. 해석모델의 검증
3.1 해석 알고리즘
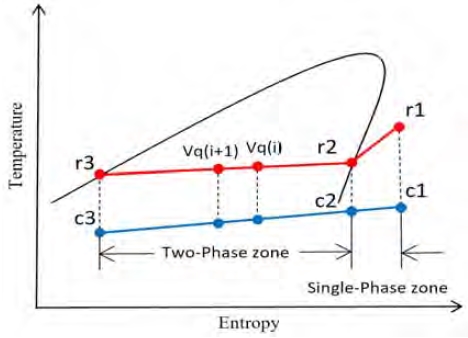
J. S. Kim et al. [4]의 실험에서 사용된 판형 응축기의 분석에 앞서, D. Hu et al. [6]의 연구에서 적용된 해석모델의 검증연구를 수행하였다. Figure 3은 응축기의 T-s선도를 나타낸다.
r1은 작동유체가 응축기로 유입되는 지점이며, 과열증기 상태이다. r2는 작동유체의 포화증기에 해당하는 지점이며, r1에서 r2까지는 작동유체의 단상유동구간이다. r3은 작동유체가 응축기로부터 배출되는 지점이며, 포화액 상태이다. r2에서 r3까지는 작동유체의 상변화가 발생하는 이상유동구간이다. c3과 c1은 각각 응축기내 냉각수 입구 및 출구지점이며, c2는 작동유체가 r2지점일 때 냉각수의 상태를 나타내는 지점이다.
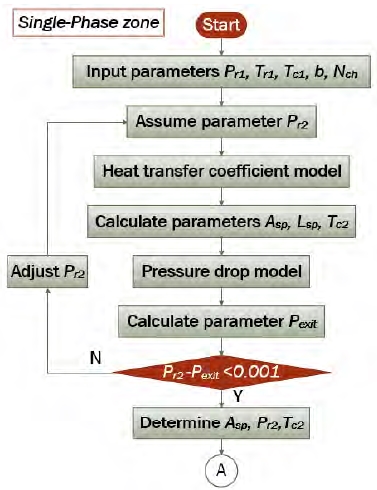
Figure 4는 단상유동구간의 해석 알고리즘 순서도를 나타낸다. 입력하는 프로그램의 초기 값은 r1의 압력(Pr1)과 온도(Tr1), c1의 온도(Tc1), 채널 간극(b) 및 개수(Nch)이다. 여기서, c1지점의 압력은 일정한 값으로 설정하였으며, 냉각수의 압력강하는 무시하였다. r1과 c1지점은 초기 값에 의해 결정되며, r2의 압력(Pr2)은 가정한다. 여기서 정상상태의 에너지보존법칙에 따라 c2지점의 온도(Tc2)가 산정되며, 대수평균온도차(∆Tlm)를 구할 수 있다. 또한 열전달계수모델에서 각각의 열전달계수(hr,hc) 및 총열전달계수(U)가 산출된다. 산출된 대수평균온도차(∆Tlm)와 총열전달계수(U)를 통하여 식 (6)에 따라 단상유동구간의 열전달면적(Asp) 및 판의 길이(Lsp)를 구할 수 있다. 판의 길이(Lsp)는 압력강하모델에 반영되며, 단상유동에서의 마찰계수(f)를 산정한 뒤, 식 (7)에 따라 단상유동구간에서 작동유체의 압력강하(∆P) 및 출구압력(Pexit)을 구할 수 있다. 여기서 가정한 r2의 압력(Pr2)과 산정된 출구압력(Pexit)에서 오차가 0.001이상일 경우, Pr2를 0.001kPa씩 감소시키며 반복계산을 수행한다. 두 값의 오차범위가 만족할 시 반복계산은 종료되고, 단상유동구간에서의 열전달면적(Asp), r2의 압력(Pr2) 및 c2의 온도(Tc2)가 결정된다.
이상유동구간은 건도변화에 따라 작동유체의 상태가 비선형적으로 변화함에 따라 일정한 단위로 구간을 나누어 해석하는 것이 바람직하다. D. Hu et al. [6]의 연구에서는 이상유동구간의 해석방법에 관하여 구체적으로 명시되어 있지 않아, 본 연구에서는 건도를 기준으로 이상유동구간을 나누었다.
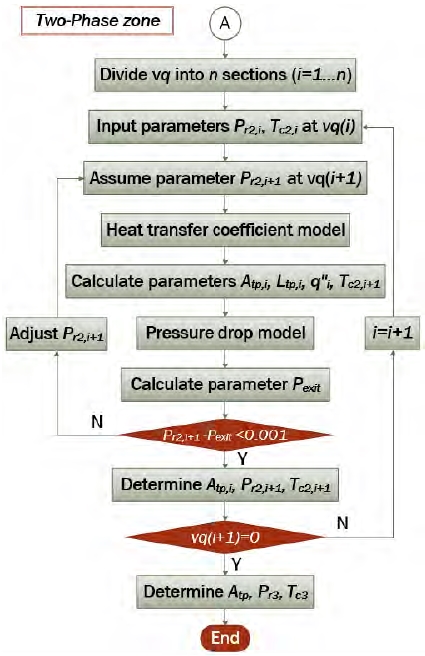
Figure 5는 이상유동구간의 해석 알고리즘 순서도를 나타낸다. 이상유동구간은 건도를 기준으로 n 개의 세부구간으로 나누었다. 첫 번째 세부구간의 입구 측 건도는 포화증기 상태에서 시작되며, 첫 번째 세부구간의 입력 값은 Figure 4의 단상유동구간의 결과인 r2의 압력(Pr2,1) 및 c2의 온도(Tc2,1)의 값이다. 다음으로, 첫 번째 세부구간의 출구 측 건도에 해당하는 압력(Pr2,2)이 가정되며, 이후 열전달계수모델에 의하여 첫 번째 세부구간의 총열전달계수(U)가 산정된다. 또한 에너지보존법칙에 따라 첫 번째 세부구간의 출구 측 건도에 대응하는 냉각수 온도(Tc2,2)가 산정되며, 첫 번째 세부구간의 대수평균온도차(∆Tlm)가 결정된다. 여기서, 이상유동에 해당하는 첫 번째 세부구간의 열전달면적(Atp,1), 판의 길이(Ltp,1) 및 열유속(q″1)이 산정된다. 첫 번째 세부구간의 판의 길이(Ltp,1) 및 열유속(q″1)을 이용하여, 압력강하모델에서 마찰계수(f), 압력강하(∆P) 및 출구압력(Pexit)을 산출한다. 여기서 첫 번째 세부구간의 출구 측 압력(Pr2,2)에 대한 가정 값과 계산된 출구압력(Pexit)의 오차가 0.001이상일 경우, 가정한 압력(Pr2,2)을 0.001kPa씩 감소시켜 반복계산을 수행한다. 두 값의 오차범위 만족시 반복계산은 종료되고, 첫 번째 세부구간의 열전달면적(Atp,1)이 결정된다. 또한 첫 번째 세부구간의 출구 측 건도에 해당하는 작동유체 압력(Pr2,2)과 냉각수 온도(Tc2,2)가 결정된다. 이와 같은 알고리즘으로 결정된 i 번째 유체의 상태량과 가정된 i+1 번째 작동유체의 압력(Pr2,i+1)을 이용하여 특정 세부구간의 열전달면적 및 압력강하를 구한다. 이상유동구간은 n 번째 구간이 되는 i+1 의 건도가 ‘0’이 되는 지점까지 계산을 수행한다. 이상유동구간의 계산이 종료되면, 이상유동구간의 총 열전달면적(Atp), r3의 압력(Pr3) 및 c3의 온도(Tc3)의 값이 결정되면서 순서도가 종료된다. 여기서, 식 (15) ~ 식 (16)을 통하여 판형 응축기의 총 열전달면적(At) 및 총 압력강하(∆Pt) 를 구할 수 있다.
| (15) |
| (16) |
3.2 해석모델 검증결과
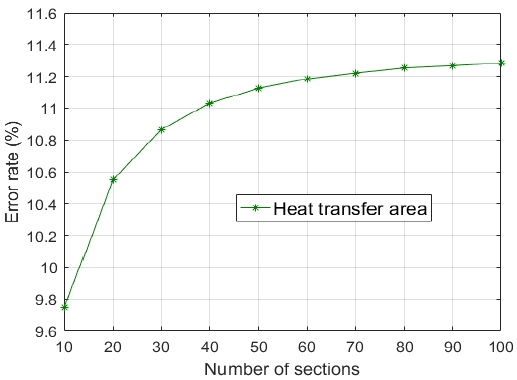
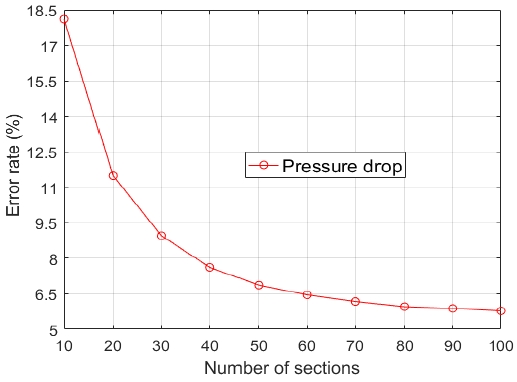
본 연구에서 제시한 알고리즘을 검증하기 위하여 D. Hu et al. [6]의 연구에서 판형 응축기의 운전조건과 연구결과를 참고하였다. 이상유동구간의 세부구간 개수(n)는 열교환기의 해석결과에 지배적으로 영향을 미치는 변수가 될 수 있다. Figure 6과 Figure 7은 각각 이상유동구간의 세부구간 개수(n)에 따른 열전달면적(A) 및 압력강하(∆P)의 수렴성 테스트 결과이다. 두 결과 모두 세부구간 개수(n)가 100개인 경우에 D. Hu et al. [6]의 연구결과 대비 오차율이 수렴되는 결과를 보였다.
Table 1은 수렴된 해석모델의 검증결과를 나타낸다. D. Hu et al. [6]의 연구와 오차율이 발생하는 원인은 다음과 같다. 첫째, 절단오차 때문이다. 예를 들어 D. Hu et al. [6]의 연구에서 명시되어 있는 터빈입구조건이 65.9℃, 475kPa, 터빈출구조건이 47.3℃, 220kPa인 경우 터빈의 효율은 약 85.57%에 달하나, D. Hu et al. [6]의 연구에서 명시한 터빈의 효율은 82.3%에 불과하다. 이러한 차이는 D. Hu et al. [6]의 연구에서 명확하게 명시하지 않은 각 변수의 소수점 이하의 값에서 기인한 것으로 보인다. 둘째, D. Hu et al. [6]의 연구에서 판의 재질을 명확히 알 수가 없어, 본 검증에서는 판의 재질을 티타늄으로 가정하였다. 판의 재질은 총열전달계수(U)의 값을 산출할 시 필요한 판의 열전도도(k)의 값을 결정하므로, 해석에 적지 않은 영향을 미치는 변수이다. 마지막으로 열교환기의 이상유동구간에서 열전달 및 압력강하모델의 적용방법에 관하여 구체적으로 명시되어 있지 않은 점이 오차율 상승에 기인한 것으로 보인다.
그러나 Table 1에서 보인 바와 같이 D. Hu et al. [6]의 연구결과와 본 연구의 결과 중 특히, 압력강하(∆P) 값은 대동소이하므로 본 연구에서 개발한 알고리즘의 신뢰성은 충분한 것으로 사료된다.
4. 실험용 판형 응축기 분석
J. S. Kim et al. [4]의 실험용 판형 응축기의 개선을 위하여, 앞서 검증을 마친 알고리즘을 이용하여 채널 간극(b) 및 채널 개수(Nch)에 따른 실험용 판형 응축기의 열전달면적(A) 및 압력강하(∆P)를 분석하였다. J. S. Kim et al. [4]의 실험에서 사용된 판형 응축기의 기하학적 구조에 대한 사양은 Table 2와 같으며, 분석을 위해 본 연구에서 개발한 알고리즘이 요구하는 초기 값의 조건은 Table 3과 같다.
Figure 8은 채널 간극(b)에 따른 열전달면적(A) 및 압력강하(∆P)의 변화를 나타낸다. 채널 간극(b)이 증가할수록 열전달면적(A)은 증가하나, 압력강하(∆P)는 감소한다. 즉, 채널 간극(b)을 증가시키는 조치는 판형 응축기의 압력강하(∆P)를 줄일 수 있다는 점에서 긍정적이다. 그러나 채널 간극(b)의 증가에 따라 열전달면적(A)이 증가하게 되고 이것은 열교환기의 비용을 증가시키는 결과를 초래한다. 그러므로 적절한 채널 간극(b)을 선정할 필요가 있다. D. Hu et al. [6]은 적절한 채널 간극(b)을 입구압력 대비 압력강하(∆P)가 3%인 조건을 제시하였다. 본 연구의 결과, 채널 간극(b)이 1.6mm인 경우 압력강하가 약 2.95%에 해당한다.
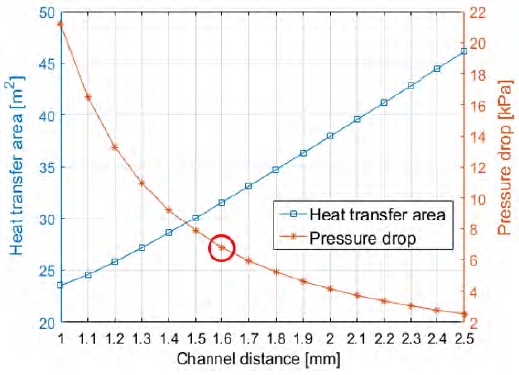
Results of heat transfer area and pressure drop of the plate-type condenser according to the channel distance
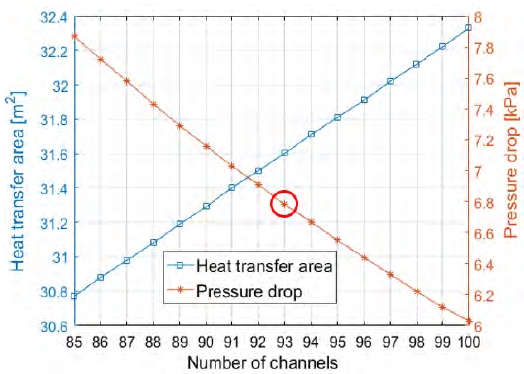
Figure 9는 앞선 결과를 반영하여, 채널 간극(b)이 1.6mm인 상태에서 채널 개수(Nch)에 따른 열전달면적(A) 및 압력강하(∆P)의 변화를 나타낸다. 채널 개수(Nch)가 증가할수록 열전달면적(A)는 증가하며, 압력강하(∆P)는 감소한다. 채널 개수(Nch) 93개에서 압력강하가 3%이내에 달하였으며, 이때 열전달면적(A) 및 압력강하(∆P)는 각각 약 31.60m2, 6.78kPa에 달하였다. 즉, 압력강하가 약 3.31 ~ 10.27%에 달하였던 J. S. Kim et al. [4]의 실험용 판형 응축기는 채널 간극(b) 1.6mm, 채널 개수(Nch) 93개에서 3%이내의 압력강하 개선을 기대할 수 있다.
5. 결 론
본 연구에서는 J. S. Kim et al. [4]의 실험에서 사용된 판형 열교환기 형식인 판형 응축기의 압력강하를 개선하기 위한 연구를 수행하였다. 판형 응축기의 해석을 위하여 D. Hu et al. [6]의 연구를 참조하여, 열전달 및 압력강하모델을 동시에 연산 가능한 알고리즘의 프로그래밍 및 검증을 수행하였다. 그리고 검증을 마친 해석 알고리즘을 이용하여 J. S. Kim et al. [4]의 실험용 판형 응축기를 분석하였으며, 아래와 같은 결론을 얻을 수 있었다.
- (1) 본 연구에서 프로그래밍한 알고리즘이 제시하는 열전달면적 및 압력강하는 D. Hu et al. [6]의 연구에서 명시된 값과 비교하여 각각 약 11.28 %, 5.78 %의 오차율을 보였다. 이러한 오차율의 원인은 수치의 절단오차, 불분명한 판형 열교환기의 판 재질 및 이상유동구간 해석방법 등으로 인하여 발생된 것으로 보인다.
- (2) 채널 간극 및 개수에 따른 J. S. Kim et al.[4]의 실험용 판형 응축기의 열전달면적과 압력강하를 분석한 결과, 채널 간극(b) 1.6mm 이상, 채널 개수(Nch) 93개 이상에서 3%이내의 압력강하를 기대할 수 있다. 추후 실험 시 이번 연구의 결과를 반영하여 판형 응축기의 개선작업이 이루어진다면 보다 향상된 유기랭킨사이클의 효율을 기대할 수 있다.
후속연구로는 본 연구를 바탕으로 작동유체가 압축액유동, 이상유동 및 과열유동의 영역으로 상태가 변하는 판형 열교환기 형식의 증발기에 관하여 추가적인 연구를 진행할 예정이다.
Nomenclature
| A : | heat transfer area [m2] |
| b : | channel distance [mm] |
| Bo : | Boiling number |
| Dh : | hydraulic diameter [m] |
| f : | friction factor |
| G : | mass flux [kg/m2∙s] |
| H : | enthalpy [J/kg] |
| h : | heat transfer coefficient [W/m2∙K] |
| k : | thermal conductivity [W/m∙K] |
| L : | plate length [m] |
| : | mass flow rate [kg/s] |
| Nch : | number of channels |
| Nu : | Nusselt number |
| n : | number of sections |
| P : | pressure [kPa] |
| Pr : | Prandtl number |
| : | heat transfer rate [W] |
| q″ : | heat flux [W/m2] |
| Re : | Reynolds number |
| T : | temperature [K] |
| t : | plate thickness [mm] |
| U : | overall heat transfer coefficient [W/m2∙K] |
| vq : | vapor quality |
| W : | plate width [m] |
| Xm : | mean vapor quality |
| ΔTlm : | log mean temperature difference [K] |
Greeks
| θ : | chevron angle [rad] |
| μ : | viscosity [Pa∙s] |
| θ : | density [kg/m3] |
Subscripts
| c : | cooling water |
| eq : | equivalent |
| g : | gas |
| i : | inlet |
| l : | liquid |
| o : | outlet |
| r : | working fluid |
| sp : | single-phase |
| t : | total |
| tp : | two-phase |
Acknowledgments
Author Contributions
Investigation, J. S. Kim and D. Y. Kim; Methodology, J. S. Kim and D. Y. Kim; Numerical Simulation, J. S. Kim; Writing-Original Draft, J. S. Kim; Writing-Review & Editing, Y. T. Kim and D. Y. Kim; Supervision, D. Y. Kim; Funding Acquisition, D. Y. Kim.
References
- Y. A. Cengel, and A. J. Ghajar, Heat and Mass Transfer, 4th ed., McGraw-Hill, (2014).
- W. S. Janna, Design of Fluid Thermal Systems, 4th ed., CENGAGE Learning, (2015).
-
T. W. Lim, Y. S. Choi, and C. K. Lee, “Design of plate heat exchangers for use in medium temperature organic Rankine cycles”, Heat Mass Transfer, 55(1), p165-174, (2019).
[https://doi.org/10.1007/s00231-018-2446-8]

-
J. S. Kim, D. Y. Kim, and Y. T. Kim, “Experiment on radial inflow turbines and performance prediction using deep neural network for the organic Rankine cycle”, Applied Thermal Engineering, 149, p633-643, (2019).
[https://doi.org/10.1016/j.applthermaleng.2018.12.084]

- Y. A. Cengel, and M. A. Boles, Thermodynamics: An Engineering Approach, 7th ed., McGraw-Hill, (2014).
-
D. Hu, S. Li, Y. Zheng, J. Wang, and Y. Dai, “Preliminary design and off-design performance analysis of an Organic Rankine Cycle for geothermal sources”, Energy Conversion and Management, 96, p175-187, (2015).
[https://doi.org/10.1016/j.enconman.2015.02.078]

- Matlab Manual, Mathworks, (2016).
-
J. R. García-Cascales, F. Vera-García, J. M. Corberán-Salvador, and J. Gonzálvez-Maciá, “Assessment of boiling and condensation heat transfer correlations in the modelling of plate heat exchangers”, International Journal of Refrigeration, 30(6), p1029-1041, (2007).
[https://doi.org/10.1016/j.ijrefrig.2007.01.004]

- G. F. Hewitt, and J. Barbosa, Heat exchanger design handbook, Begell House, (2008).
-
Y. Y. Yan, H. C. Lio, and T. F. Lin, “Condensation heat transfer and pressure drop of refrigerant R-134a in a plate heat exchanger”, International Journal of Heat and Mass Transfer, 42(6), p993-1006, (1999).
[https://doi.org/10.1016/s0017-9310(98)00217-8]

-
W. S. Kuo, Y. M. Lie, Y. Y. Hsieh, and T. F. Lin, “Condensation heat transfer and pressure drop of refrigerant R-410A flow in a vertical plate heat exchanger”, International Journal of Heat and Mass Transfer, 48(25-26), p5205-5220, (2005).
[https://doi.org/10.1016/j.ijheatmasstransfer.2005.07.023]