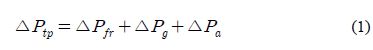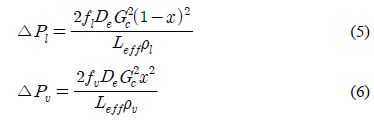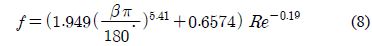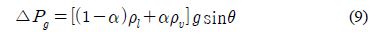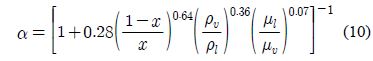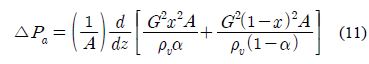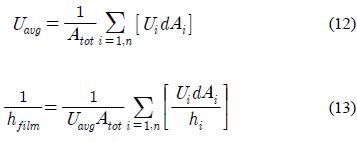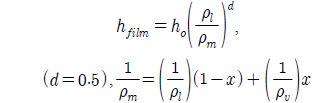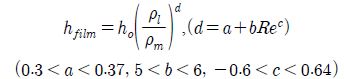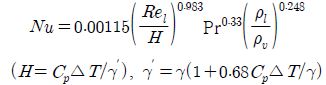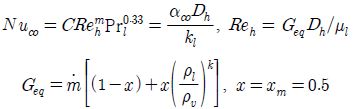Analysis on condensation heat transfer and pressure drop to develop design program for plate heat exchangers

기호설명

d : 밀도 보정계수

f : 마찰인자(Friction Factor)

g : 중력가속도[m/s²]

G_c : 채널 유속 [kg/m²s]

h_film : 응축열전달계수 [W/m²K]

h_o : 단상대류열전달계수 [W/m²K]

i : 엔탈피 [kJ/kg]

k : 전도열전달계수 [W/mK]

L_eff : 유효길이[m]

N_u : 넛셀 수

ΔP : 압력강하 [Pa]

Pr : 프란틀 수

q^″ : 열 유속 [W/m²]

Re : 레이놀즈 수

ΔT_lm : 대수평균온도차 [K]

U : 총괄열전달계수 [W/m²K]

u_p : 포트유속[m/s]

X_tt : Lockhart-Martinelli Parameter

그리스 문자

α : 기공률(Void Fraction)

β : 쉐브론각[degree]

ρ : 밀도[kg/m³]

μ : 점도[Pa ∙ s]

ϕ : Two-Phase Multiplier

하첨자

aυg : 평균

c : 저온측

ch : 채널

h : 고온측

in : 입구

l : 액체

out : 출구

tp : 이상

υ : 기체

w : 벽

1. 서 론

판형열교환기(PHEs: Plate Heat Exchangers)는 에너지 효율 향상에 큰 역할을 하고 있으며 주로 단상에서 적용이 되었지만 더 높은 에너지 효율을 위해 잠열까지 회수할 수 있는 이상유동에 관한 연구가 이루어지고 있다. Annaiev et al. [1]은 실험을 통하여 수평관을 적용한 단상과 이상의 응축열전달 상관식을 도출하였고, Wang & Zhao. [2]는 판형을 이용하여 새로운 무차원을 접목시켜 상관식을 도출했다. Wang et al. [3]은 Annaiev et al. [1] 의 상관식을 판형에 적용하고 상관식을 레이놀즈 수에 대한 함수로 보정하였다. Würfel & Ostrowski [4]은 이상유동의 열전달 상관식을 종합하고 실험을 통해 특정 레이놀즈 수의 범위에 맞는 상관식을 도출하였다. Lockhart & Martinelli [5]는 기체와 액체의 압력강하 비인 Lockhart & Martinelli Parameter와 Two-Phase Multiplier의 상관식을 유도했다. 본 연구는 판형열교환기의 설계프로그램 개발을 위해 실제 설계되는 레이놀즈 수 범위에 대하여 위의 상관식을 사용하여 설계인자를 계산하였으며, 그 결과를 상용코드와 비교하였다.

2. 계산검증을 위한 식의 선정

2.2 열전달 상관식

이상유동의 열전달은 유동양식에 따른 각기 다른 열전달계수가 적용되어야 한다. 하지만 프로그램개발에 있어 간단한 수식을 필요로 하며 상관식은 대부분 실험에 의존한다. Table 1은 선행연구에 의해 제시된 열전달 상관식이다. 실제 판형열교환기의 설계범위(Re > 2000)에 적용될 수 있는 Table 1의 상관식들 중 Annaiev et al. [1] 의 상관식이 적용가능하다고 판단되었다.

Table 1

Correlation for condensation heat transfer coefficient

3. 계산절차 및 해석 조건

3.1 계산절차

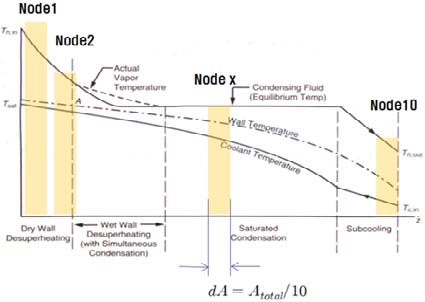
Wang et al. [3]은 응축과정의 건도변화가 비선형이며 압력과 열전달이 서로 영향을 미치기 때문에 100개의 절점으로 나눠 단계적으로 계산을 수행하였다. 본 연구에서는 Figure 1과 같이 전체 면적에 대하여 과열영역, 응축영역, 과냉영역을 총 10개의 절점으로 나누었다.

Figure 1

Node & Temperature profile

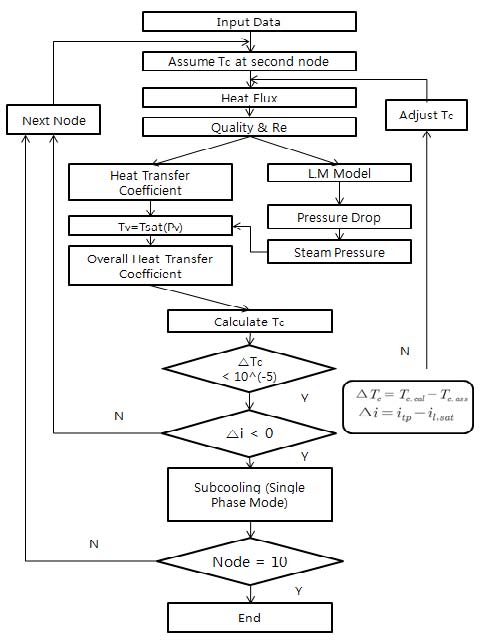
이상유동에 관한 계산순서는 Figure 2에 나타냈다.

계산과정의 첫 번째 단계는 저온 측의 온도를 추정하는 것이다. 추정된 온도로 인해 열이 가정되면 등 간격으로 나눠진 면적으로 인해 열 유속이 결정된다. 고온 측의 증기 엔탈피로 건도를 계산할 수 있으며 기체 및 액체의 레이놀즈 수를 알 수 있다. 레이놀즈 수로 인해 열전달계수 및 압력강하를 추정할 수 있다. 단상에 관한 상관식은 Ko et al. [9]의 상관식을 사용했다. 압력강하는 Lockhart & Martinelli 모델을 이용해 Multiplier가 계산된다. 고온 측의 압력강하는 대류열전달계수 및 총괄열전달계수에 영향을 미쳐 증기의 포화 온도를 결정한다. 응축 열전달계수는 다양한 수식이 있었지만 Re > 2000의 레이놀즈 수 범위에 적용 가능하다고 판단이 된 Annaiev et al. [1]의 상관식을 이용했다. 가정된 열 유속과 총괄열전달계수로 저온 측의 온도가 계산된다. 계산된 저온 측 온도와 가정된 저온측 온도의 차이가 특정조건을 만족하면 다음 절점을 계산한다. 그렇지 않다면 조건을 만족할 때 까지 반복계산이 수행된다.

Figure 2

Two-Phase Flow Chart

3.2 해석범위 및 조건

Table 2는 특정 판의 모델 A, B, C, D에 대하여 PHEs의 실제 설계되는 포트 유속을 기준으로 운전 가능한 압력범위를 선정하고 과냉영역까지 진행 될 수 있는 출구 온도를 선정했다.

Table 2

Range of test in two-phase flow

Table 3은 Table 2의 해석영역 중 포트입구유속이 40m/s이며 레이놀즈 수가 약 10⁴에 관한 해석조건이다.

Table 3

Test condition of A on Rel ≈ 104

4. 상관식의 검증

4.1 건도의 변화

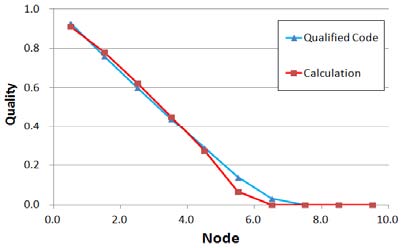
Figure 3은 상용코드와 상관식을 사용하여 계산한 건도 변화이다. 절점 5 - 6 사이에서 응축되는 것을 확인할 수 있으며 상관식은 절점 5 - 6 사이를 제외하고는 비교적 차이가 없다.

Figure 3

Variation of quality

4.2 국소 응축 열전달계수

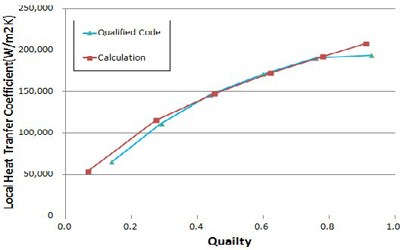
Figure 4는 상용코드와 상관식의 건도에 따른 국소 응축열전달계수의 변화를 나타낸다. 건도 1에서 건도 0으로 접근할 때 채널내의 막이 두꺼워져 국소 응축 열전달 계수는 감소한다.

Figure 4

Local Heat Transfer Coefficient

4.3 국소 압력강하

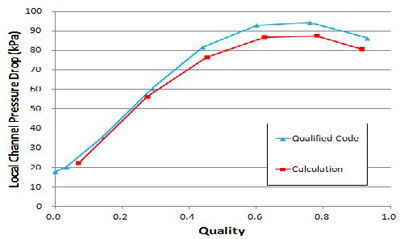
Figure 5는 상용코드와 상관식을 이용한 건도에 따른 압력강하 변화를 나타낸다. 응축이 되면서 기체의 속도가 느려지므로 압력강하는 감소한다.

Figure 5

Local pressure drop

4.4 온도의 변화

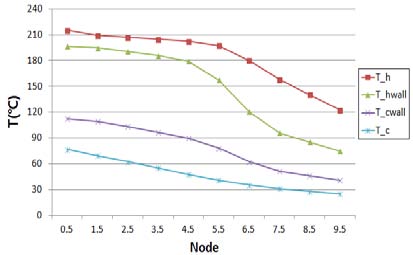
Figure 6은 상관식을 사용하여 평균 절점에 따른 온도변화를 나타낸다. 계열의 T_h는 고온 측의 온도이며 wall은 벽 온도이며 T_c는 저온 측 온도이다. 전반적으로 Table 3의 입 출구 온도범위에 해당하는 변화를 보이고 있으며 절점 5 – 6사이에서 건도가 0 이 되므로 고온 측과 저온 측의 온도차가 제일 크다.

Figure 6

Temperature profile

4.5 평균 열전달계수 및 채널압력강하

평균열전달의 수식은 식 (12), 식 (13)과 같다[7].

Table 4는 식 (12) 및 (13)을 이용한 평균 열전달계수와 식 (1)을 이용한 절점 10까지의 채널 압력 강하를 나타낸다. 오차율 2%이내를 나타낸다.

Table 4

Average coefficients

4.6 Flow Regime 의 평가

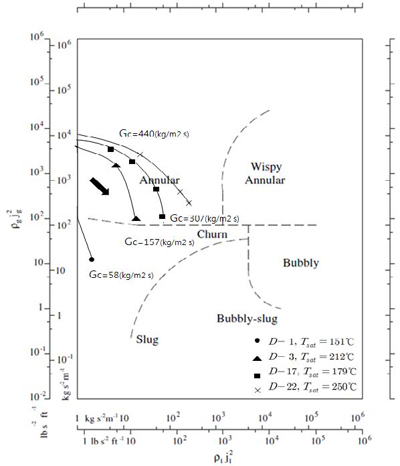
설계영역에 대한 유동양식 맵은 아직 연구된바 없다. 하지만 대략적인 유동양식을 평가하기 위해 Table 2의 특정 결과를 Hewitt & Roberts [10]의 유동양식 맵에 나타내면 Figure 7과 같다. 각 모델의 질량유속을 증가시키면 쉽게 Annular Flow 형태를 나타냈다. 화살표 방향은 응축되면서 Churn Flow의 형태를 나타내려는 특성을 가진다.

Figure 7

Estimation of flow regime by Hewitt & Roberts [10]

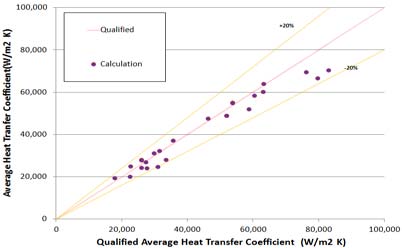
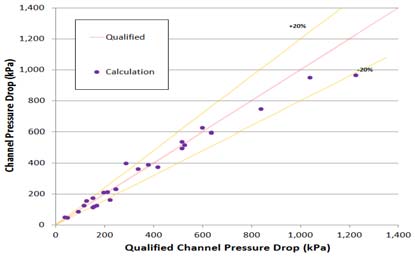
4.7 상관식의 오차

4.1~4.5는 Table 3의 해석영역 중 특정조건에서 해석한 결과를 나타낸다. 상관식은 해석영역에 대한 전반적인 평가가 이루어져야 한다. Figure 8과 Figure 9는 상용코드를 기준으로 한 상관식의 오차분포를 나타낸다. 점의 분포가 적색 선에 가까울수록 상용코드의 결과와 동등함을 의미한다. 오차는 비교적 20%이내의 범위 내에 분포 되어있다. 오차의 원인은 상용코드와 알고리즘에 적용된 h₀및 d에 의한 것으로 판단된다.

Figure 8

Distribution of average heat transfer coefficient

Figure 9

Distribution of channel pressure drop

5. 결 론

본 연구는 국내 판형열교환기의 설계프로그램 개발을 목적으로 기초자료를 토대로 판형 열교환기에 적용될 수 있는 이상유동 상관식을 확보하는 것이며 결과는 다음과 같이 요약된다.

1. 기존의 제시된 상관식을 종합하여 판형열교환기의 작동범위에 알맞은 열전달 및 압력강하의 상관식을 확보하였다.

2. 열전달과 압력강하를 동시에 계산하기 위한 계산 알고리즘을 제시하였다.

3. 해석 범위에 대하여 상용코드와 비교 시 20% 이하의 오차가 나타나므로 설계프로그램의 국산화가 가능하다고 판단된다.

References

• E. P. Annaiev, L. D. Boyko, and G. N. Kruzhilin, “Heat transfer in the presence of steam condensation in a horizontal tube”, Proceedings 1st International Heat Transfer Conference, Part Ⅱ, p290, (1961).
• Z. Wang, and Z. Zhao, “Analysis of performance of steam condensation heat transfer and pressure drop in plate condensers”, Heat Transfer Engineering, 14(4), p32-41, (1993). [https://doi.org/10.1080/01457639308939809]
• L. Wang, R. Christensen, and B. Suden, “An experimental investigation of steam condensation in plate heat exchangers”, International Journal of Heat Exchangers, 1, p125-150, (2000).
• R. Würfel, and N. Ostrowski, “Experimental investigations of heat transfer and pressure drop during the condensation process within palte heat exchangers of the herringbone-type”, International Journal of Thermal Sciences, 43(1), p59-68, (2004).
• R. W. Lockhart, and R. C. Martinelli, “Proposed correlation of data for isothermal two-phase, two-component flow in pipes”, Chemical Engineering Progress, 45(1), p39-48, (1949).
• V. P. Carey, Liquid vapor phase change phenomena, Hebron, KY, USA, Taylor & Francis, (1992).
• Heat Transfer Research Incorporation, Design Manual, College Station Texas 77845 USA, (2003).
• G. L. Shires, G. L. Shires, and T. R. Bott, Proces Heat Transfer, CRC Press, Inc, (1994).
• J. H. Ko, Y. H. Song, and K. H. Park, “Study on Design Factor and Design-code Development for Plate Type Heat Exchangers”, Journal of the Korean Society of Marine Engineering, 36(8), p1003-1009, (2012). [https://doi.org/10.5916/jkosme.2012.36.8.1003]
• G. F. Hewitt, and D. N. Roberts, Studies of Two-Phase Flow Patterns by Simultaneous X-ray and Flash Photography, AERE-M 2159, Her Majesty’s Stationery Office, London, (1969).