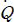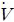Numerical analysis for heat transfer and pressure drop characteristics of “Shell-tube” heat exchanger with various baffle factor
In numbers of kinds of heat exchanger, the shell-tube heat exchanger is the most commonly used type of heat exchanger in the industry field. In order to improve the thermal performance of the heat exchanger, this study was analyzed heat transfer characteristics according to arrangement of baffle and direction of baffle and bump phase of baffle about shell-tube heat exchanger using appropriate SST (Shear Stress Transport) turbulence model for flow separation and boundary layer analysis. As the boundary condition for CFD (Computational Fluid Dynamics) analysis, the inlet temperature of shell side was constantly 344 K and the variation of the water flow rate was 6, 12, 18 and 24 l/min. As the result of analysis, zigzag baffle arrangement enhances heat transfer rate and pressure drop. Furthermore, in the direction of the baffle, heat transfer rate is more improved with vertical type and angle 45° type than existing type, and pressure drop was little difference. Also, the bump shape of baffle surface contributes to heat transfer rate and pressure drop improvement due to the increased heat transfer area. Through analysis results, we knew that the increase of the heat transfer was influenced by flow separation, fluid residual time, contact area with the tube, flow rate, swirl and so on.
초록
셀-튜브 열교환기는 산업분야에서 가장 널리 사용되는 열교환기이다. 열교환기의 열적 성능을 개선하기 위하여 셀-튜브 열교환기에 대해 배플의 배치, 배플의 방향, 배플의 표면의 돌기형상 등의 인자를 변경하였으며, 유동의 박리 및 경계층해석에 적절히 이용되는 SST 난류모델을 적용하여 열전달특성을 고찰하였다. CFD해석시 경계조건는 셀측의 입구온도를 344K로 일정하게 하고, 물의 유량을 6, 12, 18, 24 l/min로 변화시켰다. 그 결과로는 지그재그형 배치가 열전달률 및 압력강하가 향상되는 것으로 나타났으며, 배플의 방향은 기존형보다 수직형 및 각도 45°형이 열전달이 향상되는 것으로 나타났고, 압력강하는 거의 차이가 없었다. 또한 배플의 돌기형상은 열전달면적을 증가시킴으로써 열전달률 및 압력강하가 향상됨을 알 수 있었다. 해석결과를 통하여 열전달 증가가 유동의 박리, 유체의 체류시간, 튜브와의 접촉면적, 유량, 와류 등에 따라 크게 영향을 받는다는 것을 알 수 있었다.
Keywords:
Shell-Tube Heat Exchanger, CFD, Baffle, Heat Transfer, Pressure Drop, 셀-튜브 열교환기, 전산유체역학, 배플, 열전달, 압력강하기호설명
Cp : 정압비열[kJ/kg·K]
D : 관지름 [mm]
g : 중력가속도 [m/s2]
κ : 열전도계수 [W/m·K]
L : 길이 [mm]
P : 압력 [N/㎡]
T : 온도 [K]
t : 두께 [mm]
υ : 속도 [m/s]
ρ : 밀도 [kg/m3]
µ : 총점성계수 [N·s/m2]
µι : 층류점성계수 [N·s/m2]
µt : 난류점성계수 [N·s/m2]
k : 난류운동에너지 [m2/s3]
ω : 소산율 [m2/s3]
β : 체적팽창계수 [1/K]
1. 서 론
열교환기는 상이한 온도에 있는 다른 두 유체 사이의 열전달을 효율적으로 이동시키는 장치로서 화학공정, 가열과 공기정화, 기름정유, 폐열회수, 제조공업 등에 가장 널리 이용되고 있어 그 용도에 맞게 다양한 형태의 구조로 제작되고 있다. 특히 에너지에 대한 이용, 개발 및 절약의 중요성이 높아지면서 열교환기의 요구 성능도 상당히 높아지고 있다. 이들의 열교환기 중에 셀-튜브 열교환기는 장점으로 동심 원관 열교환기보다 체적에 대한 열전달 표면적의 비를 증가시켜 전열특성을 향상시킬 수 있으며, 또한 다양한 크기와 유동형태로 쉽게 제작할 수 있어 구조재료의 선택범위가 넓어서 조작의 탄력성이 크다. 보통 열교환기의 개발추세는 열교환기의 크기와 비용을 줄이면서도 기존의 열교환기와 동일한 열전달성능을 나타내기 위한 연구들이 대부분이다[1].
셀-튜브 열교환기에 대한 연구동향으로서 Li와 Kottke[2]는 열교환기의 설계인자인 배플을 관군에 설치하여 원통 내에 유체의 흐름이 관군과 직교가 되게 하고 유속을 높여 열교환기의 셀 내에서 혼합난류강도를 증가시켜 열전달 성능을 향상시켜 나타냈으며, Lee et al. [3]은 원통다관형 열교환기인 Bell-Delaware법을 사용하여, 다양한 값의 배플 간격과 배플수에 대하여 유동조건을 변화시켜가며 열전달특성을 고찰하였다. Oh et al. [4]은 실험과 수치해석을 통해 단일관 열교환기에 대해 주어진 유량조건에서 배플의 높이 및 수에 최적값을 도출하기 위한 변수연구를 수행하였다. Hong et al. [5]은 셀측의 유로길이와 방향전환을 최소화하면서도 유체혼합 및 대류열전달을 효과적으로 증진시킬 수 있는 오리피스 배플과 원형핀의 조합으로 구성되는 환형 배플을 제시하기 위한 연구를 수행하였다. Shin et al. [6]은 단일직관 쉘-튜브 열교환기에 대해 수치해석을 통해 열교환기 유체의 열전달량에 유효하게 영향을 미치는 인자들을 확인하는 연구를 수행하였다. Lee et al. [7]은 원통다관형 열교환기의 설계모델에 대한 내부유동 형상 및 열전달특성을 파악하기 위해서 열전달을 향상시키는 설계인자로 Sealing Strip의 위치 및 크기와 작동조건에 따른 열전달특성을 고찰하였다. Lim et al. [8]은 원통 다관형 열교환기의 관의 크기와 배플수는 동일하게하고 오일측의 입구온도와 오일유량을 변화시켜 원통 내의 3종류의 관수(9, 13, 19)들에 대하여 원통셀측 총합열전달을 비교 및 분석하였다. 또한, Bae et al. [9]은 열교환기에 대하여 실험적으로 배플의 크기, 유체의 온도 및 속도에 따른 열전달 및 압력강하 특성을 연구하였다.
본 연구에서는 먼저 Oh et al. [4]이 수행한 연구결과와 비교하기 위해 수치해석 모델에 대한 검증을 수행한 후, 이를 토대로 열교환기 내의 배플의 배치 및 모양, 배플의 돌기형상 등의 다양한 인자를 적용하여 열전달 및 압력강하 특성을 고찰하였다.
2. 이론해석
2.1 해석 모델
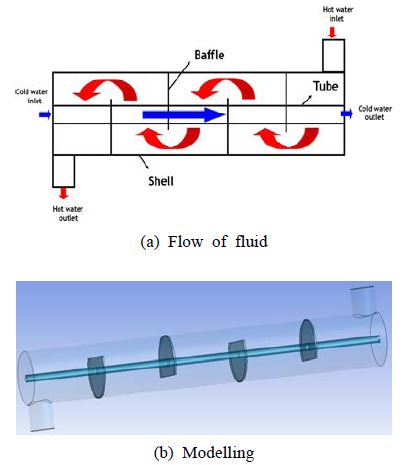
본 연구에서는 ANSYS v.14의 전처리 프로그램(Pre-Processor)인 Design Modeler를 이용하여 셀-튜브 열교환기를 모델링하였으며, 해석모델의 형상 및 제원은 각각 Figure 1 및 Table 1에 나타내었다. 여기서 셀표면 및 튜브면은 단열상태로 가정하였다.
2.2 지배방정식
열교환기의 내부는 3차원 정상상태, 비압축성 난류유동으로 가정하였으며, 지배방정식은 기본적인 연속방정식, 운동량방정식 및 에너지방정식을 사용하였고, 난류모델로는 기존의 난류모델에 비해 유동의 박리나 경계층 영역의 해석에서 우수한 성능을 보인다고 알려진 SST(Shear Stress Transport) k-ω 난류모델을 사용하였다[10]. 이 SST k-ω모델은 난류점성계수의 계산을 위해 난류운동에너지 k와 비소산율ω의 식을 풀이하여 구한다. 속도-압력 연성에 대해서는 Patankar에 의하여 제시된 SIMPLE 알고리즘을 사용하였다[11][12].
2.3 수치해석
Figure 2는 전산해석에서 사용된 약 60만개로 구성된 격자계를 나타내고 있다. 물리적 구배가 심하게 나타날 것으로 예상되는 유체부와 고체부가 만나는 부분에는 좀 더 조밀하게 격자를 생성하도록 하였다. 본 연구의 해석코드는 Fluent v.14을 사용했고, 수치해석을 위한 경계조건은 Table 2에서 나타내고 있으며, 입구 속도 및 온도의 범위는 난류 민감도평가를 수행하기 위해서 Oh et al. [4]이 연구한 실험값을 적용하였다.
2.4 수치해석의 타당성 검증
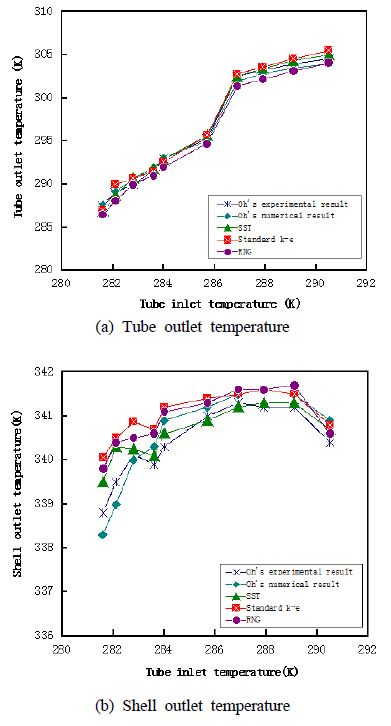
본 절에서는 수치해석 결과의 타당성을 검증하기 위한 분석이 수행되었다. Oh et al. [4]이 수행한 실험 및 해석의 결과와 비교하기 위해 동일한 기하학적 형상 및 입구속도조건에 대하여 얻어진 출구온도값을 비교하였다. 최적의 난류모델 선정을 위해 Standard k - ε, RNG(Re-Normalization Group) k - ε, SST 난류모델[10]를 적용하여 수행하였으며, 그 해석결과를 Figure 3에 나타내었다. 이 3가지 난류모델에 대한 민감도 분석을 수행한 결과로는 SST 난류모델이 가장 실험값과 근사한 결과를 나타내었다. 따라서 본 연구에서는 근사한 결과를 보인 SST 난류모델을 기본 난류모델로 선정되었다.
3. 결과 및 고찰
3.1 배플 배치에 따른 열전달 및 압력특성
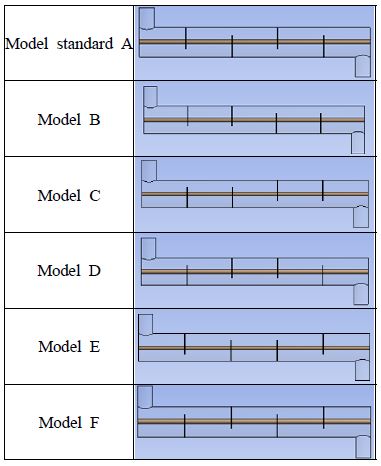
Table 3은 배플 배치에 따른 열전달 및 압력강하의 특성을 고찰하기 위한 모델의 종류를 나타내고 있으며, 온도, 유량, 압력 등의 경계조건은 Table 2의 값을 적용하였다.
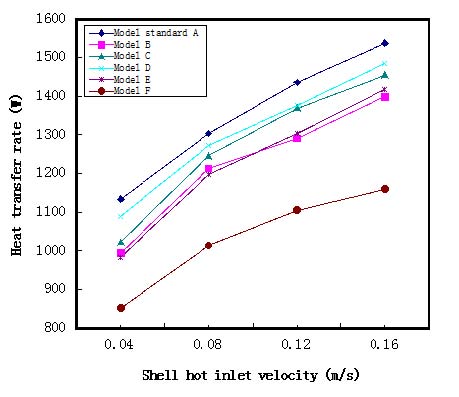
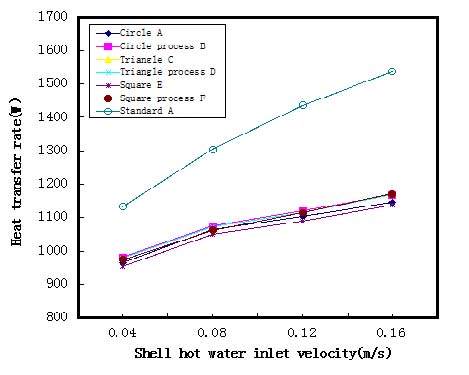
Figure 4는 유속 및 배플 배치에 따른 열전달의 특성을 나타낸 것이다. 그 결과로 유속의 증가에 따라 열전달이 증가됨을 알 수 있으며, 배플 배치의 특성은 기존 배치인 A모델이 가장 높게 나타났다. 또한 B모델과 E모델보다는 C모델과 D모델이 열전달이 더 높게 나타나고 F모델이 가장 낮게 나타났다. 이는 배플 배치 때문에 유체가 유입 할 때부터 유체가 배플을 지난 소요하는 시간이 달라서 유체가 튜브와의 접촉시간이 다름으로써 열전달 특성이 각각 다르게 변화하는 것을 알 수 있었다.
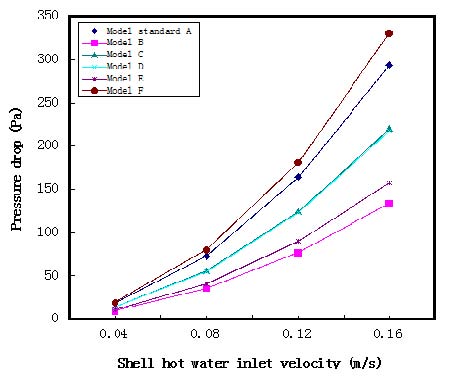
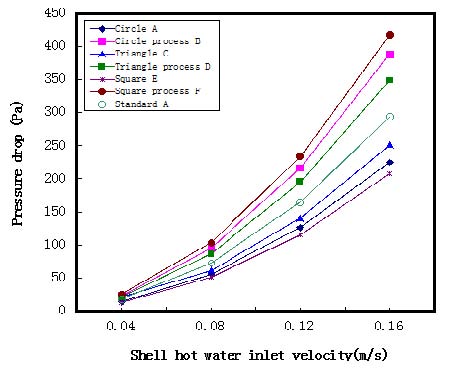
Figure 5은 유속 및 배플 배치에 따른 압력강하의 특성을 나타낸 것이다. 그 결과로 유속의 증가에 따라 압력강하가 크게 나타남을 알 수 있으며, 기존의 배플 배치인 F모델이 가장 크게 나타났고, B모델과 E모델보다는 A, C, D모델이 압력강하가 더 크게 나타났다. C모델과 D모델이 압력강하가 비슷한 나타났다. 이는 기존의 배플 배치 A모델이 지그재그 형상으로 와류현상이 규칙적으로 나타남으로써 열전달 및 압력강하를 증가시킨 것으로 판단된다.
3.2 배플 방향에 따른 열전달 및 압력특성
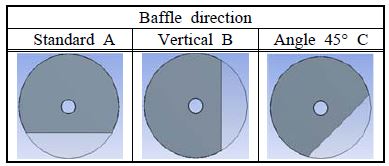
Table 4는 배플 방향에 따른 열전달 및 압력강하의 특성을 고찰하기 위해 모델의 종류를 나타내고 있으며, 온도, 유량, 압력 등의 경계조건은 배플 배치와 동일한 해석을 도출하기 위하여 Table 2의 값을 적용하였다.
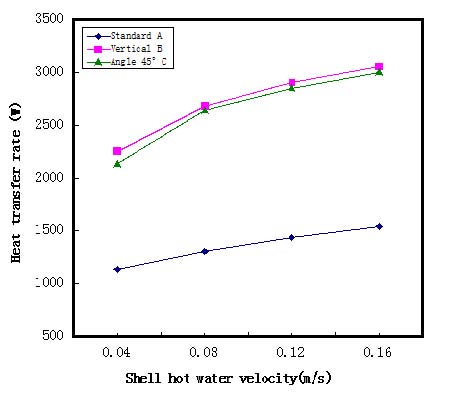
Figure 6은 유속 및 배플 방향에 따른 열전달의 특성을 나타낸 것이다. 그 결과로 유속의 증가에 따라 열전달이 증가됨을 알 수 있으며, 특히 수직형 B모델이 각도 45°형 C모델보다 열전달특성이 더 높게 나타남을 알 수 있다. 이는 유체가 유입 할 때부터 유체가 y방향 수직으로 유입된 유동의 회전(Swirl)이 y방향만이 아닌 y-x방향으로 모두 나타남으로 유로의 시간이 상대적으로 길어져서 수직형 B모델이 각도 45°형 C모델보다 열전달이 더 충분히 일어나 열전달이 더 향상됨을 알 수 있다.
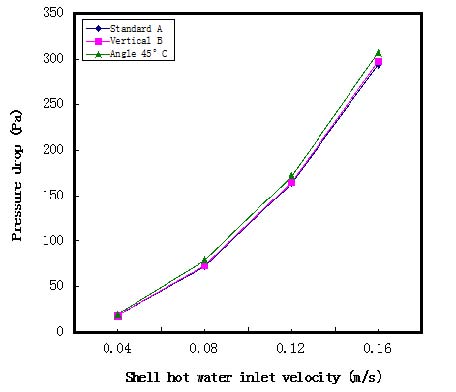
Figure 7은 유속에 따른 배플 방향에 관한 압력강하의 특성을 나타낸 것이다. 그 결과로 유속의 증가에 따라 압력강하가 크게 나타남을 알 수 있으며 모델 A>B>C 순으로 압력강하가 크게 나타남을 보이며, 모델 A, B, C의 배치와 면적이 다 같고 방향만 다르므로 모델 A, B, C의 압력강하의 특성은 미미한 차이로 거의 비슷한 수준으로 나타났다.
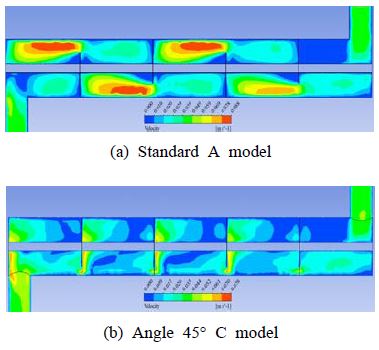
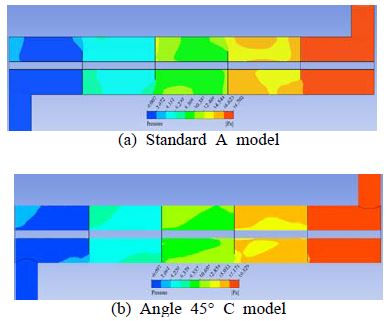
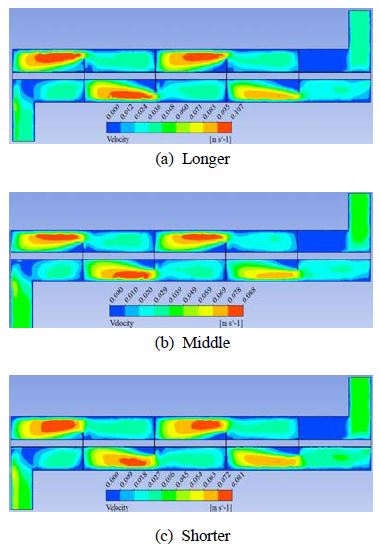
Figure 8과 Figure 9는 셀의 입구유량이 6 l/min 조건에서 기본형 A모델과 각도 45°형 C모델의 배플 방향에 대하여 일반적인 환형 배플이 장착된 단일관 열교환기의 내부의 중간부분의 유동장 및 압력장의 특성을 나타낸 것이다.
유체가 배플을 지날 때 유체속도가 기본형 A모델는 각도 45°형 C모델보다 더 느려져서 유체가 튜브와의 접촉시간이 길어짐으로써 열전달특성이 더 증가하는 것으로 사료된다.
따라서 이는 튜브근처에서 속도의 크기 때문에 튜브와의 접촉시간이 열전달특성에 영향을 미친다는 것을 알 수 있다. 결과적으로 기본형 A모델보다 각도 45°형 C모델이 열전달 특성은 큰 폭으로 향상되는 반면에 압력강하 특성은 약간 크게 나타남을 알 수 있었다.
3.3 배플 돌기형상에 따른 열전달 및 압력특성
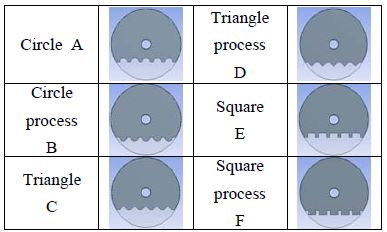
Table 5는 배플 돌기형상에 따른 열전달 및 압력강하의 특성을 고찰하기 위해 모델의 종류를 나타내고 있으며, 온도, 유량, 압력 등의 경계조건은 배플 배치와 동일한 해석을 도출하기 위하여 Table 2의 값을 적용하였다.
Figure 10과 Figure 11는 유속에 따른 배플 돌기형상에 관한 열전달 및 압력강하의 특성을 나타낸 것이다. 그 결과로 유속의 증가에 따라 열전달이 증가됨을 알 수 있으나 Table 5에서 나타난 배플의 돌기형상에 따라 다소 차이는 있지만 기준 배플 형태가 열전달특성이 가장 높은 것으로 나타났다. 그리고 압력강하가 가장 큰 것은 Square process F형으로 나타났다. 이는 Square process F형는 배플의 면적이 제일 커서 유체가 배플을 통과한 면적이 제일 작아지기 때문이다. 따라서 Figure 11에서는 셀 내부의 유체를 동일한 조건에서 전열면적은 배플의 높이에 따라 커짐으로 셀 입.출구의 압력강하도 크게 발생함으로 돌기형태에 따른 배플의 전열면적이 큰 F>B>D>Standard A>C>A>E 모델 순으로 압력강하가 낮아짐을 알 수 있었다.
이는 Figure 12에 나타난 돌기크기와 같이 돌기면적을 크게 하거나 또는 작게 하는 유동형태에 따른 유동장의 해석결과를 Figure 13에서 나타난바와 같이 배플 주위에서 유체의 박리현상, 속도의 크기, 와류생성 등의 영향을 받는 유동형태에 따라 열전달 및 압력강하의 특성이 달라짐을 보여 알 수 있다.
4. 결 론
본 연구에서는 배플을 가지는 셀-튜브 열교환기의 셀측 및 튜브측의 입구속도조건을 변경하여 Oh et al. [4]의 실험 및 해석 값과 비교하여 검증하였으며, 배플의 배치, 배플의 방향, 배플의 돌기형상 등을 적용하여 열전달 및 압력강하에 미치는 영향을 고찰한 결과는 다음과 같다.
(1) 배플이 있는 셀-튜브 열교환기의 열전달특성을 정확히 해석하기 위해서는 난류모델 중에 SST 난류모델을 적용하는 해석방법이 가장 적합하게 나타났다.
(2) 배플 배치에 따른 열전달 및 압력강하의 특성은 일정한 조건에서 유체가 배플을 통과하여 유체의 체류시간을 고려해 볼 때 기본 모델이 지그재그형상으로 와류현상이 규칙적으로 나타남으로써 가장 유리함을 알 수 있었다.
(3) 배플의 설치방향에 따른 열전달 및 압력강하 특성은 6 l/min의 동일 유량조건에 대해서 유체가 튜브와의 접촉시간이 길수록 열전달이 증가됨을 알 수 있으며, 수직형 B모델이 열전달 및 압력강하의 특성에서 가장 양호하게 나타났다.
(4) 배플의 돌기형상에 따라 전열면적을 증가하는 형태가 열전달이 향상되는 뿐만 아니라 배플의 크기로 인한 유체의 박리현상, 유량, 와류 등이 열전달에 크게 영향을 미치는 것을 알 수 있었다.
References
- M. Kovarik, “Optimal heat transfer”, Journal of Heat Transfer Ⅲ, American Society of Mechanical Engineers, p287-293, (1989).
-
H. Li, and V. Kottke, “Effect of baffle spacing on pressure drop and local heat transfer in shell-and-tube heat exchangers for staggered tube arrangement”, International Journal of Heat and Mass Transfer, 41(10), p1303-1311, (1998).
[https://doi.org/10.1016/S0017-9310(97)00201-9]

- S. C. Lee, Y. W. Jo, and S. C. Nam, “Effect of baffle parameters on heat transfer in shell and tube heat exchangers”, Transactions of the Korean Society of Mechanical Engineers B, 21(1), p185-194, (1997), (in Korean).
- G. N. Oh, Y. D. Jun, and K. B. Lee, “Research of heat transfer characteristics with baffle parameters in shell and tube heat exchanger”, Korean Society of Mechanical Engineers, 22(9), p599-604, (2010), (in Korean).
- J. A. Hong, J. D. Jun, and K. B. Lee, “A simulation do single-tube heat exchanger with annular baffles”, Proceeding of the Society of Air-conditioning and Refrigerating Engineers of Korea, p1029-1034, (2012), (in Korean).
- Y. H. Shin, H. D. Jeong, J. H. Lee, and H. S. Chung, “A numerical study of heat transfer and flow characteristics in shell and tube heat exchanger”, Proceeding of the Society of Air-conditioning and Refrigerating Engineers of Korea, p1070-1073, (2011), (in Korean).
- S. H. Lee, M. S. Lee, and N. K. Hur, “Numerical analysis on heat transfer and flow in the shell and tube heat exchanger”, Journal of Computational Fluids Engineering, 12(3), p9-13, (2007), (in Korean).
-
T. W. Lim, and D. H. Cho, “Study on heat transfer characteristic of shell and tube heat exchanger with plate fin”, The Korea Academia-Industrial cooperation Society, 10(1), p46-51, (2009), (in Korean).
[https://doi.org/10.5762/KAIS.2009.10.1.046]

- O. D. Bae, S. H. Jun, and S. H. Yun, “A study on heat transfer characteristics and pressure drop of heat transfer by baffle cut rate”, Proceedings of the Korea Society of Marine Engineers, p172-177, (2005), (in Korean).
- ANSYS Fluent Theory Guid, ANSYS Fluent, 14, (2013).
- J. Y. Park, and J. H. Baek, “A comparative study of PISO, SIMPLE, SIPMLE-C algorithms in 3-dimensional generalized coordinate systems”, Transactions of Korean Society for Computational Fluids Engineering, 1, p26-34, (1996), (in Korean).
- H. G. Myung, CFD introduction, 1st Edition, Munundang, p323-328, (2002), (in Korean).