스크러버 세정수 배출 규제에 따른 노즐 직경 설계에 관한 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 IMO 규정에 따라서 선박의 스크러버 세정수의 pH 회복을 위한 노즐 직경 설계에 관한 수치해석적 연구를 수행하였다. 선박의 스크러버 세정수는 배출지점으로부터 4m에서 pH 6.5 이상이 되어야 한다고 규정되어있다. 이론적인 산-염기 화학반응을 이용하여 적정 곡선을 구하고 pH 6.5 일 때의 희석비 및 체적 분율을 계산하였다. 그리고 CFD 확산 해석을 수행하여 배출 속도와 노즐 직경 변화에 따른 체적 분율을 계산하였다. 해석결과에 의하면 배출 속도는 확산에 큰 영향을 미치지 않는 것으로 나타났으며, 노즐의 직경이 확산에 영향을 미치는 주요 변수로 나타났다. 수치해석 결과를 토대로 희석비에 따라서 배출지점으로 4m 에서 pH 6.5가 되는 노즐 직경을 예측하는 상관식을 제안하였다.
Abstract
In this study, numerical analysis was conducted for designing nozzle diameters to recover the pH value of scrubber wash-water of ships in accordance with the IMO (International Maritime Organization) regulation. It is prescribed that the scrubber wash-water should attain a minimum pH value of 6.5 at a distance of 4 m from the discharge point. By employing theoretical acid-alkali chemical reactions, titration curves were obtained, and the dilution ratio and volume fraction were calculated at the pH value of 6.5. Subsequently, CFD diffusion analysis was conducted for calculating the volume fraction with respect to various discharge velocities and nozzle diameters. The obtained analysis results indicated that the discharge velocity marginally affected the diffusion process, whereas the nozzle diameter significantly affected the diffusion process. Furthermore, based on numerical results, a correlation was developed according to the dilution ratio for predicting the nozzle diameter required for attaining a pH value of 6.5 at a distance of 4 m from the discharge point.
Keywords:
Computational fluid dynamics (CFD), Dilution ratio, International maritime organization (IMO), Nozzle, Scrubber, Wash-water키워드:
전산유체역학, 희석비, IMO, 노즐, 스크러버, 세정수1. 서 론
IMO(International Marine Organization)는 2020년 1월 1일부터 ECA(Emission Control Area)외의 전 해역에서 선박 연료유의 황 함유량을 기존 3.5%에서 0.5%로 강화하기로 결정하였다[1]. 이에 따른 대응으로는 첫 번째, 저유황유를 사용하는 방안, 두 번째, 스크러버(scrubber) 등과 같은 후처리 장치를 설치하는 방안, 그리고 마지막으로는 LNG와 같은 대체 연료를 사용하는 방안이 제기되었다[2][3]. 그리고 국내 대형 선사인 현대상선은 황산화물 배출 규제에 대응하기 위해서 스크러버 장착을 선택하였다. 선령이 오래된 선박의 경우 저유황유를 사용하는 것이 경제적이나, 4년 이상의 사용기간을 고려한다면 스크러버의 사용이 경제적인 것으로 분석되고 있다[4].
선박용 스크러버는 세정수 배출 방법에 따라서 open loop system, closed loop system 그리고 hybrid scrubber system 으로 구분되며, 그 중 open loop system은 해수를 스크러버 내부로 통과하는 배기가스에 직접 분사하여 황산화물을 제거하고 세정수는 pH 농도 및 배출 규정에 따라서 선외로 배출하게 된다.
Bell and Nebeker et al. [5]의 연구에 따르면 대부분의 해양생물들은 pH 5 의 환경에서 96시간 생존가능하나, pH 3 이하에서 생존율은 급격하게 감소한다. 따라서 IMO에서는 선박이 정지해 있을 경우, 스크러버 세정수는 배출지점으로 4m 에서 pH 6.5 이상이 되어야 한다고 규정하고 있다[6]. 이는 실험을 통해서 입증하거나 수치해석적 방법을 포함한 다른 동등한 과학적으로 입증된 방법을 사용하여 선급의 인증을 받아야 한다.
H. Ulpre et al. [7]은 화학 반응 모델을 기반으로 유체 유동에 대한 모델을 결합하였으며, 이론적인 방법을 토대로 염기성 환경에 주입된 산성 난류 제트의 산 농도의 변화를 실험을 통하여 입증하였다. 그리고 이를 기반으로 후속 연구[8]로서 세정수 배출을 위한 노즐 직경 사이즈와 개수 산정을 위한 연구를 수행하였다.
본 연구의 연구절차는 우선 H. Ulpre et al. [7][8]의 연구에서 사용한 화학 반응 모델을 토대로 적정 곡선을 그리고 이에 따른 스크러버 배출수와 해수의 희석비를 확인하고, 이 희석비를 확인하기 위해서 노즐직경과 배출속도를 변수로 확산해석을 수행하였다.
본 연구에서는 선박의 스크러버 세정수 배출 규정과 IMO에서 제시한 가이드 라인 및 관련 기존의 연구를 분석하고, 이를 기반으로 CFD를 이용한 수치해석적 방법을 접목하여 선박 스크러버 배출을 위한 노즐 직경을 설계하는 절차를 소개하였다. 또한 CFD 계산 결과를 기반으로 스크러버 배출수 규정인 4m이내에서 pH 6.5 회복을 위한 노즐 직경을 산출하는 상관식을 제안하였다.
2. 화학 반응 모델링
Bronsted-Lowry의 정의에 따르면, 산과 염기는 각각 수소 이온을 줄 수 있는 물질과 수소 이온을 받을 수 있는 물질로 정의하며, 주로 식 (1) 과 같이 pH로서 표현된다.
| (1) |
본 연구에서는 H. Ulpre et al. [7]의 산-약염기 반응을 기반으로 모델링하였다. 해수는 약염기 완충 용액(buffer solution)으로서, 완충용액은 산이 약간 첨가 되어도 수소이온을 흡수함으로써 pH 변화가 거의 일어나지 않는 용액을 의미한다. 해수의 완충 용량은 주로 와 이온에 의해서 결정된다[9].
다음과 같이 산 HA와 염기 MOH의 화학적 평형식에 의해서 표현된다.
| (2) |
이 때 산(a)과 염기(b)의 질량은 식 (3), (4)와 같이 보존된다.
| (3) |
| (4) |
여기서 대괄호 [ ]는 몰농도(mol/l)를 의미하며, Ca는 a의 농도, Va는 a의 체적을 나타낸다. 식 (2)를 식 (3)에 대입하게 되면 다음과 같이 [A-]를 소거할 수 있다.
| (5) |
그리고 [M+]를 소거하기 위해서 식 (5)를 식 (4)에 대입하면 식 (6)과 같이 나타낼 수 있으며, 식 (6)은 식 (7)과 같이 Va와 Vb에 대해서 풀어서 표현할 수 있다.
| (6) |
| (7) |
물, 산 그리고 염기의 이온화 상수는 각각 다음과 같이 정의 된다.
| (8) |
| (9) |
| (10) |
식 (4)를 [MOH](Va+Vb)의 항으로 정리하고 식 (10)을 이용하면 다음과 같이 주어진다.
| (11) |
식 (11)을 식 (7)에 대입하고 [OH-]를 Kw/[H+]로 치환하면 다음과 같이 산성-염기성 표준 적정식(standard acid-alkali titration equation)이 유도된다.
| (12) |
여기서, S는 Vb와 Va의 비인 희석비(dilution ratio)를 의미한다.
그리고 약염기 반응에서는 Kw/[H+]>>Kb 이므로 다음과 같이 나타낼 수 있다 [7].
| (13) |
또한 이양성자성 산(diprotic acid)의 경우 희석비는 다음 식과 같이 표현 가능하다.
| (14) |
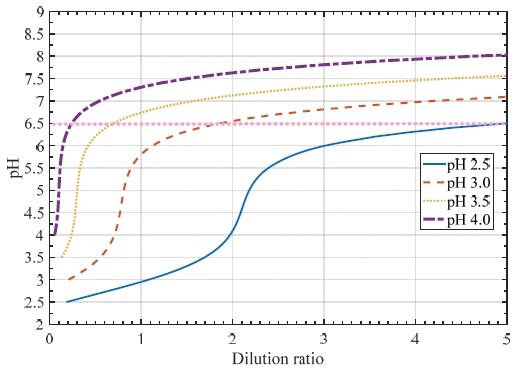
Figure 1은 식 (13)을 희석비에 따른 pH 를 나타낸 것이다. 이때, 해수의 알칼리도는 2,200 μmol/kg 로 가정하였으며, 산성의 배출수는 초기값 pH 2.5, 3.0, 3.5 그리고 4.0 으로 가정하였다. 스크러버 배출수는 4m에서 pH 6.5 이상의 값을 가져야 하므로, 각 초기 pH에 대해서 pH 6.5일 때의 희석비는 Table 1과 같다.
3. 수치해석 모델링
앞서 2장에서 수행한 화학반응 모델링을 토대로 얻어진 적정곡선을 통해서 세정수와 해수의 희석비에 따른 pH 값을 계산할 수 있으므로, 본 장의 수치해석에서는 화학반응을 고려하지 않고 확산해석을 통해서 희석비를 계산하고자 한다.
본 연구에서는 세정수가 해수 중에 분사되어 확산되는 과정을 CFD를 이용하여 분석하였다. 이때, 세정수와 해수와의 화학반응은 물리적인 혼합과정에 비해서 매우 짧은 시간(10-8s)에 의해서 이루어지는 것으로 가정하여 [10], 수치해석에서는 화학반응을 다루지 않았다. 그리고 세정수의 구성비는 대부분 해수이므로, 해수로 가정하였다.
세정수가 해수 중에 확산되어 가는 과정을 모사하기 위해서 체적 분율을 식 (15)와 같이 수송방정식(transport equations)에 적용하여 풀었으며 [11], 수치해석을 위해서 상용코드인 ANSYS CFX V17.0 을 이용하였다.
| (15) |
여기서 ρ는 밀도, U는 속도, ϕ는 체적 분율, Dϕ는 확산계수 그리고 Sϕ는 소스항을 나타낸다.
3.1 해석조건
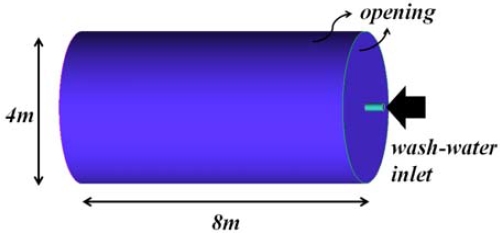
수치해석을 위한 유동 도메인의 형상은 Figure 2에 나타내었다. 전체 도메인은 직경 4m, 길이 8m로 설정하였다. 제트 전체의 유동을 확인하기 위해서는 8m 보다 더 긴 도메인이 필요하나 본 연구에서는 4m까지의 체적 분율을 확인하는 것이 목적이므로 8m 길이를 설정하였다. 노즐에서 분사되는 조건으로는 0.5 ~ 2.5 m/s의 속도 조건을 사용하였으며, 전체 도메인의 외부는 opening 조건을 사용하였다. 노즐 직경은 50 ~ 300 mm 를 적용하였다.
본 연구에서 사용한 난류모델은 k-ϵ 이며, 본 난류모델의 경우 벽함수를 사용하여 경계층에서의 값을 예측한다. 그리고 k-ϵ 모델의 경우 벽면에서 첫 번째 격자까지의 무차원 거리를 나타내는 y+ 값은 30이상 300이하의 값을 사용하는 것이 권고된다.
3.2 격자 의존성 검토
본 연구에서는 수치해석을 위한 격자 생성을 위해서 ANSYS ICEM-CFD 17.1을 이용하여 Hexa 격자계로 구성하였다. ICEM-CFD의 O-grid 기법을 활용하여 격자를 생성하였으며, 속도 및 수송변수의 구배가 클 것으로 예상되는 영역에서는 조밀한 격자계를 구성하였다. 수치해석적 방법의 격자 의존성을 검토하기 위해서 노즐 직경 200mm, 분사 속도 2 m/s에 대해서 노드 수 약 20만개, 50만개, 100만개, 200만개로 구성하여 격자 의존성 검토를 수행하였다.
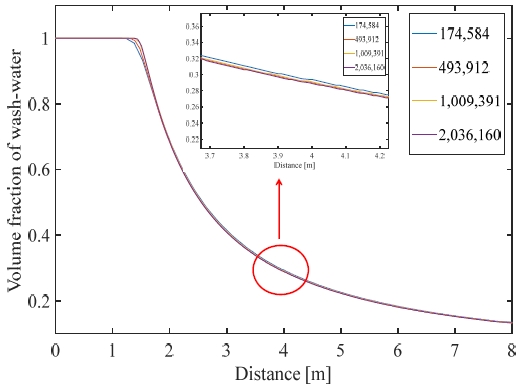
각 노드수에 대한 제트 분사 거리에 따른 체적 분율을 Figure 3에 나타내었다. 노드수 약 50만개 이상의 격자에서 거리에 따른 체적 분율의 변화 추이는 거의 일치하였다. 다만 분사된 세정수가 1~2m 거리에서 확산이 급격하게 이루어지는 지점이 노드 수에 따라서 차이가 발생하였으므로 세정수가 분사되는 지점에 보다 조밀한 격자를 구성할 필요가 있다. 따라서 최종적으로 Figure 4와 같이 노즐직경 200mm 기준 노드수 약 75만개의 Hexa 격자계로 구성하였다. 본 연구에서 사용한 격자계에서 y+ 값은 약 40 정도로 계산된다.
4. 결과 및 고찰
4.1 배출 속도에 따른 확산
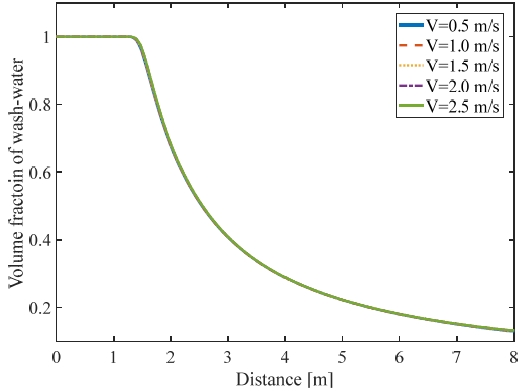
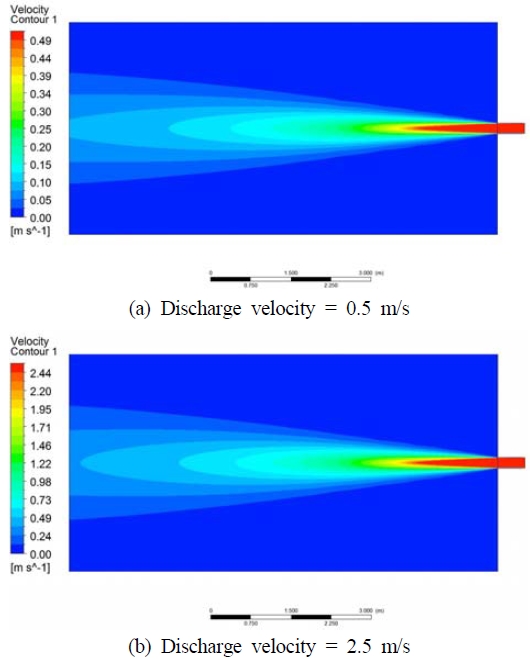
Figure 5는 세정수 배출속도 0.5 ~ 2.5 m/s에서 분사지점으로부터 유동 진행거리에 따른 세정수의 체적 분율을 나타낸 것이다. 결과에 의하면 배출 속도는 확산에 거의 영향을 미치지 않는 것으로 나타났다. 만약 배출 속도가 층류영역에 해당 될 정도로 낮다면 점성력의 영향이 증가하여 다른 형태의 유동이 나타날 것으로 예상된다. 하지만 본 연구에서 수행한 유동 해석의 속도 조건은 Reynolds number 약 100,000 ~ 500,000 범위의 난류 영역에 해당된다. 난류 제트에 의한 확산은 난류 제트의 속도와 확산에 의해서 주변의 유체가 유입되어 확산되는데 이때, 빠른 속도의 난류 제트는 Figure 6에서 보는 바와 같이 주변 유체의 유입 속도 역시 증가시키므로 결국 난류 제트에서의 속도는 확산에 크게 영향을 미치지 않는 것으로 판단된다.
4.2 노즐 직경에 따른 확산
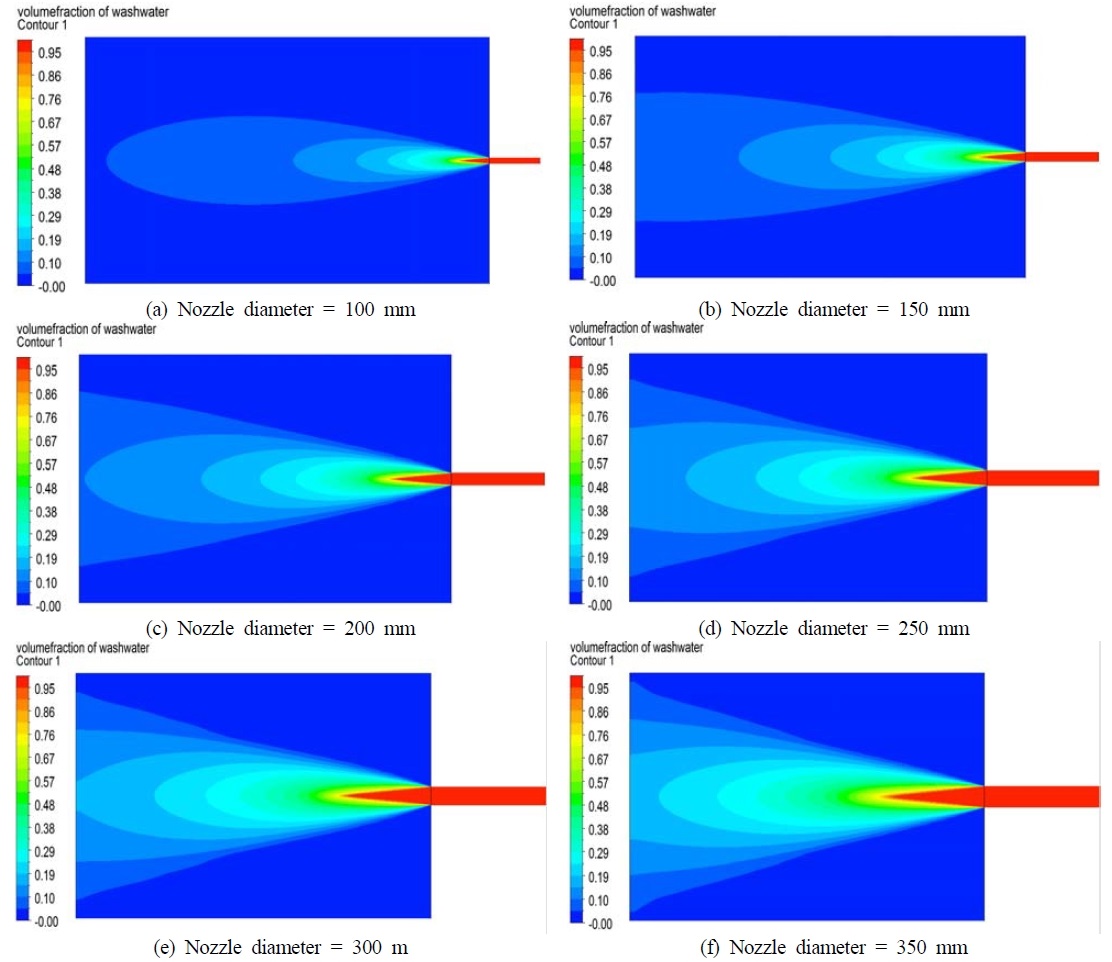
Figure 7은 노즐 직경 변화에 따른 세정수의 체적 분율 분포를 나타낸 것이다. 노즐 직경이 증가할수록 체적 분율 0.95이상의 세정수 유동의 거리가 길어지며, 이것은 곧 세정수의 희석이 잘 이루어지지 않음을 의미한다.
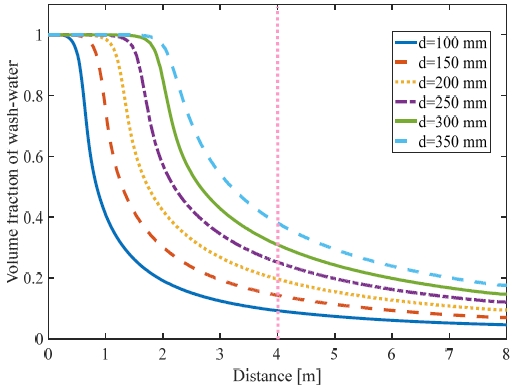
Figure 8은 노즐 직경 100 ~ 350 mm 에 따라서 진행거리와 세정수의 체적 분율을 나타낸 것이다. 앞서 살펴본 바와 같이 노즐 직경이 작을수록 확산의 시작 지점이 당겨지며, 확산이 시작되고 급격한 확산이 이루어지는 것으로 나타났다. 4m 지점에서의 노즐 직경에 따른 체적 분율은 Table 2에서 정리하였다.
4.3 노즐 직경 산출을 위한 상관식
스크러버 시스템을 설계하고 규정에 의거 선급 승인을 득하기 위해서는 세정수가 배출되어 4m 이내에서 pH 6.5 이상이 되도록 세정수 배출 노즐의 직경을 결정하여야 한다. 따라서 본 연구에서 수행한 수치해석 결과를 토대로 노즐 직경을 예측할 수 있는 상관식을 제안하고자 한다.
기존의 난류 제트 유동에서 거리에 따른 희석비를 예측하기 위해 사용하는 상관식은 Pani et al. [12]이 제안한 식과 이를 수정한 Ulpre and Eames [8] 상관식이 있으며, 이 식들을 4m 지점에서 희석비에 따른 직경을 계산하면 각각 다음과 같다. 그리고 다음의 식들은 4m 지점을 기준으로 0.267m 이하의 직경에 대해서 유효한 것으로 알려져 있다 [8][12].
| (16) |
| (17) |
여기서 d는 4m에서 희석비 S를 얻기 위한 노즐 직경[m] 이다.
본 연구에서는 수치해석 결과를 토대로 다음과 같은 식을 제안한다.
| (18) |
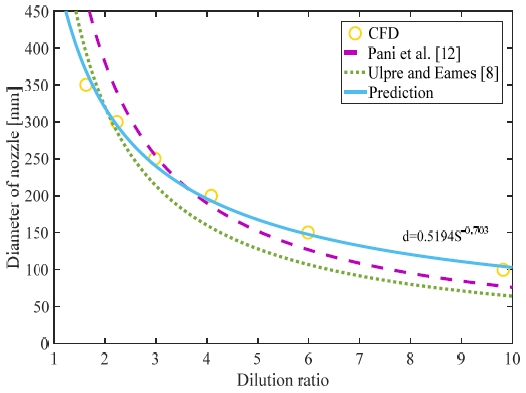
Figure 9는 수치해석 결과에 대해서 기존의 상관식과 본 연구에서 제안하는 상관식을 비교하여 나타낸 것이다. Figure 9에서 나타낸 바와 같이 기존의 상관식과 본 연구에서 제안하는 상관식의 경우 3이상의 희석비에서는 유사한 경향으로 희석비에 따른 노즐직경을 예측하였으나, 3이하의 희석비에서는 본 연구에서 제안하는 상관식에 의한 노즐의 직경이 더 작은 것으로 나타났다. 3이하의 희석비에서의 노즐 직경이 약 250mm 이상임을 감안하면, 3이하의 희석비에서의 노즐 직경예측은 기존의 상관식으로는 정확하게 예측할 수 없다. 작은 노즐 직경이 희석에 유리하다는 점에서 희석비 3이하, 그리고 노즐직경 250mm 이상의 경우 본 연구에서 제안하는 상관식이 기존의 상관식에 비해서 희석에 유리한 조건에 해당되므로, 기존의 상관식을 대신하여 사용하여도 무방할 것으로 사료된다.
본 연구에서 사용한 적정 곡선과 식 (18)에 따른 세정수의 초기 pH에 따른 노즐 직경은 Table 3과 같이 정리하여 나타내었다. 식 (18)의 계산에 의한 노즐 직경은 노즐 직경 100 ~ 350 mm 의 수치해석 결과에 기반하여 도출되었으므로, 350 mm 이하의 노즐 직경에 대해서 유효하다. 그리고 실제 선박에 적용 시 설치 등 현장 조건을 고려하여 초기 pH 3.5 이상의 경우 350 mm 의 노즐을 사용하는 것이 적절할 것으로 판단된다.
5. 결 론
본 연구에서는 선박 스크러버 세정수 배출 규제에 따라서 4m에서 pH 6.5 회복을 위한 세정수의 확산 해석을 수행하였으며, 이론적 화학반응에 근거하여 희석비를 확인하였다. 그리고 다음과 같은 결론을 얻었다.
- (1) 본 연구에서 수행한 세정수의 배출 속도 범위는 0.5 ~ 2.5m/s로서 Reynolds number 약 100,000 ~ 500,000 범위의 난류 영역에 해당된다. 속도가 증가함에 따라서 주변 유체가 난류 제트에 유입되는 속도 역시 증가하므로 배출 속도는 희석에 영향을 거의 미치지 않는 것으로 나타났다.
- (2) 노즐의 직경이 감소할수록 배출지점으로부터 짧은 거리에서 확산이 시작된다. 그리고 확산이 시작되면, 급격한 확산이 이루어지는 것으로 나타났다. 따라서 4 m 지점에서 높은 희석비가 요구될 때는 작은 직경의 노즐이 사용되어야 한다.
- (3) 기존의 상관식들 [8][12]은 267 mm 이하의 노즐 직경을 예측하는데 유효하므로, 수치해석 결과를 바탕으로 낮은 희석비에서도 노즐 직경을 예측할 수 있는 새로운 상관식을 제안하였으며, 본 상관식은 350 mm 이하의 노즐 직경을 예측하는데 유효하다. 본 상관식에 의해 계산된 노즐 직경은 약 250 mm ~ 350 mm 범위에서 기존의 상관식에 비해서 노즐 직경을 작게 예측하고 있다. 이것은 희석에 보다 유리한 조건에 해당하므로 기존의 상관식을 대신하여 사용하여도 무방할 것으로 사료된다.
Acknowledgments
Author Contributions
Conceptualization, Y. S. Choi, M. Kim and T. W. Lim; Methodology, Y. S. Choi and M. H. Cha; Software, Y. S. Choi and M. H. Cha; Validation, Y. S. Choi; Formal Analysis, Y. S. Choi and T. W. Lim; Investigation, M. H. Cha and M. Kim; Resources, Y. S. Choi and M. Kim; Data Curation, Y. S. Choi; Writing—Original Draft Preparation, Y. S. Choi; Writing—Review & Editing, M. Kim and T. W. Lim; Visualization, Y. S. Choi and T. W. Lim; Supervision, T. W. Lim; Project Administration, T. W. Lim; Funding Acquisition, T. W. Lim.
References
- IMO, MEPC 70/18/Add.1 ANNEX6, “Effective date of implementation of the fuel oil standard in regulation 14.1.3 of MARPOL ANNEX VI”, (2016), http://www.imo.org Accessed Jan. 23, 2019.
-
A. Armellini, S. Daniotti, P. Pinamonti, and M. Reini, “Evaluation of gas turbines as alternative energy production systems for a large cruise ship to meet new maritime regulations”, Applied Energy, 211, p306-317, (2018).
[https://doi.org/10.1016/j.apenergy.2017.11.057]

-
A. Halff, L. Younes, and T. Boersma, “The likely implications of the new IMO standards on the shipping industry”, Energy Policy, 126, p227-286, (2019).
[https://doi.org/10.1016/j.enpol.2018.11.033]

- L. Jiang, J. Kronbak, and L. P. Christensen, “The costs and benefits of sulphur reduction measures: Sulphur scrubbers versus marine gas oil”, Transportation Research Part D: Transport and Environment, 24, p19-27, (2014).
- H. L. Bell, and A. V. Nebeker, “Preliminary studies on the tolerance of aquatic insects to low pH”, Journal of the Kansan Entomological Society, 42(2), p230-236, (1969).
- IMO, Res. MEPC. 259(68), Exhaust Gas Cleaning System Guidelines, (2015).
- H. Ulpre, I. Eames, and A. Greig, “Turbulent acidic jets and plumes injected into an alkaline environment”, Journal of Fluid Mechanics, 734, p253-274, (2013).
- H. Ulpre, and I. Eames, “Environmental policy constraints for acidic exhaust gas scrubber discharges from ships”, Marine Pollution Bulletin, 88(1-2), p292-301, (2014).
-
T. G. Thompson, and R. U. Bonnar, “The buffer capacity of sea water”, Industrial and Engineering Chemistry Analytical Edition, 3(4), p393-395, (1931).
[https://doi.org/10.1021/ac50076a029]

-
M. Eigen, “Methods for investigation of ionic reactions in aqueous solutions with half-times as short as 10-9 sec. Application to neutralization and hydrolysis reactions”, Discussions of the Faraday Society, 17, p194-205, (1954).
[https://doi.org/10.1039/df9541700194]

- ANSYS CFX-Tutorials, V17.0., (2016).
- B. S. Pani, A. C. H. Lai, and C. K. C. Wong, “Turbulent jets: point-source and CFD simulation results”, Journal of Environmental Research and Development, 5(4), p952-959, (2011).