CFD 해석을 이용한 배관지지용 유압식 완충기의 밸브 스프링 설계 및 지지하중 평가

1. 서 론

유압식 완충기는 다양한 산업분야에서 다양한 형태로 쓰이고 있다. 대표적으로 차량의 스프링-댐퍼 서스펜션, 발전시스템 및 해양플랜트 배관지지 등이 있으며, 대부분의 경우 불특정한 외력이나 동하중에 대응하기 위해 사용되고 있다. 범용 완충기(Shock absorber)에 대한 연구개발은 활발히 수행되어 왔으나[1]-[4], 플랜트 배관지지용 유압식 완충기(Hydraulic snubber)에 대한 국내 연구개발은 아직 미흡한 수준이다. 현재 국내에서 건설되는 대부분의 플랜트에는 외국에서 수입된 유압식 완충기가 설치되고 있는 실정이다. 이는 배관지지용 유압식 완충기가 플랜트 구축에 필수적인 부품임에도 불구하고, 내부 형상이 복잡하며 외력이 작용할 때 부품의 움직임을 적절하게 반영해야 하므로 제품의 구조 설계가 까다롭기 때문이다. 특히, 유압식 완충기의 지지하중과 작동 성능을 결정하는 밸브의 설계에는 높은 기술력이 필요하다.

플랜트 배관지지에 사용되는 완충기는 일반적인 완충기와 같이 충격을 흡수하여 하중 차단하는 기능뿐만 아니라, 특수한 상황에서 하중을 그대로 구조물에 전달하는 기능이 요구된다[5]-[7]. 즉, 플랜트 기동 및 정지에 따른 진동과 열 변위와 같이 예견된 하중 또는 변위는 완충기에서 완전하게 흡수되어 배관이 구조물에 구속되지 않아야 한다. 그러나 지진과 같이 일상적인 범위를 벗어나는 큰 동하중이 작용하는 경우에는 배관을 구조물에 구속시켜 하중을 구조물에 전달하고 배관의 진동을 억제할 수 있어야 한다. 또한 일반적인 완충기에 비해 플랜트 배관지지용 완충기는 가혹한 진동하중 및 온도 조건 하에서도 안전한 작동이 보장되어야 한다. 따라서 완충기의 보수적인 설계를 위해서는 온도에 따른 유압유의 점도 변화를 충분히 고려해야 한다[8].

본 논문에서는 먼저 플랜트 배관지지용 완충기의 전체적인 구조와 가장 중요한 부품인 밸브의 작동원리를 파악한다. 이어서, 완충기 내 유압유 유로를 모델링하고 전산유체역학(Computational fluid dynamics; CFD) 해석을 수행함으로써 목표 성능을 달성하기 위한 밸브 스프링의 강성(Stiffness)과 지지 가능한 하중을 계산한다. 특히, 물성이 다른 두 가지의 유압유를 사용하고 각각 25℃, 100℃ 온도에서의 동점도를 반영함으로써 온도에 따른 유압유 특성의 영향을 고찰한다. 이를 통하여 배관지지용 유압식 완충기 설계에 대한 기초를 제공하고 국산화 개발에 기여하고자 한다.

2. 유압식 완충기의 구조 및 작동원리

플랜트 배관지지용 유압식 완충기는 작동 상태에 따라 내부의 유압유 유로가 달라진다. 이 장에서는 유압식 완충기의 전체적인 구조를 설명하고, 완충기의 인장/압축 시에 나타나는 제어밸브의 이동과 그에 따른 유동장 변화를 분석한다.

2.1 전체 구조 분석

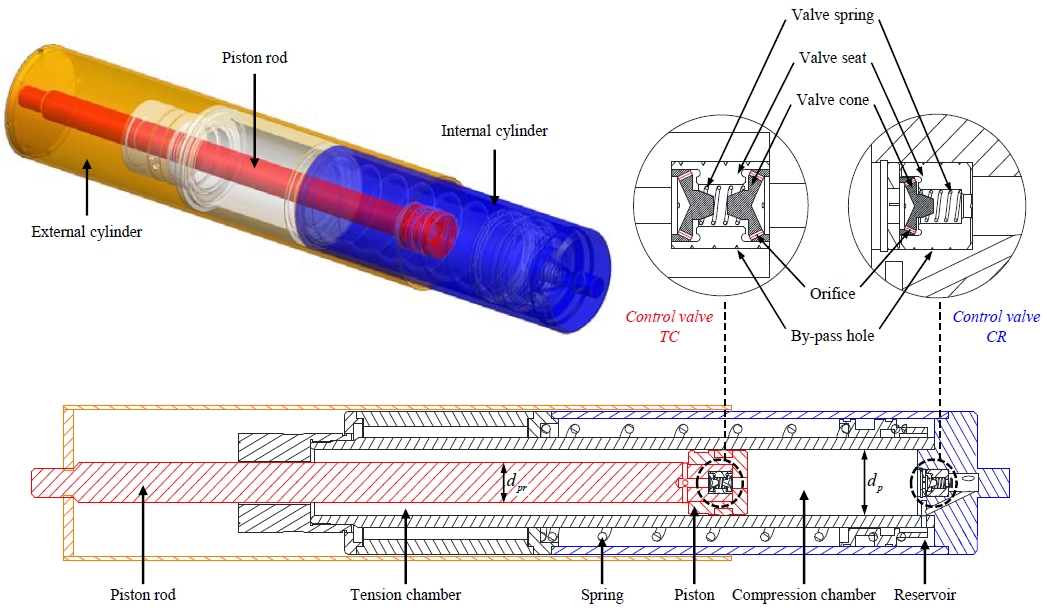
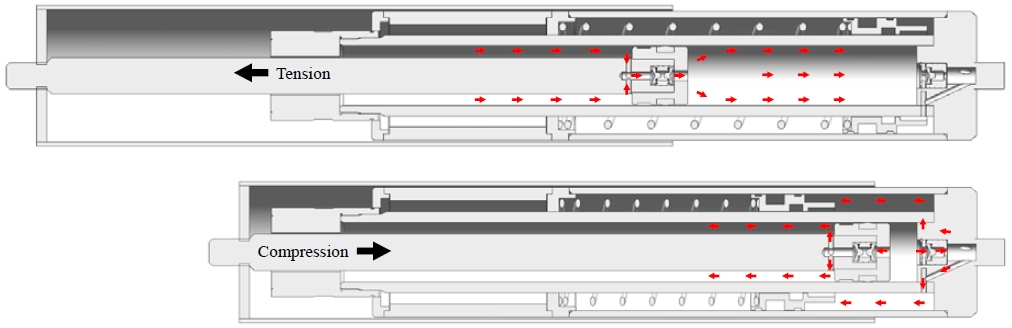
유압식 완충기의 작동원리를 파악하기 위해 먼저 전체적인 구조를 분석할 필요가 있다. Figure 1은 본 연구에서 다루고 있는 스프링-댐퍼 구조의 전형적인 유압식 완충기 내부를 나타낸다[5][6]. 대부분의 유압식 완충기에는 인장실(Tension chamber), 압축실(Compression chamber), 유압유 저장실(Reservoir)로 구성된 3개의 유압유 저장공간이 존재한다. 각각의 저장공간의 체적은 외력에 의한 피스톤 로드의 변위에 따라 달라진다. Figure 2는 완충기의 인장 및 압축 상태 각각에 대하여 전체적인 유압유의 유동을 도시한 것이다. 인장실과 압축실 사이(Figure 1에 제어밸브 TC로 표기)와 압축실과 저장실 사이(Figure 1에 제어밸브 CR로 표기)에 제어밸브가 각각 설치되어 완충기를 통한 하중 전달여부를 결정하게 된다. 압축 상태에서 저장실로 들어온 유압유는 내부 실린더에 장착된 스프링을 압축하게 되면서 유압식 완충기는 스프링-댐퍼 기능을 한다.

Figure 1:

Internal structures of a hydraulic snubber

Figure 2:

Hydraulic oil flow inside the hydraulic snubber subjected to tensile and compressive loads

2.2 완충기 인장/압축 상태에서의 제어밸브 거동

피스톤 내부(제어밸브 TC)에는 Figure 1과 Figure 3 (a)에 확대하여 나타낸 것과 같이 오리피스가 포함된 밸브콘이 양방향으로 배치되어 하중 조건에 따라 인장실과 압축실 사이의 유량을 제어한다. 열변위 등으로 인해 완충기 내에서 피스톤이 서서히 이동하는 경우에는 밸브콘의 오리피스와 밸브시트에 형성되어 있는 나선형의 우회유로를 통해서 유압유가 이동한다. 완충기에 인장하중이 작용하면 인장실(Figure 3 (a)의 왼쪽)에서 압축실(Figure 3 (a)의 오른쪽)로 유압유가 이동하며, 반대로 압축하중이 작용하면 압축실로부터 인장실로 유압유가 이동한다. 이때 밸브시트 전후에서 압력차이는 크지 않으며 압축된 스프링에 의해 밸브콘은 밸브시트와 이격된 상태를 유지한다.

Figure 3:

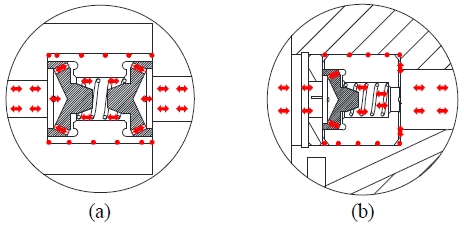
Flow paths in an unlock-up state of control valves: (a) between the tension and compression chambers and (b) between the compression chamber and reservoir

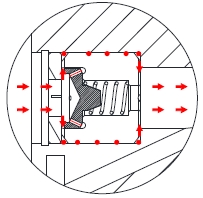
배관에 작용하는 외력에 의하여 피스톤의 이동속도가 증가하면 밸브콘의 오리피스를 통과하는 유압유의 유속은 급격히 증가하여 밸브시트 전후의 압력차이가 크게 발생한다. 피스톤의 이동속도가 설계기준 속도보다 큰 경우에는 압력차이의 의해 밸브콘에 작용하는 힘은 압축된 스프링이 밀어내는 힘과 밸브시트에 작용하는 마찰력의 합력보다 커지면서 밸브콘이 Figure 4와 같이 이동한다. 완충기의 인장 상태에서는 Figure 4 (a)와 같이 인장실 쪽의 밸브콘이 밸브시트에 닿게 되며, 압축 상태에서는 Figure 4 (b)와 같이 압축실 쪽의 밸브콘이 밸브시트에 닿으면서 오리피스를 통한 유동이 차단되고 나선형의 우회유로를 통해서만 유압유가 이동한다. 이와 같은 상태를 잠김(lock-up) 상태라고 부른다. 오리피스에 비해 우회유로는 단면적이 작고 유로 길이가 길기 때문에 큰 유동저항이 발생한다. 따라서 인장실과 압축실 사이의 큰 압력차이에 의해 피스톤은 저속으로 이동하게 되고 완충기는 강체처럼 작용하여 배관의 하중을 지지 구조물에 거의 그대로 전달하게 된다. 배관이 더 이상 이동하지 않는 경우에는 우회유로로 연결된 인장실과 압축실의 압력차이가 감소하여 밸브콘이 Figure 3 (a)의 풀림(unlock-up) 상태로 복귀하면서 오리피스를 통한 유압유 유동이 가능해진다.

Figure 4:

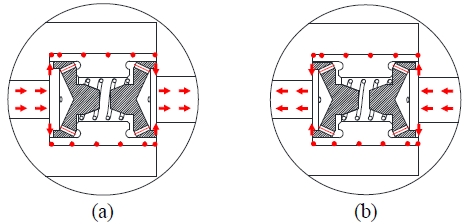
Flow paths in a lock-up state of a control valve between the tension and compression chambers: (a) under tensile loading and (b) under compressive loading

Figure 1의 오른쪽과 Figure 3 (b)와 같이 압축실과 저장실 사이(제어밸브 CR)에도 오리피스를 포함한 밸브콘이 설치되어 유압유의 유동 제어 역할을 한다. 인장실과 압축실 사이의 제어밸브 TC와 마찬가지로 설계기준 이하의 하중에서는 Figure 3 (b)와 같이 오리피스 및 우회유로를 통하여 유압유 유동이 발생한다. 그러나 압축실과 저장실 사이의 제어밸브 CR는 밸브콘이 단방향으로 설치되어 있으므로 인장 조건에서는 닫히지 않으며, 설계기준보다 큰 속도로 압축되는 경우에만 Figure 5와 같이 잠김 상태가 되어 우회유로를 통해서만 유동이 발생한다. 하중이 제거되면 저장실에 연결된 스프링에 의해서 밸브는 풀림 상태로 복귀하며 저장실과 압축실의 압력은 평형을 이루게 된다[6].

Figure 5:

Flow paths in a lock-up state of a control valve between the compression chamber and reservoir under compressive loading

3. CFD 해석 조건 및 결과

유압식 완충기의 내부 유동장에 대한 형상정보를 3D CAD로 모델링하고 상용 소프트웨어인 Star-CCM+를 이용하여 CFD 해석을 수행하였다. 실제의 유압식 완충기에서는 외력, 저장공간 사이의 차압, 밸브 스프링력, 밸브콘 마찰력, 저장실에 연결된 스프링력 등의 여러 인자들이 상호작용하여 동적 평형을 이루어 피스톤의 이동과 유체 유동을 결정하므로 엄밀한 해석을 위해서는 이러한 상호작용을 모두 반영해야 하지만, 이들을 모두 해석에 반영하는 것은 매우 까다로운 문제이다. 그러므로 본 연구에서는 두 개의 제어밸브 부분의 유동장만을 고려하고 정상상태 비압축성 층류 유동으로 CFD 해석 모델을 단순화하였다. 비록 단순화에 따른 근사가 도입되었지만 3장 및 4장에서 제시하고 있는 바와 같이 제어밸브의 잠김/풀림에 따른 유압유의 유동 경향 파악, 밸브 스프링 강성의 개략적인 설계 및 완충기 지지하중의 평가에는 무리가 없었다.

유압식 완충기가 인장/압축되면 피스톤이 이동하면서 피스톤의 속도로 인해 유압유의 유량 또는 유속이 결정된다. 따라서 Figure 6 (a)에 나타낸 바와 같이 인장실과 압축실 사이의 제어밸브 TC를 포함한 유동장에 피스톤의 이동 속도와 입구유속을 동일하게 부여하였다. 본 연구에서는 피스톤의 설계기준의 속도는 밸브의 잠김 직전에 3.20 mm/s, 인장시 잠김 상태에서 1.40 mm/s, 압축시 잠김 상태에서 1.05 mm/s로 설정하였다[5]. 즉, Figure 3 (a)와 같이 밸브가 열려있는 압축 상태에서는 잠김 직전 속도를 기준으로 압축실에 $$ v_{C\left(in\right)}^{comp,unlock}=3.20 \text{mm/s}$$의 입구유속를 부여하였으며 인장실에는 $$ p_{T\left(out\right)}^{comp,unlock}=0$$의 출구압력을 부여하였다. 반대로, Figure 3 (a)의 괄호 안에 나타낸 바와 같이 완충기의 인장 상태에서는 인장실에 $$ v_{T\left(in\right)}^{tens,unlock}=3.20 \text{mm/s}$$의 입구유속과 압축실에 $$ p_{C\left(out\right)}^{tens,unlock}=0$$의 출구압력을 부여하였다. 본 논문에서 압력(p), 압력차이(ΔP), 속도(v), 힘(F)을 나타내는 기호에 대한 두 개의 상첨자는 하중 조건(인장: tens, 압축: comp)과 밸브 개폐상태(잠김: lock, 풀림: unlock)를 각각 의미하며, 하첨자는 물리량이 정의된 위치(T: 인장실, C: 압축실, R: 저장실, TC: 인장실과 압축실 사이, CR: 압축실과 저장실 사이)를 의미한다. 유압유의 밀도와 동점도는 상온 25℃에서의 0.97g/cm³과 351mm²/s로 사용하였다.

Figure 6:

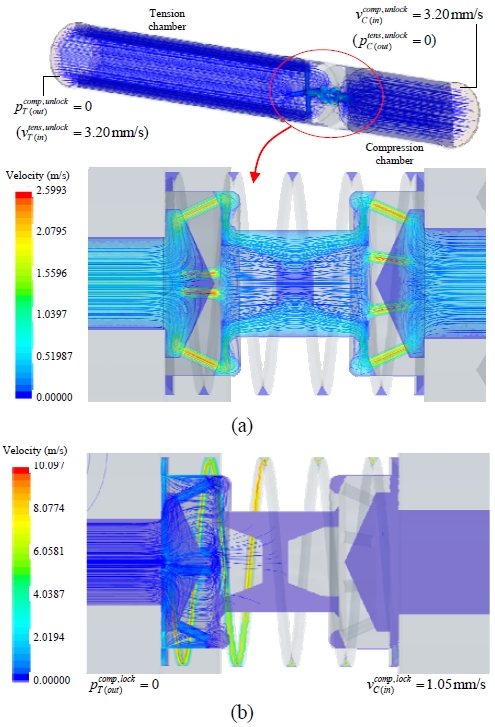
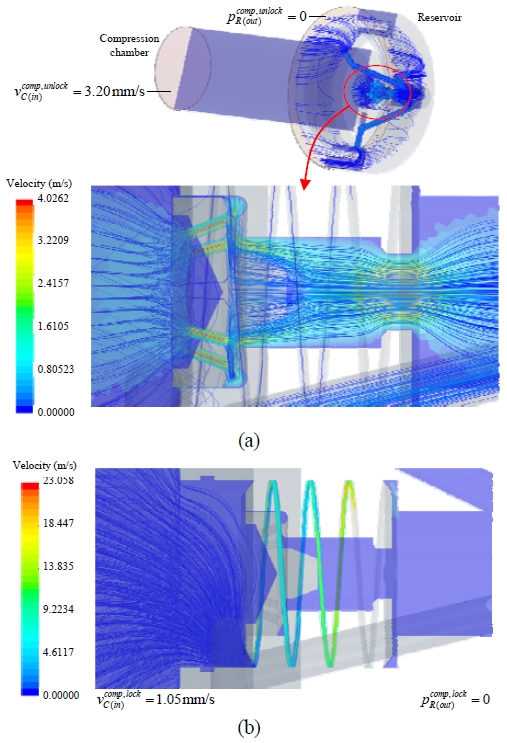
Velocity distribution through the control valve between the tension and compression chambers under compressive (or tensile) loading: (a) in an unlock-up state and (b) in a lock-up state

Figure 6 (a)은 피스톤이 압축될 때 인장실과 압축실 사이에서 열려있는 제어밸브 TC를 통과하는 유압유의 속도분포를 나타낸 것이다. 이때 대부분의 유압유는 밸브콘의 오리피스를 통과하며 우회유로를 통과하는 유량은 극히 적은 것을 알 수 있다. 또한 Figure 6 (b)은 제어밸브 TC가 잠김 상태로 피스톤이 압축될 때 압축실에 $$ v_{C\left(in\right)}^{comp,lock}=1.05 \text{mm/s}$$의 입구유속을 부여하여 얻은 속도분포이다. 이 경우에 모든 유동은 우회유로를 통해서 나타난다. 오리피스 단면적에 비해서 우회유로의 단면적이 작기 때문에 밸브의 풀림 상태에서 유속이 훨씬 큰 것을 확인할 수 있다. 피스톤이 인장되는 경우에도 마찬가지 방법으로 인장실에 입구유속 $$ v_{T\left(in\right)}^{tens,lock}=1.40 \text{mm/s}$$를 부여하여 유사한 경향을 관찰할 수 있었다.

압축실과 저장실 사이의 제어밸브 CR에 대한 해석결과는 Figure 7과 같다. 밸브콘은 완충기가 압축 상태일 때 단방향으로 작동하기 때문에 유압유가 압축실로부터 저장실로 흐르는 경우에 대해서만 해석을 수행하였다. Figure 3 (b)와 같이 밸브가 열려있는 경우에는 잠김 직전의 기준속도인 $$ v_{C\left(in\right)}^{comp,unlock}=3.20 \text{mm/s}$$을 입구유속으로 압축실 쪽에 부여하였으며, 저장실 쪽에는 출구압력 $$ p_{R\left(out\right)}^{comp,unlock}=0$$을 부여하였다. 이러한 조건으로부터 얻은 해석 결과는 Figure 7 (a)와 같다. 또한, 밸브가 잠김 상태가 되었을 때 입구유속을 $$ v_{C\left(in\right)}^{tens,lock}=1.05 \text{mm/s}$$로 부여하여 얻은 결과는 Figure 7 (b)와 같다. 인장실과 압축실 사이의 제어밸브 TC에 대한 해석결과와 마찬가지로 제어밸브 CR이 잠김 상태일 때 우회유로를 통과하는 유압유의 유속이 매우 빠른 것을 확인할 수 있다.

Figure 7:

Velocity distribution through the control valve between the compression chamber and reservoir under compressive loading: (a) in an unlock-up state and (b) in a lock-up state

4. 밸브 스프링 설계 및 지지하중 평가

앞서 언급한 바와 같이 유압식 완충기에서 여러 부품들의 거동은 외력에 따른 유압유 저장공간 사이의 압력 평형에 의해 비정상 상태를 거쳐 결정되므로 설계변수를 선정하고 목표 성능을 만족시키는 값을 결정하기 위해서는 상당한 경험과 기술력이 요구된다. 본 연구에서는 밸브 스프링의 강성을 설계 변수로 선정하고 CFD 해석을 통해 얻은 결과를 이용하여 밸브 스프링을 설계한다. 또한 CFD 해석의 결과인 압력차이를 이용하여 완충기가 지지할 수 있는 하중을 계산하였다. 또한 유압식 완충기의 작동 성능에 영향을 미치는 주요 환경요인 중 하나인 온도 조건을 고려함으로써 온도에 따른 동점도 변화를 반영하고 피스톤에 가해지는 힘을 분석하였다.

4.3 온도에 따른 유압식 완충기의 지지하중 평가

유압식 완충기는 유압유의 유동에 의해 작동되는데 유압유의 점도는 온도에 따라 변한다. 가혹한 온도 조건은 유압식 완충기의 성능저하 및 고장의 원인이 될 수 있으므로 온도에 따른 점도 변화를 고려하여 유압유를 적절히 선정해야 한다. 따라서 본 연구에서는 유압식 완충기에 대표적으로 사용되는 두 종류의 유압유에 대해서 25℃와 100℃에서의 점도를 반영하여 온도 또는 동점도 변화에 따른 지지하중을 평가하였다.

유압식 완충기의 압축 및 인장 지지하중의 계산 방법은 식 (6) 및 식 (7)에 나타낸 바와 같으며, 계산에 필요한 압력차이 $$ \Delta P_{TC}^{comp,lock}$$와 $$ \Delta P_{TC}^{tens,lock}$$는 압축실과 인장실 사이의 제어밸브 TC에 대한 CFD 해석으로부터 구할 수 있다. 유압유의 밀도는 25℃와 100℃에서 큰 차이가 없으므로 온도에 관계없이 동일한 값을 사용했으나, 동점도는 각각의 온도에서의 값으로 사용하였다. Oil-W 및 Oil-D로 표기한 두 종류의 유압유에 대해 밀도, 온도별 동점도, 압축 및 인장 지지하중은 Table 1에 정리된 것과 같다. 두 종류의 유압유를 사용했을 때 100℃에서의 지지하중은 25℃에서의 지지하중에 비해 각각 30%와 16% 수준으로 감소하는 것으로 나타났다. Oil-W는 큰 동점도로 인하여 더 큰 하중을 지지할 수 있으나 상대적으로 온도에 더 민감하므로 고온 작동환경에서 성능저하의 폭이 커지는 것을 알 수 있다.

Table 1:

Load-carrying capacity of the hydraulic snubber according to kinematic viscosity of hydraulic oil

5. 결 론

본 논문에서는 플랜트 배관지지용 유압식 완충기에 대한 구조 및 작동원리 분석을 바탕으로 제어밸브에 대한 CFD 해석을 수행하였다. 배관에 가해지는 하중 조건에 따라서 구조물에 가해지는 하중을 차단하거나 또는 구조물에 하중을 전달해야 하므로 제어밸브는 완충기의 핵심 부품이다. 유압식 완충기의 인장 또는 압축 상태에 따른 밸브의 이동을 고려하면서 밸브콘의 오리피스 및 밸브시트의 우회유로를 통과하는 유압유 유동에 대해 고찰하였으며 CFD 해석결과를 바탕으로 밸브 스프링의 강성을 결정하였다. 또한 가혹하게 높은 온도 조건에서 급격히 낮아지는 유압유의 동점도를 고려하면서 유압식 완충기의 인장 및 압축 지지하중을 평가하였다. 이를 통하여 완충기의 구조 설계와 유압유 선정에 대한 기초를 제공하고자 하였다. 향후에 유압유 저장공간 크기, 밸브콘 및 오리피스 형상, 스프링 강성 등 다양한 설계변수를 선정하고 가혹한 조건에서도 목표 성능을 만족시킬 수 있는 최적값을 도출하기 위해서 본 연구결과를 활용할 수 있을 것이다.

Acknowledgments

본 연구는 2017년도 산업통상자원부의 재원으로 한국에너지기술연구원(KETEP)의 지원을 받아 수행한 연구 과제(No.20171520000250)입니다.

References

• K. T. Park, and T. J. Park, “A CFD analysis of the oil flow in a hydraulic shock absorber”, Journal of the Korea Fluid Power Systems Society, 5(1), p20-26, (2008), (in Korean).
• S. Moon, and O. H. Kim, “Development of a shock absorber with an orifice sensitive to velocity”, Journal of the Korean Society of Manufacturing Technology Engineers, 22(3), p447-451, (2013), (in Korean). [https://doi.org/10.7735/ksmte.2013.22.3.447]
• J. W. Yun, “CFD analysis on the continuous and variable damping characteristics of a semi-active shock absorber”, Transactions of the Korean Society of Automotive Engineers, 12(2), p101-108, (2004), (in Korean).
• M. Shams, R. Ebrahimi, A. Raoufi, and B. J. Jafari, “CFD-FEA analysis of hydraulic shock absorber valve behavior”, International Journal of Automotive Technology, 8(5), p615-622, (2007).
• T. J. Park, C. H. Koo, G. H. Cho, D. R. Lee, H. Lee, and Y. H. Kim, “Development of hydraulic snubber for supporting the piping systems at power plants”, Proceedings of the 26th Korean Tribology Society Fall Conference, p232-238, (1997), (in Korean).
• J. C. Lee, M. H. Im, and T. Y. Hwang, “On the analysis of dynamic characteristics of pipe supporting hydraulic snubber in electric power plant with state-space model and impulse testing”, Journal of the Korean Society for Precision Engineering, 19(10), p130-138, (2002), (in Korean).
• M. Palmer, Finite Element Analysis of a Hydraulic Snubber with respect to Historical Test Data and American Society of Mechanical Engineers Requirements, M.S. Thesis, Department of Mechanical Engineering, University of Rhode Island, USA, (2015).
• J. H. Kim, S. M. Han, and Y. J. Kim, “Effects of viscosity of hydraulic oil on the performance of actuator”, The KSFM Journal of Fluid Machinery, 19(1), p31-36, (2016), (in Korean). [https://doi.org/10.5293/kfma.2016.19.1.031]
• J. Y. Park, S. H. Baek, and J. H. Kang, “Design criteria of spring stiffness for pan check valve using CFD analysis”, Journal of the Korean Society of Manufacturing Process Engineers, 13(3), p49-55, (2014), (in Korean). [https://doi.org/10.14775/ksmpe.2014.13.3.049]