
멤브레인형 LNG 화물창의 단열재에서 직사각형 밀폐공간 내에 자연대류 열전달에 관한 수치적 연구


Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
멤브레인형 LNG 화물창의 외벽에서 발생될 수 있는 결빙 현상을 이해하기 위해서, 단열재 내부에 냉온의 직사각형 밀폐공간 내에 자연대류 열전달과 상대습도의 상관관계를 대와동 모사를 이용하여 조사하였다. 등온 및 단열의 경계조건으로 단순화된 모델에서, 준-정상상태에 도달하였을 때에 대류열전달계수는 초기의 정지된 기체에 대한 것보다 약 2.5배까지 증가되었다. 대류열전달 특성에 대한 회귀분석의 결과를 바탕으로, 주어진 온도차에 의한 자연대류는 등온벽면 부근에서 우세하였지만, 유속의 크기에 따른 강제대류는 단열벽면 부근에서 더 우세하게 나타났다. 자연대류에 의한 열 및 유체의 유동에 따라, 가스온도가 이슬점 온도 아래로 떨어지는 경향은 LNG측 벽면 부근에서 대류열전달계수와 열유속이 상대적으로 낮은 지역에서 선호적으로 발생되는 것으로 확인되었다.
Abstract
To understand the icing phenomenon that may occur in the outer wall of a membrane-type LNG cargo containment system, the correlation between the natural convection heat transfer and relative humidity inside rectangular enclosures in the insulation was investigated by conducting a large eddy simulation. In simplified models with isothermal and adiabatic boundary conditions, the convective heat transfer coefficient was elevated to more than 2.5 times that of the initially stationary gas when the quasi-steady state was reached. Based on the results of a regression analysis of convective heat transfer characteristics, the natural convection owing to the given temperature difference prevailed in the vicinity of the isothermal wall surface. However, the forced convection as a function of the magnitude of flow velocity was dominant near the insulating wall surface. The results revealed that the tendency of the gas temperature to fall below the dew point temperature was preferentially generated in the region where the convective heat transfer coefficient and heat flux were relatively low near the LNG-side wall surface depending on the thermal and fluid flows as derived from the natural convection.
Keywords:
Natural convection, Heat transfer coefficient, Large eddy simulation, Rectangular enclosures, Membrane type LNG cargo containment system키워드:
자연대류, 열전달계수, 대와동모사, 직사각형 밀폐공간, 멤브레인형 LNG 화물창1. 서 론
2017년을 기준으로, 한국의 에너지 수입 의존도는 94 %로써 1,094.7억 달러에 달하며 수입된 에너지원 중에 천연가스가 차지하는 비율은 약 15.7 %이고, 이는 39.5 %의 석유 다음으로 두 번째로 높은 비율을 갖는다[1]. 천연가스는 주로 카타르, 호주, 오만, 말레이시아, 인도네시아 등에서 육상의 파이프라인 방식이 아닌 액화천연가스 (LNG) 운반선에 의해서 한국으로 수입되며, 세계적으로 일본과 중국 다음으로 많은 LNG 수입량을 차지한다[2]. 한국의 한해 총 LNG 수입량은 지난 십년 동안에 평균적으로 연간 약 4.5 %가 증가되었고, 2017년에는 37,537천 톤을 기록하였다[1].
국제적인 LNG 수요의 증가 추세에 따라, LNG 화물의 운반선에 대한 운송 효율을 향상시키기 위한 기술도 지속적으로 고도화되었다. 그 중에서도, 독립형 탱크보다 낮은 가스증발량과 높은 공간효율을 갖도록 GTT (Gaztransport & Technigaz)에 의해서 설계된 멤브레인형 LNG 화물창이 최근 LNG 운반선에 광범위하게 적용되고 있다[3]. Figure 1에 나타낸 개략도와 같이 LNG 운반선에서 멤브레인형 LNG 화물창은 인접한 선체구조에 의해서 지지되기 때문에, LNG 화물의 극저온으로 인해 낮아진 선체구조의 최저 온도분포에 대한 취성을 고려하여 강재의 등급 및 두께가 설계된다[4]. 강재의 온도가 허용온도 이하로 떨어지는 것을 방지하기 위해서, LNG와 선체 사이에 단열재 또는 가열부가 설치된다. 따라서, 저장탱크 외부에서 LNG로 유입되는 열유속을 최소화시키는 단열 방식 [5]은 가스증발량을 저감시키기 위한 LNG 운반선의 핵심기술 중에 하나가 될 수 있다.
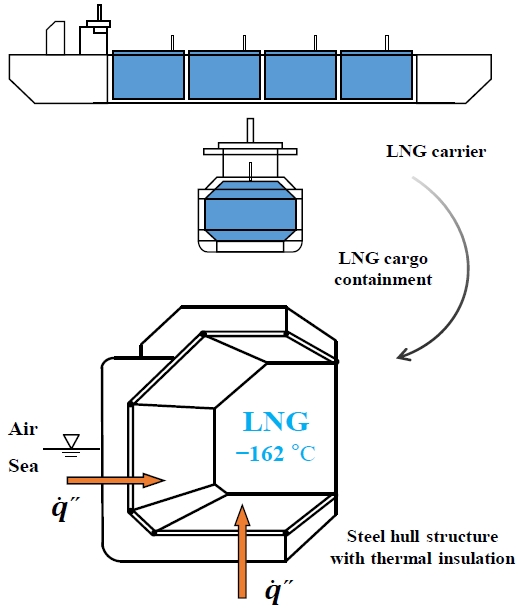
Schematic diagram of heat fluxes from sea to the insulated steel hull structure of a membrane LNG cargo containment
이와 관련된 열전달 해석에 관한 최근 연구로써, GTT의 LNG 화물창에 대한 단열 성능과 증발율의 수치적인 비교 연구가 수행된 바가 있고[6], 한국형 LNG 화물창에서 단열된 선체구조의 온도분포 및 증발율에 관한 수치해석적인 연구가 수행되었다[7]. 하지만, 부재의 상세한 형상뿐만 아니라 선체 주변의 대류열전달에 의한 영향들에 대한 보다 진보적인 해석의 필요성이 1997년에 이미 제기된 바가 있다[8]. 한편, 2004년부터 추진된 한국형 LNG 화물창의 기술개발의 결실로써, 2018년에 실제 선박에 탑재되어 운용되었지만, 화물창의 외벽에서 결빙 현상이 나타나서 운항이 정지된 것으로 알려졌다[9]. 이는 화물창 하부 가장자리에 위치한 단열재 내부의 작은 공간에서 발생되는 대류열전달의 영향에 의해서 발현될 수 있다는 가능성도 공개되었다[10].
단열재 내부는 일반적으로 유동이 없는 정지기체로 간주되고 있지만, 대류열전달에 대한 면밀한 검토가 요구된다. 또한, 대기 중에 습도와 과도 상태의 열적 영향이 간과되고 있는 실정이다. 따라서, LNG 화물창의 실제적인 선체구조에서 발생될 수 있는 대류열전달의 영향에 관한 체계적인 연구가 필요하다. 본 연구는 단열재 내부에 냉온 환경의 직사각형 밀폐공간 내에 자연대류 현상에 대한 이해를 증진하기 위해서, 수치해석적인 접근법을 채택하여 국부적인 대류열전달의 기초특성을 조사하였다.
2. 수치적 방법
대와동 모사에서 난류유동에 대한 순간적인 변수 Φ는 평균적인 요소 와 변동적인 요소 Φ″로써 와 같이 구성될 수 있다. 질량 가중화된 Favre 필터링은 와 같이 사용된다. 저역 통과 필터링으로 여과된 양 는 로 정의되고, 필터링 폭은 로 정의된다. 본 직사각형 밀폐공간의 내부 유동에 대한 대와동 모사에 있어서, 다음과 같은 Favre 필터링으로 여과된 지배방정식이 적용되었다[11]-[15].
질량보존:
| (1) |
운동량보존:
| (2) |
에너지보존:
| (3) |
화학종보존:
| (4) |
상태방정식:
| (5) |
여기서, ρ는 밀도, u는 속도벡터, p는 압력, τ는 점성응력텐서, sgs는 아격자 스케일, g는 중력가속도, hs는 혼합가스의 감지엔탈피, 는 열유속, Yi는 화학종 i의 질량분율, Ji는 화학종 i의 확산유속, R는 일반기체상수, T는 온도, 그리고 wi는 화학종 i의 분자량이다.
Figure 2은 본 연구에서 비교된 3 가지의 해석 모델에 대한 개략도를 나타내며, 중력 방향에 대한 상대적인 위치에 따라 (a) 수평의 Case A, (b) 수직의 Case B, 및 (c) 반-수직의 Case C로 구성된다. 초기 조건으로써, 해수 측의 벽면온도는 Touter = ‒20 ℃ 그리고 LNG측의 벽면온도는 Tinner = ‑100 ℃의 등온으로 가정하였다. 두 등온 조건 사이에 4개의 벽면은 열유속이 없는 단열 조건으로 고정하였다. 모든 벽면은 미끄럼 방지 조건으로 설정하였다. 그리고 내부에는 Tgas,0 = ‑60 ℃의 초기 온도에서 50 %의 상대 습도 (수증기의 체적분율: XH2O = 4.81E-6)를 갖는 불연성의 질소 (질소가스의 체적분율: XN2 = 1 ‑ XH2O)가 균질하게 채워진 것으로 가정하였다. 대표적으로 벽면과 내부의 기체 사이에 열적 경계조건은 다음의 관계식에 의해서 계산된다[11].
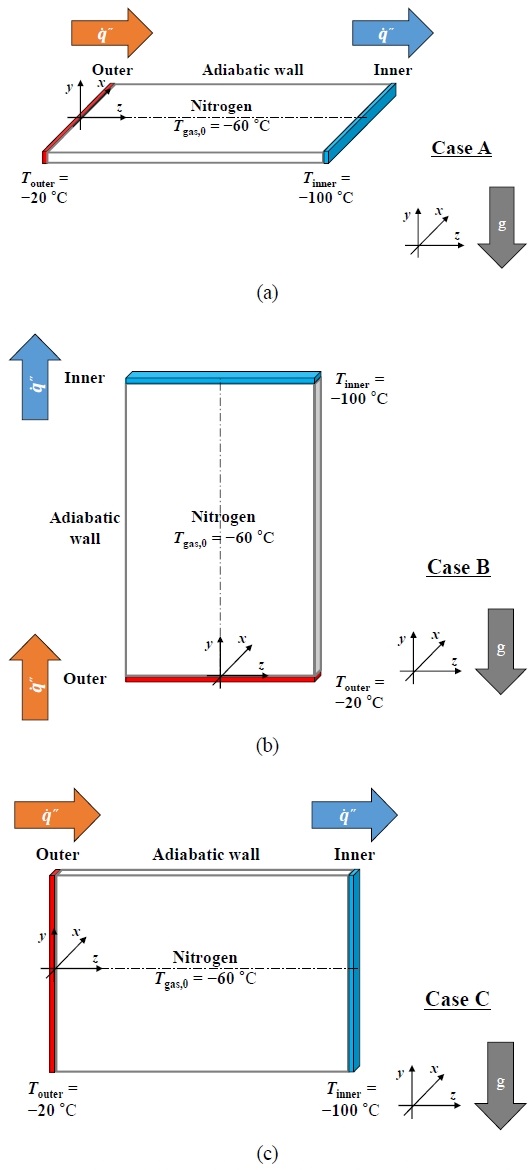
Simulated models for the enclosed spaces in the insulation of a membrane LNG cargo containment: (a) horizontal Case A, (b) vertical Case B, and (c) semi-vertical Case C
| (6) |
여기서 ks와 Ts는 각각 고체 표면의 열전도도와 온도이고, h는 대류열전달계수이다. 한편, 3-D의 계산 도메인은 x 방향으로 ± 1 m, y 방향으로 ± 0.1 m, z 방향으로 3 m의 크기를 갖고, 격자 민감도를 확인한 후에 0.02 × 0.02 × 0.02 m3의 일정한 격자로 총 150,000개가 선택되었다. 이전의 연구 [14][15]에서 사용된 소프트웨어를 동일하게 채택하였으며, 대와동 열유동 해석에 사용된 솔버는 Fire Dynamics Simulator [16]이고, Pyrosim [17]과 MATLAB [18]을 전처리 및 후처리에 각각 사용하였다. 아래에는 수평의 Case A, 수직의 Case B, 그리고 반-수직의 Case C에 대한 내부 열유동의 특성들이 직육면체의 중간 절단면에서 주로 비교되었다. 대표적인 물성치를 측정하는 지점으로써, 그 절단면의 왼쪽 아래의 모서리부터 왼쪽 변의 중간 지점을 포함하여 시계방향으로 총 6개의 가장자리들을 선정하였고, 이에 대한 좌표값들을 Table 1에 요약하였다.
3. 결과 및 토의
3.1 과도응답 특성
주어진 밀폐공간의 벽면온도에 의한 기체밀도 차의 부력으로 생성되는 내부 유동에 대하여, 대표적인 지점에서 대류열전달계수 h의 시간에 따른 과도응답 특성을 Figure 3에 나타내었다. 계산 초기의 모든 지점에서 약 h = 2을 갖는다. 우선 Figure 3 (a) Case A에서, 정지기체로부터 해수측 벽면 (Left)에 인접한 기체는 위로, LNG측 벽면 (Right)에 인접한 기체는 아래의 방향으로 밀도차에 의한 유체의 이동현상이 각각의 등온벽면에서 발생하였고, 이에 따라 양측의 등온벽면에서 h는 시간에 대하여 증가하다가 약 10s 후에 안정화되었다. 이때, h는 초기유동 방향의 반대지점인 Left-Down와 Right-Up에서 상대적으로 크게 증가되었으며, Left-Center와 Left-Center 그리고 Left-Up과 Right-Down의 순서로 h의 크기가 증가되었다. 위아래의 단열벽면을 따라 시계방향으로 이동하는 유동이 약 20s에서 단열벽면의 중간지점을 통과할 때, Center-up과 Center-Down에서 h는 각각 소폭으로 증가되거나 감소되었다. 유동은 약 40s에 이르러 1회 회전을 완료하게 되는데, 그 후로 좌우벽면에서 h의 크기가 더 증가하였고, 좌우의 등온벽면에서 시간에 따른 h의 변동은 약 100s 이후에 준-정상상태에 도달하였다.
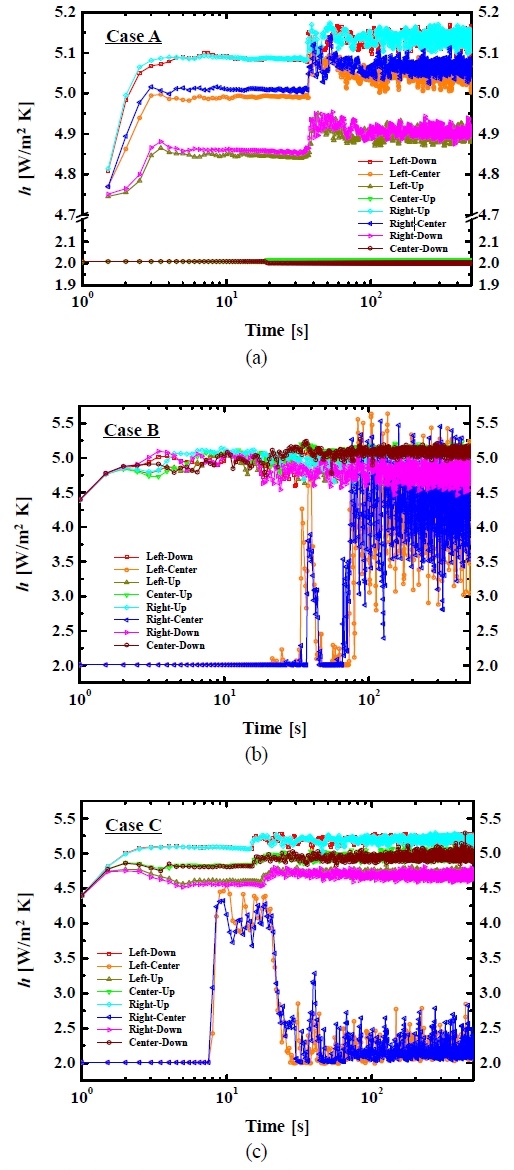
Transient response of convective heat transfer coefficients at the representative edge positions in the central plane of the enclosed spaces: (a) horizontal Case A, (b) vertical Case B, and (c) semi-vertical Case C
Figure 3 (b) Case B에서, 해수측 벽면 (Down)에 인접한 기체는 위의 방향으로 LNG측 벽면 (Up)에 인접한 기체는 아래의 방향으로 서로 대향하여 전체 공간으로 각각 이동하다가, 약 20s부터 중간 부근에서 혼합되기 시작하였다. 약 100s 이후로, 유동은 주로 측면의 단열벽면 주변을 따라 안정적으로 순환되는 경향을 보였다. 특히, Case (a)와 달리, 좌우의 단열벽면에서 h의 변동폭은 약 2.5-5.5로 크게 나타났다. Figure 3 (c)에서 Case C에 대한 시간에 따른 h의 변화는 Case A보다 더 빠른 응답과 안정화 특성을 보였다. 약 50s에서 안정화된 이후로, Case A에 대비하여, 등온벽면 (Left & Right)과 단열벽면 (Up & Down)에서 h의 변동폭은 각각 다소 증가되었다. 결과적으로, 각 Case A, B, 및 C에서 등온벽면의 온도차로 기인된 대류 현상이 일정한 환경 조건 하에서 최대로 약 100s 이상 유지될 때에 준-정상상태에 도달하는 것을 확인하였고, 이때 주어진 정치기체의 h 값을 기준으로 약 2.5배 이상 증가되는 것을 확인하였다.
3.2 준-정상상태의 내부 열유동
준-정상상태에서 내부 열유동의 특성들을 보다 자세히 조사하기 위해서, 총 500s의 계산시간에서 450-500s에 해당하는 50s 동안에 밀폐공간의 중간 절단면에 대한 물리량들을 평균하여 분석하였다. Figure 4은 수평의 Case A에 대한 중간 절단면에서 대표적인 열유동의 특성을 나타낸다. (a)에서 시계방향으로 순환되는 유선을 보이며, 순환되는 유선의 중심을 통과하는 w = 0를 갖는 등속도의 윤곽선은 좌우에서 유동방향으로 약간 편향되어 위치하였다. (b)에서 가스온도 Tgas는 w = 0의 윤곽선을 기준으로 상대적으로 높은 온도는 상부에, 상대적으로 낮은 온도는 하부에 분포되었다. 특히, 겹쳐진 속도벡터의 크기는 양 측면에서 데워져서 올라간 유동과 식혀져서 내려온 유동이 각각 중간을 향하여 이동될 때에 상대적으로 증대되었다. (c)에서 기체의 열전도도 k는 상대적으로 유동의 속도가 클 때, 약간 증가되는 경향을 보였다. (d)에서 기체의 상대습도 RH는 Tgas가 가장 낮은 영역인 우측 하부 (Right-Down)에서 상대적으로 높게 나타났고, RH > 100 %으로써 포화 수증기량을 초과하였다. 이는 Tgas가 우측 하부 (Right-Down)에서 이슬점 (Dew point) 온도 이하로 떨어졌기 때문에, 그 지역에 수증기가 응결되어 영하의 온도에 의해서 얼음이 성장될 수 있는 환경이 조성되었다는 것을 의미한다. 단, 수증기에서 액체로 응결되고 고체로 응고되거나, 삼중점 미만의 가스온도에서 고체로 승화되는 상변화 현상은 해석에서 제외되었다. 전반적으로, 절단면에서 열유동 특성은 w = 0를 갖는 등속도의 윤곽선을 중심으로 대각선 방향의 대칭적인 구조를 보였다.
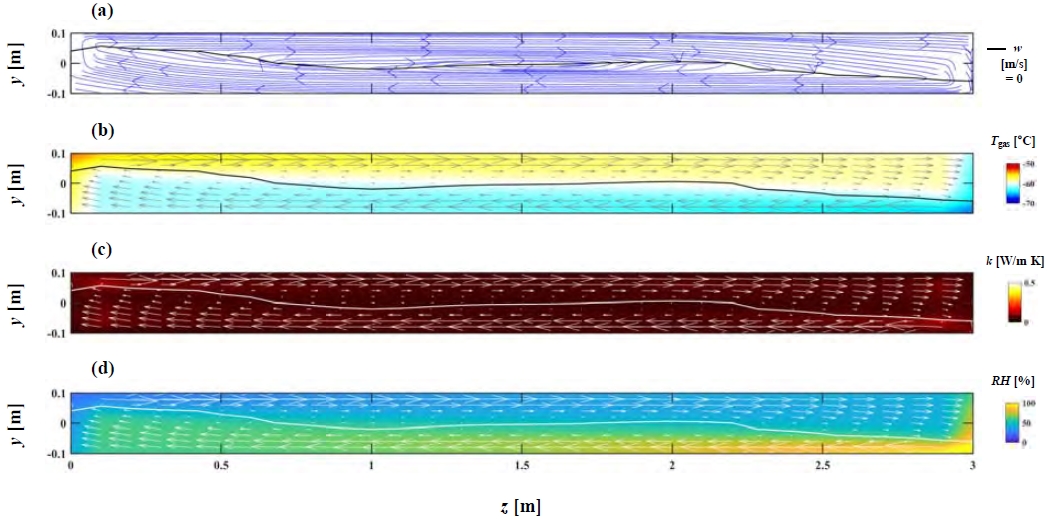
Time-averaged convective flow fields in the central z-y plane of horizontal Case A: (a) streamline with iso-velocity contour of w = 0, (b) gas temperature, (c) thermal conductivity of fluid, and (d) relative humidity, superimposed on the velocity vector field with the iso-velocity contour of w = 0.
Figure 5은 수직의 Case B에 대한 중간 절단면에서 대표적인 열유동의 특성을 나타낸다. (a)에서 시계방향으로 순환되는 유선은 반시계방향으로 순환되는 구조를 보였고, w = 0를 갖는 등속도의 윤곽선은 위아래로 길게 나타났다. ight-Up 및 Left-Down의 모퉁이에서 역방향으로 재순환되는 작은 영역이 나타났다. (b)에서 가스온도 Tgas는 w = 0의 윤곽선을 기준으로 우편에서 상대적으로 높은 온도로, 좌편에서 상대적으로 낮은 온도로 분포되었다. 특히, 겹쳐진 속도벡터의 크기는 작은 재순환 영역의 외각에서 상대적으로 증대되었다. (c)에서 기체의 열전도도 k는 마찬가지로 상대적으로 유동의 속도가 클 때에 증가되는 경향을 보였고, Figure 4 (c)에 대비하여 네 벽면에 근접한 부근에서 더 크게 증가하였다. 이는 수평의 Case A보다 수직의 Case B의 내부의 유속이 더 빠르다는 것을 암시한다. 일반적으로 대기압에서 정치기체의 온도가 감소하면 열전도도는 감소하는 특성을 보인다[19]. 그러나, 본 해석 조건에서 Figure 5 (b)의 가스의 온도와 Figure 5 (c)의 가스의 열전도도에 대한 분포를 비교해 볼 때, 열전도도의 변화는 유동에 의한 온도의 증감에 무관하게, 증가된 유속의 크기에 의해서 더 민감한 영향을 받는 것으로 나타났다. 이는 내부의 열전달 특성이 정지된 기체보다 자연대류 현상에 의해서 더 향상되었다는 것을 의미한다. 이에 대한 상세한 논의는 아래의 절에서 계속된다. (d)에서 기체의 상대습도 RH는 위쪽의 LNG측 등온 벽면에서 주류의 유속이 상대적으로 낮은 좌측 상부의 모퉁이 (Left-Up)와 재순환 영역 내에 저속의 지역인 우측 상부의 모퉁이 (Right-Up)에서 100 %를 초과하였다.
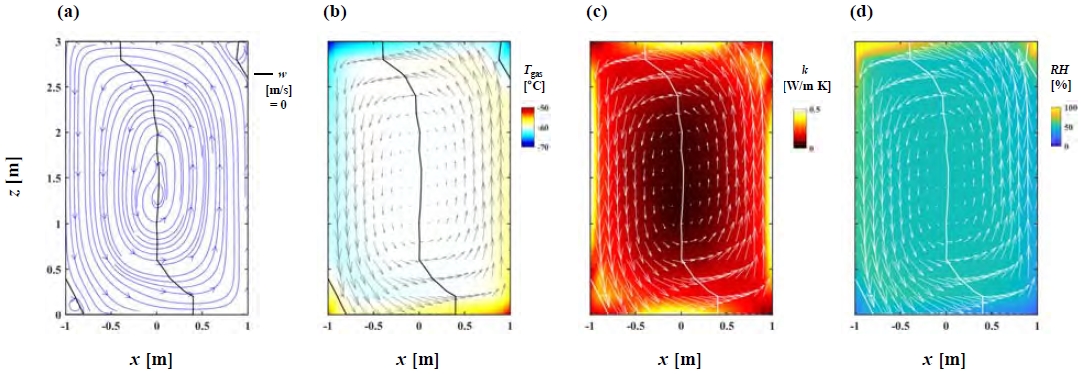
Time-averaged convective flow fields in the central x-z plane of vertical Case B: (a) streamline with iso-velocity contour of w = 0, (b) gas temperature, (c) thermal conductivity of fluid, and (d) relative humidity, superimposed on the velocity vector field with the iso-velocity contour of w = 0.
Figure 6은 반-수직의 Case C에 대한 중간 절단면에서 대표적인 열유동의 특성을 나타낸다. (a)에서 유선으로 나타낸 유동은 Case A 및 B와 같은 하나의 대규모 순환구조를 보이지 않았고, 시계방향으로 회전하는 재순환 영역이 단열벽면의 방향으로 상하부에서 두 군대로 분리되어 형성되었다. 두 재순환 영역 사이에는 w = 0의 윤곽선이 S자 모양으로 나타났다. (b)에서 가스온도 Tgas는 w = 0의 윤곽선을 기준으로 상대적으로 높은 온도는 위편에, 상대적으로 낮은 온도는 아래편에 분포되었다. 겹쳐진 속도벡터의 크기는 Figure 4 (b)와 유사하게 좌우의 등온벽면으로부터 각각 중간을 향하여 이동되는 영역에서 상대적으로 증대되었다. (c)에서 기체의 열전도도 k는 데워져서 올라가는 유동과 식혀져서 내려오는 유동이 위치하는 좌우의 등온벽면을 따라 상대적으로 더 크게 증가되는 경향을 보였다. (d)에서 저온영역이 분포하는 우측 하부 (Right-Down)에서 상대습도 RH가 높게 나타났으며, Case A 및 B에 대비하여 상대적으로 넓게 분포되었다.
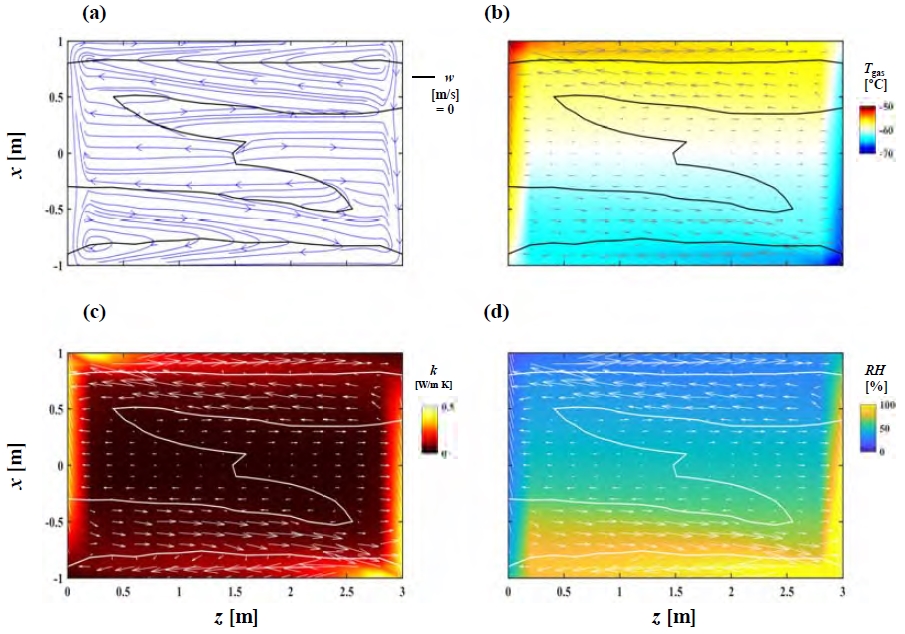
Time-averaged convective flow fields in the central x-z plane of semi-vertical Case C: (a) streamline with iso-velocity contour of w = 0, (b) gas temperature, (c) thermal conductivity of fluid, and (d) relative humidity, superimposed on the velocity vector field with the iso-velocity contour of w = 0.
3.3 자연대류 열전달과 상대습도의 연관성
준-정상상태에서 열전달 특성에 따른 상대습도의 연관성을 정량적으로 살펴보기 위해서, Table 1에 요약된 바와 같이, 중간 절단면에 대한 6개의 가장자리들에서 마지막 50s 동안에 평균된 물리량들을 비교하였다. 우선, Case A, B, 및 C에 대한 대표적인 가장자리에서 가스온도에 대한 상대습도의 값들을 Figure 7에 나타내었다. 내부의 상대습도는 아래의 식 (7)과 같이 가스온도의 역수에 대한 지수함수를 갖는 상관관계를 보였다.
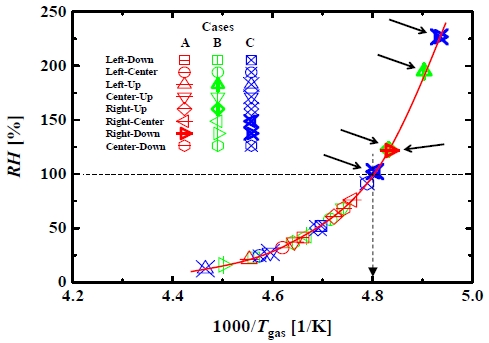
Relative humidities as a function of the inverse of gas temperatures: the arrows indicate local edge positions where symbols are located over the dashed line of RH = 100 %
| (7) |
이는 가스온도가 증가되면 포화 수증기량이 증가하기 때문에, Tgas의 변화에 따른 상대습도의 전형적인 성질과 동일하였다. 다시 말해서, 상대습도 RH는 실제의 수증기 압력 e과 포화 수증기 압력 es의 비 (RH = 100×e/es)로 정의한다면, 포화 수증기 압력은 아래와 같은 Clausius-Clapeyron의 관계식을 통해서 결정된다[11].
| (8) |
여기서, Lv는 증발잠열, Rv는 수증기의 가스상수, 그리고 Tgas는 가스온도 [K]이다. 따라서, RH는 간단하게 아래와 같은 관계식으로 유도되고, 식 (7)과 유사한 형태를 갖는다.
| (9) |
여기서, a는 비례상수이고, b는 Lv/Rv가 된다.
특히, 가장자리들 중에 Case A에서 Right-Down, Case B에서 Left-Up 및 Right-Up, 그리고 Case C에서 Right-Center 및 Right-Down의 가스온도가 이슬점 온도 이하로 떨어지는 것으로 나타났다. 여기서, 이슬점 온도 Tdp는 관계식 (7)에 의해서 약 208.2 K로 확인되었고, Tgas < Tdp인 지점들에 대한 구분이 용이하도록 Figures 7-12에서 굵은 기호와 화살표로 표시하였다.
Figure 8은 Case A, B, 및 C에 대한 대표적인 가장자리에서 속도의 크기에 대한 대류열전달계수 h의 값들의 그래프이다. 우선적으로 그림 내에 점선으로 표시한 부분을 설명하자면, 유속의 크기가 0-0.5 m/s로 변동함에도 불구하고, 점선으로 표시된 h = 5에서 약 ±10 % 이내의 일정한 범위에서 대부분의 h 값들이 분포하였다. 특별히, Figure 7에서 RH = 100 %를 초과하는 지점들이 그 점선의 주변에 위치하였다. 이는 그 지점들에서 등온벽면과 기체 사이에 40 K의 초기 온도차 △T로 인해서 발생되는 자연대류가 우세하게 작용하였다는 것으로 쉽게 예측될 수 있다. 이를 해명하기 위해서, Figure 9과 같이 h 값들을 △T의 함수로 다시 그렸다. Case A, B, 및 C에서 등온벽면의 지점들에 대하여, 실선으로 표시된 최적 맞춤곡선의 결과로써 아래와 같은 관계식을 얻었다.
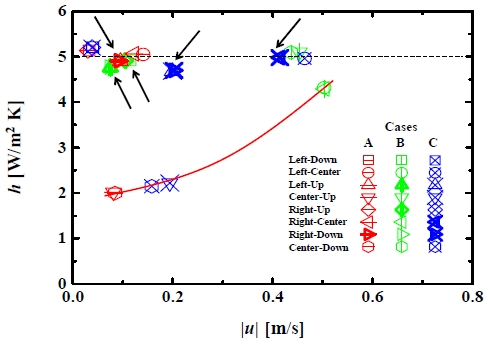
Convective heat transfer coefficients with respect to the magnitude of velocity: marked as the dotted line which indicates a dominant natural convection and the solid line which indicates a dominant forced convection
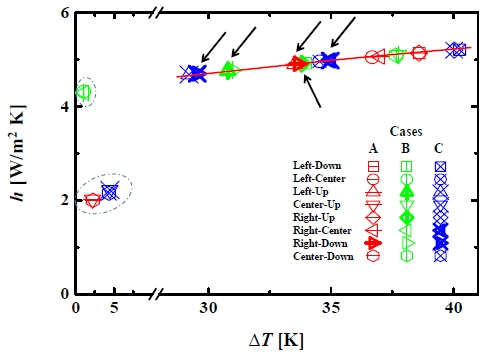
Convective heat transfer coefficients as a function of the temperature difference in the natural convection, except for the forced convection marked as the dash-dotted circles
| (10) |
이는 평판에서 자연대류에 의한 대류열전달계수의 전형적인 상관관계로써, 수평 및 수직할 때에 비례상수는 각각 1.52 및 1.31이고, 공통적인 지수는 1/3을 갖는 자연대류의 특성 [20]과 잘 일치하는 것을 확인하였다. 따라서, Figure 7에서 RH = 100 %를 초과하는 지점들은 Figure 9에서 △T 및 h의 값들의 크기가 다른 등온벽면의 지점들에서 보다 각각 상대적으로 더 낮은 범위에 있었고, 특히 LNG측 벽면의 저온부에 위치하는 것으로 파악될 수 있었다.
게다가 Figure 10에서 실선의 최적 맞춤곡선으로 나타낸 바와 같이, 자연대류에 의한 등온벽면에서 열유속은 △T에 대하여 h (≅△T0.334)의 비례상수를 갖기 때문에, 아래와 같은 상관관계를 확인하였다.
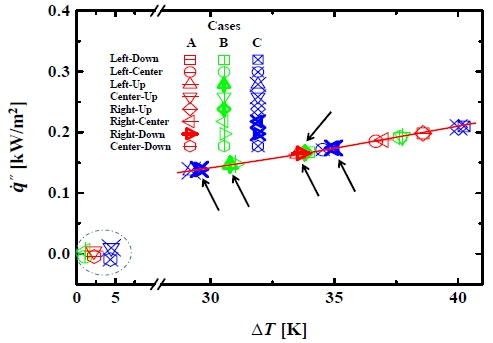
Convective heat fluxes as a function of the temperature difference in the natural convection, except for the forced convection marked as the dash-dotted circle
| (11) |
결과적으로, 식 (9-11)의 상관관계를 바탕으로, Tgas < Tdp로써 가스온도가 이슬점 이하로 하강되는 지역은 자연대류가 우세하게 나타나는 등온벽면 중에 LNG측 벽면 부근이라는 점과 상대적으로 낮은 대류열전달계수 및 열유속을 갖는다는 점이 동시에 만족되는 것으로 이해될 수 있었다.
등온 및 단열의 경계조건이 적용된 간단한 밀폐공간 내부에 대한 본 해석 결과들을 실제의 LNG 화물창의 상황으로 확대해서 유추해 본다면, 내부의 자연대류에 의한 열전달계수 h가 정지기체의 경우보다 전체적으로 상승되어 해수측 벽면에서 LNG 벽면으로 열유입량이 전반적으로 증가되기 때문에, 화물창 내에 저장된 LNG에서 증발가스의 발생량을 증가시키는 역할을 할 수 있다. 한편, 국부적인 가스온도가 상대적으로 낮아지는 지역에서 포화 수증기량을 초과할 수 있기 때문에, 영하의 가스온도에 의해서 결빙 현상이 발생될 수 있다는 것을 말한다. 그 주변은 상대적으로 작은 열유입에 의해서 지역적인 단열효과가 더 증가될 수도 있겠으나, LNG측 벽면의 온도가 국부적으로 더 낮은 온도로 유지될 수 있다. 따라서, LNG측 벽면의 선체 설계 시에 강재의 등급 및 두께 선정에 있어서, 저온의 강재 내에 온도구배에 의한 지역적인 열응력의 영향에 관한 향후 연구의 필요성을 시사하고 있다.
3.4 자연대류와 강제대류의 복합적인 열전달 특성
Case A, B, 및 C에 대한 대표적인 가장자리에서 속도의 크기에 대한 대류열전달계수 h의 값들의 그래프인 Figure 8에서, 수평의 Case A에서 Center-Down과 Center-Up, 반-수직의 Case C에서 Center-Down과 Center-Up, 그리고 수직의 Case B에서 Left-Center와 Right-Center의 순서로 h 값들이 큰 폭으로 증가되었다. 이 값들에 대한 최적 맞춤곡선의 결과로써, 아래와 같은 2차 다항식의 상관관계를 얻었고, Figure 8에서 실선으로 표시하였다.
| (12) |
이 값들은 모두 단열벽면의 중심에 위치하는 지점들로써, 유동과 단열벽면과의 온도차가 미미하기 때문에, h는 주로 증가된 유속의 크기에 의한 강제대류의 영향을 받는 것으로 확인되었다. 특히, Figure 3 (b)에서 보여준 바와 같이, 수직의 Case B에서 Left-Center 및 Right-Center의 h가 순간적으로 크게 변동되는 것은, Case A 및 Case C와는 달리, 준-정상상태에서도 단열벽면 부근에서 유속의 변화가 크다는 것을 의미하였다. 이 영역에 해당하는 지점들은 Figures 9-10에서 일점쇄선의 타원으로 표시하였고, △T에 의한 자연대류의 함수관계에 대하여 h 와 에는 무관함을 재확인하였다.
밀폐공간 내에 자연대류와 강제대류가 복합된 열전달 특성을 비교하기 위해서, 레일리 수 (Rayleigh number, Ra)의 함수로써 누셀 수 (Nusselt number, Nu)를 Figure 11에 나타내었다. 식 (10)에 근거한 자연대류가 지배적인 등온벽면에 해당하는 지점은 2×102 < Ra < 7×104의 범위에서 실선으로 표시된 바와 같이 아래의 상관관계를 보였다.
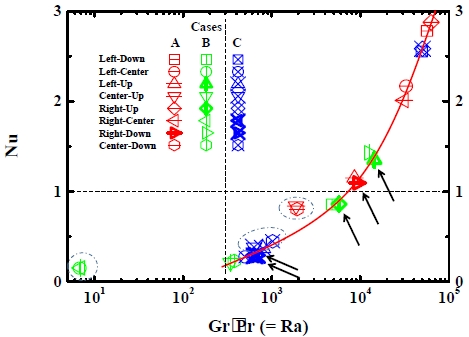
Nusselt numbers as a function of Rayleigh number (= Gr·Pr) in the natural convection, except for the forced convection marked as the dash-dotted circles
| (13) |
이러한 최적 곡선맞춤의 결과로부터 대표적인 가장자리에서 열전달은 전형적인 직사각형 밀폐공간 내에 자연대류의 특성 [20]과 잘 일치하는 것으로 확인되었다. 여기서, 대표적인 가장자리에 대한 Nu는 h·Lcell/k로, Lcell은 한 셀의 길이로 정의하였고, Ra는 Gr·Pr이고, 그라스호프 수 (Grashof number, Gr)는 gβ△T·Lcell3/ν2이고, g는 중력가속도, β는 기체팽창계수 [1/K], ν는 동점성계수이다. 그리고, 프랜틀 수 (Prandtl number, Pr)는 ν/α=μCP/k로 표현되고, μ는 점성계수, α는 열확산계수, CP는 정압비열이다. 단, Figure 11에서 일점쇄선의 타원으로 표시된 지점들은 위의 (13)의 최적 맞춤곡선에서 제외되었고, Nu가 1보다 작은 값을 갖는 영역으로 분류되었다.
또한, 복합적인 대류 열전달 특성을 비교하기 위해서, 가장자리에 대하여 Nu/Re0.5를 Gr·Re2과 동일한 리차드슨 수 (Richardson number, Ri)의 함수 [20]로써 Figure 12에 다시 나타내었다. 일반적으로, Ri < 0.1의 범위에서 Nu/Re0.5는 일정한 값을 보이다가, Ri가 그 이상으로 증가되면 단조적인 증가의 추세를 보이는 것으로 알려져 있다. 모든 가장자리에서 Pr는 약 0.5로 거의 일정하였고, Figure 11과 같이 실선으로 표시된 자연대류에 해당하는 지점들에 대해서, Figure 12에서 실선으로 표시된 바와 같이 아래의 상관관계가 도출되었다.
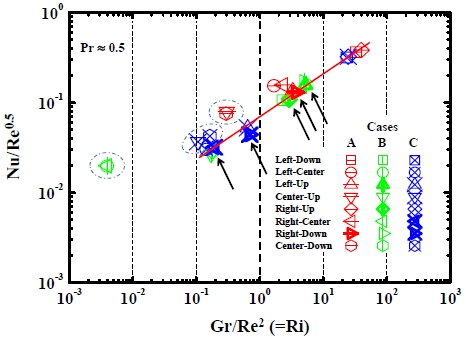
Nu/Re0.5 as a function of Richardson number (=Gr/Re2) in the natural convection, except for the forced convection marked as the dash-dotted circles
| (14) |
강제대류가 무시 가능한 수준인 Ri > 10의 범위에서, 수평의 Case A 뿐만 아니라 반-수직의 Case C에서 Left-Down과 Right-Up의 지점들은 자연대류의 열전달 특성이 우세하게 나타났다. 0.1 < Ri < 10의 범위는 강제대류와 자연대류가 복합적으로 나타난 지역으로써 RH > 100 %인 지점들도 이 영역에 분포되었다.
한편으로, Ri < 1의 범위에서 강제대류가 우세하게 작용되는 지점은 단열벽면에 대한 (12)의 관계식에 해당되는 영역으로써 위의 식 (14)의 상관관계에서 제외시켰고, Figure 12에서 일점쇄선의 타원으로 표시되었다. 특히, 자연대류가 무시 가능한 수준인 Ri < 0.01의 범위에서 수직의 Case B에서 Left-Center 및 Right-Center는 강제대류의 열전달 특성을 보였다.
4. 결 론
멤브레인형 LNG 화물창의 단열재 내부에 직사각형 밀폐공간에서 발생하는 자연대류 현상을 대와동 모사를 통하여 조사하였다. 중력 방향에 대한 등온 및 단열 벽면들의 상대적인 위치에 따라 수평의 Case A, 수직의 Case B, 그리고 반-수직의 Case C로 3 가지의 해석모델이 정의되었고, 수분이 함유된 질소기체의 열유동에 대한 국부적인 대류열전달의 특성이 비교되었다. 본 연구의 주요 결과를 아래에 요약하였다.
- ① 냉온의 등온벽면 사이에 온도차를 갖는 Case A, B, 및 C에서 초기에 정지된 기체의 대류열전달계수는 준-정상상태에 도달한 내부의 열유동에 의해서 약 2.5배 이상 증가될 수 있었다.
- ② 준-정상상태에서 평균된 물성치들의 상관관계를 분석한 결과로, 온도차에 따른 자연대류는 등온벽면 부근에서 우세하게 나타났으며, 유속의 크기에 따른 강제대류는 단열벽면 부근에서 우세하게 나타나는 것이 확인되었다.
- ③ 가스온도와 상대습도의 상관관계로부터 이슬점 온도는 약 208.2 K를 보였고, 각 Case A, B, 및 C에 대한 대표적인 가장자리들 중에 그 이슬점 온도보다 낮은 가스온도를 갖는 지점 (Tgas < Tdp)들이 나타났다.
- ④ 상대습도와 열전달 특성에 대한 분석 결과를 바탕으로, 그 Tgas < Tdp에 해당하는 영역은 자연대류에 의한 내부 열유동의 특성에 따라 LNG측 벽면 부근에 상대적으로 낮은 대류열전달계수와 열유속을 갖는 지역을 위주로 형성되는 것으로 파악되었다.
Acknowledgments
본 연구는 해양수산부의 해상부유식 LNG 벙커링 시스템 기술개발 과제에 의해서 지원되었습니다.
Author Contributions
The research presented in this paper was wholly contributed by the author.
References
- Y. S. Cho, Energy Statistics, Korea Energy Economics Institute, (2018), (in Korean).
- BP, BP Statistical Review of World Energy, 67th ed., London, UK, (2018).
-
F. Deybach, “Membrane technology for offshore LNG”, Offshore Technology Conference, OTC 15231, (2003).
[https://doi.org/10.4043/15231-ms]

- KR, KR-Rules & Guidance, (2018).
-
S. K. Yun, “Thermal analysis of LNG storage tank for LNG bunkering system”, Journal of Korean Society of Marine Engineering, 39(9), p876-880, (2015), (in Korean).
[https://doi.org/10.5916/jkosme.2015.39.9.876]

-
S. Y. Hwang, and J. H. Lee, “Comparative study on the thermal insulation of membrane LNG CCS by heat transfer analysis”, Journal of Computational Structure Engineering Institute of Korea, 29(1), p53-60, (2016), (in Korean).
[https://doi.org/10.7734/coseik.2016.29.1.53]

- H. W. Jeong, T. H. Kim, S. S. Kim, and W. J. Shim, “Thermal analysis of insulation system for KC-1 membrane LNG tank”, Journal of Ocean Engineering and Technology, 31(2), p91-102, (2017), (in Korean).
- J. H. Hu, and Y. H. Jeon, “Temperature distribution for a membrane type LNGC cargo tank”, Journal of the Society of Naval Architects of Korean, 34(4), p108-118, (1997), (in Korean).
- Energy Newspaper, July, 6), (2018, (in Korean) [Online]. Available: http://www.energy-news.co.kr/news/articlePrint.html?idxno=54453.
- Newsworks, October, 15), (2018, (in Korean) [Online]. Available: http://www.newsworks.co.kr/news/articleView.html?idxno=302779.
- K. McGrattan, S. Hostikka, R. McDermott, J. Floyd, C. Weinschenk, and K. Overholt, Fire Dynamic Simulator Technical Reference Guide Volume 1: Mathematical Model, NIST Special Publication 1018-1, 6th ed., (2017).
- T. Poinsot, and D. Veynante, Theoretical and Numerical Combustion, 3rd ed., (2012).
-
C. Kim, and B. C. Choi, “Dispersion analysis of the unignited flare gas in an LNG-FPSO vessel”, Journal of the Korean Society of Marine Engineering, 41(8), p753-759, (2017), (in Korean).
[https://doi.org/10.5916/jkosme.2017.41.8.753]

- B. C. Choi, K. H. Park, and D. H. Doh, “Impact of cold gas temperature and cylindrical obstacles on the dispersing flammable limits of accidental methane releases in an LNG bunkering terminal”, Journal of Hazardous Materials, 355, p104-110, (2018).
-
J. H. Kim, D. H. Doh, and B. C. Choi, “Evaluation of the ventilation safety requirements for the fuel gas supply system room of a gas-fueled vessel: Simulated leaks of methane and propane”, Journal of Mechanical Science and Technology, 32(11), p5521-5532, (2018).
[https://doi.org/10.1007/s12206-018-1050-7]

- K. McGrattan, S. Hostikka, R. McDermott, J. Floyd, C. Weinschenk, and K. Overholt, Fire Dynamic Simulator User’s Guide, NIST Special Publication 1019, 6th ed., (2017).
- Thunderhead Engineering, Pyrosim User Manual, (2016).
- MATLAB R2015a, The MathWorks, Inc., (2015).
- W. M. Haynes, CRC Handbook of Chemistry and Physics, 92nd ed., 6-240, (2011).
- Y. A. Çengel, Heat Transfer A Practical Approach, 2nd ed., (2005).
