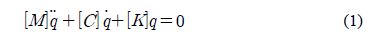Vibration characteristics of power differential gear train for 2.5MW wind turbine

1. 서 론

풍력발전기는 회전자 블레이드로부터 저속, 고 토크 형태의 동력이 입력되면 이를 기어박스가 받아서 발전기에 고속 저 토크의 동력을 전달하는 형태로 되어 있다. 특히 회전자블레이드의 정격 입력속도가 10~30rpm의 저속이지만 발전기 입력속도가 1,200~1,800rpm의 고속을 요구하기 때문에 증속비가 50~150 정도의 비교적 큰 속도비를 요구하고 있다[1]. 이와 같은 특성으로 인하여 풍력발전기 기어트레인 설계에 있어서 기술적인 차별성이 요구된다. 풍력발전기 기어트레인은 기존의 기어박스(산업용감속기, 차량변속기, 고속회전기계용 증속기 등)와는 달리, 설계에 있어서 다음과 같이 고려해야 할 특징들을 가지고 있다. ① 입지 요건에 따른 설계 가변성이 있다. ② 유지/보수 및 고공 설치 요건에 따른 경량, 소형화 설계가 필요하다. ③ ISO, AGMA 등 국제 규격에 따른 설계를 해야 한다. ④ 바람에 의해 발생되는 변동 하중에 대한 고려가 필요하다. ⑤ 돌풍 등에 따른 과도 상태 하중을 고려해야 한다. ⑥ 발전기 Short-Cut으로부터 발생된 외란 등을 설계에 반영하여야 하는 특징이 있다. ⑦ 20년 이상 수명을 보장해야 하는 특징이 있다. ⑧ 급격한 동 하중이 부과되기 때문에 동 특성 해석이 요구된다. ⑨ 높은 기어비를 구성해야 하기 때문에 기어박스 진동 소음의 문제가 특히 중요하다.

[2]에서는 굽힘, 비틀림, 축력이 연성되어 있는 헬리컬기어 쌍에 대한 일반적인 진동모델을 수립하였다. [3]에서는 헬리컬기어를 가지는 3단 공기터보압축기에 대해 로터의 질량 불평형력, 축 어긋남, 임펠러의 가진 진동수, 치합전달오차, 백래쉬 및. 베어링유격, 치접촉계수의 주기적변화로 인한 가진원 등에 대한 가진 주파수를 섭동법을 사용하여 수학적으로 정식화 하였다. [2][3]은 케이스를 포함하지 않은 헬리컬 기어 쌍에 대한 연구만 수행하였다. [4][5]는 블레이드, 기어박스, 발전기를 고려한 풍력발전시스템의 비틀림 해석을 통안 신뢰성을 검토하였다. [6]에서는 정상풍속과 돌발풍속을 수학적으로 모델링하고 풍향에 따라 전달되는 메인축에서의 전달모멘트를 조사하여 풍력발전기 기어박스에 전달되는 풍하중의 특성을 파악하였다. [7]에서는 풍력발전시스템 기어트레인의 설계요구조건을 광범위하게 고려하여, 1M∼8M 풍력발전기 기어트레인의 특성분석을 하였다. 위의 대부분의 연구는 풍력발전기 기어박스 동력전달부분만 고려하였고, 기어케이스, 유성캐리어, 토크암, 플랜지, 블레이드, 발전기의 요소를 고려한 진동특성에 대한 연구를 수행하지 않았다. 본 연구에서는 스퍼 유성기어시스템 2단, 헬리컬기어 시스템 1단으로 구성되어 있고, 메인 축과 증속기가 플랜지 결합되어 있는 동력분기식 2.5MW 풍력발전기에 대해 진동특성 분석을 하였다. 유성기어시스템, 헬리컬기어시스템, 블레이드, 메인 축, 커플링 등은 MASTA 상용프로그램으로 모델링하고, 기어박스 케이스, 토크암, 유성캐리어, 플랜지 등은 유한요소법으로 모델링하였으며, 부분구조합성법으로 조합하여 진동해석을 수행하였다. 또한 블레이드와 발전기 부분의 질량과 관성모멘트를 고려하여 블레이드와 발전기가 기어트레인의 영향을 분석하였다. 또한 2.5MW 동력분기식 풍력발전기의 고유진동 특성 해석을 수행하고, 블레이드 풍하중에 의한 가진, 질량불평형, 축 어긋남 등에 발생하는 가진원에 대해 위험속도 분석을 통하여 저감대책을 제시하였다.

2. 풍력발전기 동역학모델링

2.1 기어트레인의 방식

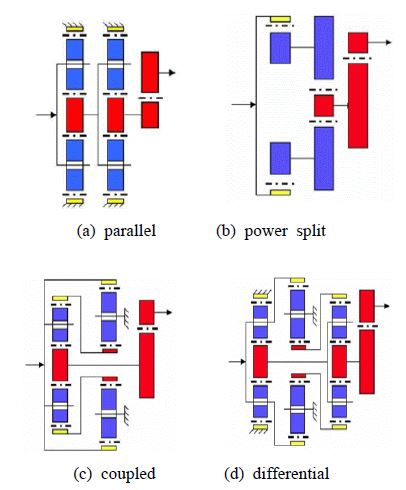
풍력발전기 기어트레인에 채택되고 있는 기어열은 Figure 1과 같이, 크게 네 가지 형태로 구분된다.

Figure 1

Gearbox concepts

Figure 1(a) 직렬형은 유성기어열과 헬리컬기어열이 직렬로 이어진 형태로서 구조가 간단하고 윤활 및 냉각에 유리하다. 특히 링기어를 고정시키는 형태로 인하여 고정 링기어가 케이스를 겸할 수 있어서 중량을 최소화하는데 유리한 입장이다. Figure 1(b) 동력 분기형은 1단에서 블기어를 입력 요소로 하고 여러 개의 피니언이 물려 있어서 1단에서 동력이 여러 경로로 분기된다. 각 경로는 독립적으로 속도를 증속시키고 출력단에 각각의 소형발전기가 장착된, 말 그대로의 동력 분기형이다. 이것은 부품 수가 늘어나는 단점이 있는 반면에 발전기의 크기를 줄일 수 있는 장점을 가지고 있어서 전체 중량은 오히려 다른 것보다 작아질 수 있는 점도 있다. Figure 1(c) 연성형은 또 다른 동력 분기형이라 할 수 있는데 마지막 출력단에서 사용되는 발전기는 하나라는 것이 동력 분기형과 다르다. 즉 회전자와 발전기 사이에 동력의 경로가 폐회로를 이루고 있는 형태이다. 이 경우는 설계가 어려워서 동력 순환이 발생할 우려도 있다. 그러나 회사마다 독특한 자신만의 모델을 확보하기 위해 여러 형태의 연성형 기어열을 개발하고 있는 실정이다. 대체로 1~3MW 정도의 중대형 발전기에서는 유성기어열 2개와 헬리컬기어단 1개로 대략 100대 1의 증속비를 내는 것으로 되어 있다. Figure 1(d) 디퍼렌셜형은 유성기어열 3개를 이용하여 다양하게 연결시켜 사용하는 형태로서, 연성시킴으로써 높은 속도비를 구현할 수 있다. 단, 구조가 복잡하고 설계가 어려운 점이 있다.

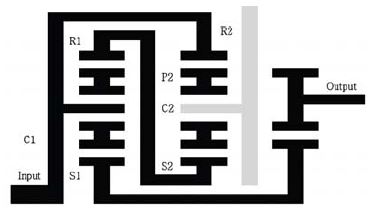
본 연구에 사용된 기어트레인은 Figure 1(c)와 같은 연성형 형태로서 스퍼유성기어열 2단과 헬리컬 기어 1단으로 이루어진 기어박스이다. 메인축(입력축)을 통하여 1단 유성기어단의 캐리어와 2단 링기어로 입력이 되며 2단 캐리어는 하우징에 고정 되어 있다. 2단 선기어는 1단의 링기어와 연결되어 있으며 1단 선기어는 3단 헬리컬 기어단의 구동기어와 결합이 되어 있다. 기어단의 레이아웃은 Figure 2와 같다. 입력으로 들어온 동력이 1단 캐리어와 2단의 링기어로 동력이 각각 약30%와 70%으로 동력이 분기가 된다. 동력 분기에 의한 효과로 기어의 사이즈를 줄일 수 있다는 장점이 있다.

Figure 2

Gear train layout

2.2 풍력발전기 진동모델링

본 연구에 사용된 풍력발전 시스템은 블레이드와 기어박스의 입력축은 플랜지 결합으로 이루어져 있으며 기어박스 출력축은 발전기와 커플링으로 결합되어 있는 구조이다. 하우징은 양쪽 토크암 마운트에 의해서 지지가 되어 있으며, 메인축은 메인 베어링에 의해서 지지되어 있다.

유성기어시스템, 헬리컬기어시스템, 축, 베어링요소와 같은 동력전달부분은 MASTA 프로그램을 통하여 모델링 하였으며, 증속기 케이스, 토크암, 유성캐리어, 플랜지 부분 등은 유한요소법으로 모델링하여 부분구조합성법을 통하여 전체 시스템을 모델링 하였다.

2.2.1 풍력발전기 파워트레인 부분 모델링

본 연구에 사용된 기어 제원은 다음과 같다. 총 증속비는 1:72이다. 1단, 2단 유성기어시스템, 3단 헬리컬기어시스템, 메인 축 등은 MASTA 상용프로그램으로 모델링하였다. 해석에 사용된 기어제원은 Table 1과 같다.

유성기어시스템, 헬리컬기어시스템은 여러 개의 축으로 이루어져 있다. 각기 따로 움직이는 축들은 기어를 통해서 연성이 된다. Table 1에 따라 생성된 기어의 질량 및 강성 행렬은 축의 강성, 질량, 자이로스코프 행렬과 결합이 되며, 축은 베어링의 강성행렬과 결합이 되어 기어트레인의 시스템행렬이 생성된다.

Table 1

Gear information

2.2.2 케이스 모델링

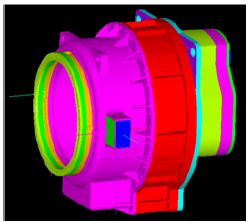
케이스는 유한요소법으로 모델링을 하고 MASTA 프로그램과 연성시켜 진동해석을 수행한다. 케이스의 유한요소 모델링은 기어트레인의 베어링와 연결한다. 하지만 이 거대한 유한요소의 모델을 그대로 사용하면 시작적인 측면에서 효율적이지 못하다. 따라서 부분구조합성법을 통하여 케이스의 질량, 강성행렬사이즈를 축소하여 기어트레인과 연결시킨다[8]-[10]. Figure 3은 본 연구에 사용된 케이스의 형상을 나타낸다.

풍력발전기용 증속기는 일반적으로 케이스 양쪽의 토크암 마운트를 통하여 지지되어 있는 형태을 취한다. 본 연구에서는 ANSYS프로그램을 사용하였으며, 빔 요소를 통하여 토크암 양쪽에 지지강성을 부여 하였다. 토크암 마운트는 combination spring-damper14요소를 사용하여 구현하였다. 양쪽 각각의 토크암에는 4개의 spring요소를 사용하여 운동을 구속 시켰다. Table 2는 토크암 강성값을 나타낸 것이다.

Figure 3

Housing reduction analysis

Table 2

Torque arm stiffness information

2.2.3 특이형상 모델링

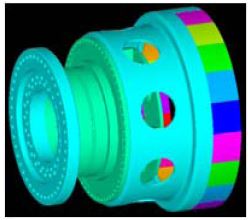
캐리어는 유성기어를 지지하는 핀과 연결되어 있기 때문에 유성기어단의 진동특성에 직접적인 영향을 미친다. 캐리어와 플랜지 역시 케이스와 마찬가지로 그형상이 복잡하여 단순한 축 모델로는 그 특성을 제대로 부여하기가 어렵다. 따라서 캐리어 및 플랜지를 유한요소법으로 모델링하고, 부분구조합성법을 통하여 그 특성을 부여하였다.

Figure 4, 5는 캐리어와 축 요소를 나타내고 있다.

Figure 4

Carrier Shaft - 1 step reduction analysis

Figure 5

Coupling Shaft - 2 step reduction analysis

2.2.4 블레이드, 발전기 모델링

풍력발전시스템은 타워와 너셀을 제외하고 크게 블레이드, 기어박스, 발전기로 그 덩어리를 나눌 수 있다. 블레이드는 그 무게와 모멘트의 크기 자체가 다른 그 무엇보다 크기 때문에 고유진동특성에 미치는 영향은 크다. 블레이드는 관성 모멘트와 질량을 가지는 디스크 요소로 모델링 하였다.

발전기는 고정자와 회전자로 구성되어 있다. 회전자가 회전을 하면서 전기를 발생하는 구조로서 기어박스의 출력축은 발전기의 회전자와 결합이 되어 있다. 발전기는 회전자의 회전관성모멘트를 고려하고 기어박스의 출력축과 회전자는 커플링을 통하여 결합하였다.

해석에 사용한 블레이드, 커플링은 Table 3과 같다.

Table 3

Blade, coupling information

2.2.5 2.5MW 풍력발전기 기어트레인 고유특성 해석

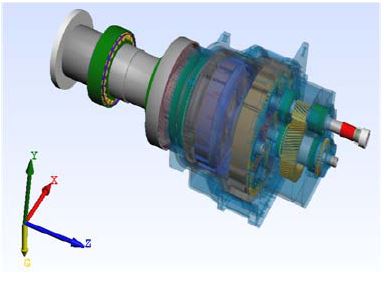
유성기어시스템 2단, 헬리컬기어시스템 1단, 축, 베어링요소와 고속축 커플링, 블레이드 등 은 MASTA 프로그램을 통하여 모델링 하였으며, 증속기 케이스, 토크암, 유성캐리어, 플랜지 부분 등은 유한요소법으로 모델링하여 부분구조합성법을 통하여 전체 시스템을 모델링 하였다. 시스템의 전체적인 형상은 Figure 6과 같다.

Figure 6

2.5MW wind turbine gear train

2.5MW 풍력발전기 기어트레인 진동시스템은 식 (1)과 같이 나타 낼 수 있다.

여기서 [M]은 시스템 질량 행렬, [C]는 시스템 감쇠행렬, [K]은 시스템 강성 행렬이다. q는 시스템의 자유도이다. Table 4는 블레이드, 발전기의 질량과 관성모멘트를 포함 할 경우와 기어박스만을 고려한 2.5MW 풍력발전기 시스템에 대해 고유진동수를 구한 결과를 나타낸 것이다.

1차 고유진동수 1.95Hz는 기어박스만 고려한 모델에는 나타나지 않음을 알 수 있다. 풍력발전기 기어트레인을 모델링 할 때, 블레이드의 질량효과를 고려해야 함을 알 수 있다. 1차는 블레이드의 회전운동으로 기어박스 및 토크암에 변형이 크게 발생하는 모드이며, 2차는 1단 링기어와 2단 선기어의 축방향운동이 주도하는 모드이다. 3차, 4차, 5차 모드는 하우징 덩어리의 운동에너지가 높으며 이를 지지하는 토크암 마운트, 입력축, 메인베어링에 변형이 크게 발생하는 모드이다. 6차, 8차는 블레이드의 병진운동으로 인하여 기어박스 및 토크암에 변형이 발생하는 모드이다. 1차, 6차, 8차는 블레이드의 질량 및 관성모멘트가 주도하여 발생하는 모드로서 블레이드를 모델링에 포함하지 않았을 때에는 그 특성이 보이지 않는다. 이는 풍력발전시스템을 해석할 때, 블레이드의 질량 및 관성효과를 포함해야 한다는 것을 의미한다.

Table 4

Natural frequency

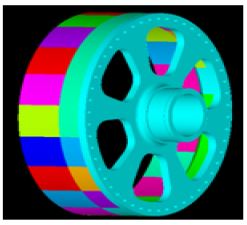
Figure 7은 2차 고유모드의 탄성에너지 저장율을 나타낸 그림이다. 1단 링기어 & 2단 선기어축 조합의 축방향 운동이 나타나는 모드로서 이를 지지하고 있는 베어링에 변형이 크게 생긴다. 이 모드는 1단 링기어 & 2단 선기어축의 질량과 이를 지지하는 베어링의 강성 값이 고유진동수 및 고유모드를 결정짓는 주요 인자이다. 이 모드에서는 축 조합을 지지하고 있는 베어링의 축 방향 강성을 증가 및 감소시키면 고유진동수를 상향 및 하향 조절할 수 있다.

Figure 7

2nd mode shape

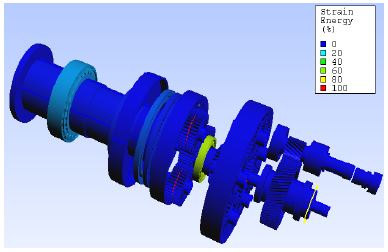
Figure 8은 3차 고유모드를 나타낸 그림이다. 거대한 기어박스 덩어리가 운동을 주도하는 모드이며, 이를 지지하고 있는 토크암 마운트, 메인축 및 메인축 지지베어링에 탄성에너지 저장율이 높은 모드이다. 메인축의 직경 또는 메인축 지지베어링의 위치변경 그리고 토크암 마운트의 강성의 변화로 고유진동수 변화를 줄 수 있다. 4차와 5차는 3차와 유사한 형태를 보인다.

Figure 8

3rd mode shape

Figure 9는 6차 고유모드형태이다. 1단 선기어와 3단 헬리컬 구동기어를 연결하는 연결축에 탄성에너지 저장율이 높은 모드이다. 축 직경의 증가를 통하여 고유진동수를 상향 조절하면 공진의 발생지점이 보다 구동범위의 경계 쪽으로 이동을 시킬 수 있을 것이다.

Figure 9

6th mode shape

3. 2.5MW 풍력발전기 기어트레인 위험속도 분석

3.1 기어트레인 가진 진동원

회전체 시스템에 있어서 시스템에 내포하고 있는 자려 가진과 외력 가진을 파악하여 공진 여부를 파악하고 이를 회피하는 것이 중요하다[3].

풍력발전시스템에 작용하는 가진은 크게 블레이드, 파워트레인, 발전기 부분으로 나눌 수 있다. 블레이드에서는 블레이드 개수에 비례하는 가진 주파수를 가지고 있다. 본 연구 대상의 블레이드의 날의 개수가 3개이므로 블레이드의 풍하중에 의해서 발생하는 가진은 3X이다. 여기서 X는 입력축의 회전속도이다. 파워 트레인부분에서는 질량 불평형, 베어링 결함, 축정렬오차 등에 의한 가진요소 등이 있다. 질량 불평형은 축의 회전속도에 비례하게 발생을 하며, 축과 축 사이를 연결하는 커플링요소에서 발생하는 가진은 축의 회전속도에 2배에 비례하며 발생한다.

본 연구에서는 블레이드에서 발생하는 가진과 질량 불평형 및 커플링 요소에서 발생하는 축정렬 오차를 고려하여 가진원을 정리하였다. 가진 주파수비는 Table 5와 같다.

Table 5

Excitation frequency ratio

3.2 위험속도 분석

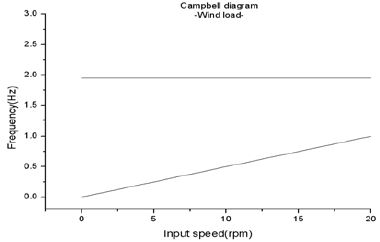
본 연구의 풍력발전기의 정격 운전속도는 15rpm이며, 구동되는 작동범위를 0~20rpm으로 설정하여 위험속도 해석을 수행하였다. Figure 10, Figure 11, Figure 12는 블레이드에서 발생하는 가진, 질량 불평형에 의한 가진, 축정렬 오차에 가진에 대해 위험속도 분석을 한 그래프를 나타낸다.

Figure 10은 풍하중에 의해서 블레이드에서 발생하는 가진 주파수에 대한 위험속도 해석을 한 것이다. 그래프 결과 구동범위 내에서는 공진이 발생하지 않는 것을 확인 하였다. 이 가진에 의해서 공진이 발생한다면 소음보다는 저주파의 진동이 발생할 수 있다. 진동은 시스템의 내구성에 직접적인 영향을 주므로 저차 모드에서 발생하는 공진 확인 풍력발전시스템에서 중요하게 확인하여야 할 모드이다.

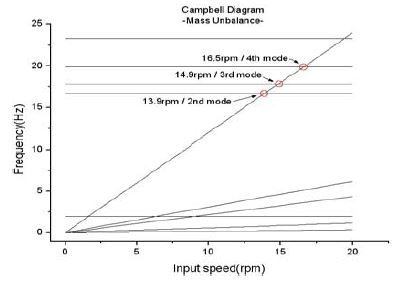
Figure 11은 질량 불평형에서 발생하는 가진 주파수에 대한 위험속도 해석을 한 것이다. 3단 출력축의 질량 불평형에 의해서 정격구동속도 영역인 13~17rpm 영역에서 공진이 발생하고 있다. 질량 불평형에 의해서 발생하고 있는 공진은 2~4차 고유진동수에 의해서 발생을 한다. 이 위험속도에 대해 진동을 저감하기 위해서는 기어요소의 밸런싱 또는 축의 직경을 증가시켜 고유진동수를 상향 조절하여 위험속도를 제거하여야한다.

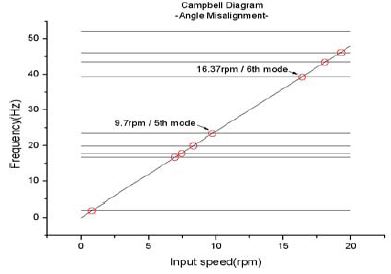
Figure 12은 출력축 고속축 커플링에 의한 축정렬 오차 가진에 의한 위험속도 해석을 확인한 그래프이다. 운전속도 15rpm 근처에 16.37rpm의 위험속도가 존재하고 고유모드는 6차모드 39.67Hz를 나타낸다. 6차모드는 Figure 9에 나타내었다. 축 직경의 증가를 통하여 고유진동수를 상향 조절하거나 고속축 커플링에 연결되어 있는 축에 대한 정밀한 축정렬이 요구됨을 알 수 있다.

Figure 10

Campbell diagram - blade excitation

Figure 11

Campbell diagram - mass unbalance

Figure 12

Campbell diagram - axial misalingnment

4. 결 론

스퍼 유성기어시스템 2단, 헬리컬기어 시스템 1단으로 구성되어 있고, 메인 축과 증속기가 플랜지 결합되어 있는 동력분기식 2.5MW 풍력발전기에 대해 진동해석을 수행하였다.

1. 유성기어시스템, 헬리컬기어시스템, 블레이드, 메인 축, 커플링 등은 MASTA 상용프로그램으로 모델링하고, 기어박스 케이스, 토크암, 유성캐리어, 플랜지 등은 유한요소법으로 모델링하였으며, 부분구조합성법으로 조합하여 진동해석을 수행하였다.

2. 풍력발전기 기어박스에 블레이드 질량효과를 고려한 모델과 기어박스만 고려한 모델의 고유진동수를 비교하였다. 1차 고유진동수 1.95Hz는 기어박스만 고려한 모델에는 나타나지 않았으며, 풍력발전기 기어트레인을 모델링 할 때, 블레이드의 질량효과를 고려해야 함을 알 수 있었다.

3. 풍하중에 의해서 블레이드에서 발생하는 가진, 질량 불평형에 의한 가진, 고속축 커플링 요소에서 발생하는 축정렬 오차를 고려한 가진원에 대해 위험속도 분석을 하였다.

1) 블레이드에서 발생하는 가진원에 대한 위험속도 분석결과 공진이 발생하지 않음을 알 수 있었다.

2) 질량 불평형에서 발생하는 가진 주파수에 대한 위험속도 해석을 한 결과, 3단 출력축의 질량불평형에 의해서 정격구동속도 영역인 13~17rpm 영역에서 공진이 발생하였다. 이 위험속도에 대한 진동을 저감하기 위해서는 기어요소의 밸런싱 또는 축의 직경을 증가시켜 고유진동수를 상향 조절하여야 함을 알 수 있었다.

3) 축 정렬 오차 가진에 의한 위험속도 해석을 한 결과. 운전속도 15rpm 근처에 16.37rpm의 위험속도가 존재하였다. 축 직경의 증가를 통하여 고유진동수를 상향 조절하거나 고속축 커플링에 연결되어 있는 축에 대한 정밀한 축정렬이 요구됨을 알 수 있었다.

4. 향후에, 풍력발전기 기어트레인의 이론분석에 대한 실험검증 및 신뢰성평가에 대한 연구가 필요할 것으로 사료된다.

Acknowledgments

* 본 연구는 ''산업통상자원부'', ''한국산업기술진흥원'', ''동남지역사업평가원''의 ''광역경제권 선도산업 육성사업''으로 수행된 연구결과입니다.

References

• S. Heier, and R. Waddington, Grid Integration of Wind energy conversion system, 2nd Edition, John Wiley & Son, Ltd, p111-116, (2006).
• H. W. Lee, D. H. Jung, and N. G. Park, “A study on dynamic characteristics of gear-system”, Journal of the Korean Society for Noise and Vibration Engineering, 10(1), p74-81, (2000), (in Korean).
• H. W. Lee, D. H. Lee, and N. G. Park, “An analytical investigation on vibrational characteristics of turbo compressor”, Journal of the Korean Society for Noise and Vibration Engineering, 8(6), p1069-1077, (1998), (in Korean).
• Jung Su Kim, Hyoung Woo Lee, No Gill Park, Young Duk Kim, Soo Yum Kim, and Dong Hwan Lee, “Characteristic of vibration in wind turbine system”, Journal of the Korean Society of Marine Engineering, 35(6), p786-795, (2011), (in Korean).
• Michael Todorv and Georgi Vukov, “Modal properties of drive train in horizontal-axis wind turbine”, Proceedings of International Conference on Innovations, Recent Trends and Challenges in Mechatronics, 3, p160-168, (2011).
• J. S. Kim, H. W. Lee, N. G. Park, and Lee. D. H, “A study on wind load variation characteristics of wind turbine gearbox”, Journal of the Korean Society of Marine Engineering, 36(2), p267-275, (2012), (in Korean). [https://doi.org/10.5916/jkosme.2012.36.2.267]
• N. G. Park, and H. W. Lee, “An investigation on the characteristics of gear trains of wind turbines”, Journal of the Korean Society of Marine Engineering, 34(6), p806-815, (2010), (in Korean). [https://doi.org/10.5916/jkosme.2010.34.6.806]
• W. C. Hurty, “Vibrations of structural systems by component mode synthesis”, Journal of the Engineering Mechanics Division, 86, p59-69, (1960).
• W. C. Hurty, “Dynamic analysis of structural systems using components modes”, American Institute of Aeronautics and Astronautics, 3(4), p678-685, (1965). [https://doi.org/10.2514/3.2947]
• R. R. Craig, and M. C. C. Bampton, “Coupling of substructures for dynamic analysis”, American Institute of Aeronautics and Astronautics, 6, p1313-1319, (1968).