CFD를 이용한 림 구동 일체형 추진장치의 단독성능 예측
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 Ka4-70 프로펠러 날개와 No. 19A 덕트 형상을 기반으로 설계된 림 구동 일체형 추진장치의 단독성능을 예측하기 위한 전산유체역학(CFD) 해석 결과를 제시하였다. 상용 CFD Solver인 Fluent를 활용하여 추진장치가 선체에 장착되지 않은 상태에서 캐비테이션을 고려하지 않은 조건과 고려한 조건에 대한 해석을 수행하였다. 추진기의 회전은 MRF(Moving Reference Frame) 기법을 통해 표현하였고, 캐비테이션에 의한 이상유동과 액체-증기 간의 물질전달을 모사하기 위해 Mixture Model 및 Schnerr-Sauer Model을 적용하였다. 해석 결과, 림 구동 추진장치는 기존의 축 구동 추진장치에 비해 효율이 다소 낮아지고 다른 캐비테이션 특성이 나타나며, 프로펠러 허브 유무에 의해 유체역학적 특성이 변화함을 확인할 수 있었다. 또한 전동기 고정자 장착을 위해 설계 변경된 덕트 형상과 롤 제어를 위해 설치된 스월 스테이터가 추진성능에 미치는 영향에 대해서도 분석을 수행하였다.
Abstract
This study presents numerical results for the open-water performance of a rim-driven integrated propulsor designed based on the Ka4-70 propeller blade and No. 19A duct geometry. Computational fluid dynamics (CFD) simulations of non-cavitating and cavitating flows were conducted with the propulsor not mounted to the hull using commercial Reynolds-averaged Navier–Stokes solver (Fluent software). The rotation of the propeller was described by the moving reference frame method. Mixture and Schnerr–Sauer models were used to simulate two-phase flow and mass transfer by cavitation. The simulation results showed that the developed rim-driven propulsor had lower open-water efficiency and exhibited different cavitational characteristics compared with the conventional shaft-driven propulsor, and the hydrodynamic characteristics changed according to the presence or absence of a propeller hub. In addition, we investigated the effects of modified duct shapes and additional swirl stators for roll control on the performance.
Keywords:
Rim-driven integrated propulsor, Open-water performance, Computational fluid dynamics (CFD), Moving reference frame (MRF), Cavitation, Propeller hub키워드:
림 구동 일체형 추진장치, 단독성능, 전산유체역학, MRF (Moving Reference Frame), 캐비테이션, 프로펠러 허브1. 서 론
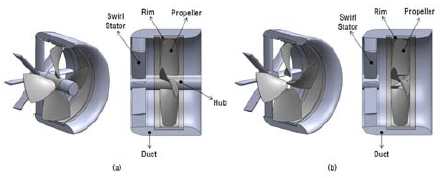
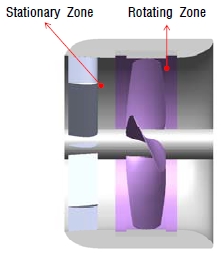
잠수함, 어뢰, 무인잠수정 등의 수중운동체와 선박은 기본적으로 수중 추진장치를 회전시켜 발생하는 추력에 의해 전진한다. 수중 추진장치는 스크류 형태의 프로펠러, 프로펠러를 회전시킬 수 있는 동력원인 전동기(Motor), 그리고 전동기와 프로펠러를 연결시켜 주는 축계로 구성되어 있다. 최근 들어 프로펠러와 전동기, 축계를 일체화시킨 일체형 추진장치가 개발되어 사용되고 있다. 특히 림 구동 일체형 추진장치는 프로펠러 덕트 내부에 위치한 전동기 고정자(Stator)와 프로펠러 끝단(Tip)의 림(Rim)에 위치한 회전자(Rotor)의 반발력에 의해 회전하는 구조로서(Figure 1), 기존의 전동기가 회전하면 전동기에 연결된 축과 축에 연결된 프로펠러가 회전하는 축 구동(Shaft-driven) 방식의 추진장치와 비교했을 때 많은 장점을 지니고 있다. 우선 전동기가 추진기 덕트 내부에 위치하므로 전동기 장착 공간의 효율적 활용이 가능하다. 전동기와 프로펠러를 연결하는 축계가 없어도 되기 때문에 장기 운용 시 수밀 구조의 신뢰성 문제 해결과 방사 소음 저감이 가능하며, 프로펠러의 방향 전환에 의해 선체의 자세 및 방향 제어를 할 수 있는 벡터 스러스트(Vectored Thrust) 구현이 용이하다. 이와 같은 장점들로 인해 수중에 장기간 체류하는 무인잠수정과 잠수함의 주 추진장치로 림 구동 일체형 추진장치를 적용하기 위한 연구가 활발하게 진행되고 있으며(K. B. Kim et al. [1]), 선박의 저속 주행 시 미세제어를 위한 측면 추력장치(Bow Thruster)로 활용하기에도 적합하므로 이와 관련된 연구 역시 활발하게 진행되고 있다.
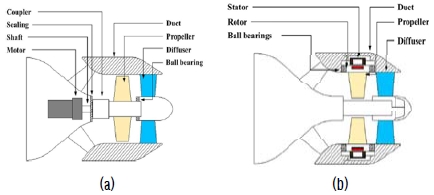
Mechanical Structures of marine propulsors (examples) (a) conventional shaft-driven propulsor (b) rim-driven propulsor
림 구동 일체형 추진장치의 프로펠러는 끝단에 림이 장착되어 있기 때문에 기존의 덕트 프로펠러와 비교해서 유체역학적 특성이 변화하게 되며, 그에 따라 추력/토크/효율 등의 추진성능과 캐비테이션 특성도 달라질 것으로 예측할 수 있다. 전통적으로 프로펠러의 유체역학적 특성을 도출하기 위해 예인수조 혹은 대형 캐비테이션 터널(Large Cavitation Tunne, LCT)에서 수행하는 모형시험이나 포텐셜 유동 기반의 보텍스 격자법(Vortex Lattice Method, VLM), 패널법(Panel Method) 등이 많이 활용되어 왔다. 최근 들어서는 프로펠러 주위의 점성 유동을 직접 모사하는 CFD(Computational Fluid Dynamics)의 활용 빈도가 점점 증가하고 있다. H. R. Yu et al. [2]은 전치 가이드 베인을 갖는 수중 덕트 프로펠러에서 가이드 베인과 프로펠러의 상호작용을 포함한 유동해석을 수행하였으며, T. H. Joung et al. [3]은 상용 CFD 소프트웨어를 이용한 유동해석을 수행하여 덕트 형상에 따른 덕트 프로펠러의 단독성능 곡선을 도출하고 모형시험 결과와 비교하였다. S. B. Suh [4]는 덕트와 핀을 활용한 복합형 추진효율 향상 장치의 성능에 대한 CFD 해석 결과를 제시하였으며, J. I. Kim et al. [5]은 SVA Potsdam 프로펠러의 단독 및 캐비테이션 성능을 예측하기 위한 CFD 해석을 수행하였다. 이처럼 많은 연구자들이 추진장치의 성능 분석을 위해 CFD를 활용하고 있으며, 컴퓨터 성능 및 수치해석 기법의 급격한 발전에 힘입어 계산 속도와 결과의 정확도 또한 비약적으로 향상되고 있는 추세이다.
본 연구에서는 림 구동 일체형 추진장치에 대하여 선체에 장착되지 않은 상태의 단독성능을 예측하기 위한 CFD 해석을 수행하였으며, 추가적으로 림 구동 추진장치의 허브(Hub) 유무에 따른 특성 변화에 대해서도 확인하였다. 캐비테이션을 고려하지 않은 조건과 고려한 조건에서의 무차원화된 추력/토크/효율 곡선을 도출하였고 프로펠러 날개 주위의 캐비테이션 발생 양상에 대해서 모사하였다. 이를 통하여 기존 축 구동 프로펠러 대비 림 구동 프로펠러의 유체역학적인 성능 변화를 사전에 예측함으로써, 실제 수중운동체 주 추진장치로의 적용 가능성을 사전에 검증해 보고자 하였다. 본 연구에서의 CFD 해석은 유한체적법(Finite Volume Method, FVM) 기반의 상용 소프트웨어인 ANSYS Fluent를 이용하여 수행되었다(ANSYS Inc. [6]).
2. 추진장치 형상설계
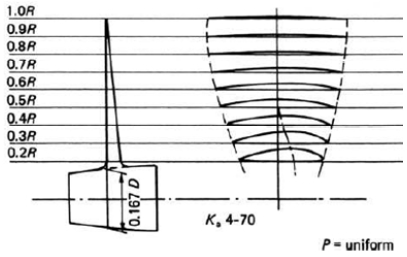
본 연구에서는 직경 21인치 크기의 원통형 무인잠수정에 적용하기 위한 림 구동 일체형 추진장치를 설계하였다. 무인잠수정은 장시간 동안 수중에서 다양한 임무를 수행해야 하기 때문에, 그 추진장치는 장기 운용 신뢰성, 주행속도, 롤(Roll) 안정성, 저소음 특성이 충족되도록 설계되어야 한다. 림 구동 추진장치는 프로펠러 날개, 덕트, 프로펠러 날개 끝단의 림 내부에 위치한 전동기 회전자, 덕트 내부의 전동기 고정자, 스월 스테이터(Swirl Stator), 베어링 등으로 구성된다. 프로펠러 날개는 추진장치 추력과 소음의 대부분을 발생시키며 추진장치 최적화 설계에 있어 가장 핵심적인 구성품이다. 프로펠러 날개의 단면 형상은 덕트 프로펠러 중에서 가장 잘 알려져 있고 많이 사용되는 Ka-Series(Carlton [7]), 그 중에서도 4개의 날개를 가지며 확장면적비(Expanded Area Ratio, AE/AO)가 0.7인 Ka4-70을 적용하였다(Figure 2). 저소음화 및 캐비테이션 발생 최소화를 위해서는 추진장치가 높은 전진비(=낮은 회전수)에서 큰 추력을 낼 수 있어야 하므로, 피치 대 직경비(Pitch to Diameter Ratio, P/D)를 1.4로 다소 크게 설정하였다. 프로펠러 끝단에는 전동기 회전자가 들어갈 수 있도록 림이 부착되는데, 유체역학적으로는 저항의 역할을 하므로 크기를 최소화하는 것이 바람직하다.
General outline of Ka4-70 Propeller
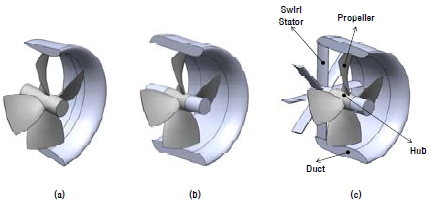
덕트는 전동기 고정자가 설치될 수 있는 크기여야 하고, 아울러 프로펠러에 유입되는 유동을 가속시켜 효율을 증가시키고 유동저항을 최소화시킬 수 있어야 한다. 본 연구에서는 Ka-Series와 함께 자주 사용되는 No.19A 형상(Carlton [7])을 기반으로 덕트 형상을 설계하였다(Figure 3). 단, No. 19A를 그대로 적용할 경우 덕트 내부에 전동기 고정자를 설치할 수 없으므로, 덕트 내경의 유동 입구와 출구는 No. 19A의 프로파일을 그대로 적용하되 평행부의 길이를 증가시키고 외경의 프로파일은 변경하는 방향으로 덕트 형상을 수정하였다. 덕트 내경 중 프로펠러 날개의 림이 있는 부분은 안쪽으로 홈이 파여 있으며, 이는 림에 의한 유동저항 증가를 최소화하고 프로펠러 날개 직경을 확보하기 위한 것이다. Figure 3은 원래의 No. 19A 덕트(a)와 수정된 형상의 축 구동 추진장치용(b), 림 구동 추진장치용(c) 덕트 형상을 나타내고 있다.
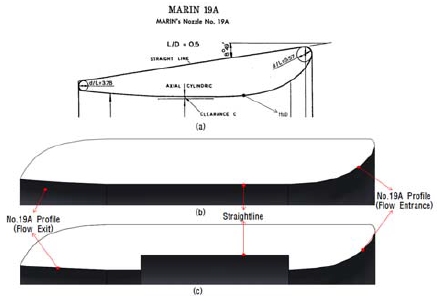
Duct outline of (a) Original No. 19A (b) conventional shaft-driven propulsor (c) rim-driven propulsor
원통형 무인잠수정은 롤 거동에 대한 감쇠력이 작기 때문에, 주행 안정성 및 조종성능 확보를 위해서는 운전 조건에서의 롤 불균형을 최소화할 필요가 있다. 스월 스테이터는 프로펠러 날개에서 발생하는 것과 반대 방향의 롤 모멘트를 발생시키며, 아울러 덕트를 구조적으로 지지하는 역할도 하게 된다. 비대칭 NACA 단면을 적용하여 롤 모멘트 크기를 극대화함과 동시에, 후류의 회전 운동에너지를 회수하고 스월 스테이터에 의해 추력이 발생하는 방향으로 각도 설정이 가능하게 함으로써 추진장치의 효율을 향상시킬 수 있도록 설계하였다(Figure 4). Table 1은 설계된 프로펠러의 최종 제원을 나타낸 것이다.
Configuration of rim-driven propulsor (a) with hub (b) without hub
Geometric parameters of propeller and duct
림 구동 일체형 추진장치는 축에 의해 동력을 전달받는 방식이 아니기 때문에, 베어링 지지구조에 따라 프로펠러 중심부에 있는 허브를 제거할 수도 있다. 본 연구에서는 허브(Hub) 유무에 따른 2가지 종류의 프로펠러에 대해 유동 해석을 수행하여 허브 제거 시 프로펠러의 유체역학적 특성이 어떻게 변화하는지 확인하고자 하였다. 이 때 프로펠러 날개의 형상과 제원은 동일하게 설정하였다.(Figure 4)
기존 형태의 축 구동 추진장치의 경우에는, 해석 모델 타당성 검증을 위해 Figure 5 (a)와 같이 설계 변경되지 않은 No. 19A 덕트 적용, Figure 5 (b)와 같이 홈이 없는 것을 제외하고 림 구동 추진장치와 동일하게 수정된 형상의 덕트 적용, Figure 5 (c)와 같이 스월 스테이터가 추가 장착, 이상의 3가지 종류에 대한 유동해석을 수행하였다. 프로펠러 날개 형상 및 크기는 림 구동 추진장치와 동일하게 설정하였으며, 축 구동 추진장치의 프로펠러 날개 외경은 림 구동 추진장치의 림 내경과 같다. 프로펠러 날개 외경과 덕트 내경 사이의 간격(Gap)은 1mm이다.
Configuration of conventional shaft-driven propulsor (a) original Ka4-70 with unmodified No. 19A duct (b) with modified duct and without swirl stator (c) with modified duct and with swirl stator
3. 수치 해석
3.1 지배방정식 및 해석 기법
CFD에 의한 유동해석을 수행할 때 풀게 되는 유체의 지배방정식은 연속방정식(Continuity Equation)과 흔히 Navier-Stokes Equation이라고 부르는 운동량 방정식(Momentum Equation)이며, 전체 유동을 완전히 발달된 난류로 가정할 때 다음과 같은 식으로 나타낼 수 있다.
| (1) |
| (2) |
식 (2) 우변의 맨 오른쪽 항은 난류 유동의 변동 성분에 대한 항이며, Boussinesq 모델을 통하여 다음과 같이 나타낼 수 있다.
| (3) |
결국 Bousinesq 모델에 기반한 난류 모델에서는 난류 점성(Turbulent Viscosity, μt)을 구하는 것이 목적이 된다. 다양한 종류의 난류 모델 중, 본 연구에서는 k-ω모델과 k-ε모델의 장점을 결합한 SST(Shear Stress Transport) k-ω난류 모델을 적용하였다. SST k-ω모델은 벽면 근처의 Inner Layer에서는 수정된 Standard k-ω모델을 적용하고 그 외의 영역에서는 k-ε모델로부터 변환된 k-ω모델을 적용하는 방식으로서, 외부 유동 및 회전체 유동 해석에 있어서 가장 안정적이고 정확한 결과를 보여주는 것으로 알려져 있다(J. I. Kim et al. [5]).
본 연구에서는 추진장치 주위 유동을 밀도가 일정한 비압축성 유동(Incompressible Flow)으로 가정하였으며, 압력-속도 연성(Pressure-Velocity Coupling) 방법으로는 단상 유동 및 다상 유동에서 모두 안정적인 Pressure-Based Coupled Method를 적용하였다.
3.2 캐비테이션 모델
캐비테이션은 고속으로 움직이는 물체 주위의 압력강하로 주위 액체가 증기 상태로 기화하는 현상이다. 프로펠러 날개가 고속으로 회전하게 되면 물체 표면에서는 압력이 낮아지며, 이 압력이 증기압(Vapor Pressure, pv)보다 낮아지면 캐비테이션이 발생한다. 캐비테이션이 발생하면 추력 손실로 인한 효율 감소, 캐비테이션이 붕괴할 때 생기는 충격파에 의한 소음 발생 및 날개면 침식, 선체 변동압력 증가 등 나쁜 영향을 미치기 때문에, 캐비테이션 특성을 예측하는 것은 프로펠러 설계에 있어서 매우 중요한 일이다.
캐비테이션이 발생하면 액체와 증기 2가지 상(Phase)이 존재하게 되므로, 다상유동(Multi-phase Flow) 해석을 수행하여야 한다. 본 연구에서는 Mixture Model을 적용하여 액체와 증기 2가지 상이 존재하는 캐비테이션 유동에 대한 CFD 해석을 수행하였다. Mixture Model은 각 상에 대해서 지배방정식을 따로 푸는 것이 아니라 유체가 각 상의 혼합물인 것처럼 간주하여 1개의 상이 있을 때와 같은 수의 지배방정식을 푸는 방식이다. 밀도와 점성 등 유체의 물성치는 각 상의 체적분율(Volume Fraction)에 따라 다음과 같이 정의한다.
| (4) |
| (5) |
여기서 아래첨자 l은 액체상(Liquid Phase), v는 증기상(Vapor Phase)을 나타내며 α는 유체의 체적분율을 나타낸다.
캐비테이션 유동 해석을 위해서는 캐비테이션의 생성과 소멸 메커니즘을 포함하는 증기의 체적분율에 대한 보존방정식이 추가적으로 필요하며, 다음과 같이 나타낼 수 있다.
| (6) |
여기서 uv는 증기의 속도를 나타내며 Re는 캐비테이션 생성에 의해 액체에서 증기로 변화하는(Evaporation) 물질전달률, Rc는 캐비테이션 소멸에 의해 증기에서 액체로 변화하는(Condensation) 물질전달률을 의미한다. Re와 Rc는 Schnerr-Sauer Model(Schnerr and Sauer [8])에 의해 다음과 같이 표현할 수 있다.
| (7) |
when P ≤ Pv
| (8) |
when P ≥ Pv
RB는 증기 기포의 반경이며 아래의 식으로 표현된다.
| (9) |
n은 유체 단위체적 당 증기 기포의 개수이며, 본 연구에서는 ANSYS Fluent에서 권장하는 값인 1×1011/m3을 사용하였다(ANSYS Inc. [6]).
3.3 해석 모델 및 경계조건
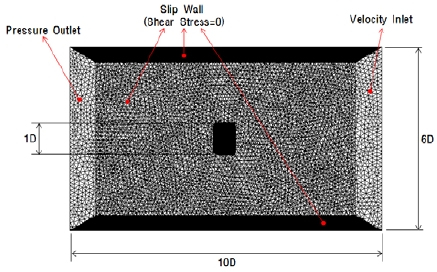
Figure 6은 본 연구에서 수행한 해석 모델 및 경계 조건을 나타낸 것이다. 위벽효과(Blockage Effect) 등 해석 영역의 경계면이 해석 결과에 미치는 영향을 최소화하기 위해(S. B. Suh et al. [9]) 해석 영역의 크기를 길이 방향은 덕트 직경의 10배, 폭 방향은 덕트 직경의 6배로 설정하였다. 프로펠러와 덕트, 스월 스테이터의 복잡한 형상 및 좁은 간격으로 인해 정렬 격자(Structured Mesh) 생성이 어렵기 때문에, 전체적으로는 사면체 비정렬 격자(Tetrahedral Unstructured Mesh)를 이용하여 격자를 생성하였고 각 물체의 벽면에는 경계층(Boundary Layer) 유동을 모사하기 위한 Prism Layer를 설정하였다.
Computational domain and boundary conditions
경계 조건은 유동 입구에 Velocity Inlet으로 설정하여 추진기로 유입되는 유속을 입력하였고, 유동 출구는 Pressure Outlet, 상/하/좌/우/ 방향 경계면은 자유류(Free Stream)를 모사할 수 있는 Slip Wall(Shear Stress = 0)로 설정하였다.
유동해석 상에서 프로펠러의 회전운동을 구현하는 방법에는 Sliding Mesh와 MRF(Moving Reference Frame)가 있다. Sliding Mesh는 프로펠러 주위의 격자계를 직접 회전시키는 방법이고, MRF는 격자계는 고정시킨 상태에서 상대속도 개념을 도입하여 좌표계를 회전시키는 방법이다. Sliding Mesh는 프로펠러 회전 시 주위 구조물과의 상대적인 위치에 의한 영향을 정확하게 반영할 수 있으나 반드시 비정상상태 해석(Transient Analysis)을 수행해야 하므로 계산 시간이 오래 걸린다는 단점이 있다. MRF는 반대로 정상상태 해석(Steady State Analysis)으로 수행이 가능하므로 계산 시간이 짧지만, 구조물과의 상대적인 위치에 의한 영향 반영이 제한적이다. M. G. Kim et al. [10]은 Sliding Mesh와 MRF 기법에 의해 Pod 프로펠러의 단독성능 분석을 수행하였는데, 2가지 방법에 의한 결과가 서로 흡사하게 도출되었다. 일반적으로 프로펠러 전후에 구조물이 없어 유동이 균일하거나 구조물이 있더라도 프로펠러와의 상대 위치에 따른 영향이 작다고 판단되는 경우에 정상상태 추진성능 예측을 위해서는 MRF 기법을 적용하는 것이 훨씬 효율적이고 정확도도 높은 편이다. 반면 프로펠러와 주위 구조물의 상대 위치에 따른 영향이 크다고 판단되거나 시간에 따른 유동특성의 Fluctuation을 파악하는 것이 중요한 경우에는 Sliding Mesh 기법을 적용하여야 한다. 본 연구에서는 프로펠러 앞에 장애물이 없으므로 균일한 반류가 유입되고 프로펠러 후방에 위치한 스월 스테이터도 프로펠러 날개에 비해 개수가 많으므로 상대 위치에 따른 영향이 작다고 판단하였으며, 정상상태에서의 추진성능을 확인하는 것이 목적이기 때문에 MRF 기법을 적용하여 프로펠러의 회전을 구현하였다. MRF는 프로펠러 주위의 유체 영역에만 적용하여 계산하고자 하는 추진기 회전속도(rpm)를 입력하였고, 나머지 영역은 회전속도가 없는 고정좌표계로 설정하였다(Figure 7).
MRF (Moving Reference Frame) Zone Setting
본 연구에서는 추진장치의 추력/토크/효율 곡선을 도출하기 위해 추진기로 유입되는 유속(VA)을 7.7m/s로 고정하고 추진기 회전수를 변화시켜 가면서 해석을 수행하였다. 캐비테이션 해석 시에는 프로펠러 주위의 기준 압력(Reference Pressure)이 캐비테이션 발생 여부를 결정하는 매우 중요한 인자로서, 기준 압력이 낮을수록 캐비테이션 발생 가능성이 높아진다. 수중에서의 기준 압력은 수심에 의해 결정되는데, 10m 내려갈 때마다 압력이 약 1bar 씩 증가한다. 본 연구에서는 캐비테이션이 발생할 가능성이 높은 수심 5m에서의 압력을 캐비테이션 해석 시 기준 압력으로 설정하였다. 작동 유체로는 해수(Sea Water)와 수증기(Water Vapor)를 적용하였다. 본 연구의 해석 경계 조건 및 물성치는 Table 2에 표시하였다.
Boundary conditions and properties
4. 해석 결과
수중 추진장치의 성능 분석을 위한 무차원 값인 전진비(JA, Adavance Ratio), 추력 계수(Kt, Thrst Coefficient), 토크 계수(Kq, Torque Coefficient), 단독효율(η0, Open Water Efficiency), 캐비테이션 수(σ, Cavitation Number)의 정의는 다음과 같다.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
여기서 VA는 프로펠러에 유입되는 유속, n은 프로펠러의 초당 회전수(rps), D는 프로펠러 직경, T는 추력, Q는 토크, pref는 주위 유동의 기준 압력, pv는 증기압을 나타낸다.
4.1 격자 테스트 및 해석 모델 검증
본 연구에서의 해석 모델을 검증하기 위하여 No. 19A 덕트를 장착한 Ka4-70(P/D = 1.4) 프로펠러에 대해 캐비테이션을 고려하지 않은 조건에서의 CFD 해석을 수행하였다. 검증용 Ka4-70 프로펠러의 직경은 본 연구에서 설계된 림 구동 추진장치와 동일한 380mm이며, 공개된 실험 데이터와 직접 비교할 수 있도록 No. 19A 덕트 형상을 변경하지 않고 적용하였다(Figure 5 (a)).
Open water test results of Ka4-70 screw series with nozzle No. 19A
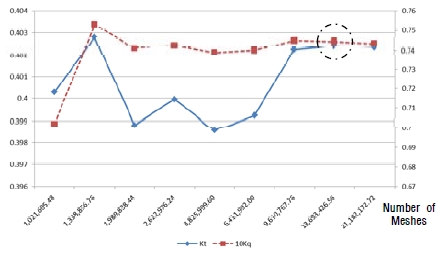
우선 적절한 격자 크기/개수를 결정하기 위한 격자 테스트를 수행하였다. 격자 크기/개수가 다른 조건에서 유속 7.7m/s, 회전수 1800rpm 일 때의 추력 계수 및 토크 계수를 계산한 결과, 격자수 약 1,370만 개(프로펠러 날개면의 평균 y+≒50)에서 안정적인 경향을 보이는 것으로 판단할 수 있었다(Figure 9).
The results of mesh test at JA=0.6768
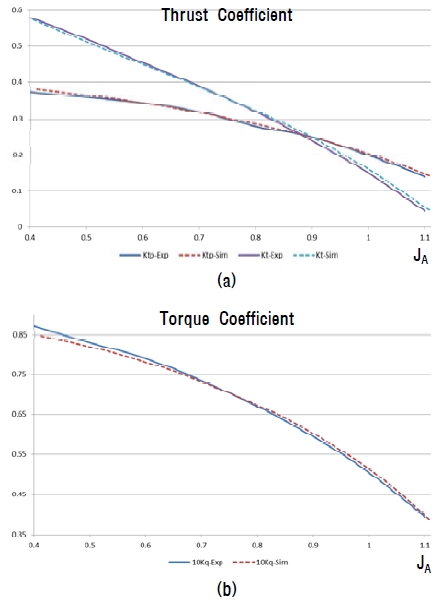
격자 테스트와 동일한 조건으로, 회전수 1100~3000rpm 범위에서 전진비(JA)에 따른 추진장치의 성능 곡선을 도출하고 Figure 8의 실험 데이터와 비교를 통한 해석 모델 검증을 수행하였다. CFD 해석으로 도출된 프로펠러 날개만의 추력 계수(Ktp), 추진장치 전체 추력 계수(Kt), 추진장치 전체 토크 계수(Kq) 곡선은 실험값과 거의 유사한 경향을 나타내고 있다(Figure 10). 이러한 결과를 기반으로 해석 모델 검증 시 적용했던 격자 및 경계조건을 이후에 수행한 CFD 해석에 동일하게 적용하였다. 이 때 총 격자수는 약 1,600만 개이다.
Experimental vs simulation results of Ka4-70 propulsor, which has original No. 19A duct
4.2 덕트 및 스월 스테이터에 의한 영향 분석
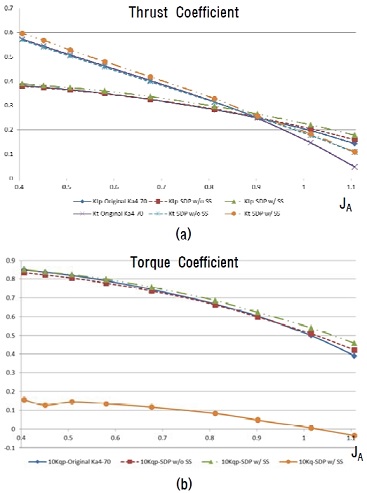
림 구동 추진장치의 성능분석을 수행하기에 앞서, 수정된 형상의 덕트와 스월 스테이터에 의한 영향을 확인하고자 기존 축 구동 추진장치에 대하여 Figure 5 (a), Figure 5 (b), Figure 5 (c) 3가지 형상에 대한 캐비테이션을 고려하지 않은 조건에서의 유동해석을 수행하였다. 수정된 덕트 형상 적용 시 높은 전진비(JA), 즉 낮은 회전수에서 전체 추력이 증가하며 프로펠러 날개 토크도 약간 증가하는 경향을 보인다. No. 19A 덕트는 낮은 전진비(JA)에서 전방의 압력 강하에 의해 큰 추진력을 얻을 수 있도록 설계되어 있는데, 높은 전진비(JA)에서는 전방의 압력 강하가 작기 때문에 반대로 큰 저항이 걸리게 된다. 반면 수정된 덕트 형상에서는 덕트 외부 프로파일이 평형하므로 높은 전진비(JA)에서의 저항이 상대적으로 작고, 내경의 중앙평행 구간이 길기 때문에 유입류의 균일도가 높아진다. 이러한 편차는 전진비(JA)가 낮아지면서 프로펠러 날개의 흡입력이 증가함에 따라 점차 감소하며, 오히려 낮은 전진비(JA)에서는 No. 19A 덕트 적용 시의 추력 및 토크가 약간 더 높게 나타난다. 스월 스테이터 적용 시에는 프로펠러 날개의 추력 및 토크, 전체 추력이 약간 증가하는데, 이는 프로펠러 날개 후류의 회전에너지 손실 감소와 스월 스테이터 자체에 추진력 방향으로 작용하는 힘의 영향인 것으로 판단된다. 또한 스월 스테이터가 프로펠러 날개에 의해 발생하는 롤 불균형을 상당 부분 상쇄시키며, 전진비(JA) 1.0 부근에서는 거의 롤 균형을 이루게 된다. Figure 11에서 Original Ka4-70은 수정되지 않은 No. 19A 덕트를 적용한 추진장치, SDP w/o SS는 수정된 형상의 덕트를 적용하고 스월 스테이터가 없는 추진장치, SDP w/ SS는 수정된 형상의 덕트를 적용하고 스월 스테이터가 있는 추진장치를 각각 의미한다.
Comparison of simulation results according to duct shape and existence of swirl stator (a) thrust coefficient (b) torque coefficient
4.3 림 구동 추진장치 단독성능 예측
캐비테이션을 고려하지 않은 조건에서 허브가 있는 경우와 없는 경우에 대하여 림 구동 추진장치의 단독성능 예측을 위한 유동해석을 수행하였고, 기존 축 구동 추진장치와의 비교 분석을 수행하였다. 림 구동 추진장치와 기존 축 구동 추진장치는 모두 수정된 덕트 형상과 스월 스테이터를 갖는 모델을 적용하였다.
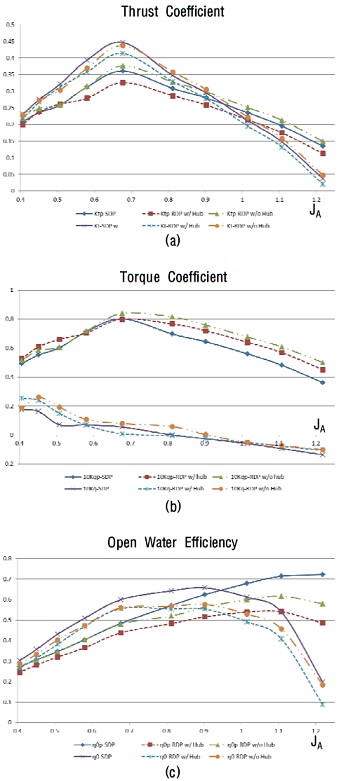
Table 3과 Figure 12는 스월 스테이터가 부착된 축 구동 추진장치(SDP)와 림 구동 추진장치(RDP)의 추력/토크 계수 및 효율을 나타낸 것이다. Ktp, Kqp, η0p는 프로펠러 날개(림 포함)만의, Kt, Kq, η0는 프로펠러 날개 뿐만 아니라 덕트/허브/스월 스테이터 등 프로펠러 전체의 추력/토크 계수 및 효율을 의미한다.
Open water performance of conventional shaft-driven propulsor and rim-driven propulsor with swirl stator in condition of non-cavitating flow
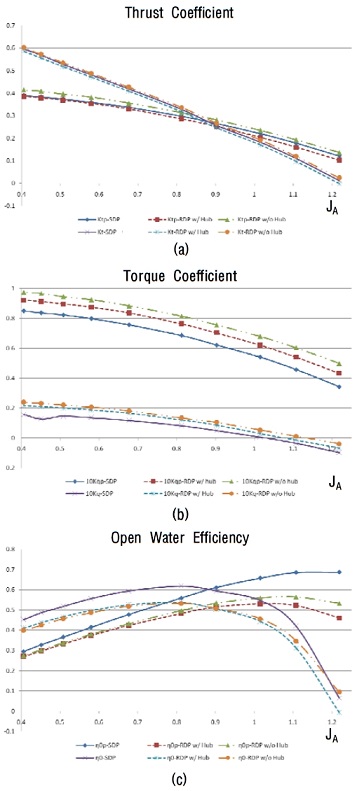
Comparison of open water performance between conventional shaft-driven propulsor and rim-driven propulsor with swirl stator in condition of non-cavitating flow (a) thrust coefficient (b) torque coefficient (c) open water efficiency
허브가 있는 림 구동 추진장치(RDP w/ Hub)의 경우 축 구동 추진장치에 비해 추력은 감소하고 토크는 증가하여 결과적으로 효율이 저하되는 경향을 보였다. 추력 감소는 프로펠러 날개 끝단에 부착되어 있는 림이 유동저항의 역할을 하기 때문이고, 토크 증가는 림이 프로펠러 날개와 함께 회전하므로 림 표면의 마찰항력이 모멘트로 작용하기 때문이다. 그러나 전진비(JA)가 작아질수록 림의 마찰효과에 의해 프로펠러 날개 끝단을 포함한 전체적인 영역에 걸쳐 유입 유속이 감소하여 받음각이 증가함에 따른 추력 증가 효과가 발생하므로, 추력 감소폭이 줄어드는 경향을 보인다. 허브가 없는 림 구동 추진장치는(RDP w/o Hub) 추력과 토크 모두 증가한다. 허브가 없기 때문에 덕트 내부에 유동이 흐를 수 있는 면적이 넓어지고, 특히 허브가 있던 부분과 그 근처에서의 유속이 증가함에 따라 대부분의 영역(r/R>0.3)에서는 상대적으로 프로펠러 단면으로 유입되는 유속이 감소하여 받음각이 커진다(Figure 13). 따라서 프로펠러 날개에 의해 발생하는 추력은 허브가 있는 경우보다 증가하고 림에 의한 추력 감소에도 불구하고 축 구동 추진장치보다 추력이 증가하는 효과를 나타내며, 토크도 같은 원리로 증가하게 된다. 그러나 유입 유속의 감소로 인한 덕트로 인한 추력은 감소하게 되고 스월 스테이터 후방의 압력 강하로 인한 저항 증가 효과 때문에(Figure 14), 전체 추력 증가폭은 프로펠러 날개 추력의 증가폭에 비해 작다. 또한 추력이 증가하는 것 이상으로 프로펠러 날개 토크가 증가하기 때문에, 전진비가 낮을 때는 허브가 없는 경우의 효율이 높지만 전진비가 높아질수록 효율이 비슷해지거나 오히려 허브가 있는 쪽이 높아지기도 한다. 전반적으로 효율은 축 구동 추진장치>허브가 없는 림 구동 추진장치>허브가 있는 림 구동 추진장치의 순서로 나타나지만, 전진비(JA)가 작아질수록 그 편차가 줄어드는 경향을 보이며, 특히 림 구동 추진장치의 허브 유무에 따른 편차는 거의 없어진다. 단, 선체 후부에 장착된 상태에서도 동일한 경향이 나타날 지 여부에 대해서는 추가적인 연구가 필요할 것이다.
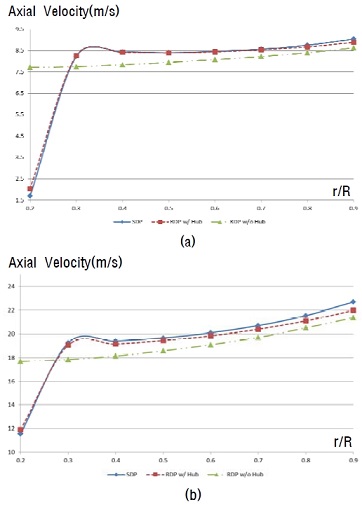
Axial velocity distribution at the point of 70mm ahead according to radius ratio in condition of non-cavitating flow (a) JA=1.2183 (b) JA=0.4061
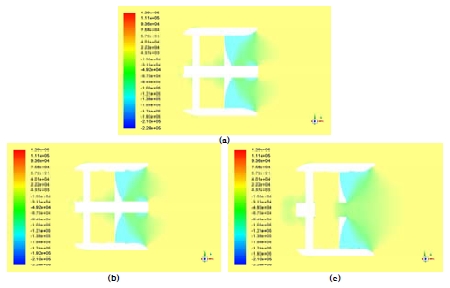
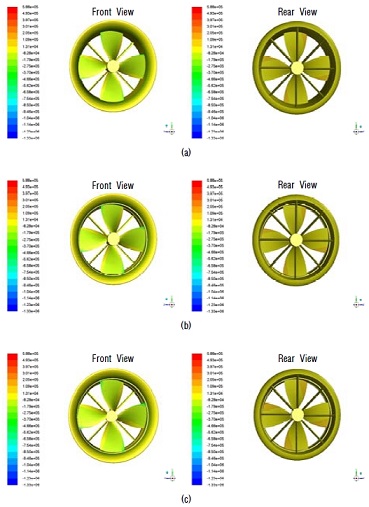
Static pressure distribution of fluid around propulsor at JA=0.6768 in condition of non-cavitating flow (a) shaft-driven propulsor with swirl stator (b) rim-driven propulsor with swirl stator and hub (c) rim-driven propulsor with swirl stator and without hub
Figure 13은 프로펠러 날개 중심으로부터 전방 70mm 지점에서 반경에 따른 축방향 유입 유속을 나타낸 것이고 Figure 14는 추진장치 주위 유체의 압력, Figure 15는 추진장치 벽면(프로펠러 날개, 덕트, 허브, 스월 스테이터)의 압력을 나타낸 것이다.
Pressure distribution of propulsor wall at JA=0.6768 in condition of non-cavitating flow (a) shaft-driven propulsor with swirl stator (b) rim-driven propulsor with swirl stator and hub (c) rim-driven propulsor with swirl stator and without hub
수심 5m에서의 수압(=150kPa)을 기준 압력으로 설정했을 때 캐비테이션을 고려한 조건에서의 추진장치 단독성능 해석을 수행하였다. Table 4와 Figure 16은 축 구동 추진장치(SDP)와 림 구동 추진장치(RDP)의 추력/토크 계수 및 효율을 나타낸 것이다. 효율은 축 구동 추진장치>허브가 없는 림 구동 추진장치>허브가 있는 림 구동 추진장치의 순서이며, 전반적인 추력과 토크 계수의 변화 경향 역시 캐비테이션을 고려하지 않은 조건에서의 해석과 거의 유사하게 나타나고 있다. 다만, 특정값 이하의 전진비(JA)에서는 캐비테이션이 과도하게 발생하여 추력/토크 계수가 오히려 감소하는 경향을 보여주고 있다. 롤 평형을 이루는 전진비(JA)는 캐비테이션을 고려하지 않은 조건에 비해 약간 낮아지는데, 이는 스월 스테이터의 뒷면에도 캐비테이션이 발생하기 때문인 것으로 판단된다.
Open water performance of conventional shaft-driven propulsor and rim-driven propulsor with swirl stator in condition of cavitating flow
Comparison of open water performance between conventional shaft-driven propulsor and rim-driven propulsor with swirl stator in condition of cavitating flow (a) thrust coefficient (b) torque coefficient (c) open water efficiency
Figure 17, Figure 18, Figure 19는 각각 다른 전진비(JA)와 캐비테이션 수(σ) 조건에서 증기(Vapor) 체적 분율(αv)이 0.5인 등고면(Iso-surface)을 통해 캐비테이션 발생 양상을 나타낸 것이고, Table 5는 캐비테이션에 의해 발생된 수증기의 양을 나타낸 것이다. 프로펠러 날개 중 유동을 빨아들이는 방향인 흡입면(Suction Side)에서 압력강하로 인해 캐비테이션이 발생하는 모습과 회전수 증가에 의해 캐비테이션 수(σ)가 감소함에 따라 캐비테이션 발생량이 증가하는 현상을 잘 보여주고 있다.
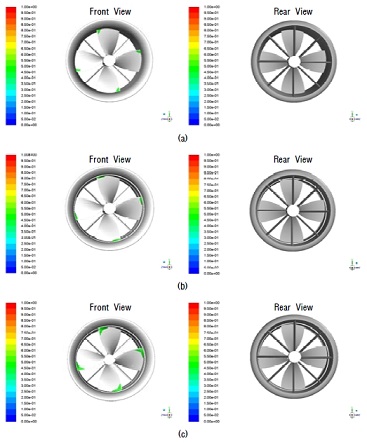
Iso-surface of vapor volume fraction (αv)=0.5 at JA=0.8122 and σ=3.2067 (a) shaft-driven propulsor with swirl stator (b) rim-driven propulsor with swirl stator and hub (c) rim-driven propulsor with swirl stator and without hub
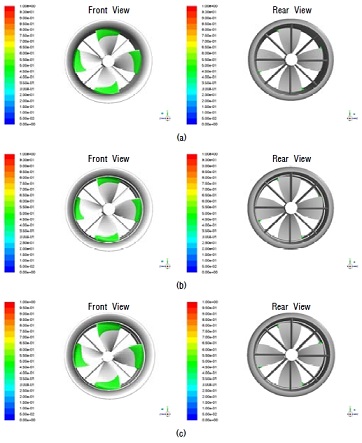
Iso-surface of vapor volume fraction (αv)=0.5 at JA=0.6768 and σ=2.2269 (a) shaft-driven propulsor with swirl stator (b) rim-driven propulsor with swirl stator and hub (c) rim-driven propulsor with swirl stator and without hub
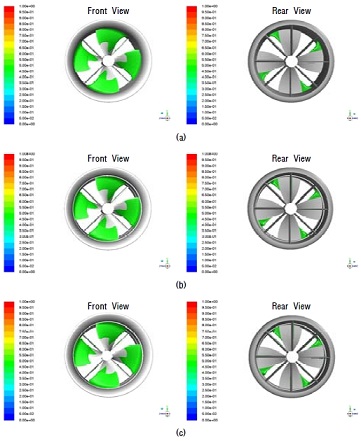
Iso-surface of vapor volume fraction(αv)=0.5 at JA =0.5082 and σ=1.6361 (a) shaft-driven propulsor with swirl stator (b) rim-driven propulsor with swirl stator and hub (c) rim-driven propulsor with swirl stator and without hub
Cavitation number (σ) and mass of water vapor in condition of cavitating flow
림 구동 추진장치는 축 구동 추진장치에 비해 더 낮은 회전수, 즉 더 높은 캐비테이션 수(σ)에서 캐비테이션이 발생하기 시작하며 수증기 발생량도 더 많은 경향을 보인다. 특히 허브가 없는 림 구동 추진장치에서 캐비테이션이 더 많이 발생된다. 이는 “4.3.1” 에서 설명한 바와 같이 프로펠러 날개로 유입되는 유속의 차이로 인해 받음각이 증가하게 되고(Figure 13) 흡입면의 압력 강하가 더 커지기 때문이다. 다만 캐비테이션 수(σ)가 1 이하로 내려가는 시점에서는 축 구동 추진장치의 수증기 발생량이 더 많아지는 경향을 보이는데, 이는 날개 끝(Tip)에서 발생하는 캐비테이션에 의한 것으로 추정된다. 또한 림 유무에 따라 초기 캐비테이션 발생 양상이 달라진다. 림이 없는 경우에는 Leading Edge 쪽에서 초기 캐비테이션이 발생하나, 림이 있는 경우에는 날개 끝단에서 많이 발생하게 되고, 특히 허브가 없는 경우에는 받음각의 증가로 인해 Leading Edge 쪽으로도 좀 더 넓게 확산되는 경향을 보여주고 있다.
5. 결 론
본 연구에서는 기존의 축 구동 추진장치 대비 림 구동 추진장치의 유체역학적 특성을 확인하기 위한 CFD 해석을 수행하였다. Ka4-70 프로펠러 날개 형상과 No. 19A 기반으로 수정된 형상의 덕트를 갖는 림 구동 추진장치를 설계하였고, 캐비테이션을 고려하지 않은 조건과 수심 5m 조건에서 캐비테이션을 고려한 조건에 대해서 추력/토크 계수, 단독효율 등 선체에 장착되지 않은 상태에서의 단독성능과 캐비테이션 발생 양상을 예측하였다. 그 결과 다음과 같은 결론을 얻을 수 있었다.
- (1) No. 19A를 기반으로 수정된 형상의 덕트와 스월 스테이터는 추진성능을 저하시키지 않으며, 오히려 추력을 약간 증가시키는 효과가 있다. 스월 스테이터는 프로펠러 날개에 의해 발생하는 롤 불균형을 상당부분 상쇄시킨다.
- (2) 허브가 있는 림 구동 추진장치는 프로펠러 날개 끝단의 림이 저항으로 작용하고 프로펠러 날개와 함께 회전함에 따른 마찰력이 부가 토크로 작용하여, 동일한 제원의 축 구동 추진장치에 비해 추력은 감소하고 토크는 증가하여 효율이 낮아진다. 즉, 동일한 추력을 내기 위해서는 더 높은 회전수가 필요하고 더 큰 모터 출력이 필요하게 된다.
- (3) 허브가 없는 림 구동 추진장치는 프로펠러 날개로 유입되는 유동의 받음각이 커지는 효과로 인하여 추력이 증가하지만 토크가 더 큰 비율로 증가하기 때문에, 역시 효율은 낮아진다. 동일한 추력을 내기 위한 회전수는 낮아지지만 모터 출력은 증가하는 것이다.
- (4) 추진장치의 회전수가 증가함에 따라 캐비테이션이 과도하게 생성되면, 추력/토크 계수가 급격하게 감소하는 현상이 발생한다.
- (5) 림 구동 추진장치는 축 구동 장치에 비해 더 낮은 회전수(더 높은 캐비테이션 수)에서 캐비테이션이 발생하고 발생량도 더 많은 경향을 보이며, 허브가 없는 경우에 이러한 현상이 더 크게 나타난다. 이는 역시 프로펠러 날개로 유입되는 유동의 받음각이 커지는 효과에 의한 것으로 판단된다. 림과 허브의 유무에 따라 초기 캐비테이션 발생 양상 또한 다르게 나타난다.
향후 림 구동 추진장치가 실용화되기 위해서는, 추진효율을 향상시키고 캐비테이션 발생을 최소화할 수 있는 최적화 설계에 대한 연구가 수행되어야 할 것이며, 특히 허브가 없는 타입의 경우에는 허브가 있던 공간을 활용한 설계 방안에 대한 검토가 이루어져야 할 것으로 생각된다. 본 연구의 결과는 기존의 축 구동 추진장치 대비 림 구동 추진장치의 유체역학적 특성과 추진성능의 변화를 사전에 예측하고 최적화 설계를 수행하기 위한 기초자료로 활용될 것이며, 최종적으로는 선체에 장착된 상태에서의 분석을 통해 림 구동 추진장치를 장착한 무인잠수정의 추진성능을 도출할 예정이다.
Author Contributions
The following statements should be used “Conceptualization and Methodology, J. H. Park; Survey of Previous Research, J. H. Park and S. J. Ha; Concept Design and General Arrangement of Propulsor, J. Y. Choi; Propeller Blade Design, J. H. Park; Duct Design, Y. H. Jeon; Swirl Stator Design, S. J. Ha; Performing CFD Simulations, Je. H. Park; Verifying CFD Simulations, S. J. Ha; Data Analysis, J. H. Park and Y. H. Jeon; Writing—Original Draft Preparation, J. H. Park; Writing—Review & Editing, J. Y. Choi”.
References
-
K. B. Kim, M. H. Lee, S. M. Lee, and G. H. Jang, “Optimal design and experimental verification of fluid dynamic bearings with high load capacity applied to an integrated motor propulsor in unmanned underwater vehicles”, Tribology International, 114, p221-233, (2017).
[https://doi.org/10.1016/j.triboint.2017.04.017]
- H. R. Yu, Y. R. Jung, and Y. G. Park, “Numerical flow analysis of ducted marine propeller with pre-swirl guidevane”, Journal of Computational Fluids Engineering, 9(2), p62-69, (2004), (in Korean).
-
T. H. Joung, S. J. Jeong, and S. K. Lee, “CFD simulations and experimental tests for three different ducted propellers”, Journal of Ocean Engineering and Technology, 28(3), p199-208, (2014), (in Korean).
[https://doi.org/10.5574/KSOE.2014.28.3.199]
- S. B. Suh, “CFD analysis of performance of KRISO devices (K-DUCT) for propulsion efficiency improvement”, Journal of Ocean Engineering and Technology, 31(3), p183-188, (2017), (in Korean).
-
J. I. Kim, I. R. Park, K. S. Kim, and J. W. Ahn, “Numerical analysis of non-cavitating and cavitating performance of a SVA potsdam propeller”, Journal of the Society of Naval Architects of Korea, 54(3), p215-226, (2017), (in Korean).
[https://doi.org/10.3744/SNAK.2017.54.3.215]
- ANSYS Inc., ANSYS Fluent Theory Guide 19.2, (2018).
-
J. S. Carlton, Marine Propellers and Propulsion, 2nd ed., Elsevier, (2007).
[https://doi.org/10.1016/b978-0-7506-8150-6.x5000-1]
- G. H. Schnerr, and J. Sauer, “Physical and numerical modeling of unsteady cavitation dynamics”, Proceedings of Fourth International Conference on Multiphase Flow, p1-12, (2001).
-
S. B. Suh, and K. S. Kim, “Study on the wall effect correction for propeller open water characteristics in the medium size cavitation tunnel”, Journal of the Korean Society of Marine Engineering, 34(5), p718-724, (2010), (in Korean).
[https://doi.org/10.5916/jkosme.2010.34.5.718]
-
M. G. Kim, H. T. Ahn, J. T. Lee, and H. G. Lee, “Fully unstructured mesh based computation of viscous flow around marine propellers”, Journal of the Society of Naval Architects of Korea, 51(2), p162-170, (2014), (in Korean).
[https://doi.org/10.3744/SNAK.2014.51.2.162]