2.5MW급 발전용 증기터빈의 회전체동역학해석 및 방사소음해석

1. 서 론

증기터빈(steam turbine)은 고온, 고압의 증기가 보유한 열에너지를 활용하여 기계적인 일을 생산하는 열기관이다. 현재 증기터빈은 회전동력을 필요로 하는 기계장치, 전기를 생산하는 발전설비 등 다양한 산업분야에서 활용되고 있다. 회전력을 활용하는 동력장치 및 발전설비에 있어서 회전기계(rotating machinery)는 그 역할이 아주 중요하다. 따라서 초기 설계단계에서부터 회전체의 불안정한 거동을 예측하고 개선사항을 반영하여 목표와 요구사항을 만족하는 설계를 수행할 수 있어야 한다.

증기터빈을 구성하는 회전기계는 크게 회전축(rotating shaft), 회전디스크(rotary disk), 회전날개(rotary blade)로 구성되어 있고 이들 각각의 특성과 연성관계가 고려된 복잡한 구조를 갖는다. 특히 중소형 터빈발전기의 경우 소형화와 고출력의 조건을 충족시키기 위해 높은 회전속도에서 운전됨과 동시에 많은 유량을 수용하여야 하므로 비슷한 크기의 기계구조에 비해 큰 내부부하가 존재하고 이로 인해 동적안정성(dynamic stability) 측면에서 치명적인 문제가 발생할 수 있다. 따라서 설계 초기단계부터 회전체에 대한 회전체동역학 해석을 수행하여 공진이 발생하는 위험속도(critical speed)와 운전조건에서의 진동응답을 예측하여 안정성을 판단할 수 있어야 한다.

한편 증기터빈은 고속으로 회전하는 회전체를 포함하며 고온-고압의 동작 유체를 수용하므로 많은 소음이 발생하게 된다. 특히 중소형 증기터빈발전기의 경우 수요자 인근에 위치하게 되어 작업자의 근무환경 및 거주자의 생활환경에 좋지 않은 영향을 끼치게 된다. 따라서 설계단계에서 소음원에 대한 규정 및 방사소음을 예측하고 그 결과를 바탕으로 경제적인 소음저감 대책을 수립하여야 한다.

이러한 이유들로 회전기계의 동적안정성을 확보하기 위한 다양한 연구가 진행되었다. [1]에서는 소형 가스터빈 회전체의 위험속도를 예측하기 위한 연구를 수행하였고, [2]에서는 소형 가스터빈 회전체의 진동응답을 예측하기 위한 연구를 수행하였다. [3]에서는 베어링지지 효과를 고려한 회전체동역학 해석을 수행하였으며 회전기계의 유한요소 모델링 방법에 대한 특성을 제시하였다. [4]에서는 10MW급 초임계 발전용 축류 터빈에 대해 회전체동역학해석을 수행하고 설계 건전성을 검토하였다. 수요자 인근에서 소음을 발생시키는 기계류에 대한 방사소음예측에 대한 연구도 꾸준히 진행되었다. [5]에서는 식기세척기의 구조기인 방사소음을 저감하기 위한 연구를 수행하였다. [6]에서는 수치해석기법을 활용하여 엔진의 방사소음을 예측하는 연구를 수행하였다. 이외에도 많은 연구가 진행되었지만 발전용 터빈에 대해 회전체동역학 해석을 수행하고 그 동적 응답 결과를 활용하여 방사소음해석을 수행한 연구는 수행된 바가 없었다.

본 연구에서는 2.5MW급 발전용 증기터빈의 설계 초기단계에서 진동소음성능을 확보하기 위해 이루어지는 해석을 수행하고 그 프로세스를 제시하는 것을 목적으로 한다. 이를 위해 회전체 동역학 해석을 수행하여 터빈을 구성하는 회전기계의 운전안정성을 평가 하였다. 또한 회전기계와 케이싱 구조물의 상호작용에 의해 발생하는 방사소음을 예측하기 위해 베어링 위치에서 회전기계의 진동응답 값을 가진원으로 하여 터빈 케이싱의 방사소음해석을 수행하였다. 회전체 동역학 해석 및 방사소음해석에는 각각 상용프로그램인 SIEMENS사의 SAMCEF 와 Simcenter 3D를 활용하였다.

2. 회전체 동역학해석

2.1 수치해석모델 생성

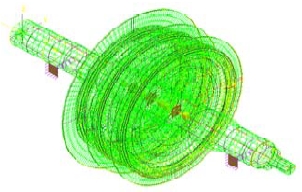
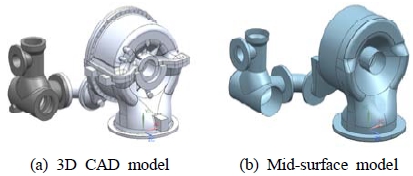
일반적으로 해석대상의 전체 동특성(global dynamic characteristics)을 효과적으로 파악하기 위한 수치해석을 수행할 때 실제 구조물의 복잡한 국부형상을 단순화하여 수치적 모델로 적합하게 수정하는 작업이 필수적으로 요구된다. 따라서 Figure 1 (a)의 회전체 형상에서 불필요하게 해석모델의 크기를 증가시키거나 요소의 질(quality of element)을 저하시킬 수 있는 부분을 적절히 필터링하여 Figure 1 (b)와 같이 등가모델(equivalent model)을 생성하였다.

Figure 1:

Geometric configuration for a rotating system of a steam turbine

3D CAD모델 및 등가화모델의 질량(mass), 질량관성모멘트(mass moment of inertia) 등의 동적특성에 관한 변수들은 Table 1과 같다.

Table 1:

Enforced displacement condition

Figure 1 (b)의 회전체 등가화모델을 바탕으로 육면체요소(hexahedron element) 및 오면체요소(pentahedron element)를 활용하여 Figure 2와 같이 유한요소모델(finite element model)을 생성(요소수 9,701개, 노드수 15,814개)하였다.

Figure 2:

FE model for a rotating system of a steam turbine

본 연구에서는 조립부의 국부적인 구조 안정성이 아닌 설계 초기단계에서 요구되는 회전체의 위험속도 및 불균형응답(unbalance response)과 같은 전체적인 동적특성을 파악하는 것이 목적이다. 따라서 유한요소모델을 생성할 때 회전체 조립부의 연결은 견고히 된 것으로 가정하여 조립부의 접촉면을 구성하는 노드들은 SAMCEF의 Glue기능을 활용하여 노드공유 하였다. 회전축과 베어링이 접하는 부분에 회전축의 수직평면상에 두 직교방향으로 베어링 조건을 부여하였다. 베어링 물성치는 설계 스펙대로 강성이 k_x = k_y = 1×10⁸ N/m인 베어링 조건을 적용하였다.

2.2 위험속도해석

위험속도란 회전체의 고유진동수에 해당하는 축의 회전속도이다. 회전체는 회전축이 위험속도로 회전할 때 공진모드가 발생하고 이로 인해 회전체의 불안정, 특히 베어링부의 피로누적에 의한 구조적 문제가 발생할 수 있다. 본 연구에서는 증기터빈을 구성하는 회전체의 불안정한 진동현상을 방지하고자 위험속도해석(critical speed analysis)을 수행하였다.

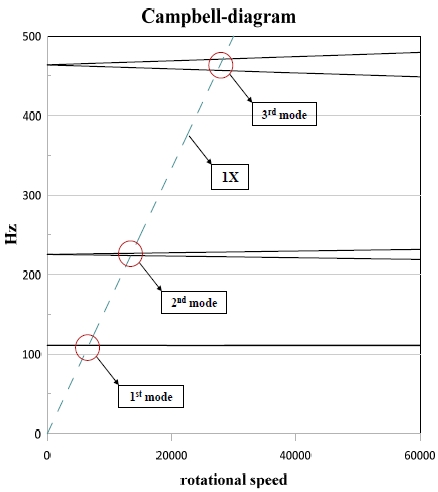
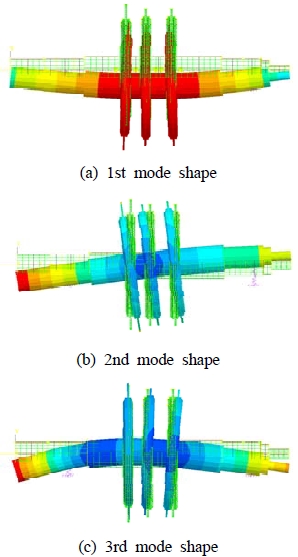
회전체의 고유진동수는 축의 회전속도에 따라 변화하기 때문에 회전체의 공진을 예측하는 방법으로 축의 회전속도에 따른 고유진동수를 표현해주는 Campbell diagram이 널리 활용된다. Figure 3의 Campbell diagram을 통해 회전속도에 따른 고유진동수의 분포를 확인할 수 있다. 회전체에 존재하는 질량불균형(unbalance mass)은 축의 회전속도에 따른 외력으로 작용하므로 1x-동기회전수 선과 교차되는 지점을 선정하여 위험속도를 예측할 수 있다. 일반적으로 위험속도는 정 선회 위험속도(forward critical speed)와 역 선회 위험속도(backward critical speed) 두 가지 다른 위험속도가 나타나는데 회전속도와 동일한 불균형 가진력은 정 선회 위험속도와 공진을 일으키기 때문에 정 선회 위험속도만을 고려하였다. 해석결과 1차 위험속도는 6,669rpm, 2차 위험속도는 13,578rpm, 3차 위험속도는 27,698rpm로 산출되었다. 각 위험속도에서의 모드형상은 Figure 4와 같다.

Figure 3:

Campbell diagram

Figure 4:

Mode shape of a rotor

2.3 불균형 응답해석

회전체에 존재하는 미세한 질량불균형(unbalance mass)은 고속으로 회전하는 증기터빈 회전체에 있어서 주요한 가진원이다. 따라서 회전체의 질량불균형이 고려된 불균형 응답해석(unbalance response analysis)을 수행하여 터빈의 정격운전속도 범위 내에 존재하는 위험속도 분포와 베어링 위치에서의 진동응답레벨을 검토하였다. 또한 진동응답레벨은 방사소음해석을 수행할 때 케이싱 구조에 입력되는 가진원으로 활용하였다.

해석을 수행함에 있어 실제 회전체의 질량불균형을 정확히 예측하는 것은 불가능하다. 따라서 해석에 활용할 최대 허용 불평형량은 식 (1)과 가정하였다[7].

$\[ U_{\text{max}}=1000•\frac{G•m}{\Omega }\left(\text{g⋅mm}\right) \]$

(1)

$\[ \Omega =\frac{2\times \pi \times N}{60}\left(\text{rad/sec}\right) \]$

(2)

식 (1)은 ISO 1940-1에서 규정하고 있는 최대 허용 불평형량이다. G는 밸런싱등급, m은 회전체의 질량(kg), N는 최대회전속도(m/s)이다.

본 연구에서는 G2.5등급에 해당하는 최대 허용 불평형량을 130g·mm과 같이 계산하였고 Figure 4 (a)의 1차 모드형상에서 큰 변위를 갖는 회전체 중앙에 부여하였다. 해석결과로 얻은 응답은 미국석유협회(API, American Petroleum Institute)에서 규정하고 있는 최대진동레벨인 식 (3)을 초과하지 않아야 한다[8][9].

$\[ L_v=25.4\sqrt{\frac{\mathrm{12,000}}{N}} \left(\mu m\right) \]$

(3)

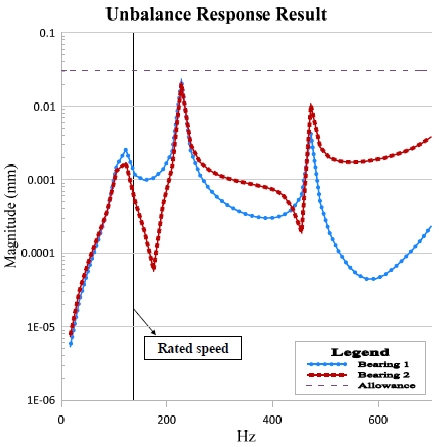
Figure 5의 불균형 응답해석 결과를 통해 관심영역 내의 피크응답에 기여하는 고유모드를 확인 할 수 있다. 또한 그 응답의 크기가 API의 규정에서 제시하고 있는 허용치를 초과하지 않음을 확인할 수 있다.

Figure 5:

Unbalance response analysis result

3. 케이싱 방사소음 해석

3.1 소음해석모델 생성

본 연구에서는 회전체동역학해석을 수행하여 얻은 불평형응답을 가진원으로 하여 터빈 케이싱의 구조기인 방사소음을 예측하는 구조-음향 연성해석을 수행하였다. 방사소음해석에는 상용프로그램인 Simcenter 3D의 FEM-AML방법을 활용하였다. 일반적으로 외부 방사소음문제에 유한요소법(FEM, finite element method)을 적용하기 위해서 외부음장에 인공경계면을 생성하고 Sommerfeld 방사조건의 구현을 위해 흡수경계조건(absorbing boundary condition)을 부여한다[10]. 이때 방사표면과 인공경계면 사이에 생성되는 유한한 공간 내부의 응답은 유한요소법에 의해 얻어지지만 경계면 외부에 위치하는 계측지점의 응답은 식 (4)과 같이 표현되는 Kirchhoff Helmholtz 적분식(integral equation)을 이용하여 얻을 수 있다[11].

$\[ p\left(x\right)={\int }_{\Gamma }^{}\left(G\left(x,y\right)\frac{\partial p\left(y\right)}{\partial n}+p\left(y\right)\frac{\partial G\left(x,y\right)}{\partial n}\right)\Gamma \]$

(4)

식 (4)에서 x는 경계면 외부에 위치하는 임의의 계측지점이고 y는 유한요소도메인의 외부경계면, Γ에 위치하는 임의의 지점이다. G(x,y)는 그린함수(Green function)이다.

본 연구에서는 흡수경계조건으로 AML (automatically matched layer)방법을 적용하였다. AML은 PML (perfectly matched layer)의 최적화된 형태로 해석이 수행되는 주파수영역에 따라 적절하게 흡수층의 두께를 조절하는 것으로 알려져 있다. 따라서 AML방법은 해석목표 주파수에 따라 알맞은 두께로 흡수층을 생성해야하는 PML방법에 비해 모델링의 편의성과 계산효율이 높다. 하지만 기본적으로 유한요소법을 활용하기 때문에 해석모델에 지면이나 벽면이 고려된다면 유한요소법이 적용되는 도메인의 크기가 확장됨에 따라 계산비용이 급격하게 증가할 수 있어 주의가 필요하다[11].

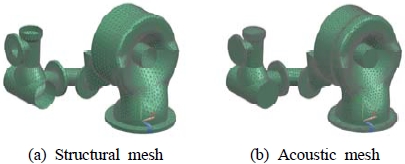
수치해석모델을 생성함에 있어 전체 해석시간을 줄이고, 목표 주파수 대역에서 방사소음 해석결과에 대한 케이싱의 상세한 형상정보는 기여도가 낮다고 판단되어 Figure 6과 같이 기존의 3D 형상의 중간면(mid-surface)을 이용한 2D 모델을 생성하였다. Figure 7 (a)는 구조 유한요소모델을 보여주며 12,120개의 요소와 6,062개의 노드로 구성되어 있다. Figure 7 (b)에 나타낸 구조요소 표면의 음향요소망(acoustic mesh)의 경우 최대 1000Hz까지 해석이 가능하도록 요소크기를 선정하였다.

Figure 6:

Geometric configuration for a casing of a steam turbine

Figure 7:

FE model

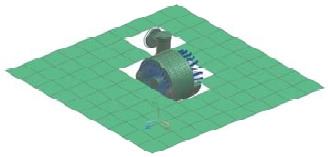
외부음장을 유한요소법으로 모델링하기 위해 Figure 8 (a)와 같이 방사표면에 근접한 위치에 Convex mesh를 생성하였다. 한편 실제 방사소음을 계측하거나 터빈이 운전될 때는 지면(ground)이 고려된 반무향조건(semi-anechoic condition)에서 이루어진다. 이러한 반무향 조건을 해석적으로 구현하기 위해 대칭면(symmetry plane)을 생성하였다. 또한 Figure 8 (b)와 같이 음향요소망과 Convex mesh 및 대칭면에 의해 생성된 유한한 음장은 96,140개의 사면체요소(tetrahedron element)를 이용하여 이산화하고 사면체요소로 이루어진 도메인의 외부 표면에 AML을 적용하였다.

Figure 8:

Exterior fluid mesh model

3.2 방사소음해석

본 연구에서는 터빈 케이싱 구조물의 구조기인 방사소음을 예측하기 위해 Table 2와 같이 회전축의 진동에 의해 터빈케이싱에 입력되는 가진변위량(enforced displacement)을 산출하였으며 Figure 9와 같이 회전축이 지지되는 부분에 부여하였다.

Table 2:

Enforced displacement condition

Figure 9:

Field point mesh and boundary conditions

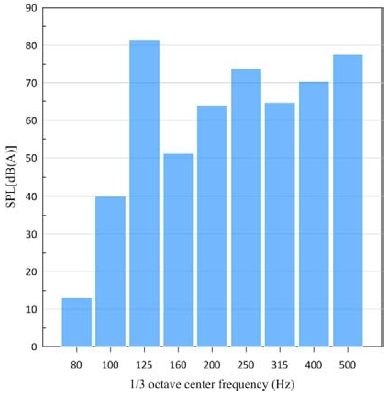
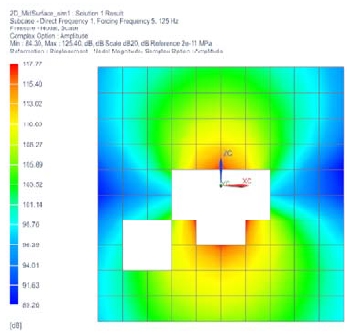
음압레벨(SPL, sound pressure level)을 확인하기 위한 microphone mesh는 KS B 6361 규격을 참고하여 방사표면을 기준으로 반경 1m의 4방위 지점에 생성하였다[12]. 또한 음압레벨의 분포를 확인하기 위한 field point plane mesh를 Figure 9와 같이 생성하였다. Figure 10은 터빈 케이싱의 진동소음연성해석을 수행한 결과이며 방사체 주위에 생성한 4지점의 microphone mesh를 통해 얻은 결과 값들의 평균치를 1/3옥타브밴드에서 표현(dBA)하였다. Figure 11은 125Hz에서 field point mesh 상에 표현된 음압레벨의 분포를 나타낸다. 증기터빈의 정격회전 속도에서 이루어지는 가진 성분인 140Hz에서의 구조기인 방사소음 음압레벨은 대략 81dBA, 전체 음압레벨은 83dBA로 예측되었다.

Figure 10:

Sound pressure level

Figure 11:

Sound pressure level on the field point mesh

4. 결 론

본 연구에서는 2.5MW급 발전용 증기터빈발전기를 구성하는 회전체에 대한 회전체 동역학해석을 수행하여 증기터빈 회전체의 신뢰성 및 안정성을 평가하였고, 증기터빈 회전체의 운전조건에 따른 진동응답 특성을 고려하여 케이싱 구조물의 방사소음해석을 수행하여 회전체와 케이싱 구조물의 상호작용에 의해 발생하는 방사소음레벨을 예측하였다.

회전체동역학해석으로는 증기터빈 회전체의 공진회피를 위한 위험속도해석과 운전 안정성 확보를 위한 불균형응답해석을 수행하였다. 해석결과 회전체의 위험속도 분포와 베어링 위치에서의 강제 가진응답을 확인할 수 있었다. 회전체의 질량불균형에 의해 베어링 부분에서 발생하는 진동응답의 경우 API에서 제시하는 허용치를 만족함을 확인하였다. 특히 정격회전속도 근처에 1차 위험속도가 존재하였지만 20%의 충분한 분리여유가 확보되어 설계안이 안정하다고 판단된다.

케이싱의 방사소음 해석결과 터빈이 운전될 때 회전축과 케이싱 구조물의 상호작용에 의해 발생하는 방사소음레벨을 확인하였다. 정격회전속도에서 발생하는 가진주파수인 135~140 Hz 근처에서의 음압은 약 81dBA, 전체음압레벨은 83dBA로 예측되며 본 모델의 개발목표치 90dBA에 만족하였다.

일반적으로 증기터빈에서 발생되는 소음원은 회전체와 케이싱의 상호작용에 의한 구조기인소음뿐만 아니라 고속으로 회전하는 회전자와 동작 유체의 마찰에 의한 소음, 흡기계 및 배기계에서 발생 가능한 소음 등 유체기인소음에 대한 부분이 고려되어야 한다. 따라서 좀 더 신뢰성 높은 터빈의 소음성능을 예측하기 위해서는 전산유체역학(computational fluid dynamics)을 활용한 유동해석을 통해 유동기인 소음원을 산정하고 이를 고려한 소음해석을 수행하는 추가적인 연구가 필요하다.

Acknowledgments

본 연구는 산업통상자원부와 한국산업기술진흥원의 “지역특화산업육성사업”으로 수행된 연구결과입니다. (R0006182)

References

• Y. C. Kim, J. W. Ha, and J. H. Myung, “Critical speed analysis of a small gas turbine rotor”, The KSFM Journal of Fluid Machinery, 12(3), p26-30, (2009), (in Korean). [https://doi.org/10.5293/KFMA.2009.12.3.026]
• Y. C. Kim, J. W. Ha, and J. H. Myung, “Vibration response analysis of a small gas turbine rotor”, The KSFM Journal of Fluid Machinery, 13(3), p18-23, (2010), (in Korean). [https://doi.org/10.5293/KFMA.2010.13.3.018]
• H. K. Park, D. H. Kim, D. M. Kim, Y. S. Kim, M. K. Kim, and S. B. Chen, “Three-dimensional rotordynamic analysis considering bearing support effects”, Transactions of the Korean Society for Noise and Vibration Engineering, 17(2), p105-113, (2007), (in Korean). [https://doi.org/10.5050/KSNVN.2007.17.2.105]
• D. H. Lee, B. O. Kim, H. S. Lim, M. R. Park, D. W. Kang, and B. S. Choi, “Rotordynamic characteristic analysis for axial turbine for the 10MW super-critical CO₂ cycle application”, The KSFM Journal of Fluid Machinery, 21(1), p13-18, (2018), (in Korean). [https://doi.org/10.5293/kfma.2018.21.1.013]
• H. W. Yoon, and S. K. Lee, “Analysis of influence of oil pan structure modification on radiation noise of an engine using FEM”, Transactions of the KSAE, 25(5), p573-580, (2017), (in Korean). [https://doi.org/10.7467/KSAE.2017.25.5.573]
• J. B. Han, J. H. Kang, K. W. Hong, G. S. Na, and D. U. Kang, “Prediction of structure-borne noise for a dishwasher”, Proceedings of the Korean Society for Noise and Vibration Engineering Conference, p125-126, (2015), (in Korean).
• ISO 1940-1, “Mechanical vibration – Balance quality requirements for rotors in a constant state – Part1: Specification and verification of balance tolerances”, Second edition, (2003).
• B. O. Kim, A. S. Lee, D. H. Lee, and Y. C. Kim, “Rotor dynamic analysis procedure for ensuring reliability of rotating machines”, Journal of Fluid Machinery and Systems, 10(5), p64-73, (2007), (in Korean). [https://doi.org/10.5293/KFMA.2007.10.5.064]
• A. S. Lee, “Overview of rotational dynamics design technology”, Transactions of the Korean Society for Noise and Vibration Engineering, 26(3), (2016), (in Korean).
• Frank Ihlenburg, Finite Element Analysis of Acoustic Scattering, Springer, (1998).
• K. Vansant, R. Hallez, H. Beriot, M. Tournour, G. Massa, S. Donders, and H. V. Auweraer, “Simulating acoustic engine performance over a broad frequency range”, SAE Technical Paper, (2011). [https://doi.org/10.4271/2011-26-0019]
• Korea Industrial Standard, “KS B 6361. Methods of A-weighted sound pressure level measurement or ans, compressors”, (2017).