A study on battery characteristics for electrical propulsion vessels according to charging current and harmonic discharging load

2.1 Parameter analysis

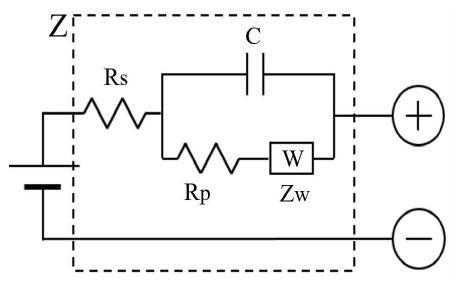
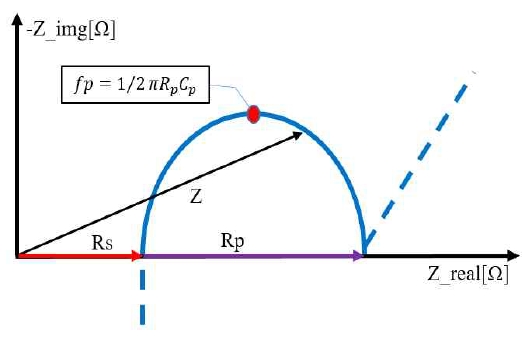
The electrochemical process inside a battery is represented by the simplified impedance model shown in Figure 1. Z represents the impedance of the battery and is divided by the real number R_real and the imaginary number R_imag in Figure 2. Rs is the resistance of the battery interior (electrode, electrolyte). Large voltage and current times dominate battery characteristics. This is also called AC resistance, measured at high frequencies. The Rs value increases as performance deteriorates because of battery aging. Therefore, it is common to measure the battery’s state-of-health (SoH). The relationship between Rs and SoH differs depending on the type and size of the battery. The method of continuously updating the correlation between Rs and SoH is applied while demonstrating evaluation criteria via preliminary examination of the same type of battery [5][6].

Figure 1:

Simplified battery impedance model

Figure 2:

Impedance according to frequency (Nyquist Diagram)

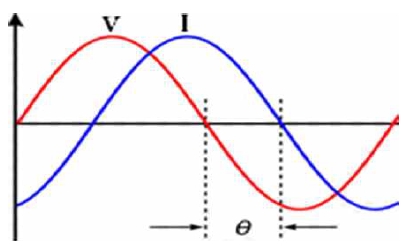
Rp represents the electrochemical reaction rate, and Cp represents the capacitor function of the electric double layer between the electrode and the electrolyte. Rp and Cp are criteria for indicating the state-of-charge (SoC) of the battery [7]. For a lithium battery, Rs is detected in the vicinity of 1 kHz. The relationship between the sinusoidal AC voltage and the response current is shown in Figure 3. The phase difference between battery current and voltage is denoted by θ, and the impedance relation is as follows:

Figure 3:

Sine-wave AC voltage and sinusoidal response current waveform

2.2 C-rate

For a battery with a capacity of 1 Ah, the reference-1 C-rate (expressed as C) is 1 A, and the amount of current is the capacity of the cell. The lithium secondary battery can charge and discharge several times, and can have different energy storage states depending on charge and discharge methods [6].

2.3 SoH (State of health)

A battery stores and delivers electrical power via an electrochemical process. The SoH represents a battery’s usable life (%). Battery-aging and deterioration processes are important concerns. Deterioration is affected by chemical, external environment, and electrical characteristics. Thus, it is very difficult to accurately grasp the value of SoH. The maximum usable capacity of the battery is closely related to SoH, and if the battery is reduced to 80% of the maximum usable capacity, it is considered unusable. Furthermore, as the battery is repeatedly charged and discharged, performance is reduced and life span is shortened [5][8].

2.4 SoC (State of Charge)

Unlike conventional primary batteries, a lithium secondary battery can charge and discharge many times. Thus, they have a variety of energy storage states. Capacity is defined as the total charge amount when discharged at a constant current from fully charged (SoC = 100%) to empty (SoC = 0%) [5][6].

3.1 Software

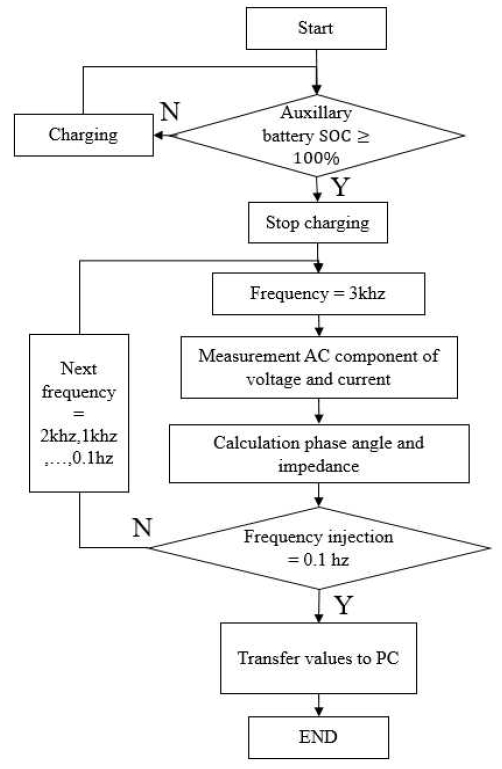
Figure 4 shows a flowchart for measuring the impedance of a microprocessor battery . If the SoC of the battery is 100 %, it is measured using the electrochemical impedance spectroscopy (EIS) technique. If conditions are not satisfied, charging is continued. Next, an initial frequency of 3 kHz is injected into the battery to measure the voltage and current. Then, the phase is obtained. Impedance can be obtained from Equation (1). Until the frequency reaches 0.1 Hz, the next frequency is continuously injected and proceeds in sequence. When the frequency reaches 0.1 Hz, it stops and transmits the impedance value to the PC. Then, a two-dimensional impedance mapping graph is constructed with R and X values.

Figure 4:

Impedance measurement model

3.2 Hardware

Figure 5 presents a block diagram for measuring the impedance of a battery with an EIS module according to the amount of current during charge and the presence of harmonics during discharging. Six lithium-polymer batteries were connected in series to produce 24-V DC. Charging was accomplished with a DC power supply, and the controller was adjusted for both rapid and rated currents. Using the 26-W inverter (24 V, 1 A, 3-phase) we produced a discharge both with and without harmonic wave via the electronic load. The microprocessor (Atmega128P) detected the voltage and charged when the SoC reached 0%, stopping at 100 %. After 50 cycles of charging and discharging, the impedance of the battery was measured using the EIS module.

Figure 5:

System block diagram

Figure 6 shows the experimental device. It comprises a microprocessor, an EIS module, two- and three-level inverters, and a power supply. Table 1 shows the specification of the lithium polymer battery used in the experiment.

Figure 6:

Experimental device

Table 1:

Battery specifications

First, the battery was charged to SoC 100 % , and the initial internal impedance of the battery was measured and discharged using the EIS module. When the SoC was 0 %, charging began until it reached 100%. Then, discharging was repeated, stopping when the temperature of the battery was 50 °C or greater or the battery voltage was 2.5 V or less. For rapid and rated charging experiment, the measures were divided into 1-h (1C) and 30-min (2C) charging sessions. The discharging load measured both with and without harmonics.

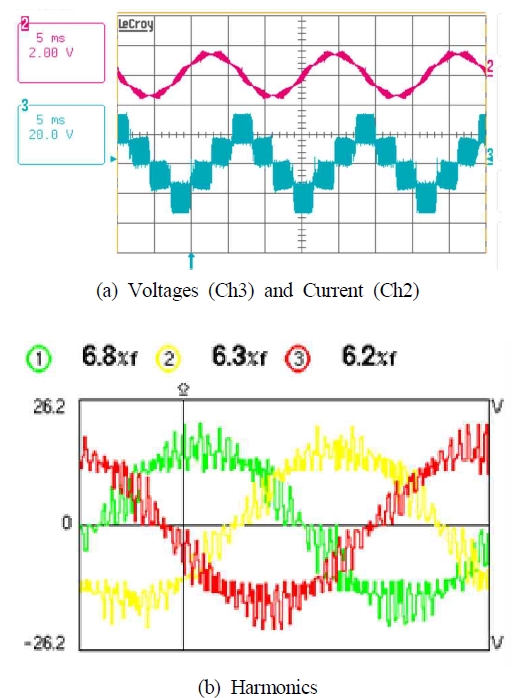
Figure 7 shows the voltage waveform and harmonics components of the 3-ɸ inverter. Figure 7 (a) shows the output voltage and current of the 3-phase inverter, measured with an oscilloscope. Figure 7 (b) shows the harmonics components of the 3-ɸ inverter, measured with a power-quality measuring instrument, resulting in 6.8 %, 6.3 %, and 6.2 %.

Figure 7:

Output voltages and harmonics of the 3-ɸ inverter

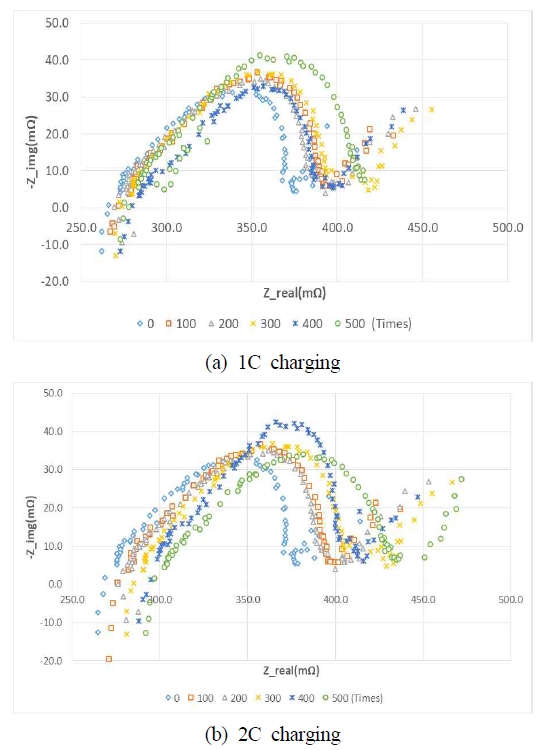
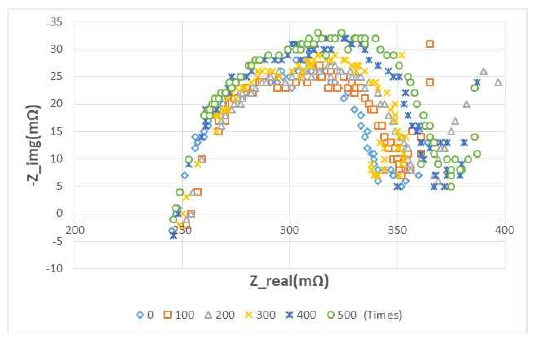
Figure 8 graphs the impedance measurement when harmonics are included. Impedance characteristics were measured through the EIS every 100 charge/discharge cycles at 1C and 2C. Figure 9 graphs the impedance without harmonics. Impedance characteristics were measured with the EIS every 100 charge/discharge cycles. The waveforms are pushed to the right as the number of charge/discharge cycles increase, and Rs gradually increases. Thus, aging is clearly affected by the number of charge/discharge cycles.

Figure 8:

Impedance graph of battery with harmonics discharging

Figure 9:

Impedance graph of battery without harmonics discharging (1C charging only)

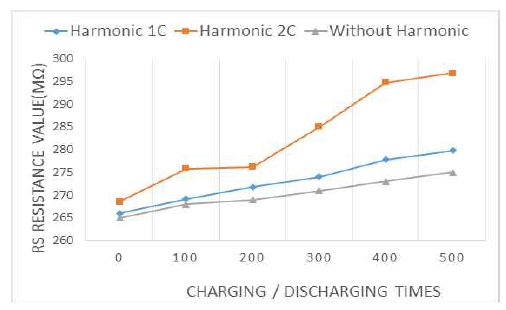
Figure 10 and Table 2 depict lifetime Rs at 1C and 2C. Harmonics are included with 2C, but 1C does not include harmonics. When harmonics were included, the initial value of Rs was 266 mΩ at 1C. However, Rs was measured as 279.8 mΩ after 500 charge/discharge cycles. With 2C, the initial value of Rs was 268.5 mΩ, The Rs value after the initial discharge was 296.8 mΩ. Without harmonics, it increased from 265 mΩ to 275 mΩ.

Figure 10:

Rs with harmonics (1C, 2C) and without harmonics (1C) discharging

Table 2:

Resultant values from Figure 10

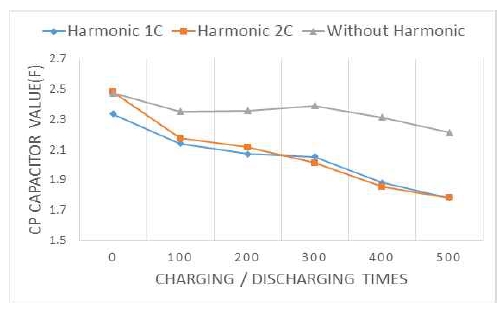
Figure 11 and Table 3 depict the capacity (Rp) at 1C and 2C with one level of harmonics and at 1C without harmonics. The initial values at 1C and 2C with harmonics were 2.335 F and 2.483 F, respectively. After 500 experiments, 1.781 F and 1.783 F were measured. When the harmonics were not included, it decreased from the initial 2.475 F to 2.213 F.

Figure 11:

Rp with harmonics (1C, 2C) and without harmonics (1C) discharging

Table 3:

Resultant values from Figure 11

Author Contributions

The following statements should be used “Conceptualization, T. H. Song and S. G. Lee; Methodology, T. H. Song and H. S. Yang; Software, T. H. Song and H. S. Yang; Validation, T. H. Song and H. S. Yang; Investigation, T. H. Song and H. S. Yang; Resources, T. H. Song and Y. S. Kim; Data Curation, T. H. Song and H. S. Yang; Writing—Original Draft Preparation, T. H. Song; Writing—Review & Editing, T. H. Song and H. S. Yang; Supervision, S. G. Lee; Project Administration, T. H. Song and H. S. Yang; Funding Acquisition, T. H. Song.