해수 유출입 시스템을 적용한 ballast-free 선형의 저항 및 추진 성능에 관한 연구

2.1 지배방정식

본 연구의 수치해석에 적용된 좌표계는 선미에서 선수 방향이 X축의 양의 방향이고 선박의 좌현이 양의 Y축이며, 중력의 반대방향이 양의 Z축으로 하는 직교 좌표계를 이용하였다. 선박의 유동해석을 위해서 지배방정식으로 연속방정식과 3차원 비압축성 Reynolds Averaged Navier-Stokes (RANS) 방정식을 사용하였으며 아래와 같이 표기할 수 있다.

여기서,u_i 는 i 방향 유속, ρ는 밀도, P는 압력, ν는 점성계수를 의미한다. 지배방정식을 풀기위해서 각 유한체적별로 적분을 취하여 인접하고 있는 유한체적 내 그리드 점에서의 물리량들과 상관관계를 구성하여 근사해를 구하는 유한 체적법이 사용하였다.

2.2 수치해석 기법

본 연구에서는 상용 수치해석 프로그램인 Star-CCM+12.06 버전을 이용하였다. 난류 모델은 Realizable k-ϵ 난류 모형을 사용하였으며, k-ϵ 난류 모형은 격자를 선체표면 가까이 분포시킬 필요가 없어서 합리적인 격자수로 계산을 진행할 수 있다. 또한 자유수면을 구현하기 위해 고정된 오일러(Euler) 격자계에서 상간 경계면을 추적하는 방법으로 두 종류 이상의 섞이지 않는 유체의 경계면을 형성할때 주로 사용되는 VOF(Volume of Fraction)법을 사용하였다. 각 상은 하나의 운동량방정식 군으로 지배되고 각 상의 기포율이 해석영역 내에서 격자단위로 계산 된다. 자항 해석을 위해 가상 디스크(Virtual-disc) 모델을 이용한 물체력(Body force propeller) 방법을 사용하였다. 본 방법은 가상의 디스크에 입력조건으로 프로펠러 회전수와 전진비(Advance ratio)에 따른 추력계수(Thrust coefficient)와 토오크 계수(Torque coefficient)를 입력해 줌으로써 전진속도에 맞는 추력(Thrust)과 토오크(Torque)를 내어주는 방법이다.

3.1 대상 선박

대상 선박은 공시선형인 KVLCC2를 사용하였다. 선박의 길이는 320m, 폭은 58m이며 모형선의 축척 비는 160이다. 주요 제원은 Table 1과 같으며 운항 속도는 설계속도인 15.5knots의 속도에서 계산을 수행하였다.

Table 1:

Principal dimensions of ship and model

3.2 격자계 및 경계 조건

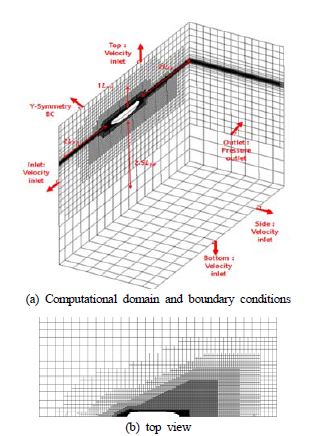
본 연구의 계산에 사용 된 격자 및 경계 조건은 Figure 1과 같으며 계산에 사용된 격자의 수는 Table 2와 같다. 발라스트 트렁크-트림 탱크가 적용되어 격자수가 증가하였으며, 자항 계산 시 가상 디스크 모델의 구현을 위하여 대칭(symmetry) 조건을 사용하지 않았기 때문에 격자수가 두 배로 늘어남을 볼 수 있다. 최소 격자 간격(Y+)는 두 경우 모두 30으로 맞추었다.

Figure 1:

Computational domain, boundary conditions and grid structure

Table 2:

Comparison of the number of cells

3.3 수치 계산 검증

사용된 선형에 대한 수치 계산의 타당성을 검증하기 위하여 인하대학교 선형수조(IUTT, Inha University Towing Tank)에서의 실험 결과와 비교 분석하였으며, Table 3과 같이 정수 중 KVLCC2의 저항, 트림각(trim), 침하량(sinkage)을 비교하였다. 각각 약 2.4%, 18%, 30% 정도의 오차를 가지며, 저항의 경우 큰 차이가 없으나 트림각과 침하량의 경우 작은 절댓값 비교로 인한 높은 오차로 판단된다.

Table 3:

Principal dimension of ship and model

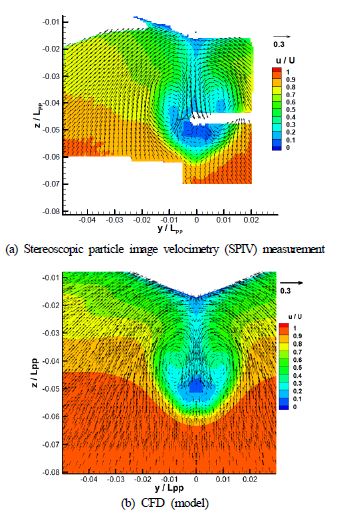
또한 Figure 2와 같이 정수 중 프로펠러 면에서의 공칭 반류를 H. Kim et al. [9]의 실험결과와 비교하였다. 그 속도 분포와 갈고리 모양의 보오텍스(hook shape vortex)가 서로 유사하다고 판단함으로써 CFD 계산의 타당성을 검증하였다.

Figure 2:

Comparison of nominal wake and velocity vector

3.4 해석 조건

본 연구에서는 발라스트 트렁크-트림 탱크의 적용에 따라 유출구 주변의 유동변화가 선체의 성능변화에 영향을 미칠 것으로 판단하여 유출구의 위치와 크기를 변화 시켜가며 해석의 조건을 선정하였다.

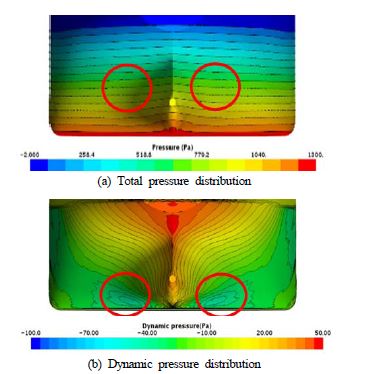
유출구의 위치는 발라스트 트렁크-트림 탱크의 크기를 고려하였으며, Figure 3과 같이 평형수 시스템(Ballast system) 적용하지 않은 선형에서 전체압력이 낮은 부분과 동압력이 낮은 부분을 확인하여 두 가지 유출구의 위치를 선정하였다. 압력이 낮은 부분에 유출구를 적용함으로써 선체의 압력회복이 빨라지는 효과를 기대하였다. 유출구의 크기는 지름 0.03m, 0.015m 두 가지로 선정하였다. 또한 지름이 0.015m인 경우에서 유출구에 유량을 증가시켜 주었을때의 경우를 선정하여 총 네 가지 경우에서 저항 성능 해석을 진행하였다.

Figure 3:

Distribution of total and dynamic pressures

유출구의 위치에 의한 영향을 보기 위해 선미에서 동압력이 가장 낮은 곳을 고려하여 유출구의 위치를 선택하고 지름이 0.03m 인 경우를 Case1, 선미에서 전체 압력이 가장 낮은 곳에 유출구의 위치를 선정하고 지름 0.03m 인 경우를 Case2로 두었다. Case2와 동일한 유출구의 위치에서 지름이 0.015m인 경우를 Case3로 선정하였으며, Case3의 경우에서 유출구에 유량을 증가시켜주어 Case4를 선정하였다. 유량의 결정은 발라스트 트렁크-트림 탱크에 의해 느려진 유출구 유속을 설계 속도와 비슷한 값을 가질 수 있도록 유출유량을 유출구의 크기에 맞추어 0.314kg/s를 선정하였으며, 해당 유량만큼 유출구의 관에서 유체가 분사되도록 하였다.

4.1 저항 성능 해석

본 절에서는 앞서 수행한 수치계산 검증결과가 적절하다는 판단에 의해 각 Case별 저항 성능 해석 결과를 비교해 보았다.

각 Case별 전저항, 마찰저항, 압력저항은 Table 4와 같으며, 유출구를 적용함으로써 저항이 증가함을 확인 할 수 있었다. 또한 마찰저항에서는 큰 차이가 없었으며, 압력저항이 전저항의 차이에 영향을 미치는 것으로 판단된다.

Table 4:

Comparison of total, friction and pressure resistances

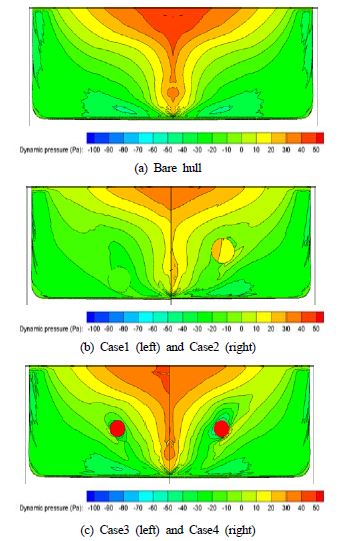
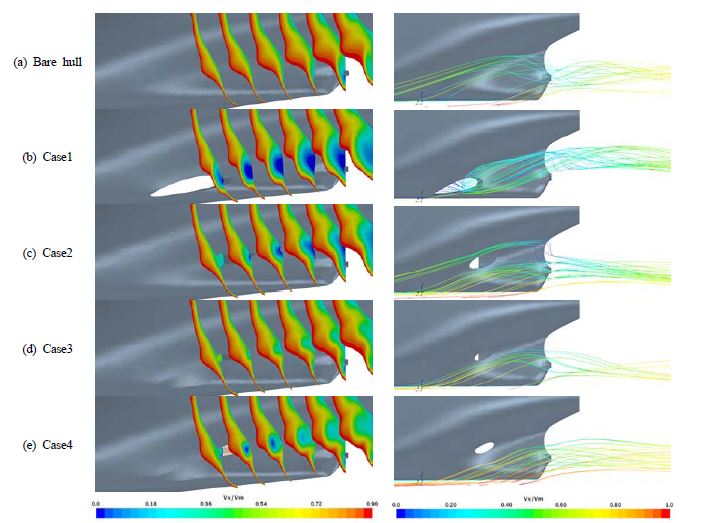
압력의 변화를 확인하기 위하여 Figure 4와 같이 각각의 조건별 압력분포를 비교해 보았으며, 유출구가 존재함으로써 압력의 회복이 bare hull에 비해 더뎌졌다.

Figure 4:

Comparison of pressure distribution

Figure 5:

Comparison of non-dimensional velocity distribution (left) and stream line (right)

동압력이 가장 낮은 곳에 유출구를 선정한 Case1의 경우 보다 전체 압력 중 압력이 가장 낮은 곳에 유출구를 선정한 Case2의 경우가 압력회복 측면에서 유리하였다. 이를 통해 유출구의 위치는 선저보다 상부에 존재할수록 압력회복이 빨라짐을 확인하였다. 또한 직경의 크기를 절반으로 줄인 Case3의 경우 압력회복이 더 빨라졌으며, 유출구의 유량을 증가시켜준 경우 유출구 주변에 압력이 오히려 낮아져 압력회복이 지연되고 있다. 이와 같은 압력회복이 지연되는 원인을 확인하기 위하여 선미부의 무차원화된 속도를 비교해 보았다.

Figure 5의 왼쪽 그림을 통해 무차원화된 속도 분포를 비교할 수 있으며, 압력회복이 느렸던 Case1, 2의 경우 선측에서 유출구에 의한 저속구간이 크게 존재하고 있다. 유출구의 직경을 줄여준 Case3의 경우 bare hull과 가장 유사한 속도분포를 보였다. 압력회복이 느렸던 Case4의 경우 유출구 주변에서 저속구간이 존재하였다.

그 원인으로는 유출된 유체가 선체를 타고 흐르다가 주변의 유속이 느려져 역류하는 것과 같은 현상을 띄고 있을 것이라 분석하였다. 따라서 선체 근처에서는 유속이 빨라져 압력이 낮아지고, 그로 인해 유출구 주변에서의 압력회복이 느려져 앞서 보았던 압력분포를 띄는 것으로 판단된다.

Figure 5의 오른쪽 그림은 프로펠러 면을 지나는 유선을 나타낸 것이다. Case 별로 선미부를 지나는 유선 중 프로펠러 면으로 유입되는 유선들이 다르게 발생하고 있음을 보여준다. Case1의 경우 프로펠러 면으로 유입되는 유선들이 유출되는 유체의 영향을 가장 많이 받고 있으며, 유출구의 위치가 전압력이 가장 높은 곳과 지름이 작아지는 경우 각각 유출구의 영향이 점점 줄어들고 있다. 또한 Case4의 경우 유출구의 영향이 가장 적었으며, 선저를 타고 오르는 유체의 흐름이 프로펠러 면으로 유입되고 있다. 따라서 유출구의 영향이 줄어들수록 선저의 영향이 커짐을 알 수 있다.

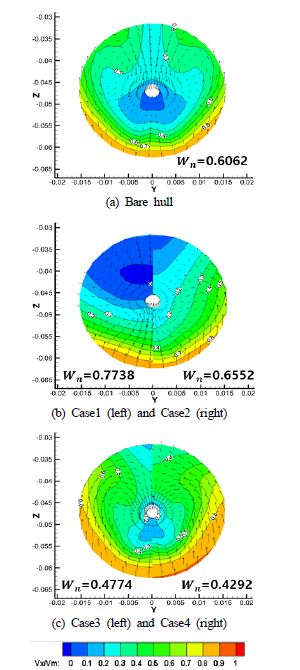
Figure 5을 통해 프로펠러 면으로 유입되는 유선들의 분포를 확인한 결과 Case별 프로펠러 면으로의 유입되는 유속이 다를 것으로 판단되며, Figure 6과 같이 공칭 반류면과 속도 벡터를 비교해 보았다. 그림을 통해 유출구의 직경이 클수록 갈고리 모양의 보오텍스가 적게 관찰되며, 반류면으로 유입되는 유속이 느림을 확인하였다. 유출구의 위치가 선저에서 상부로 올라갈수록 반류면에서의 유속이 빨라짐을 보여준다. 또한 직경이 작아질수록 반류면에서의 유속이 가속되고 있으며, bare hull과 같이 갈고리 모양의 보오텍스가 관찰되어진다. 또한 반류면에서의 유속은 유출구에서 유속을 가속시켜준 Case4의 경우가 가장 빨랐다.

Figure 6:

Comparison of nominal wake and velocity vector distribution

Figure 7:

Position of virtual-disk

4.2 자항 성능 해석

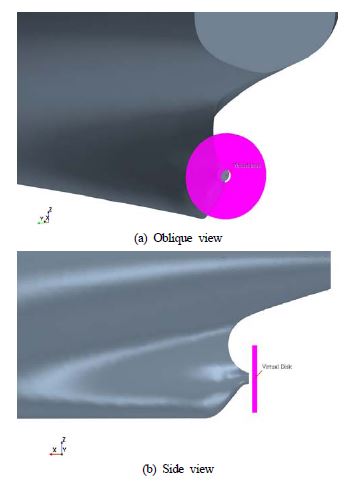
앞 절에서 저항 성능 및 유동분포를 통해 유체성능을 분석해보았다. 본 절에서는 발라스트 트렁크-트림 탱크를 적용함에 있어서 추진 성능의 차이를 보고자 하였다. 추진 성능을 확인하기 위해 자항 해석을 수행하였으며, 자항 해석을 위해 프로펠러를 직접 모델링해주는 대신 프로펠러 위치에 가상의 디스크를 두고 물체력를 통해 전진비에 따른 추력계수를 계산하였다. 입력되는 전진비에 따른 추력계수의 값으로 Natinal Maritime Research Institute(NMRI)에서 실시한 KP458 프로펠러의 POW(Propeller Open Water) 실험값을 사용하였다. 가상의 디스크의 위치는 KVLCC2의 프로펠러의 위치와 동일하며 외경과 내경은 각각 프로펠러와 허브의 직경과 같게 적용하였다. Figure 7에 가상의 디스크를 도시하였다.

물체력의 입력 값으로 유입되는 속도를 정의할 면을 선정해주어야 한다. 유입되는 면은 가상의 디스크에서 X+ 방향으로 직경의 0.1배 떨어진 위치를 선정하였으며 그 크기는 직경의 1.1배 이다.

프로펠러 회전수 변경을 통해 자항점을 찾았으며, 저항 성능이 가장 유리했던 Case4의 경우와 bare hull과의 자항요소를 Table 5와 같이 비교하였다.

Table 5:

Comparison of self-propulsion components

Bare hull과 Case4의 R_TM을 비교한 결과 저항의 증가가 있었으나 그 값이 크지 않으며, ITTC 1957 방법을 이용하여 유효마력(Effective Horse Power, EHP)를 추정한 결과 약 4% 정도 증가하였다.

추진 성능 평가를 위해서 ITTC 1978 추진 성능 해석법을 통하여 자항요소를 추정하였다. η_R 은 물체력을 적용 시 토오크 값을 구하는데 어려움이 있어 토오크의 변화가 없다고 가정하여 1의 값을 사용하였다.

자항해석 결과 프로펠러 면에 들어오는 유속의 증가로인해 η_O가 증가하였다. 하지만 자항상태에서 추력감소계수(Thrust deduction coefficient)의 증가와 반류계수(Wake fraction)값의 감소로 인하여 선체 효율, η_H가 6.5% 감소하였고, 그로 인해 전달마력(Delivered Horse Power, DHP)의 차이가 약 9% 증가하였다. 전달마력 증가의 원인으로 추력감소계수의 증가가 하나의 원인으로 판단되며, 이는 bare hull에 비해 Case4의 경우 자항상태에서 선미부에 영향을 미치는 압력의 변화가 더 클 것으로 판단된다. 또한 프로펠러 회전수가 약 2 RPM 증가했음을 볼 수 있으며, 이는 프로펠러로 들어오는 유속의 증가로 인한 RPM 증가로 보여 진다. 따라서 프로펠러로 유입되는 유속을 고려하여 프로펠러를 재설계함으로써 약간의 추진효율의 증가가 기대된다.

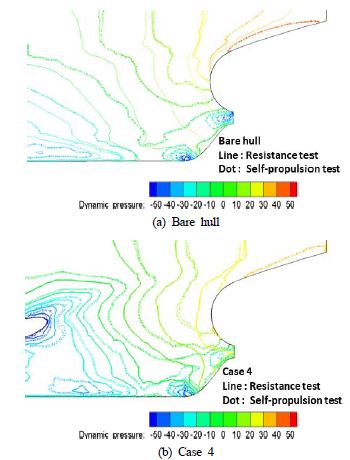
자항상태에서 선미부의 압력분포 차이를 확인하고자 Figure 8과 같이 자항 상태와 저항 상태의 동압력 분포를 비교해 보았다. 그 결과 Figure 8과 같이 자항 상태에서 프로펠러의 회전으로 인해 선미부의 압력이 더 낮아지게 하는 영향을 볼 수 있다. Case4의 경우 저항상태에서 선저부의 빠른 유속으로 인해 선저에서 낮은 압력분포를 보였으며, 자항 상태에서 선저부의 압력이 미치는 영향이 더 큼을 점선과 실선의 비교를 통해서 확인하였다.

Figure 8:

Comparison of dynamic pressure distribution between resistance test and self-propulsion test