선박 좌현 전타 조건에서 프로펠러 편심추력이 추진축계에 미치는 영향 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
일반적으로, 선박 축계는 프로펠러 중량의 영향으로 선미관 후부베어링의 국부적인 지지하중 증가가 현격하게 나타나 잠재적인 축계 베어링 손상의 위험성을 가진다. 이를 방지하기 위한 추진축계 정렬연구는 대부분 준정적 상태(quasi-static condition)에서 프로펠러축과 선미관 후부베어링간의 상대적 경사각을 감소시키는데 중점을 두어 진행되어 왔다. 그러나 보다 완전한 축계 안정성 평가를 위해서는 동적상태에 대한 고려가 필요하다. 본 연구에서는 동적 상태에서 선박 좌현 전타시 과도적으로 변동되는 프로펠러 편심추력이 선미관 내에서 유체 유도 불안정 상태와 스톨(stall)현상을 발생 시키는 것을 확인하였다. 따라서 향후 추진축계 정렬 관련 연구에는 축계 안정성 확보를 위하여 과도상태시 편심추력에 의해 발생하는 불평형 진동 특성을 추가적으로 고려해야 할 필요가 있음을 확인하였다.
Abstract
Normally, a ship’s propeller weight significantly increases the support load of bearings in the ship’s shafting system, which increases the potential risk of bearing failure. To prevent this, a series of studies on shaft alignment are conducted with a focus on reducing the relative inclination angle between the propeller shaft and after stern tube bearing under quasi-static conditions. However, to achieve a more complete stability evaluation of the shafting system, the dynamic state of the shaft alignment must be considered. Our results revealed that propeller eccentric forces, which fluctuate in a hard port turning, demonstrated fluid-induced instability and contributed to stall phenomena in the stern tube. In addition, depending on the specific ship being considered, the opposite results from those in previous studies could be derived. Therefore, the imbalanced vibration characteristics that originate from the propeller eccentric forces in the transient condition must also be considered.
Keywords:
Port rudder turn, Propeller eccentric forces, Fluid induced instability, Imbalanced vibration키워드:
선박 좌현 전타, 프로펠러 편심추력, 유체 유도 불안정, 불평형 진동1. 서 론
축계정렬에 관한 일련의 연구는 1950년대 후반 미국 해군[1]에서 시작되어 1970년대에 걸쳐 다양하게 수행되었다. 특히 1961년, 축계의 안정성을 확보하는데 있어 축계 지지베어링간의 적절한 간격과 높이가 중요한 인자[2]가 됨을 인지하게 되었으며 이를 통해 지지베어링이 추진축의 반력을 적절히 분담받게 함으로써 선박의 무부하 또는 과부하로 인한 축계 지지베어링의 손상이 감소하게 되었다. 일반적으로 베어링이 지지할 수 있는 하중의 허용범위내에서 축계 전체 지지베어링의 개수를 1개 줄일 경우 축계 지지베어링이 받게 되는 반력은 상대적으로 커지지만 선체 변형으로 인한 지지베어링 높낮이(offset) 변화에 따른 반력변화는 상대적으로 작아지므로 축계는 보다 안정적인 상태를 확보할 수 있게 됨은 잘 알려져 있다[3]-[6]. 또한 1990년대부터 선체 외판에 고장력 강판(high tensile strengthsteel)을 점차 확대 적용함에 따라 선체 유연성이 증가되었고 이로써 기존 선박 대비 흘수 변화에 따른 선체 변형량이 커져 지지 베어링의 높낮이 변형 또한 증가하여 축계 베어링 사고로 이어지는 빈도가 높아지는 추세를 보였다. 이에 따라 선체변형을 고려한 축계정렬에 관련된 연구가 활발히 진행되었다[7]-[11]. 그러나, 수행된 연구의 내용을 살펴보면 축계정렬 계산은 주로 준-정적(quasi-static) 조건에서 수행되었음을 알 수 있다. 준-정적 조건이란, 계산은 선박이 정지된 조건에서 수행하되, 동적상태를 간접적으로 고려하기 위하여 선박의 계획 최대 속력으로 운전시 발생하는 프로펠러 편심 추력값을 정적 계산에 굽힘 모멘트 요소로, 열팽창에 따른 베어링 높이 상승분을 추가로 반영하여 계산하는 방식을 말한다. 준정적 조건에서는 계산을 비교적 간략하게 수행할 수 있어 시간과 비용을 저감 할 수 있고, 동적 상태의 축 변형량을 대략적으로 파악하는데 용이한 점이 장점이라 할 수 있지만 실제 동적상태 특히 전타시의 과도조건에서 발생할 수 있는 잠재적인 위험요소를 식별할 수 없다는 데에 한계점이 분명하다. 추진 축계의 동적상태를 고려하는 것은 선급 규칙에 명문화 된 비틀림진동[12]이 대표적인 사례라 할 수 있고, 필요시 선주, 선급에 의해 요구되는 경우 간헐적으로 횡진동 및 종진동에 관한 연구가 수행되고 있다[13]. 문헌검토 결과 동적 상태를 고려한 축계 정렬, 즉 회전축의 거동 연구는 Saitoh에 의해 처음 수행된 것으로 조사되었으며 준정적상태 축계정렬 방식만으로는 운전 시 프로펠러 추력에 기인한 선미관 베어링 및 선미관 밀봉장치 실링(seal ring)의 손상[14]이 나타남을 규명하였다. 나아가 Kuroiwa 등 에 의해 수행된 선박의 선회시 발생하는 프로펠러 편심 추력을 고려한 선미관 베어링의 건전성평가 연구[15]는 단순히 동적 상태뿐만 아니라 선박 전타시 선미부 유동장(wake field)이 급격하게 변동하는 과도상태에서 프로펠러 편심추력의 변화가 추진축계에 미치는 영향 또한 선미관 베어링 건전성 평가에 주요 인자가 됨을 제시하였다. 같은 관점에서 Takahashi 등의 유막 및 축 궤적 분석 연구결과[16] 또한 프로펠러 편심추력이 축계에 미치는 영향을 잘 보여주고 있으며 같은 해 수행된 또 다른 연구[17]도 반류분포에 의한 프로펠러 힘(lateral propeller forces)이 선미관 베어링에 영향을 미치므로 이를 설계 과정에서 고려해야 축계 건전성을 성공적으로 이끌어 낼 수 있다는 점을 보여주었다. 또한 유사한 연구관점에서 S. H. Shin에 의해 선박의 직진, 선회시의 프로펠러 하중이 베어링에 미치는 영향에 관한 연구[18]가 수행된 바 있다. 그러나 아직까지는 선박의 프로펠러 추력이 선미관 베어링에 미치는 영향을 모든 선종에 일괄적으로 적용할 수 없는 한계가 있다. 따라서 선행 연구에서 언급된 바[19]-[21]와 같이 선종별 다수의 사례 분석을 통해 향후 통계적인 분석을 수행할 수 있을 기반을 마련해 나가는 것이 중요하다. 본 연구에서는 한국에서 건조된 4700톤급 선박을 대상으로 선박 좌현 전타시 과도상태의 프로펠러 편심추력이 추진축계에 미치는 영향을 검토하고자 한다.
2. 측정 및 해석 방법
2.1 측정 설비의 구성
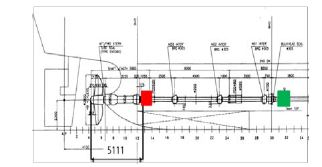
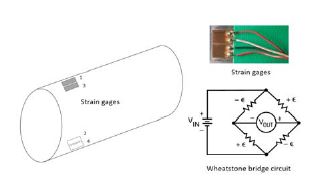
Table 1에서는 연구대상 선박의 축계사양을, Figure 1 및 Table 2에서는 축계 배치도와 스트레인 게이지 및 레이저 Tacho센서 설치위치를 나타내었다.
측정을 위한 텔레메트리 송․수신장치는 Manner 사의 ‘Sensor telemetrie’ 모델로써 Figure 2와 같이 설치하였다. 또한, No.1 중간축에 Compact instrument 사의 Optical Tachometer 센서(A2103/LSR/001)를 Figure 3과 같이 설치하고, 프로펠러 1번 날개 중심선 위치(No.1 cylinder 상사점으로 부터 45° 후방)에 반사테이프를 부착하여 축의 회전속도를 측정 하였다. 최종 설치 계측 시스템 구성은 Figure 4와 같다.
2.2 측정 절차
측정은 Table 3에서와 같은 절차에 따라 수행하였으며, 측정 당시 대상선박의 프로펠러는 물속에 100% 잠긴 상태(100% propeller immersed condition)였으며 선수 / 선미 흘수(draught)는 정지 시 각각 6.3 m / 7.9m, 해상상태는 파고 1.5 m 풍력 17 knot로써 보통수준이었다.
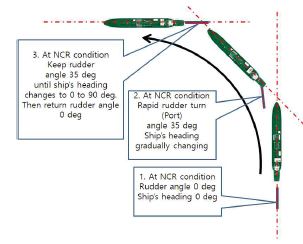
대상선박의 좌현 전타시 발생하는 과도상태를 시험하기 위한 시험조건은 해상인명안전협약(SOLAS)[22] II-1장 제 29규칙 3항 에 따른 주 조타장치 시험요건(최대항해흘수 및 최대 항해속도에서 한쪽 현 35°에서 다른 현 30도°까지 28초 이내)에 준하여 설정하였다. 다만, 본 시험의 목적은 조타장치의 능력(capability)에 관한 사항이 아닌 선박 직진시 대비 전타시 선미의 유동장(wakefield)변화에 의한 과도상태가 선박 추진축계에 미치는 영향을 연구하는 것이 목적이므로 Figure 5에서 와 같이 직진시에서(타각 0°) 한쪽 현 전타(35°)를 수행하고 선박의 항로가 전타 방향으로 90° 변경될 때 까지를 시험조건으로 설정하였다. 또한 선박의 선령, 해상상태, 선박의 감항성을 고려하여 선박의 속도는 NCR 근방으로 제한하였다.
아울러 대상선박의 항적 데이터를 이용 하여 향후 침로에 따른 선박 축계의 상태를 통계적으로 분석하기 위해 Figure 6에서와 같이 GPS 및 전자해도를 통해 선박의 운항 데이터를 수집하였다.
2.3 원신호의 처리[20]
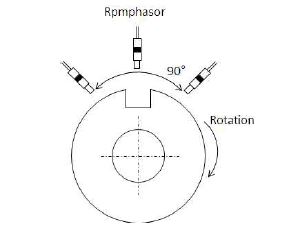
프로펠러 편심추력의 영향을 분석하기 위해서는 시간영역 기반인 원 데이터를 축 중심의 궤적을 나타낼 수 있는 궤도선도(orbit plot)로 나타낼 필요가 있다. 보통 변위신호를 기반으로 하는 경우 Figure 7에서와 같이 계측 위치에 두개의 변위 센서를 축 중심에서 서로 90° 간격을 두고 설치하고 회전속도 검출기를 설치하는 것이 일반적이다.
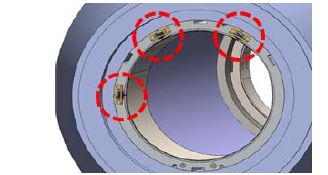
또한 보다 정확한 분석을 위해서는 프로펠러 편심추력에 의한 진폭(amplitude)이 가장 큰 선체 외부의 선미관 후부실(seal) 근방에 비접촉 변위센서를 설치하여 축 중심의 좌표를 구하는 것이 이상적이나[23], 이는 Figure 8에서와 같이 해수에 노출된 위치에 센서를 설치, 고정[24]하기 위해서는 전용의 브라켓(bracket) 제작, 센서 및 안테나 트랜스미터 등의 방수, 방유조치가 부가적으로 수행되어야 하므로 작업의 난이도, 소요시간, 비용대비 효용성 측면에서 현실적인 제약이 있었다.
따라서 이에 대한 대체방법으로 선행 연구[25]에서와 같이 기관실 내에 설치된 스트레인 게이지 정보로부터 계산한 모멘트 성분을 이용하여 궤도선도로 나타낼 수 있는데 이 방법은 전술된 계측법 대비 축의 변위성분은 알 수 없지만 동적상태에서의 축의 거동양상을 비교적 정확히 예측 할 수 있어 실용적이다. 스트레인 게이지로부터 변형률(ϵ)은 게이지가 부착된 위치의 축 단면에서 발생하는 굽힘 모멘트로 환산할 수 있다. 스트레인 게이지의 저항값은 축이 회전하면서 발생하는 수직 변형률(strain)에 비례하여 변동하므로 입력 전압(Vin) 대비 변동된 출력 전압(Vout)을 얻을 수 있으며 이를 통해 Figure 9에서와 같은 풀 휘스톤 브릿지(full wheatstone bridge) 결선방식에서 식 (1)과 같은 변형률 ϵ을 얻을 수 있다.
| (1) |
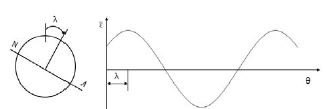
여기에서 Vϵk는 입력전압이며. V0는 출력전압, k는 스트레인 게이지 상수이다. 축 회전에 따른 변형량은 축 회전각도에 따른 값으로 나타낼 수 있으며 Figure 10에서 이러한 회전각에 따른 변형량의 변화 예를 나타내었다.
이러한 사인파형상의 변형량은 굽힘 모멘트, 축의 중립축과 스트레인 게이지 사이의 거리와 밀접한 관련이 있는데 이 관계를 수식으로 표현하면 식 (2)와 같이 나타낼 수 있다.
| (2) |
여기서, ϵa는 변형량 진폭(strain amplitude)을 나타내며, λ는 중립축(N-A; neutral axis)과 수직상태 사이의 각도 즉, 스트레인게이지 설치위치로부터의 각도를 나타낸다. θ 는 수직 방향과 게이지 사이의 각도, ϵ 는 평균변형량(average strain)을 나타낸다. 따라서 축 재료의 종탄성계수 E 와 변형률을 이용하면 축의 굽힘응력 σb를 식 (3)과 같이 구할 수 있다.
| (3) |
여기에서 Mb는 축의 굽힘 모멘트, I는 축의 단면2차 모멘트, C는 축단면의 반지름을 나타낸다.
따라서, 축의 굽힘 모멘트 Mb는 보의 관계식을 적용하여 식 (4)와 같이 구할 수 있다.
| (4) |
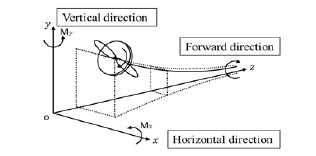
여기서 D0는 축의 외경, Di는 축의 내경, Z는 축의 단면계수를 의미하며, 이를 통해 식 (5) 및 식 (6)과 같이 수직과 수평 모멘트를 계산할 수 있다.
| (5) |
| (6) |
산출된 굽힘 모멘트는 Figure 11과 같이 프로펠러 및 센서 위치의 축 단면에 대해 회전좌표계(a rotating coordinate system)로 도시할 수 있다.
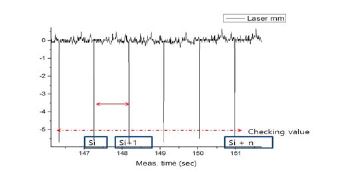
또한 굽힘 모멘트를 궤도선도로 나타내기 위해서는 스트레인 게이지의 신호(원 신호)를 수직 및 수평성분으로 분리 하는 것이 필요하며 파형의 특이점을 보다 용이하게 관찰하기 위하여 시간기반 신호를 축 회전각 기반신호로 변환 하는 작업 또한 필요하다. 시간기반신호(time domain signals)는 Figure 12와 같이 레이저 변위센서로 측정된 tacho신호를 통해 다음 변위신호 수신 시 까지의 시간을 식 (7)에 따라 축 회전수로 변환할 수 있다.
| (7) |
여기서 Si는 변위신호의 i번째 수신시점을 의미한다. 상기와 같은 절차를 통해 시간기반(time domain) 측정치를 회전각 기반(angle domain) 결과로 변환할 수 있다.
3. 결과 및 고찰
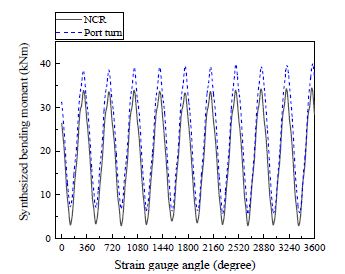
상기와 같은 방법에 의해 도출한 결과는 다음과 같다. 먼저 Figure 13에서는 Table 3의 test#1에 따른 NCR, test#2 및 test#3에 따른 좌현 전타시 계측된 스트레인 게이지 전방향(synthesized) 파형신호를 회전각 기준으로 나타내었다.
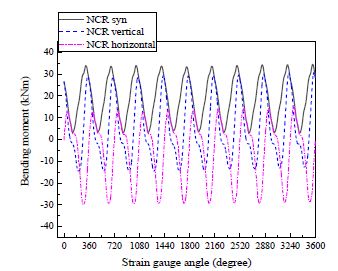
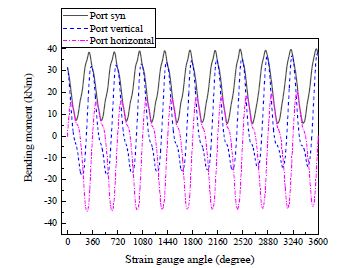
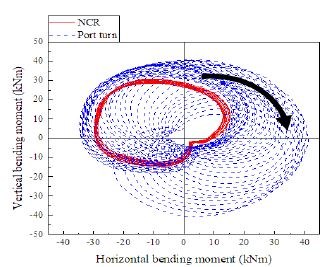
다음으로 Figure 14 및 Figure 15 에서는 상기 두 조건에서의 스트레인 게이지(SG)의 전방향 파형신호를 각각 수직 수평성분으로 분리하여 나타내었으며 좌현 전타시의 과도 상태가 추진축계 거동에 미치는 영향을 비교하기 위하여 Figure 11에 따라 수평성분을 x축, 수직성분을 y축으로 하여 Figure 16에서와 같이 궤도선도(orbit)로 나타내었다.
궤도선도 분석결과 NCR 상태에서는 전형적으로 자유단에서 나타는 원형의 운전형태가 나타남을 확인하였다. 반면, 회전각 기반의 Figure 14 및 Figure 15의 분석결과에서는 NCR 및 좌현 전타시 수평방향 진동 성분이 수직방향 진동성분보다 위상이 약 90° 가량 앞서는 현상이 나타나고 있는데 이는 선미관 내에서 오일 훨(oil whirl) 또는 오일 휩(oil whip)으로 알려진 유체 유도 불안정 상태(fluid-induced instability)의 전형적인 특징으로 판단할 수 있다. 또한 유체 유도 불안정 상태는 Figure 16에서와 같이 orbit이 원형에 가까우며 정방향 세차운동(precession)을 한다는 점이 특징[26]이다. 또한 Figure 16에서는 화살표 방향과 같이 스톨(stall) 징후 발생 전과 발생하는 과정 중의 흥미로운 현상을 보여주고 있다. 스톨(stall)의 원인은 유체의 압력증가, 갑작스런 로터의 증·감속, 등에 따른 유동교란이 원인[26]이므로 선박 직진시 대비 전타시 선미의 유동장의 급격한 변동에 따른 선미관 내의 오일 유동교란이 본 현상의 원인으로 판단된다. 스톨(stall)은 유동교란에 따른 선미부의 압력변화 및 이에 따른 프로펠러 추력의 변화를 가져오며 따라서 선미관 베어링 등 축계 지지베어링의 손상을 초래 할 수 있으므로 본 연구의 결과는 동적상태의 고려가 유의미함을 보여준다고 판단된다. 본 연구선박의 경우 선령과 운항이력을 감안했을 때 예측된 굽힘 응력의 강도와 진폭은 대상선박 축계의 안전성 유지에 영향을 미치지 않는 수준으로 판단된다. 또한 베어링 하중차원에서 고찰은 다음과 같다. 스트레인게이지는 기관실내 선미관 선수 seal에 근접 설치되어 프로펠러와 게이지 사이가 변형이 없는 직선보로 볼 수 있으므로 프로펠러의 운동방항은 스트레인 게이지 위치의 축 거동 방향(시계 하방)과 반대인 반시계 상방으로 이동함에 따라 축을 들어올리는 효과로 선미관 베어링의 국부 하중을 완화시켜 줄 것으로 판단된다. 전술된 연구결과들과 비교할 때 좌현전타 시에는 그 반대의 양상, 즉 축을 베어링 하중방향으로 누르는 경향을 보여 선미관 베어링에 부가 하중을 인가하여 축계 안정성에 부정적인 영향을 미치는 것이 정설로서 받아들여지는 분위기였으나 이번 계측결과를 통해 다른 양상을 보일 수 있음이 확인되었다. 그러나 서론에 기술한 바와 같이 본 연구는 대상선박의 좌현 전타상황에 국한되어 수행되었다. 측정당시의 환경조건, 시간의 제약등에 의해 부분타(좌/우현 10도, 20도) 등에서의 엔진 부하변동 및 선박 진행방향 변화에 따른 영향을 충분히 검토하지 못한 부분, 편심추력의 정량적인 기준이 확립되지 않아 측정결과와의 수치적인 비교가 현 단계에서는 불가한 점은 아쉬움으로 남는다. 또한, 대상선박 뿐 아니라 향후 다양한 선박의 데이터 축적을 통해 프로펠러 편심추력이 추진축계 안정성에 미치는 영향과 그에 따른 실용적 지침 마련은 금후의 과제로 남는다.
4. 결과
본 연구에서는 4,700톤급 선박을 대상으로 좌현 전타 조건에서 프로펠러 편심추력이 축 거동에 미치는 영향을 검토하여 다음과 같은 결과를 얻었다.
- (1) NCR 상태에서는 전형적으로 정상 운전시 자유단에서 나타는 운전형태를 보이고 있음을 알 수 있었으며 전타시의 과도상태가 프로펠러 편심추력 변화를 유발하여 축의 거동에 영향을 미치는 주요 인자임을 확인하였다.
- (2) 좌현 전타시 선미관 내에서 oil whirl 또는 oil whip으로 판단할 수 있는 유체 유도 불안정 상태와 유동이 불안정하게 될 때 나타는 stall현상이 동시적으로 나타나는 것을 확인하였다.
- (3) 좌현 전타시의 프로펠러 편심추력은 NCR 대비 축을 선미관 베어링으로부터 들어 올리는 힘으로 작용하여 선미관 베어링 하중완화에 기여하고 있음을 증명하였다. 또한 선박에 따라서 기존 연구결과와 반대의 양상을 보일 수 있음이 확인되었다.
선박 전타시 변동되는 프로펠러 편심추력은 선미관내 프로펠러축의 유체에 의한 진동 현상을 야기할 수 있다. 이러한 현상이 축 거동에 미치는 영향은 그동안 축계 정렬 시에는 고려되지 않았던 점을 고려하여 향후 연구에는 과도 상태에서 변화하는 편심추력에 의해 유발되는 불평형 진동에 대한 검토가 필요하다.
Acknowledgments
이 논문은 2017년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구(No. 2017R1C1B5017114)이며, 2018 마린엔지니어링 학회 전기학술대회에 발표된 논문을 개선한 것입니다.
References
- M. Rudolph, "A quarter century of propulsion shafting design practice and operating experience in the U.S. navy", The Journal of the American Society of Naval Engineers (NEJ), 71(1), p153-164, (1959).
- W. E. Lehr, and E. L. Parker, “Considerations in the design of marine propulsion shaft systems”, The International Journal of Society of Naval Architects and Marine Engineers (SNAME), 69, p555-601, (1961).
- G. Mann, "Design of propulsion shaft systems using fair curve alignment theory", The American Society of Naval Engineers Journal (NEJ), 76(6), p851-862, (1964).
-
G. Mann, "Analysis of shafting problems using fair curve alignment theory", The American Society of Naval Engineers Journal (NEJ), 77(1), p117-133, (1965).
[https://doi.org/10.1111/j.1559-3584.1965.tb05656.x]

-
G. Mann, "Shipyard alignment of propulsion shafting using fair curve alignment theory", The American Society of Naval Engineers Journal (NEJ), 77(4), p651-659, (1965).
[https://doi.org/10.1111/j.1559-3584.1965.tb04996.x]

- T. A. Wilkin, and W. Strassheim, “Some theoretical and practical aspects of shaft alignment”, IMAS Conference 73 of The Institute of Marine Engineers, 1973. [Online], Available: http://trid.trb.org/view.aspx?id=11182 Accessed March 22, 2016.
- Nippon Kaiji Kyokai (NK), Guidelines on Shafting Alignment, Japan: NK, (2006).
- Wärtsilä, Amendment and Update of the Infromation Provided in Design Group 9709, “Engine Alignment”, Switzerland: Wärtsilä, (2007).
- MAN Dieset & Turbo (MDT), Bearing Load Measurement by Jacking Up, Rev.8. Denmark: MDT, (2012).
- MAN Dieset & Turbo (MDT), Crankshaft Deflection Shop Trial and Sea Trial / Site Trial, Acceptance Criteria, Rev.18. Denmark: MDT, (2014).
-
J. U. Lee, “A study of the analysis of shaft alignment considering hull deflections for 50,000 DWT oil/chemical tankers”, Journal of the Korean Society of Marine Engineering, 40(3), p191-197, (2016), (in Korean).
[https://doi.org/10.5916/jkosme.2016.40.3.191]

- KR, Rules for the Classification of Steel Ships Part 5 Chapter 4 102, Busan, Korea, Korean Register, (2017).
-
J. U. Lee, “Theoretical and experimental analysis of th lateral vibration of shafting system using strain gauges in 50,000-DWT oil/chemical tankers”, Journal of the Korean Society of Marine Engineering, 40(4), p301-306, (2016), (in Korean).
[https://doi.org/10.5916/jkosme.2016.40.4.301]

-
T. Saitoh, "Dynamic alignment taking account of propeller forces and stern tube bearing performances", Journal of the Marine Engineering Society in Japan (MESJ), 18(2), p142-153, (1983).
[https://doi.org/10.5988/jime1966.18.142]

- R. Kuroiwa, A. Oshima, T. Nishioka, T. Tateishi, K. Ohyama, and T. Ishijima, "Reliability improvement of stern tube bearing considering propeller shaft forces during ship turning", Mitshbishi Heavy Industries, Ltd. Technical Review, 44(3), p1-3, (2007).
- S. Takahashi, S. Matsumoto, T. Tateishi, K. Ohyama, R. Kuroiwa, and S. Morohoshi, “Study on oil film analysis of the stern tube bearing under the conditions of dynamic propeller shaft forces”, Transactions of the Japan Society of Mechanical Engineers, Part C, 75(759), p3054-3061, (2009), (in Japanese).
- B. J. Vartdal, T. Gjestland, and T. I. Arvidsen, “Lateral propeller forces and their effects on shaft bearings”, First International Symposium on Marine Propulsors, p475-481, (2009).
- S. H. Shin, “Effects of propeller forces on the propeller shaft bearing during going straight and turning ship”, Journal of the Society of Naval Architects of Korea, 52(1), p61-69, (2015), (in Korean).
-
J. U. Lee, "A study on the analysis of bearing reaction forces and hull deflections affecting shaft alignment using strain gauges for a 50,000 DWT oil/chemical tanker", Journal of the Korean Society of Marine Engineering, 40(4), p288-294, (2016), (in Korean).
[https://doi.org/10.5916/jkosme.2016.40.4.288]

-
J. U. Lee, "Effect of propeller forces into propulsion shafting system in accordance with engine load of 50K DWT class product oil/chemical tanker during ship acceleration", Journal of the Korean Society of Marine Engineering, 41(9), p801-806, (2017), (in Korean).
[https://doi.org/10.5916/jkosme.2017.41.9.801]

-
J. U. Lee, "Effect of engine load dependant propeller eccentric forces on propulsion shaft behavior and the support bearings of 50,000 DWT class oil/chemical tankers in ballast condition", Journal of the Korean Society of Marine Engineering, 42(1), p16-23, (2018).
[https://doi.org/10.5916/jkosme.2018.42.1.16]

- International Maritime Organization (IMO), International Convention for the Safety of Life at Sea (SOLAS), Consolidated ed, London, IMO, (2014).
- B. S. Yang, Condition Monitoring & Diagnostics, Korea: Intervision, (2006), (in Korean).
- American Bureau of Shipping, http://www.sname.org/HigherLogic/System/DownloadDocumentFile.ashx?DocumentFileKey=1a56a8ba-d5b7-4e98-becd-8c09be30ccdd Accessed August 23, 2017.
-
J. U. Lee, “Application of strain gauge method for investigating influence of ship shaft movement by hydrodynamic propeller forces on shaft alignment”, Measurement, 121, p261-275, (2018).
[https://doi.org/10.1016/j.measurement.2018.02.067]

- Incosys, Vibration and Equipment handbook, http://www.incosys.co.kr/index.php/book/book-table?id=945 Accessed March 25, 2017.