정상 동작조건에서 잭업 바지선의 레그에 작용하는 파랑하중 해석

1. 서 론

잭업 바지선(Jack-Up Barge)은 파도나 조류의 영향 없이 육지와 같은 상태에서 작업이 가능토록 지지하는 밑바닥이 평평한 화물 운반선이며 주로 교량 건설, 해상유전개발, 시추작업에 사용된다.

화석연료 사용으로 인한 지구 온난화 문제를 해결하기 위해 세계 각국에서는 기존의 화석연료 사용을 억제하고 비용대비 효율성이 높은 원자력발전의 비중을 확대해 왔지만 일본 후쿠시마 원전 사고를 계기로 여러 국가에서 원자력 발전소 건설을 유보하거나 폐쇄 결정을 내리고 있다. 이를 대체하기 위한 방법으로 다양한 신재생 에너지 개발에 박차를 가하고 있으며 대표적인 신재생 에너지로는 태양광, 풍력 등이 있다. 특히 풍력발전의 경우 유럽 선진국들을 중심으로 육상에 비해 상대적으로 풍자원이 풍부하며 소음문제를 해결할 수 있는 해상에 풍력발전 단지를 조성하는 방안이 주목받고 있다. 국내에서도 최근 정부의 신재생에너지 개발계획에 따라 서남해안 해상풍력 실증화 단지개발을 위한 프로젝트로 해상풍력단지가 설치되고 있다.

해상 풍력 발전기의 설치는 고 중량의 상부구조물을 안정적으로 설치하기 위해 잭업 시스템을 갖춘 해상 풍력 발전기 설치선을 필요로 한다. 설치선이 작업을 수행할 때 대부분의 환경외력은 잭업 레그에 작용하기 때문에 안정적인 작업수행을 위해 다양한 환경조건하에서 잭업 레그의 안전성 확보가 필수적이다. 잭업 레그에 대한 해양 동역학적 수치해석 연구는 파랑 중 비선형 운동 응답의 관점에서 많은 연구가 진행되고 있다[1]-[3].

J. Seok et al. [4]은 해상 운반에 관한 연구로 플로팅 독(dock)을 이용한 방파제용 케이슨의 운반 및 설치에 대한 안정성 검토를 수행하였다. C. H. Jo et al. [5]은 해양환경 조건에 따른 동적운동, 와이어장력 그리고 훅 로드 등의 검토를 통한 해상 운반 안정성 검토를 수행하였다. D. C. Hong et al. [6]은 선형 포텐셜 이론을 이용하여 바지선의 손상침수 시 자세변화가 미치는 운동 특성 변화에 관한 연구를 수행하였다. B. W. Nam et al. [7]은 예인 시 발생 할 수 있는 안정성 문제에 대한 연구로 실험과 수치해석 방법을 통해 운송 바지선의 예인 안정성 검토를 하였다. S. H. Heo et al. [8]은 잭업 바지선의 동적 응답 해석에 대한 연구를 수행하였다. J. Seok et al. [9]은 상용 포텐셜 코드인 MAXSURF를 활용하여 바지선의 안정성을 평가하였다.

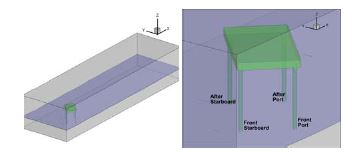
본 논문에서는 전산유체역학(CFD)을 이용하여 정상 동작조건에서 잭업 바지선을 지지하는 레그(leg)에 작용하는 힘을 계산하는 것과 이 힘을 사용하여 구조해석용 파랑하중을 산정하는 방법을 제시하였다. 대상구조물은 Figure 1에 보여준 서남해안 근해에 설치될 잭업 바지선이다.

상용 CFD 코드인 STAR-CCM+를 이용하여 레그에 작용하는 힘을 계산하였다. 외력은 유속, 파도 그리고 바람으로 정의하였다. 외력의 방향은 Heading, Quartering 그리고 Beam Loading 3가지이다. 외력의 방향에 따라 레그 별로 힘을 분석하였다. 레그 별로 작용하는 최고 힘과 레그 간의 간섭 효과의 유무를 확인하였다. 구조해석을 위해 레그 길이 별로 단위길이 당 작용하는 힘의 분포, 대표 힘 그리고 힘의 중심점 산정 방법을 제시하였다.

Figure 1:

Jack up barge employed for analysis

2. 대상구조물 및 해석조건

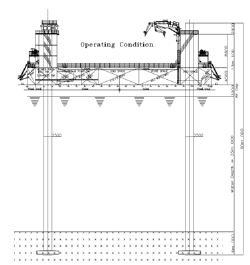
해상에서의 각종 토목공사 작업지원을 위한 잭업 바지선은 스포팅 레그(Surporting Leg)의 구조강도 평가를 위해 파랑하중 해석이 필요하다. 본 연구에서는 파랑하중 해석을 위해 전산유체역학(CFD, Computational Fluid Dynamics) 시뮬레이션을 수행하였다. 대상구조물의 흘수조건은 Figure 2에 나타낸 대로 정상 동작조건(Normal Operating Condition) 이다.

Figure 2:

Leg drawing of Jack up barge

Figure 2의 구조물 치수, 설치될 해상상태와 해석조건을 Table 1에 나타내었다. 스포팅 레그(Surporting Leg)의 깊이(H)는 35m, 파고(h)는 1.5m, 파의 주기(s)는 8초, 파장(λ)은 118.16m, 유속(Current Velocity)은 1.5m/s, 풍속(Wind Velocity)은 36m/s, 에어 갭(Air Gap)은 3.0m 그리고 레그의 지름(Leg Diameter)은 2.5m이다. 그리고 외력인 유속, 파도 그리고 바람의 방향은 Heading, Quartering 그리고 Beam 3방향 이다. 본 논문에서는 모형 크기(Model Scale)에서 계산을 한 후 푸르드 스케일링(Froude Scaling)에 의한 실선 크기(Full Scale)로 확장하는 방법을 사용하였다. 모형크기의 축척비는 20을 사용하였다.

Table 1:

Particulars for normal operating condition

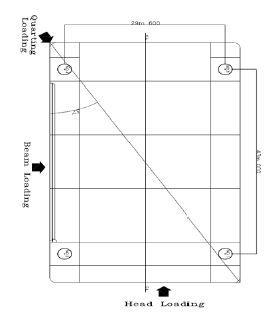
Figure 3는 잭업 바지선의 상판 형상과 외력인 유속, 파도 그리고 바람의 방향을 나타낸 것이다. 앞서 언급한 대로 외력은 방향은 Heading, Quartering 그리고 Beam 3방향으로 하였다.

Figure 3:

Deck drawing of Jack up barge

3. CFD 해석

3.2 격자시스템

일관된 파를 전파시켜 스포팅 레그에 도달시키기 위해서는 파 조건에 맞는 격자를 구성해야 한다. 본 해석에서는 길이방향 격자크기와 높이방향 격자크기의 비(Aspect Ratio)를4이하가 되도록 하였다. 격자는 약 300만개를 사용하였으며 y+는 70 이하를 유지하였다.

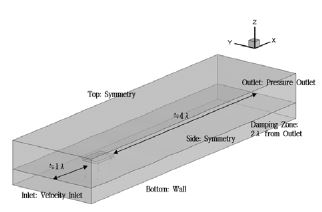
본 연구에서 고려된 좌표계, 해석영역 및 경계조건은 Figure 4에 나타내었다. 여기서 λ는 본 해석에 고려된 파장이다. 경계조건의 경우 입구영역에 velocity inlet을, 출구영역에 pressure outlet 조건을 부여하였다. 바닥부에는 wall 조건을 부여하여 점착조건을 만족시키도록 하였다. 나머지 모든 경계에서는 symmetry 조건을 부여하여 경계에 의한 속도 구배가 없도록 하였다. 그리고 파에 대한 반사파를 최소화시키기 위해 출구영역 부근에 damping zone을 설정하였다. 본 해석에서 사용된 파형 모델(Wave Model)은 Table 1에서 정의된 H/λ의 값이 wave breaking limit인 0.142를 넘어서기 때문에 비선형성이 강한 wave breaking 현상이 나올것으로 판단하여 fifth order stokes wave를 고려하였다. 자유표면은 VOF(volume of fluid) 기법으로 처리하였다.

Figure 4:

Coordinate and numerical domain

4. 결과 분석

4.1 Current, Wave & Wind 방향에 따른 Leg 명칭

4.1.1 Heading & Beam Loading

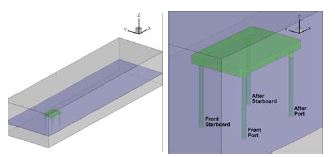
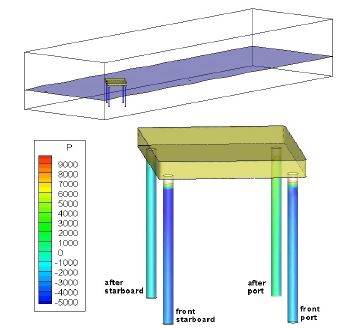
Figure 5는 Heading loading에서의 레그 위치 별 명칭이다. Figure 4와 같이 보면 외력이 유입되어 처음으로 만나는 레그를 앞쪽 좌현(Front Port)과 앞쪽 우현(Front Starboard)으로 정의하였고, 뒤쪽에 위치한 레그를 뒤쪽 좌현(After Port)과 뒤쪽 우현(After Starboard)으로 하였다. Beam loading은 아래 Figure 5의 상태에서 구조물을 90도 회전하여 해석하였다. 따라서 회전 후의 레그 위치 별 명칭은 Heading loading과 동일하다.

Figure 5:

Leg definition at the heading loading

4.1.2 Quartering Loading

Figure 6은 quartering loading에서의 레그 위치 별 명칭이다.

Figure 6:

Leg definition at the quartering loading

4.2 레그 주위 유동 및 압력분포

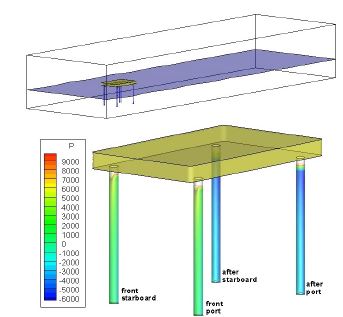
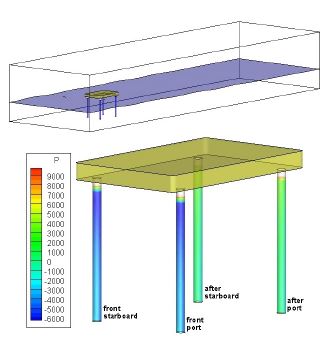
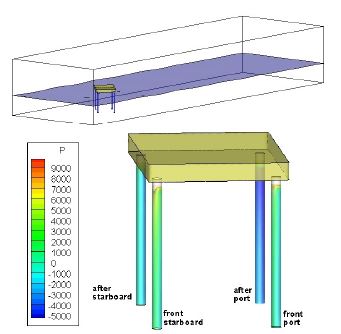
레그에 작용하는 압력은 식 (3)의 첫째항인 정압(static pressure), 두 번째 항인 정수압(hydrostatic pressure) 그리고 세 번째 항인 동압(dynamic pressure)의 합으로 표현된다. 본절의 압력분포는 실선 크기로 확장한 결과이며 식 (3)에서 정수압을 제외한 정압과 동압만을 나타낸 것이다. 4.3절과 4.4절에서는 식 (3)의 압력을 바탕으로 모든 조건들에서 레그 별로 힘을 나타내었다. 이 때 힘은 식 (3)의 모든 압력 즉, 정압, 정수압 그리고 동압을 고려한 것이다.

$\[ P_T\left(pa\right)=P_S+pgz+\frac{1}{2}\rho V^2 \]$

(3)

Figure 7은 외력이 Heading으로 작용할 때 4개 레그 압력의 합이 가장 클 때의 유동과 압력분포를 나타낸 것이다. 앞쪽 좌현과 앞쪽 우현에서는 큰 양(+)의 압력이 그리고 뒤쪽 좌현과 뒤쪽 우현에서는 큰 음(-)의 압력이 각각 동일하게 나타났다.

Figure 7:

Pressure distribution at the heading loading(maximum pressure)

Figure 8은 외력이 Heading으로 작용할 때 4개 레그 압력의 합이 가장 작을 때의 유동과 압력분포를 나타낸 것이다. Figure 7과 반대로 앞쪽 좌현과 앞쪽 우현에서는 큰 음의 압력이 그리고 뒤쪽 좌현과 뒤쪽 우현에서는 큰 양의 압력이 각각 동일하게 나타났다.

Figure 8:

Pressure distribution at the heading loading(minimum pressure)

Figure 9는 외력이 quartering으로 작용할 때 4개 레그 압력의 합이 가장 클 때의 유동과 압력분포를 나타낸 것이다. 앞쪽 좌현과 앞쪽 우현에서는 큰 양의 압력이 그리고 뒤쪽 좌현과 뒤쪽 우현에서는 큰 음의 압력이 각각 동일하게 나타났다.

Figure 9:

Pressure distribution at the quartering loading(maximum pressure)

Figure 10은 외력이 quartering으로 작용할 때 4개 레그 압력의 합이 가장 작을 때의 유동과 압력분포를 나타낸 것이다. 앞쪽 좌현과 앞쪽 우현에서는 큰 음의 압력이 그리고 뒤쪽 좌현과 뒤쪽 우현에서는 큰 양의 압력이 각각 동일하게 나타났다.

Figure 10:

Pressure distribution at the quartering loading(minimum pressure)

4.3 시간변화에 따라 레그에 작용하는 힘

본 절에서는 외력의 방향에 따라 각 레그에 작용하는 힘을 시간변화에 따라 나타내었다. 힘은 식 (3)을 바탕으로 식 (4)로 정의하였다.

$\[ Force\left(N\right)=P_T\left(pa\right)\times Area\left(m^2\right) \]$

(4)

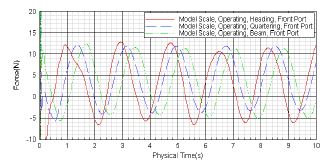
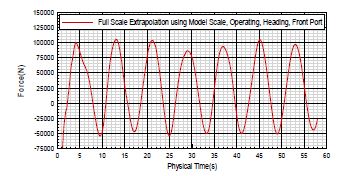
Figure 11은 외력 별로 앞쪽 좌현의 레그에 작용하는 힘이다. 계산영역에서 외력이 들어오는 위치가 동일하기 때문에 외력의 방향에 따라 힘의 위상이 달라지는 현상을 보여주었다. 시간에 따라 레그에 작용하는 최고 힘을 보면 heading 때에는 9초, quartering 때에는 14초, Beam 때에는 17초에서 약 12N이 작용하는 것을 알 수 있으며 일정한 주기를 가지는 것을 확인하였다.

Figure 11:

Force acting on the front port according to loadingdirection (model scale)

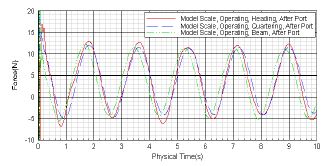
Figure 12는 외력 별로 앞쪽 좌현의 레그에 작용하는 힘이다. 앞쪽 좌현의 결과인 Figure 11과의 차이점은 힘의 위상이 거의 동일한 것이다. 최고 값 관점에서의 힘의 크기는 앞쪽 좌현의 결과와 거의 동일하다.

Figure 12:

Force acting on the after port according to loading direction (model scale)

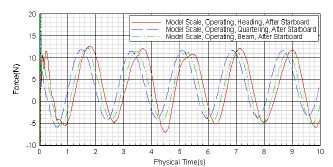
Figure 13은 외력 별로 앞쪽 좌현의 레그에 작용하는 힘이다. 뒤쪽 좌현의 결과인 Figure 12와 비교해 보면 Heading과 Beam Loading은 거의 동일한 결과를 보여주고 있다. Quartering의 경우 위상의 차이를 보여주고 있다. 그러나 최고 값 관점에서는 거의 동일한 결과를 보여주었다.

Figure 13:

Force acting on the after starboard according to loading direction (model scale)

Figure 11 ~ Figure 13의 결과를 보면 레그 위치 별로 힘의 최고 값, 최저 값 그리고 주기 측면에서 거의 동일한 결과를 보여주었으며 이는 레그 서로 간의 간섭 효과는 거의 없다는 것을 설명해 주고 있다.

Table 2는 외력의 방향에 따라 레그에 작용하는 최고 힘을 나타낸 것이다. 6초에서 10초 사이 힘 중에서 최고 힘을 선정하였다. 레그 별로 약 11.2(N)에서 12.0(N) 범위 내에서 최고 힘이 작용하였다.

Table 2:

Maximum force acting on the legs according to loading direction(model scale)

2장에서 언급한 대로 실선 크기에서의 힘을 알기 위해서 모형 크기로 계산한 결과를 식 (5)에 따라 확장 하였다. λ는 축척비로 20을 사용하였다. Figure 14는 실선 크기에서의 값이다.

$\[ Force \left(Full Scale\right) = Force \left(Model Scale\right) \times {\lambda }^3 \]$

(5)

외력의 방향에 따라 시간 별로 힘은 거의 동일하고 위상만 차이를 보여주었기 때문에 Heading Loading 시 앞쪽 좌현에 대한 결과만을 Figure 14에 나타내었다.

4.4 구조해석을 위한 레그 길이 별 단위길이 당

작용하는 힘 분포

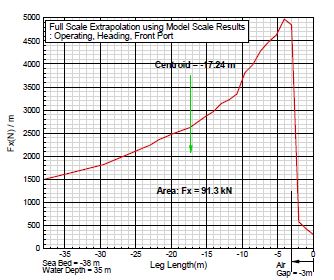
본 해석의 주 목적인 레그 길이 별로 단위길이 당 작용하는 힘의 분포, 대표 힘과 힘의 중심점 산정이 필요하다. 여기서 단위길이 당 분포된 힘은 유동과 동일방향으로 작용하는 힘 즉, F_X(Figure 4 좌표계 참조)이다. Figure 11 ~ Figure 13의 결과를 보면 레그 별로 작용하는 힘에는 다소 차이를 보였으나, 수치해석 상의 오차범위로 판단된다. 따라서 구조해석을 위한 실선 데이터는 Figure 14의 앞쪽 좌현에 작용하는 힘을 사용하는 것이 적절할 것으로 판단된다.

Figure 14:

Full scale extrapolation by model scale

Figure 15의 가로축은 레그 길이를 나타내고 세로축은 단위길이 당 작용하는 힘을 나타낸 것이다. 가로축의 0의 위치는 잭업 바지선의 하판을 나타낸 것이고, –3m는 정지 자유수면의 위치이다. 자유수면 근처에서 단위길이 당 작용하는 힘이 가장 큼을 알 수 있고 수심이 깊어질수록 감소됨을 확인 하였다.

레그에 작용하는 대표 힘과 중심점 계산은 다음과 같다. 대표 힘은 곡선에 둘러싸인 전체 면적이고, 중심점은 그 영역의 도심이 된다. 본 구조물의 작업환경에서 대표 힘은 91.3 kN이 산정되었고 중심점은 잭업 바지선의 하판으로부터 17.24m에 위치하였다.

Figure 15:

Force acting on legs per unit length, total force and center point of force

4. 결 론

본 논문에서는 전산유체역학을 바탕으로 정상 동작조건에서 잭업 바지선의 레그에 작용하는 힘을 산정하고 이 힘을 사용하여 구조해석을 위한 파랑하중을 계산하는 방법을 제시하였다.

• 1) 외력은 해류, 파도 그리고 바람으로 정의하였고 외력의 방향은 Heading, Quartering 그리고 Beam Loading에서 해석을 수행하였다. 외력의 방향에 따라 힘의 위상이 달라지는 현상을 보았다. 힘의 크기는 최고 값만 고려해 보면 대동소이한 결과를 보여 주었다. 그리고 레그서로 간의 간섭효과는 거의 나타나지 않은 것을 확인하였다.
• 2) 구조해석을 위한 파랑하중 정보는 레그 길이 별로 단위 길이 당 작용하는 힘의 분포, 대표 힘과 힘의 중심점 산정이 필요하다. 단위길이 당 분포된 힘은 유동과 동일방향으로 작용하는 힘임을 알아야 한다.
• 3) 본 결과는 추후 잭업 바지선의 레그 설계에 유용한 자료로 활용 가능하다고 판단된다.

References

• X. Y. Zheng, and C. Y. Liaw, “Non-linear frequencydomain analysis of jack-up platforms”, International Journal of Non-Linear Mechanics, 39(9), p1519-1534, (2004). [https://doi.org/10.1016/j.ijnonlinmec.2004.02.013]
• M. J. Cassidy, Non-Linear Analysis of Jack-Up Structures Subjected to Random Waves, Ph.D. Thesis, Department of Civil Engineering, University of Oxford, UK, (1999).
• M. S. Williams, R. S. Thompson, and G. T. Houlsby, “Non-linear dynamic analysis of offshore jack-up units”, Computers & structures, 69(2), p171-180, (1998). [https://doi.org/10.1016/s0045-7949(98)00119-9]
• J. Seok, J. C. Park, J. K. Heo, H. Y. Kang, Y. H. Bae, M. H. Kim, and Y. K. Kang, “Stability evaluation during transportation of caisson for breakwater”, Journal of Ocean Engineering and Technology, 24(4), p13-22, (2010), (in Korean).
• C. H. Jo, S. J. Kim, and H. Cheong, “Dynamic stability during transportation of bridge caisson”, Journal of Ocean Engineering and Technology, 23(1), p104-108, (2009), (in Korean).
• D. C. Hong, and S. Y. Hong, “Waveload analysis for heeled barges with flooded compartments”, Journal of Society of Naval Architects of Korea, 42(4), p379-287, (2005), (in Korean).
• B. W. Nam, S. Y. Hong, J. H. Kim, S. K. Choi, and J. W. Kim, “Experimental and numerical study on towing stability of transportation barge”, Journal of Ocean Engineering and Technology, 28(2), p102-110, (2014), (in Korean). [https://doi.org/10.5574/ksoe.2014.28.2.102]
• S. H. Heo, W. C. Koo, and M. S. Park, “Dynamic response analysis of a jack-up leg with pile-soil interaction”, New & Renewable Energy, 12(1), p10-18, (2016), (in Korean). [https://doi.org/10.7849/ksnre.2016.03.12.1.10]
• J. Seok, Y. S. Back, J. C. Park, S. Y. Kim, T. H. Cha, and Y. J. Yang, “Stability evaluation during transportation of offshore wind turbine by barge”, Journal of the Society of Naval Architects of Korea, 54(3), p196-203, (2017), (in Korean). [https://doi.org/10.3744/snak.2017.54.3.196]