Design and performance evaluation of a 10W pico-hydro portable turbine using computational analysis
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The fast-developing world requires significant amounts of energy while conventional fossil fuel is gradually being depleted. Hydropower increasingly proves its potential not only as an environmentally friendly source of energy, but also one that is affordable to supply a considerable part of the world’s energy demand. This research focuses on the development of a 10W pico-hydro portable turbine, which can be used not only for leisure activities, but also for emergency life safety systems. The rotor blade is designed based on the blade element momentum theory by employing a modification of NREL S815 airfoil. Accordingly, the turbine was analyzed with the computational fluid dynamics approach with an appropriate setup model. The power coefficient of the turbine peaked at 0.37 at a rated tip speed ratio of 2 when it was used without casing. The flow pattern and wake formation behind the turbine were taken into consideration. A comparison of the extracted power under different incoming velocity conditions was also conducted and presented in this paper.
Keywords:
Pico-hydro turbine, CFD analysis, Renewable energy, Performance evaluation1. Introduction
In our modern world, renewable energy performs an increasingly essential function in economy as well as in industry. It is calculated that in 2016, renewable energy accounted for 2006 GW of electricity production. Globally, hydropower is the leading source of electricity generation among these renewable energy sources. At 1122 GW, it supplies 56% of all renewable electricity, which can supply electricity to a billion people. Moreover, of the new renewable capacities installed globally, 58% are in Asia [1]. There remains vast untapped potentials around the world, especially in developing countries. However, the pace in hydropower development is not the same around the world. The most potential areas for exploiting hydropower are in East Asia and North America with estimated supply amounts of 1190 and 703 TWh, respectively. Experts predict that by 2050, the worldwide capacity can be doubled [2].
Hydro energy is typically extracted by a number of methods, such as water wheels, hydro turbines, or hydro-electric plants with a variety of power scales from a few kilowatts to hundreds of megawatts. Scientists and researchers expend substantial efforts in this field in order to develop more equipment with higher efficiencies. D. Powell et al. [3] developed a pico-hydro turbine generator system, which is capable of generating approximately 100 W of power; it supplies electricity to a compact electrochemical cell for off-grid water disinfection. Meanwhile, a water wheel turbine, suitable for sites with fast and shallow surface flows, such as rivers or tidal currents, was developed by M. H. Nguyen et al. [4]. They concluded that a water wheel turbine, with six or nine blades, effectively operates at small tip speed ratios. K. Gaiser et al. [5] applied a response surface methodology and experiment to evaluate the effect of jet angle, blade number, nozzle diameter, and rotational speed at revolutions per minute (RPM) on the efficiency of a pico-hydro turgo turbine.
Most studies concentrate on affordable turbines to supply power at household or village scales. Accordingly, a small-scale hydro turbine suitable for leisure activities, lighting LED bulbs, and charging mobile phones, tablets, or any small electrical devices, is conceptualized. It is anticipated to be useful during travel or picnics in remote areas without any source of electricity. In this study, a pico-scale 10W hydro turbine is designed and investigated. This type of turbine is capable of working in shallow water regions, such as rivers, streams, and canals with flow speeds ranging 1 ~ 1.5 m/s. The pico-hydro turbine should satisfy critical requirements: it should be lightweight and sufficiently small to be portable and can operate under different working conditions. The turbine blade is firstly designed based on the blade element momentum theory (BEMT) and then modeled to create a three-dimensional (3D) full geometry. Numerical simulations of the three-blade hydro turbine are conducted under a series of working conditions in order to evaluate the generated power and efficiency of the turbine.
2. Methodology of Turbine Design
2.1 Blade design and turbine specifications
Blade shape is one of the most essential factors, which significantly affects turbine performance. The blade has to satisfy not only the high lift-drag ratio and high cavitation performance criteria, but it must also be easy to manufacture and possess sufficient strength to operate under various working conditions. Therefore, the blade airfoil selection has an important function in the entire design process. Based on the aforementioned requirements, a modification of S815 hydrofoil in the NREL thick foil family [6] is selected with the primary aim of improving the lift-to-drag characteristic (Figure 1). The foil thickness is reduced to 60% to achieve better dynamic characteristics, reduce the weight of the entire turbine, and ensure blade strength. In order to facilitate its fabrication, the trailing edge of the airfoil is adjusted to become rounder. Besides, the sharp edge at the end of the foil may lead to low quality mesh and therefore reduce the calculation accuracy.
By decreasing the hydrofoil thickness, the maximum lift-drag ratio improves significantly. A Reynolds number of 100 000 accounted for 33.6 (at α = 5.5o) for foil modification compared with 18.4 (at α = 17o) for the original foil. The variation in the lift coefficient and lift-drag ratio versus the angle of attack are displayed in the Figure 2.
2.2 Blade design
The blade geometry is designed using our laboratory software, which is programmed based on the blade element momentum theory and other additional calculations. The BEMT, which is used for analyzing the hydrodynamic performance of wind or tidal turbines, is employed in the design process of the turbine blade. The general BEMT is based on the combination of momentum and blade element theories. The momentum theory is used to derive the axial and tangential flow reduction factors with inclusions of tip loss factors to consider the finite number of rotor blades. The blade element theory is used to model the blade section drag and torque by dividing the rotor blade into a number of elements [7]. Figure 3 shows the components of velocity and force distribution in a blade element.
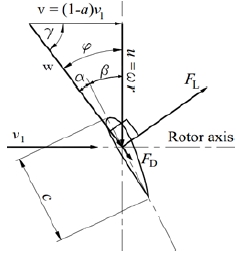
Velocities and forces acting on a blade element (source: Blade Element Theory, W. Froude, D. W. Taylor, S. Drzewiecki)
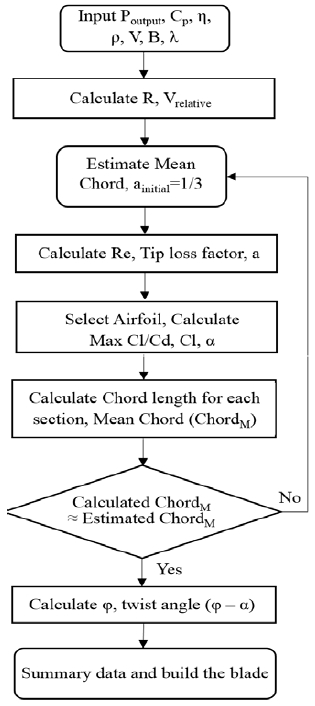
The repeated calculation of blade parameters is illustrated in Figure 4, where the output power, expected coefficient, mechanical efficiency, number of blades, and incoming water velocity are inputted as initial key factors. The blade diameter and tip speed ratio are determined by Equation (1) and Equation (2), respectively, as follows:
| (1) |
| (2) |
| (3) |
where D is the blade diameter, P is the output power, Cp is the expected efficiency, η is the mechanical efficiency, λ is the tip speed ratio, ν1 is the flow velocity, Vrel is the relative velocity, ω is the angular velocity, ChordM is the blade mean chord, and ν is the kinematic viscosity.
In the first loop, the blade mean chord is estimated and utilized to calculate Reynolds number. Then, the hydrofoil dynamics characteristics at that Reynolds number are analyzed at several attack angles (α) using XFLR5 software to determine the value of α where Cl/Cd ratio is maximum. Using the initial value, a = 1/3, the tip loss factor is calculated for all blade sections by Equation (4). Thereafter the axial induction factor, -a, is recalculated Equation (5).
| (4) |
| (5) |
| (6) |
| (7) |
where R is the blade radius, r is the radius at a certain position, C is the chord length, B is the number of blades, f is the tip loss coefficient, a is the axial reduction factor, and Cl is the lift coefficient.
Equation (6) determines the chord length of each blade section based on the lift coefficient (Cl), tip loss factor (f), and recalculated axial reduction factor (a). Hence, the mean chord of the whole blade is calculated and compared to the initially assumed mean chord. This loop repeats several times until two values of the mean chord (estimated and calculated) are close to each other. At the end of the process, the twist angle for each section is specified as the difference between angles φ and α.
In this study, the airfoil covers 70% of the blade length, from r/R = 0.3 to r/R = 1. The blade is divided into 15 different sections; however, only the parameters for the eight main sections are shown below. Several calculations yielded geometry data for blade design, including twist angle and chord length for each blade section, from root to tip as listed in Table 1. Meanwhile, the tip loss coefficient is calculated and illustrated in Figure 5.
Table 2 summarizes the designed parameters of the 10W pico-hydro turbine. The turbine is designed to operate at a rated velocity of 1.2 m/s. From the calculations, the outer and hub diameters of 0.21 and 0.074 m, respectively, were obtained. Based on the results of another research conducted in our laboratory, the number of blades was three. The three-blade turbine exhibits its best performance at various incoming water flows and a number of rotational speeds. After the design parameters are obtained through several calculations, the Solidworks software is employed to model the 3D geometry of the turbine.
2.3 Casing design
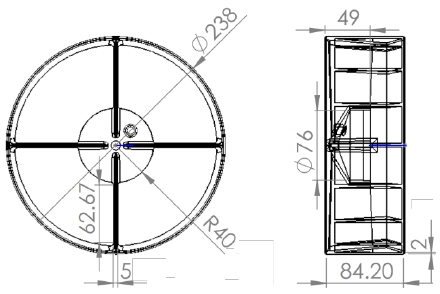
The casing, which is an indispensable component of the turbine apparatus, not only functions as a frame to protect the blade from damage caused by external forces. It also contains a small generator, which converts the turbine rotation to electricity and stores it inside an enclosed battery. Because the turbine is portable and can work flexibly underwater, the turbine blade cannot operate on its own; a front casing is required. The casing functions as an installation space as well as an intermediate component between the blade and connecting rod. The casing design must satisfy some of the following requirements: adequate strength to protect the blade from external impact; sufficient space for the blade and generator to fit; simple construction to reduce flow velocity reduction. Based on the aforementioned criteria, and considering the axial distance (between the casing frame and blade) and tip clearance (distance between blade tip and inner wall casing), the casing was built using the detailed parameters shown in Figure 6. The casing consisted of four supports with a 238 mm outer diameter, an 84.2 mm total casing width, and a 76 mm room for installing the generator. The front edges that are directly in contact with the flow are rounded in order to reduce flow resistance. The full three-dimensional model of the turbines (with and without casing) are displayed in Figure 7.
3. Numerical Method
3.1 CFD approach and turbulence model
In this study, the CFD simulation method is employed to analyze the performance of the pico-hydro turbine under different operating conditions. In the simulation analyses, the turbine performance was tested at a TSR range of 0.5 - 4 with a 0.5 step. Three incoming water velocities were applied: 1, 1.2, and 1.5 m/s. The turbine efficiency is evaluated by a power coefficient, which is calculated from the torque on the blade given by Equation (8).
| (8) |
where T is the torque on the blade and A is the sweep area.
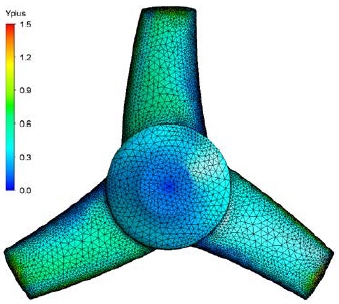
The turbulence model is an essential factor; it indicates the accuracy of numerical simulations. The shear stress transport (SST) turbulence model is one that is preeminently built based on the k–ω model in the near wall region, but utilized in the k–ε formulation on the far field. It is designed to provide highly accurate initial predictions of the onset and amount of flow separation under adverse pressure gradients through the inclusion of transport effects into the eddy-viscosity formulation. This results in a major improvement in terms of flow separation predictions. Because of these improvements, it is commonly used in modeling wind and hydro turbines, as utilized in this study. In his research, M. Rahimian concluded that the simulation results that employed the SST turbulence model agreed better with the experimental results than those of other models [8]. The blade region is controlled by a y-plus value (Y+) of approximately 1 in order to ensure the accuracy of the near wall treatment at low Reynolds number computations provided by the SST turbulence model. The current numerical computation is performed with multiple frames of reference approach; the flow field and casing domains are in a stationary frame while the turbine blade domain is in a rotating frame.
3.2 Mesh formation and grid sensitivity
The hybrid mesh is created independently for three fluid domains, including the flow field, rotor blade, and casing domains, using the commercial software Ansys-Workbench. The unstructured mesh is used by dint of the casing complexity and the leading and trailing edges in the rotor domain, whereas the flow field domain employs a structured mesh based on hexa-hedra type elements. A local refinement of the mesh is applied at some important regions, such as the leading and trailing edges of turbine blades, in order to capture the flow field structure precisely. The distribution of the y-plus value on the blade can be observed in Figure 8. The number of elements in each domain is carefully determined after conducting a mesh-independent study. To validate the accuracy of numerical computations, it is essential to conduct a mesh sensitivity study of computational domains. As for the theoretical aspect, the finer the mesh, the fewer grid-related errors occur [9]. Thereafter, the power coefficient at a rated TSR and the designed flow velocity are considered as standard parameters to evaluate five grids and determine the impact of mesh size on solution accuracy. The same turbulence model (the SST) is used to compare the power coefficient of each case.
The mesh-independent study is conducted in five cases with different grid sizes from rough to fine meshes and extremely fine mesh. The number of elements for each grid and the influence of mesh on power coefficient are demonstrated in Figure 9. It can be clearly seen that the turbine obtained a higher power coefficient when a finer mesh was applied. However, the discrepancy among the power coefficients of the grid with 7.4, 8.9, and 9.5 million elements was negligible. Therefore, to ensure the balance between the simulation accuracy, computer resource, and time consumption, a grid with 7.4 million elements was considered as the most suitable to achieve precise simulations.
3.3 Boundary conditions
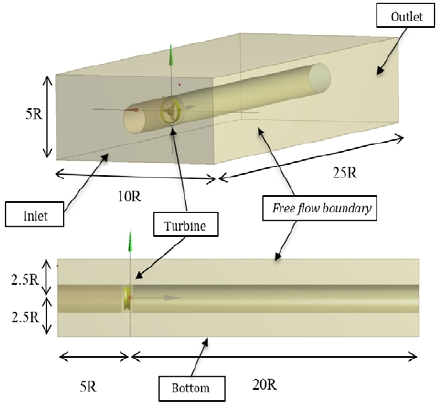
Figure 10 illustrates the flow field domain dimension, turbine installation position, and boundaries. In terms of the flow field, the domain size is 5R × 10R × 25R (where R is the blade radius), which is sufficiently large to capture the flow pattern and wake behind the turbine. The inlet boundary is set at a normal speed. A static pressure is imposed at the field domain outlet. The top and side faces are of the free flow boundary type where water can freely enter or exit the domain, whereas the casing and turbine blade are set up as a free slip wall boundary. In this numerical simulation, multiple frames of reference are involved. The rotor domain is in a rotational frame, whereas the two remaining domains are in stationary frames. The interfaces between rotational and stationary components are set as a frozen-rotor type, and those between two stationary domains are set as general connections. All simulations were performed in a steady state analysis and reached a convergence criterion of 1×10−5 for accuracy.
4. Results And Discussion
4.1 Flow pattern
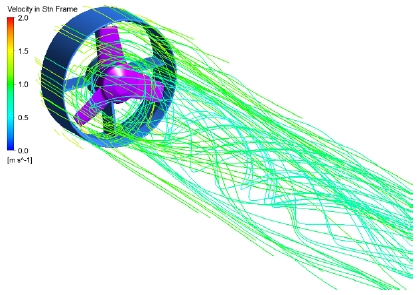
Figure 11 illustrates the wake pattern after water passed through the turbine when it worked at TSR 2 and an incoming velocity of 1.2 m/s. By dint of operating under a designed condition, the turbine experienced a good behavior. The streamline appeared smooth without any abnormality in its flow pattern. It is reasonable according to the basic characteristics of fluid particles that passed through the turbine rotor. In the case of installing a casing to work with the turbine blade, the generated wake was more complex considering that more vortices were formed than when the turbine was bare.
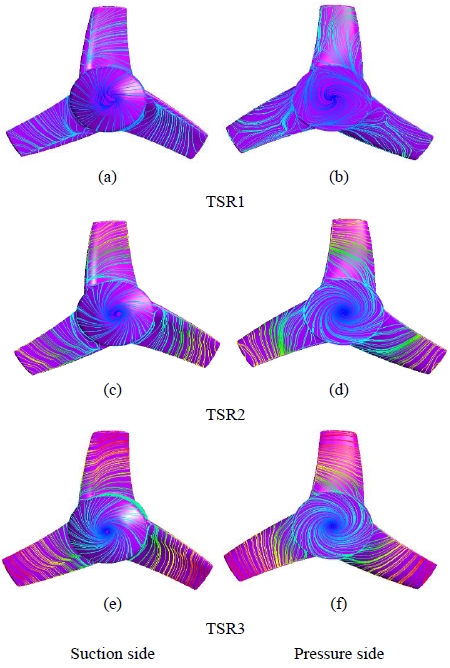
Detailed streamlines on the blade surface are shown in Figure 12; the streamlines on the blade surface were distributed more evenly and reasonably by the increase of TSR (from TSR 1 to 3). In these computational analyses, the TSR values were changed by keeping the flow velocity constant and varying the rotational speed. At TSR 1, because of the low rotational speed, there were radial flows on the suction surface where water particles tended to move in a direction away from the root to the tip of the blade. This type of flow does not contribute to the energy transfer process between water and turbine. This phenomenon explained why the turbine extracted less energy when working at a low TSR value. At a higher rotational speed (for TSRs 2 and 3), the fluid within the turbine’s wake region flowed following the turbine’s rotational movement. The streamlines were smoother without disturbance and the radial flow ceased. It indicated that most of the water particles that passed through the turbine forced the blade to rotate and generate power.
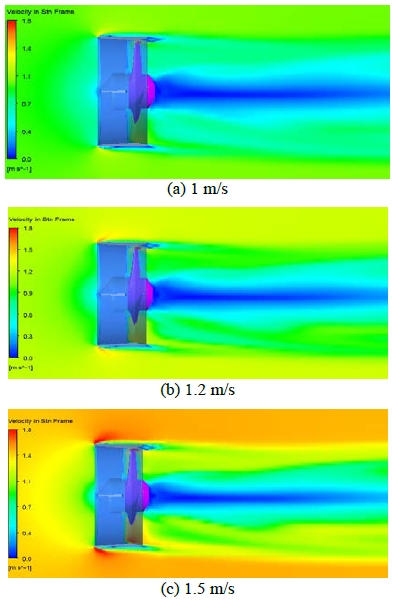
Figure 13 plots the velocity field around the blade and casing. The flow velocity variation ranged from 1 to 1.5 m/s. It can be observed that when the water flow came into contact with the casing and blade, some areas with high speed motion (such as in the casing edges and blade tips) were generated. This occurred because of the combination of flow velocity and rotor blade rotation; it made the velocity at the blade tip increase significantly and caused a well-known phenomenon - a blade tip vortex. It was observed that at a high inflow velocity, the low speed area behind the turbine was narrow. The torque on the blade was achieved from simulations; hence, the extracted power was calculated at different TSR values and flow velocities; results are compared and presented in the following section.
4.2 Turbine power and efficiency
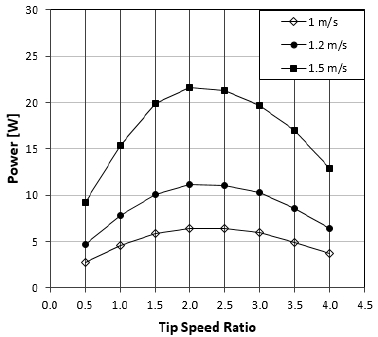
Figure 14 shows the output of this turbine at three water velocities: 1, 1.2, and 1.5 m/s. Evidently, higher flow velocities resulted in higher generated power. Under all circumstances, the maximum power output was obtained when the turbine rotated at a rated speed of TSR 2 followed by TSR 2.5, with a small reduction in the absorbed power. At a lower TSR (under 1) and a higher TSR (above 3), the turbine degenerated. This was indicated by the lower amount of energy obtained from water. In the case of the 1.5 m/s flow velocity, the power was considerably higher compared with those of the two remaining conditions. However, at a velocity of 1.2 m/s, the turbine was also capable of generating an amount of electricity, which satisfied the design requirement. The simulation results exhibited a good agreement with the estimated power calculated by a formula in which power is directly proportional to the cube of velocity.
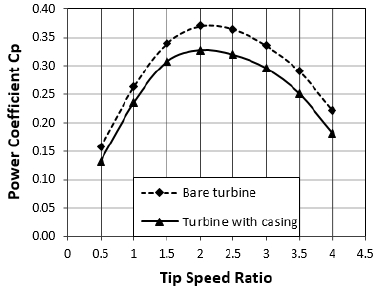
As for the turbine efficiency, Figure 15 shows the turbine power coefficient when working with and without casing. In general, under both operating conditions, according to the increase in the TSR, the turbine efficiency increased gradually. It achieved the highest value at the rated TSR before it decreased and thereafter increased to another higher value. Without the casing, the turbine performed best at TSR 2 and peaked at a Cp of 0.37. The presence of the casing resulted in a Cp reduction for the whole range of the surveyed rotational speed. As demonstrated by the 2.5% decrease in turbine efficiency, at a low TSR, the casing effect on turbine performance was low. On the other hand, when the TSR values were either rated or higher, the power coefficient was significantly influenced and accounted for 4.5% of the decrease. In others words, with the same flow velocity but at a higher rotational speed, the casing makes it more difficult for the turbine to obtain energy from water. Nevertheless, the casing was essential to protect the turbine blade from external forces as well as to house a small generator that converted the rotational movement into electricity.
A series of hydro turbine efficiency curves produced by several researchers are plotted in Figure 16. Although each turbine had its own peak at a different TSR value, the efficiency curve patterns were the same. Among these, Coiro's turbine [10] had the best performance with a maximum Cp of 0.39, followed by the work reported by Bahaj [11]. The studies of Bryden [12] and Kinnas [13] had similar maximum power coefficients. On the other hand, the 10W pico-hydro turbine introduced in this study only had a Cp of 0.33 (indicated by the red line) in Figure 14. The results of previous studies provided valuable information and were a useful reference to validate the current study. The 10W pico-hydro portable turbine should be tested with a real model in experiments to confirm the reliability of the CFD results. This will be the next step in our research.
5. Conclusions
The 10W pico-hydro turbine was designed based on the BEMT, and the hydrodynamic characteristics were evaluated using the CDF approach. To summarize the aforementioned work, some of the conclusions drawn are as follows:
- (1) Turbine characteristics satisfied the design requirements, including the generation of sufficient power at a rated point. The turbine was light and sufficiently small to be portable.
- (2) In terms of performance, when equipped with a casing, the turbine achieved a maximum power coefficient of 0.33 at a rated TSR = 2, which corresponded to a rotational speed of 220 RPM. Depending on the rotor speed, employing a casing effected a 2 ~ 4.5% reduction in the power coefficient.
- (3) When the water flow velocity was changed, there was no remarkable disparity among the observed turbine efficiencies; however, the turbine power output was significantly influenced. The output increased to 80% when the water velocity was increased from 1.2 to 1.5 m/s.
- (4) Although the pico-hydro turbine only had an average efficiency, it could be useful for leisure activities, especially in remote areas. It can be used for lighting bulbs and charging devices. The turbine has a high potential to be used for life safety systems and emergency situations. Consequently, marine structures will probably be equipped with the proposed turbine in the future.
Acknowledgments
This work (No. C0442118) was supported by Business for Cooperative R&D between Industry, Academy, and Research Institute funded Korea Small and Medium Business Administration in 2016
References
- International Renewable Energy Agency, Renewable capacity highlights, International Renewable Energy Agency (IRENA), United Arab Emirates, (2017).
- Team at IHA central office, Hydropower Status Report, International Hydropower Association, United Kingdom, (2015).
-
D. Powell, A. Ebrahimi, S. Nourbakhsh, M. Meshkahaldini, and A. M. Bilton, “Design of pico-hydro turbine generator systems for self-powered electrochemical water disinfection devices”, Renewable Energy, 123, p590-602, (2018).
[https://doi.org/10.1016/j.renene.2017.12.079]

-
M. H. Nguyen, H. C. Jeong, and C. J. Yang, “A study on flow fields and performance of water wheel turbine using experimental and numerical analyses”, Science China Technological Sciences, 61(3), p464-474, (2018).
[https://doi.org/10.1007/s11431-017-9146-9]

- K. Gaiserac, P. Ericksona, P. Stroeveb, and J. Delplanque, “An experimental investigation of design parameters for pico-hydro Turgo turbines using a response surface methodology”, Renewable Energy, 85, p406-418, (2016).
-
J. L. Tangler, and D. M. Somers, NREL Airfoil Families for HAWTs, Colorado, US, National Technical Information Service, (1995).
[https://doi.org/10.2172/10106095]

- W. M. J. Batten, A. S. Bahaj, A. F. Molland, and J. R. Chaplin, “The prediction of Hydrodynamic performance of marine current turbines”, Renew Energy, 33(10), p85-96, (2006).
-
M. Rahimian, J. Walker, and I. Penesis, “Numerical assessment of a horizontal axis marine current turbine performance”, International Journal of Marine Energy, 20, p151-164, (2017).
[https://doi.org/10.1016/j.ijome.2017.07.009]

- J. H. Ferziger, and M. Peric, Computational Methods for Fluid Dynamics, Berlin, Germany, Springer, (1996).
- J. Baltazar, and J. A. C. Campos, “Unsteady analysis of a horizontal axis marine current turbine in yawed inflow conditions with a panel method”, Proceedings of the International Symposium on Marine Propulsors, p1-9, (2009).
- D. P. Coiro, U. Maisto, F. Scherillo, and F. Grasso, “Horizontal axis tidal current turbine: numerical and experimental investigations”, Proceeding of Offshore Wind and Other Marine Renewable Energies in Mediterranean and European Seas, p1-7, (2006).
- S. A. Kinnas, and W. Xu, “Performance prediction and design of marine current turbines”, Proceedings of the Society of Naval Architects& Marine Engineers, p1-10, (2010).
-
I. G. Bryden, S. Naik, P. Fraenkel, and C. R. Bullen, “Matching tidal current plants to local flow conditions”, Energy, 23(9), p699-709, (1998).
[https://doi.org/10.1016/s0360-5442(98)00021-8]