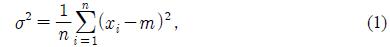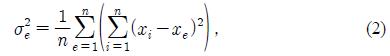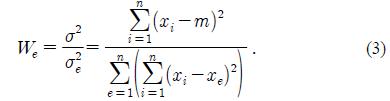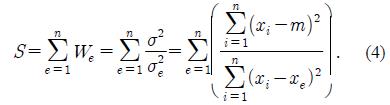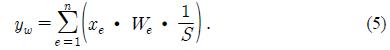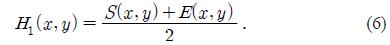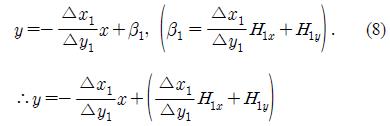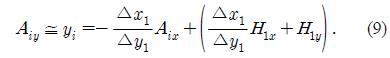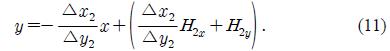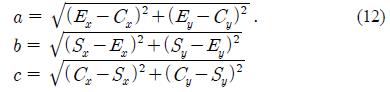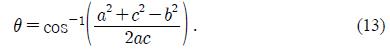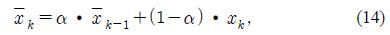Relative azimuth estimation algorithm using rotational displacement

1. Introduction

Real time location systems(RTLSs) using a wireless communication technology, which provides useful information to users by recognizing the position of objects, have been widely applied in various areas such as medical, logistical, and industrial areas [1]-[6]. Recently, an indoor navigation system based on a RTLS has been introduced that can guide a user to a desired destination in a complicated indoor environment when the global positioning system (GPS) is not available [7]-[9]. If this system provides azimuth information as well as location information to users, they can easily be aware of their location and a specific direction to proceed to without any problem. Basically, these systems are required to provide precise position and azimuth information; thus, they must be robust to radio transmission irregularities and minimize the estimation error that occurs from sensor noise and magnetic disturbances. Therefore, several azimuth acquisition methods have been studied because the azimuth information is essential for indoor navigation systems.

Lee et al. [10] proposed an indoor tracking model that employs a digital magnetic compass(DMC) to determine the orientation of a target in real-time and an accuracy refinement algorithm that removes noise in RSSI signals before they are used for distance and location estimation. Another approach involves the use of a filter, which can efficiently reduce the drift error of inertial sensors, and produces a possible solution without magnetic sensor has been proposed[11]. However, in order to achieve higher tracking accuracy, a magnetic sensor is necessary. Thus, Zhang et al. [12] presented a method to appropriately solve and handle the magnetic sensor data that adds a function for detecting and minimizing the magnetic field disturbance to the complementary separate-bias Kalman filter. More recently, they proposed a method that utilizes acceleration, angular rate, and magnetic field sensors to provide a long-term stable orientation solution by suggesting the use of a modified Kalman filter [13]. However, the error accumulates with time because the system is calculated recursively. Many of these systems use a wireless sensor network with several sensors for localization data acquisition plus a specific algorithm with a filter for additional error compensation owing to sensor drift. Because this magnetic sensor is sensitive to electromagnetic noise attributed to a variety of electronic devices, power lines, etc. that can deteriorate its accuracy, it is difficult to obtain satisfactory output azimuth information. To solve this problem, the acquisition of azimuth information that is robust and stable against electromagnetic interference is required for the indoor navigation system.

This paper presents a novel algorithm for relative azimuth estimation by considering the rotational displacement of a mobile node without any magnetic sensors that are affected by electromagnetic noise in an indoor space. The proposed algorithm based on an environment in which a mobile node draws circular arcs with arbitrary radius predicts the central point via the starting and ending points of the arc on the basis of the coordinate data of the mobile node obtained by the fixed nodes. In addition, the proposed algorithm estimates the relative azimuth by acquiring the rotation angle from these three points. In addition, we propose an improved weight average filter in order to effectively reduce errors in the rotational displacement and then obtain a stable accumulated average error even after several repetitions with time.

2. Proposed relative azimuth algorithm

2.1 Preprocessing using an improved weight average filter

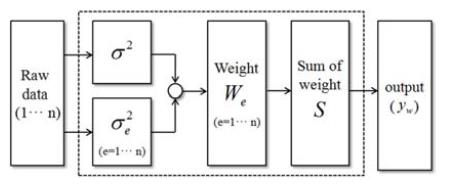
Preprocessing, which effectively remove noise in the raw data acquired from nodes with inherent errors, is very important because it affects the accuracy of the relative azimuth. Generally, raw data acquired from the localization based on wireless communication includes noise due to clock drift and offset and especially propagation loss or distortion caused by obstacles in the non line of sight (NLOS) environment. A large number of methods used to reduce noise during preprocessing include a standard median filter, weighted median filter, center-weight median (CWM) filter, adaptive center weighted median (ACWM) filter, and modified adaptive center weighted median (MACWM) filter [14]-[16]. Although these filters use a threshold based on variance that provides reasonable noise removal performance to their systems, it is difficult to select the appropriate threshold value in the NLOS environment because the size of the impulse is changed in real-time. Therefore, this paper presents an improved weight average filter (IWAF) to improve these problems during preprocessing that can effectively remove impulse noise by applying each different weighting value, depending on the size of each impulse noise without threshold from the position data acquired from a mobile node and then calculating the average value. First, the IWAF is applied to reduce impulse noise in the acquired position data of mobile nodes following the procedure in Figure 1.

Figure 1:

Block diagram of improved weight average filter

Generally, the population variance(σ²) is expressed as

where n is the number of raw data points, x_i is the i-th raw data point, and m is the average of the raw data points. The modified variation that represents the variation based on e-th raw data point is given by

where x_e represents the value of e-th raw data point, and the maximum value of σ²_e is limitless but a positive real number. As σ²_e becomes bigger, the standard deviation based on e-th raw data point becomes larger, and the noise characteristics of x_e appear strongly. This noise characteristic has the range of variation 0 to 1 and a weight given by

The size of W_e is expressed as a value between 0 and 1. The closer the value of W_e is to 0, the stronger its noise characteristic is. The closer the value of W_e is to 1, the weaker its noise characteristic is. The total sum(S) of W_e that gives each different weight to each raw data point is

Accordingly, to apply the different weights depending on the size of the noise to the raw data, the average (y_w) is

In Equation (5), y_w reduces the impulse noise, which is relatively large compared to the other noise source, because a larger impulse noise implies the use of a smaller weighting value.

2.2 Estimation of relative azimuth

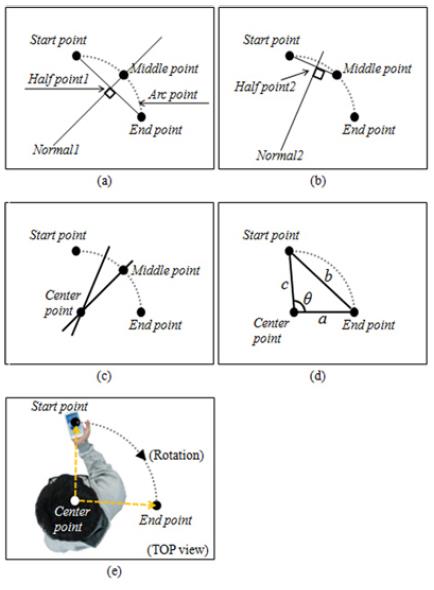
The relative azimuth estimation method of the proposed algorithm is described as the stages (a)-(d) in Figure 2. When a user rotates a mobile node, as in Figure 2 (e), the node acquires an arbitrary arc point A_i(x,y), where i is the index number of the acquired arc point. S(x,y) is the starting point, E(x,y) is the ending point, H₁(x,y) is a point halfway between S(x,y) and E(x,y), which is expressed as

Figure 2:

Sequence of proposed relative azimuth estimation

The equation of a straight line passing through S(x,y) and E(x,y) is

where α_n is y-intercept. The normal equation (y) passing through H₁(x,y) is

M(x,y) is the middle point that is the closest arc point A_i(x,y) from the normal. M(x,y) resulting from the substitution of A_ix into Equation (8) is selected as the following Figure 3 and Equation (9).

Figure 3:

Acquisition of middle point (M(x,y))

H₂(x,y) is another point halfway between S(x,y) and M(x,y) using the same method in Equation (6). The equation of a straight line passing through S(x,y) and M(x,y) is

The normal equation (y) passing through H₂(x,y) is

C(x,y) is the center point obtained by Equation (8) and Equation (11), where C(x,y) is the center axis when a user rotates a mobile node. At the stage in Figure 2 (d), each side of the triangle with three points consisting of S(x,y), E(x,y), and C(x,y), are determined as follows

Furthermore, the interior angle(θ) between a and c is calculated by the second law of cosines.

Because θ is the revolved angle of mobile node by user, the direction of a user can be estimated from the relative azimuth by summing the previous azimuth with θ.

3. Simulation result and analysis

3.1 Analysis of proposed IWAF

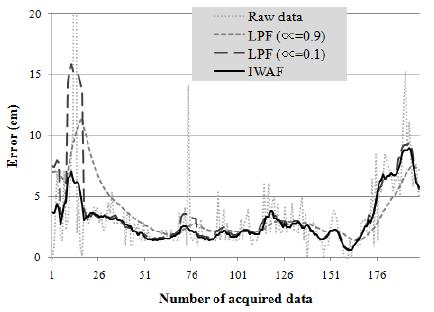
Simulations were carried out in order to verify the performance of the proposed algorithm. Figure 4 shows the performance of other filters compared to the proposed IWAF with a standard weight filter generally expressed as

Figure 4:

Performance of proposed weight average filter.

Where x_k is the present weight average, α is a weight that has a value between 0 and 1, x_k-1 is the previous weight average, and x_k is a present average. When the x-axis value is about 10 in Figure 4, the raw data represents a form of an impulse, and as α changes, the characteristic of WF is also changes. Here, when α is large, a droop phenomenon occurs even if impulse is reduced because of the dependence on the previous raw data. This droop phenomenon is not suitable for preprocessing because it affects the impulse for a long time. On the other hand, the advantages of the proposed IWAF are that the droop phenomenon does not exist because the weight is not assigned according to the time, and the impulse noise decreases faster than the general weight filter because the weight is assigned depending on the size of impulse noise. Therefore, the IWAF is suitable for preprocessing to improve the performance of the proposed algorithm and can be applied widely in the field of signal processing using image, control, and sensor processing in which impulse noise exists.

3.2 Analysis of proposed relative azimuth estimation algorithm

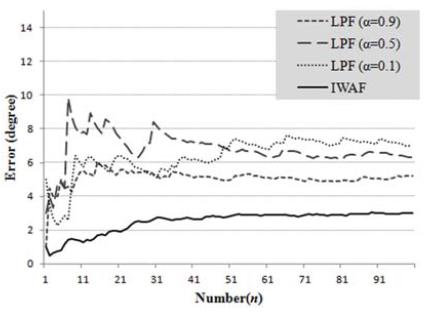
Computer simulations are performed to evaluate the performance of the proposed relative azimuth estimation algorithm. The components and conditions for the simulation environment are the angular velocity (90 rad/s), the sampling rate (3 ms), the rate of the included impulse (1%), and the maximum size of the impulse (100 cm). Also, considering the length of the human arm and the development of the localization estimation, the radius and error of localization are set to 50 cm and 3 cm, respectively. The remaining elements were selected arbitrarily because they can vary depending on the installation environment and the characteristics of the system. Preprocessing is used in order to minimize the errors of localization acquired from a mobile node. In other words, if the error is 0 cm, the azimuth error for the proposed method is 0°. Figure 5 presents the performance of the cumulative average error when the experiments were repeated up to 100 times for the general WFs and the proposed IWAF. For the general WF used as a preprocessing step, the impulse noise is reduced more for α = 0.9 than α = 0.1 or α = 0.5, and the performance of the general WF (α = 0.9) represents an average error of 5.09°. Meanwhile, for the proposed IWAF, the average error is 2.5°. The performance improves by about a factor of two compared to the WF (α = 0.9) because the droop phenomenon does not exist, and the impulse noise is effectively reduced. Furthermore, it is confirmed that the relative azimuth estimation algorithm effectively obtains the azimuth in a localization system that contains an error. In an indoor navigation system, the proposed algorithm provides reliable orientation information to a user without using an azimuth sensor that is vulnerable to magnetic interference.

Figure 5:

Cumulative average error when the experiments were repeated n times

4. Conclusion

This paper proposed an algorithm that estimates the relative azimuth using rotational displacement information of a mobile node when a user grabs the node and rotates it. The proposed technique may be applied to precise localization systems to guide a user in the right direction by estimating the relative azimuth without using any sensors that are affected by magnetic fields. Before the rotational displacement algorithm is applied, an IWAF is used to effectively reduce the impulse noise, which can affect the accurate determination of the azimuth, without large computational costs. Then a stable accumulated error, even after several repetitions, is obtained with time. Thus, navigation operates with the proposed algorithm in the indoor environments, where a variety of electromagnetic interference via electronic devices or power lines exists, with reliable and effective route guidance.

Acknowledgments

This work is the outcome of a Manpower Development Program for Marine Energy by the Ministry of Oceans and Fisheries and the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (No. 20110029766).

References

• I. D'Souza, W. Ma, and C. Notobartolo, “Real-time location systems for hospital emergency response”, IEEE IT Professional, 13(2), p37-43, (2011). [https://doi.org/10.1109/MITP.2011.31]
• H.-T. Cho, T.-W. Kim, Y.-J. Park, and Y.-J. Baek, “Enhanced trajectory estimation method for RTLS in port logistics environment”, High Performance Computing and Communication & 2012 IEEE 9th International Conference Embedded Software Systems (HPCC-ICESS), p1555-1562, (2012). [https://doi.org/10.1109/HPCC.2012.227]
• H.-J. Cho, K.-I. Hwang, D.-S. Noh, and D.-H. Seo, “Real time indoor positioning system using IEEE 802.15.4a and sensors”, Journal of the Korean Society of Marine Engineering, 36(6), p850-856, (2012), (in Korean). [https://doi.org/10.5916/jkosme.2012.36.6.850]
• J.-H. Seong, T.-W. Lim, J.-S. Kim, S.-G. Park, and D.-H. Seo, “An improvement algorithm for localization using adjacent node and distance variation analysis techniques in a ship”, Journal of the Korean Society of Marine Engineering, 37(2), p213-219, (2013), (in Korean). [https://doi.org/10.5916/jkosme.2013.37.2.213]
• H.-J. Cho, J.-S. Kim, S.-G. Lee, J.-W. Kim, and D.-H. Seo, “Fixed node reduction technique using relative coordinate estimation algorithm”, Journal of The Korean Society of Marine Engineering, 37(2), p220-226, (2013), (in Korean). [https://doi.org/10.5916/jkosme.2013.37.2.220]
• J.-H. Seong, J.-S. Park, S.-H. Lee, and D.-H. Seo, “Indoor localization algorithm based on WLAN using modified database and selective”, Journal of The Korean Society of Marine Engineering, 37(8), p932-938, (2013). [https://doi.org/10.5916/jkosme.2013.37.8.932]
• C. Fischer, and H. Gellersen, “Location and navigation support for emergency responders: A survey”, IEEE Pervasive Computing, 9(1), p38-47, (2010). [https://doi.org/10.1109/MPRV.2009.91]
• Y. Chon, and H. Cha, “LifeMap: a smartphone-based context provider for location-based services”, IEEE Pervasive Computing, 10(2), p58-67, (2011). [https://doi.org/10.1109/MPRV.2011.13]
• J. Fujimoto, S. Hotta, K. Sawada, Y. Hada, K. Hida, and S. Mori, “Hybrid positioning system combining spatially continuous and discrete information for indoor location-based service”, Ubiquitous Positioning, Indoor Navigation, and Location Based Service (UPINLBS), p1-6, (2012). [https://doi.org/10.1109/UPINLBS.2012.6409774]
• B.-G. Lee, and W.-Y. Chung, “Multitarget three-dimensional indoor navigation on a PDA in a wireless sensor network”, IEEE Sensors Journal, 11(3), p799-807, (2011). [https://doi.org/10.1109/JSEN.2010.2076802]
• A. R J. Ruiz, F. S. Granja, J. C. Prieto Honorate, and J. I. G. Rosas, “Accurate pedestrian indoor navigation by tightly coupling foot-mounted IMU and RFID measurements”, IEEE Transactions on Instrumentation Measurement, 61(1), p178-189, (2012).
• R. Zhang, and L. M. Reindl, “Pedestrian motion based inertial sensor fusion by a modified complementary separate bias Kalman filter”, IEEE Sensors Applications Symposium (SAS), p209-213, (2011). [https://doi.org/10.1109/SAS.2011.5739766]
• R. Zhang, F. Hoflinger, and L. Reindl, “Inertial sensor based indoor localization and monitoring system for emergency responders”, IEEE Sensors Journal, 13(2), p838-848, (2013). [https://doi.org/10.1109/JSEN.2012.2227593]
• S. E. Umbaugh, Computer Vision and Image Processing, Prentice-Hall, Englewood Cliffs, NJ, USA, (1998).
• H. S. Yazdi, and F. Homayouni, “Impulsive noise suppression of images using adaptive median filter”, International Journal of Signal processing Image Processing and Pattern Recognition, 3(3), p1-12, (2010).
• T.-C. Lin, “A new adaptive center weighted median filter for suppressing impulsive noise in images”, Information Sciences, 177(4), p1073-1087, (2007). [https://doi.org/10.1016/j.ins.2006.07.030]