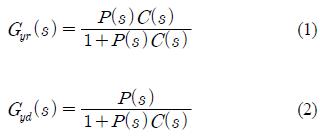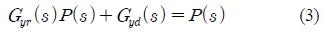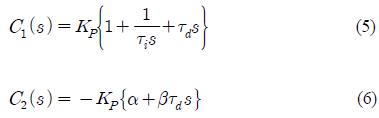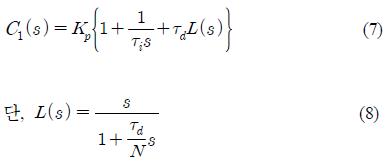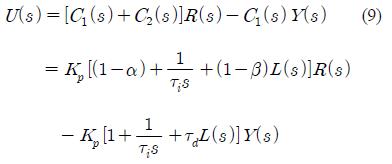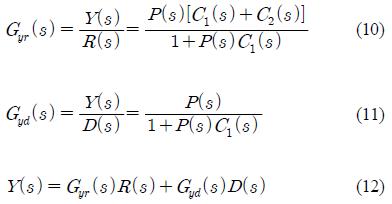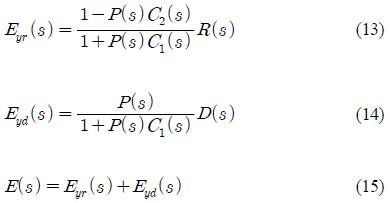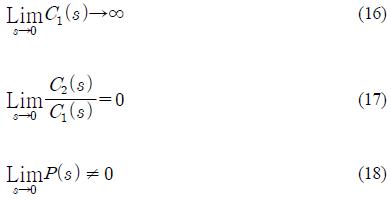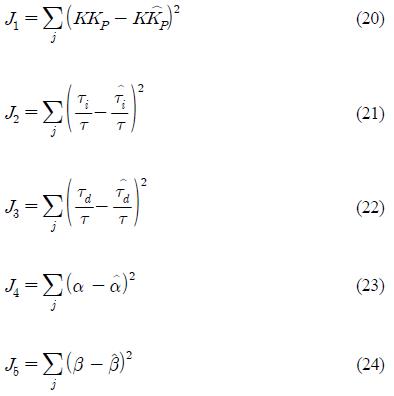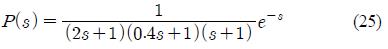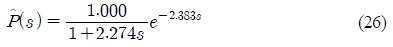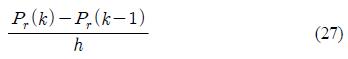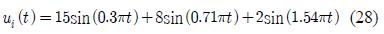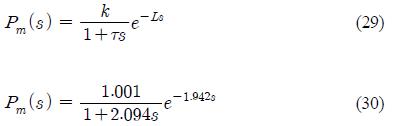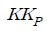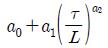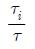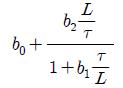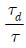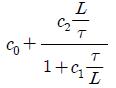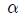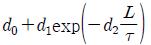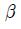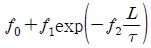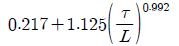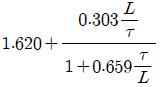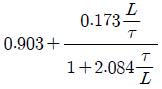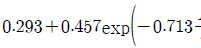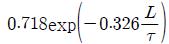A study on the optimal tuning of the hydraulic motion driver parameter by using RCGA

2.1 기존의 PID 제어기의 한계

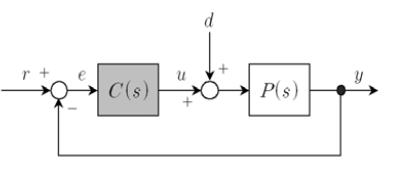
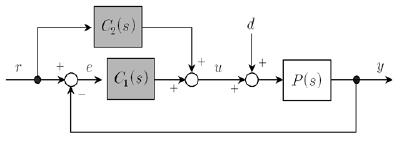
Figure 1은 기존의 PID 제어기의 구조를 나타낸 것이다.

Figure 1:

Conventional PID control system

여기서, r; 설정치, y; 플랜트 출력, d; 외란, C(s); PID 제어기 전달함수, u;제어기 출력, P(s) ;플랜트 전달함수를 의미한다.

r에 대한 출력 y의 전달함수 G_yr(s)와 외란 d에 대한 출력 y의 전달함수 G_yd(s)는 다음과 같이 주어진다.

여기서, 첨자 yr은 d = 0인 경우의 입출력 신호를, yd는 r = 0인 경우의 입출력 신호를 의미한다.

사용자는 만족할 만한 출력 y를 얻기 위해서는 G_yr(s)와 G_yd(s) 2개의 전달함수를 각각 최적화 하여야 한다. 그러나 2개의 전달함수는 서로 상관관계에 있으므로 각각의 전달함수를 독립적으로 최적화 하는 것은 불가능하며, 오직 C(s)의 제어인자만이 사용자에 의한 튜닝이 가능하다. 2개의 전달함수에서 C(s) 치환을 통해 상관관계를 살펴보면 그 한계가 명확해진다.

플랜트의 전달함수인 P(s)가 주어질 때, 원하는 설정치에 빠르게 추종하도록 G_yr(s)를 최적화시키면 G_yd(s)도 결정되므로 외란 억제성능이 떨어지고, 반대로 외란 억제성능이 향상되도록 G_yd(s)를 최적화 시키면 G_yr(s)가 임의의 형태로 고정되어 설정치 추종성능이 나빠진다. 운전조건이 다양한 플랜트는 고차원적이고 비선형적인 동특성을 가지고 있지만, 대부분의 고차원적 제어특성을 갖는 플랜트는 시간지연 요소를 가지는 1차원적 시스템으로 간소화 시킬 수 있기 때문에 식 (4)와 같은 시간지연 요소를 가지는 1차원적 시스템의 시뮬레이션을 통해 한계점을 확인할 수 있다.

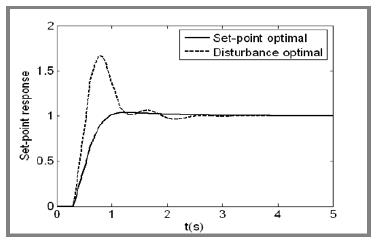
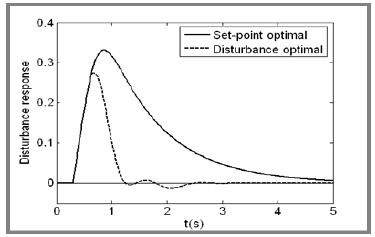
제어기 C(s)의 제어인자는 Table 1에 보이는 바와 같고, 시뮬레이션을 위한 MATLAB의 블록선도는 Figure 2에 보이는 바와 같으며, 이 때의 단위입력 응답과 단위외란 응답은 각각 Figure 3과 Figure 4에 보인다.

Table 1:

Parameters 1th order time delay system

Figure 2:

Block diagram of PID controller

Figure 3:

Disturbance of set point

Figure 4:

Disturbance of response

Figure 3과 Figure 4에서 실선은 설정치 추종성능이 양호한 제어인자를 설정한 결과이며, 점선은 외란 억제성능이 개선되도록 제어인자를 설정한 결과이다.

설정치 추종성능이 개선되도록 제어인자를 설정한 경우 설정치 추종속도는 빠르나, 외란 입력시 정상상태로 복귀하는데 매우 느리며, 반대로 외란 억제성능이 개선되도록 제어인자를 설정한 경우 외란이 가해졌을 때는 신속하게 정상상태로 돌아오지만, 단위입력에 추종하는 속도는 상대적으로 느리고 상당한 오버슈트가 발생되는 것으로 보아 기존 PID 제어기의 한계가 드러난다.

2.2 2DOF PID 제어기

2DOF PID 제어기는 기존의 PID 제어기 형태의 주제어기 전달함수 C₁(s)와 피드-포워드 게인의 전달함수 C₂(s)로 이루어진다. 이러한 제어기의 튜닝은 먼저 주제어기를 튜닝한 후 피드-포워드 제어기를 튜닝하는 순서로 이루어진다.

여기서, C₁(s)와 C₂(s)는 2DOF PID 제어기 전달함수이며 다음과 같이 유도된다.

기존의 PID 제어기의 전달함수는 식 (5) 및 식 (6)에 보이는 바와 같이 K_Pτ_Ds형태의 미분성분이 포함되어 있어서 설정치나 외란이 급격하게 변할 때, 플랜트에 입력되는 제어기 출력 u를 지나치게 크게할 우려가 있기 때문에 이를 방지하기 위해 식 (7)에 보이는 바와 같이 미분동작의 필터링 효과를 주는 여과함수 N을 추가하였으며, 이것은 제어환경에 따라 경험적으로 10에서 100사이에서 결정될 수 있다[8].

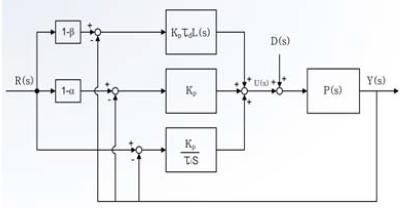
한편, Figure 5에 보인 제어기 출력함수 u(s)는 식 (9)으로부터 구할 수 있으며, 이를 블록선도로 표시하면 Figure 6에 보이는 바와 같다.

Figure 5:

2DOF PID control system

Figure 6:

Equivalent 2DOF PID control system

식 (9) 및 Figure 6에 보인 제어기 출력은 설정치 R(s)와 출력 Y(s)에 연결되어 있고, 특히 (1 - α)와 (1 - β)는 R(s)에 연결되어 있는 PID 제어기의 비례요소와 미분요소의 강도(Strength)를 뜻한다. 일반적으로 α와 β는 0과 1사의 값을 가지며, 표준 PID 제어기는 α = 0와 β = 0을 갖는 2DOF PID 제어기의 특별한 형태임을 알 수 있다.

Figure 6 및 식 (5)로부터 2DOF PID 제어기의 설정치 입력 r에 대한 출력 y의 전달함수 G_yr(s)와 외란입력 d에 대한 출력 y의 전달함수 G_yd(s)는 다음과 같이 주어진다.

한편, 상기 전달함수에서 각각의 오차 E_yr(s)와 E_yd(s)와 전체 오차는 아래와 계산식으로 구한다.

식 (13) 내지 식 (14)에서 아래의 조건 식 (16) 내지 식 (18)를 만족하면 단위입력의 설정치 변경과 외란 변경에 정상편차가 0이 되므로, 본 연구에서 개발한 제어시스템은 이 조건을 모두 만족하는 것으로 보아 단위입력의 설정치 또는 외란 변경에 정상편차가 발생되지 않음을 확인할 수 있다.

입·출력을 구하는데 사용되는 식 (10) 내지 식 (12)에 서의 출력은 설정치 입력에 대한 응답과 외란 입력에 대한 응답의 선형결합이며, 설정치 입력에 대한 응답은 피이드백 보상과 피드포워드 보상이 결합되어 있다. 특히 외란 입력에 대한 응답은 C₂(s)와는 무관하므로 C₁(s)의 제어인자를 최적 동조시킨 후 이 값을 이용하여 다시 피드포워드 보상요소인 C₂(s)의 매개변수를 동조시킬 수 있다. 이와 같이 함으로서 설정치응답 전달함수인 G_yr(s) 외란응답 전달함수인 G_yd(s)를 독립적으로 최적화시켜서 기존의 PID 제어기가 가지는 한계를 극복하여 설정치 추종성능과 외란 억제성능을 동시에 만족시킬 수 있다.

3.1 2DOF PID 제어기 동조

2DOF PID 제어기는 K_P, τ_i, τ_d, α, β 등 5개의 제어인자를 구비하며, 모델과 RCGA를 기반으로 동조되고 미분동작부의 필터링효과 N은 제어환경에 따라 경험적으로 1~100 사이에서 결정될 수 있다. 여러 가지 시뮬레이션을 통해 본 연구에서는 N을 “10”으로 선정하였으며, 그 과정은 아래와 같다.

① 필터링 효과 N을 경험적으로 결정

② 최적화를 위한 우수한 감도의 성능지수 선택

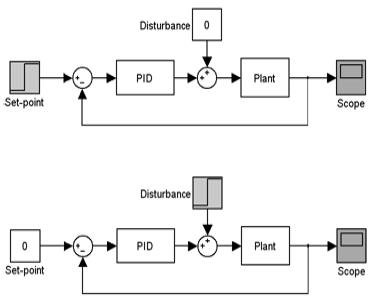
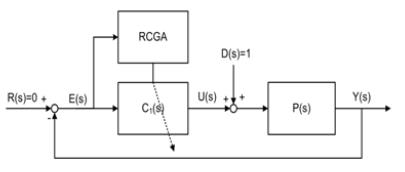
③ 설정치 입력을 “0”으로 유지한 상태에서 RCGA를 이용하여 외란 억제성능이 양호하도록 C₁(s)를 구성하는 {K_P, τ_i, τ_d}를 최적화

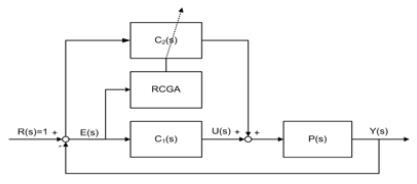
④ 외란을 “0”으로 유지하고, C₁(s)를 고정한 상태에서 RCGA를 이용하여 설정치 추종성능이 양호하도록 C₂(s)의 {α, β}를 최적화

Figure 7은 RCGA와 제어대상의 모델을 기반으로 C₁(s)의 제어인자 K_P, τi, τd를 최적 동조하는 과정을 보여주고 있으며, 이때 목적함수는 식 (19)의 ITAE를 사용하였다. 모델의 제어인자 추정에서 RCGA는 시스템출력과 모델 출력의 오차 e(t) = y(t) - y_m(t)의 절대값과 시간에 대한 적분값이 최소가 되도록 제어기의 제어인자를 조정한다. 이 때 r(t)으로 고정된다.

Figure 7:

C1(s) Parameter tuning using RCGA

여기서, ϕ = [K_P T_i T_d]^T, t_f;최종적분 시각으로 t_f 이후의 적분 값을 무시해도 좋을 정도로 충분한 시간이다.

Figure 8은 RCGA와 제어대상의 모델을 기반으로 C₂(s)의 제어인자 α, β를 최적 동조하는 과정을 보여주고 있으며, 이때 목적함수는 식 (19)의 ITAE를 사용하였다. 모델의 제어인자 추정에서 RCGA는 설정치와 출력의 오차 e(t) = r(t) - y(t)의 절대 값과 시간에 대한 적분 값이 최소가 되도록 제어인자를 조정한다.

Figure 8:

C2(s) Parameter tuning using RCGA

Figure 8:

PID parameter tuning using a RCGA

여기서 ϕ = [{α,β]^T 이다.

3.2 동조규칙의 유도

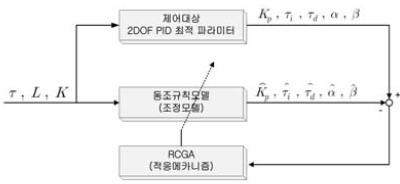
3.1절에서 구한 최적의 제어인자 2DOF PID 제어기의 계수 집합을 이용하여 Figure 9의 블록선도로부터 새로운 동조규칙을 얻는다.

최적의 2DOF PID 최적 제어인자와 동조규칙 모델의 결과가 서로 동일하게 동조규칙의 모델 파라메타를 최적화한다. 이때 사용되는 동조규칙 모델은 기존의 연구결과를 참고하여 다양한 형태의 모델을 적용한 결과 가장 근사한 형태의 모델을 사용하였다.

최적의 동조규칙 모델을 찾기 위해 RCGA를 이용하였으며, 아래의 성능지수가 최소가 되도록 하였다.

성능지수로서는 오차 제곱의 적분인 ISE 방법을 선택하였다. ISE는 계수집단을 토대로 전체를 아우르는 근사곡선을 구할 경우, 큰 폭의 오차에 대해 보다 더 큰 벌점 부여함으로서 다양한 계수들의 경우에도 보다 변동 폭이 적은 근사곡선을 구하기 위한 것이다. 참고문헌과 기존 연구결과를 참고하여 동조규칙 모델은 Table 2와 같다.

Table 2:

Tuning rule models

Table 3:

2DOF PID controller tuning rules

앞의 과정을 통해 구해진 2DOF PID 제어기를 위한 최적의 동조규칙 모델은 Table 2에 보인다. 이로서 제어대상의 매개변수 K, τ, L을 구하면 이 동조규칙을 이용하여 최적의 2DOF PID 계수를 용이하게 구할 수 있다.

4.1 시뮬레이션을 위한 시스템 I

먼저 식 (25)과 같은 시간 지연 요소를 갖는 3차 시스템을 고려하였다.

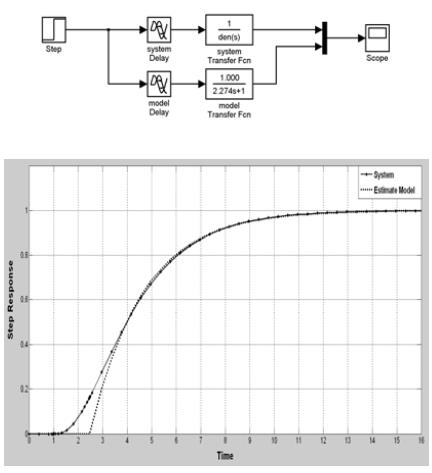
시스템 식 (25)을 식 (5)의 제어대상과 같은 형태로 표현하기 위해 RCGA를 이용하여 0 ≤, τ, L ≤ 10의 구간에서 탐색을 진행하고, 샘플링 시간은 h = 0.01로 설정하여 근사치를 구하는 모델식은 식 (26)과 같다.

위의 모델 식 (26)과 주어진 시스템 식 (25)이 유사한 시스템인지 확인하기 위해 매트랩 시뮬링크를 이용하여 단위계단 입력을 부여하고, 시스템과 모델의 응답은 Figure 9에 보이는 바와 같이 근사화한 모델과 시스템이 거의 유사함을 확인할 수 있다.

Figure 9:

Responses of system & estimated model

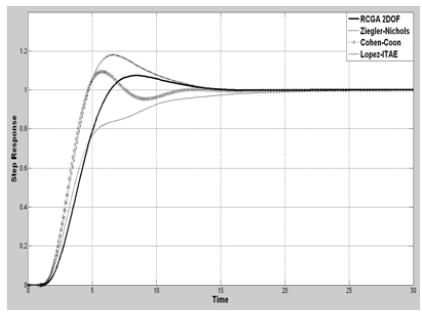
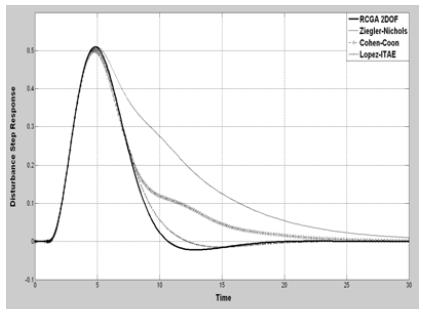
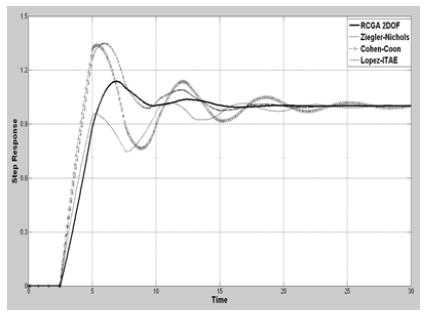
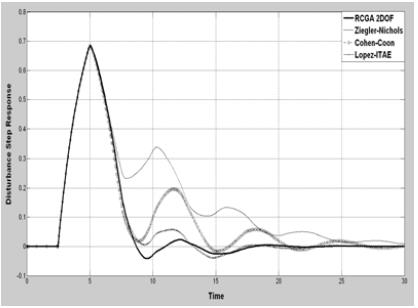
추정된 모델을 대상으로 기존의 동조규칙과 본 논문에서 제안한 RCGA를 이용한 2DOF PID 제어기 동조규칙을 통해 제어인자를 계산하고, 각각의 동조규칙에 따른 제어기의 성능을 확인하기 위해 모델에 외란과 단위계단 입력을 부가하여 시뮬레이션한 결과는 Figure 10 및 Figure 11에 보이는 바와 같다.

Figure 10:

Step response comparison

Figure 11:

Disturbances of step response

Figure 10 및 Figure 11에서 Ziegler Nichols 동조규칙의 경우 목표치 추종성능에서 비교적 작은 오버슈트와 빠른 정착시간을 보였지만 외란 억제성능이 미흡하였다. 이에 비해 외란 억제성능에서 양호한 모습을 보인 Lopez ITAE 동조규칙의 경우 단위계단입력 인가 시 높은 오버슈트와 함께 정착시간이 비교적 길게 측정되었으나, 2DOF PID 제어기의 경우 단위계단입력에 대한 목표치 추종성능과 단위계단외란에 대한 외란 억제성능 모두 양호한 형태를 보여주었다.

4.2 유압 모션제어기 시뮬레이션

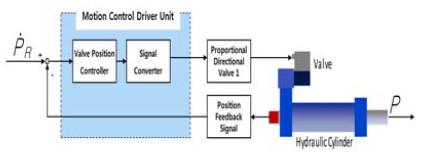
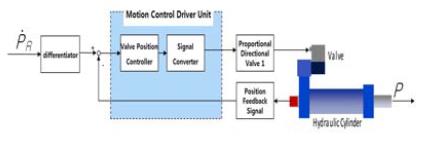
제어밸브의 구동부에 장착된 유압 모션 제어기는 다음과 같은 블록선도로 나타낼 수 있다.

제어밸브시스템을 구성하는 유압 모션 제어기는 이미 내부에 비례제어밸브를 유체동력으로 구동하기 위한 신호로 변환해주는 장치가 내장되어 있다. 특히 위치제어기를 포함하고 있어서 사용자는 원하는 위치만 설정하면 제어밸브시스템에 부착된 제어밸브의 부하 모멘트가 변경되어도 적절한 유체동력을 비례제어밸브로 출력한다. 따라서 직선운동시스템의 전달함수에서 부하모멘트가 무시해도 될 정도로 작다. 입력값과 출력값의 차원이 서로 다르므로, 입력단에 식 (27)과 같은 미분기를 두어, 입력값과 출력값의 차원을 동일하게 나타낸 블록선도는 Figure 12에 보인다.

Figure 12:

Bloc diagram of hyd. motion controller

여기서, P_r; 설정 값, k; 현재 시간, h; 샘플링 시간을 의미한다.

Figure 13:

Hydraulic motion controller with differentiator

미분기를 포함하는 변형된 유압구동 엑튜에이터 제어기의 전달함수는 내부에 폐회로형 위치제어기가 포함되어 있어 전달함수의 수학적 모델링이 쉽지 않다. 따라서 시스템의 입출력 신호를 파악하기 위해 식 (28)와 같은 정현신호의 조합을 입력하고, 그에 따른 출력을 관찰하여 확률적으로 그 전달함수를 추정하는 방법을 취한다.

대부분의 고차시스템은 1차 지연함수와 시간지연의 결합으로 근사화 할 수 있다. 유압 모션 제어기의 전달함수를 식 (29)으로 가정하고 RCGA를 통해 근사화한 모델의 전달함수는 식 (30)과 같다.

제안한 동조규칙의 성능을 확인하기 위해 모델로 표현된 제어밸브시스템의 유압모션 제어기의 단위계단 입력과 외란 입력을 인가한 결과는 Figure 14 및 Figure 15에 보이는 바와 같다.

Figure 14:

Step response comparison

Figure 15:

Disturbance response comparison