가변형 APF를 이용한 단상 영구자석 동기전동기의 DQ모델 기반 기동운전에 관한 연구

1. 서 론

영구자석 동기전동기는 회전자가 영구자석으로 이루어져 회전자의 철손 성분이 없고, 높은 자속 밀도를 가지기 때문에 높은 효율을 유지한다. 그리고 직류 전동기보다 출력 밀도가 높아 큰 토크를 출력할 수 있으며, 속응성이 좋다는 장점을 가지고 있다. 또한, 고효율 및 제어 특성이 우수하며 소형화 측면에서 유리한 측면이 있다. 전력전자 기술의 발전과 함께 기존의 유도 전동기 및 직류 전동기가 사용되던 일반적인 산업 분야 이외에 가정기기에서도 그 쓰임이 빠르게 확대되고 있는 추세이다[1][2].

이로 인해 본 논문의 대상 전동기인 단상 영구자석 동기전동기는 3상 영구자석 동기전동기와 비교하면 상대적으로 토크 리플이 크고 운전 성능이 낮지만, 구동을 위한 인버터 구성 및 위치 센서의 부착 등에 따라 주변소자의 수량과 설치 공간 감소, 자유로운 전동기 철심의 형상 변화를 통해 저전력 소형화 및 모듈화가 가능하여 저가격화 및 부피 감소, 제어 용이성, 간단한 구동회로 구성 등을 만족한다. 따라서 소형의 펌프, 블로워, 청소기 등과 같은 소형화 및 휴대용 제품에 유리하다[3].

일반적으로 단상 영구자석 동기전동기는 자기적 구조로 인해 입력 전원을 인가할 경우, 토크가 ‘0’인 Dead point가 발생한다. 따라서 이러한 현상을 보완하기 위하여 고정자 치와 회전자 간에 공극 길이의 차이를 둔 비대칭 공극을 통하여 Dead point를 제거한다. 그러나 비대칭 공극을 적용하였을 경우, 소음 및 진동의 원인 중 하나인 코깅 토크가 발생할 수 있으므로 고정자 형상에 따른 역기전력과 코깅 토크 특성 변화를 고려하여야 한다[4][5]. 이와 함께 영구자석 동기전동기는 자석의 위치가 회전자에 고정되어 있기 때문에 벡터제어를 위해서는 위치 센서를 통하여 회전자 위치 정보를 얻는 것이 필수적이다. 하지만, 위치 센서는 고가이며, 위치 센서를 취부하기 위한 추가적인 설치 공간 확보가 필요하고, 제품을 소형화함에 있어 큰 제약조건이 될 수 있다. 특히, 냉장고나 에어컨 등의 가전제품에 대한 핵심 부분인 압축기 구동용으로 사용되는 경우에는 사용 환경상 위치 검출용 센서를 설치하기 매우 곤란한 경우도 있다. 이를 위해 영구자석 동기전동기 구동을 위한 다양한 센서리스 운전기법이 수년간 많이 진행되고 있다. 대표적인 3상 영구자석 동기전동기의 센서리스 운전 방식은 크게 전동기의 수학적 모델을 기반한 선형 모델 기법과 전동기의 구조 차이에 의한 비선형 모델 기법으로 구분할 수 있다. 대표적인 선형 모델 기법은 중/고속 운전 시 용이한 역기전력 또는 자속 기반 방식이며, 비선형 모델 기법은 정지 및 저속 영역에서 회전자 위치 검출이 용이한 신호 주입 방식이 있다[6][7]. 이와 같이 3상 영구자석 동기전동기의 위치 및 속도 추정에 관한 수많은 논문이 발표되었지만, 단상 영구자석 전동기는 동일한 수준의 연구 성과에 미치지 못했다. 단상 영구자석 동기전동기 센서리스 제어 기법으로는 권선 시간 공유 방식을 통한 역기전력을 측정하는 것을 기반으로 센서리스 제어를 수행하는 방식이 있다[8]. 앞서 언급한 역기전력 기반 센서리스 제어는 영속 및 저속 영역에서 역기전력의 크기가 미소하여 정확한 위치를 추정하는데 어려움이 있다. 따라서 본 논문에서는 단상 영구자석 동기전동기의 센서리스 제어를 오픈 루프 운전 영역인 정지 및 저속 영역에서 안정적인 기동 운전 특성을 확보하기 위하여 가변 차단 주파수를 갖는 전역통과필터를 이용한 가상 DQ모델 기반 기동 알고리즘을 제안하고 실험을 통한 알고리즘의 타당성을 검증한다.

2. 단상 영구자석 동기전동기의 모델링

2.1 단상 영구자석 동기전동기의 수학적 모델

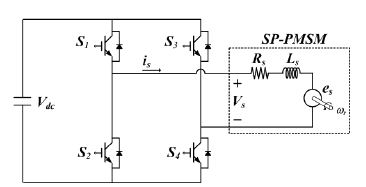
단상 영구자석 동기전동기의 등가 회로도는 Figure 1와 같으며, 이에 대한 고정자 전압 방정식은 고정자 권선과 회전자의 계자가 서로 독립적이므로 식 (1)과 같이 고정자 권선 저항에 대한 전압 강하성분과 고정자 권선에 쇄교하는 자속 λ의 시간당 변화율의 합으로 표현할 수 있다.

Figure 1

Full-bridge circuit of single-phase PMSM

$\[ {\upsilon }_s=R_s{i}_s+\frac{d\lambda }{dt} \]$

(1)

여기서, υ_s는 고정자 권선의 전압, R_s는 고정자 권선 저항, λ는 고정자 권선에 쇄교하는 자속을 나타낸다.

고정자 권선의 쇄교자속은 영구자석에 의한 쇄교자속과 고정자 전류에 의한 쇄교자속으로 표현할 수 있다.

$\[ \lambda ={\lambda }_s+{\lambda }_{PM} \]$

(2)

여기서, λ_PM은 영구자석에 의한 쇄교자속, λ_s는 고정자 전류에 의한 쇄교자속을 나타낸다.

식 (2)의 고정자 쇄교자속은 식 (3)과 식 (4)의 자속 성분들로 구성됨을 보여주고 있다.

$\[ {\lambda }_{PM}=K_e\text{cos}{\theta }_r \]$

(3)

$\[ {\lambda }_s=L_s{i}_s \]$

(4)

여기서, K_e는 역기전력 상수, L_s는 고정자 인덕턴스, i_s는 고정자 전류, θ_r는 회전자 위치각을 나타낸다.

식 (1)에 식 (2), 식 (3) 및 식 (4)를 대입하여 고정자 전압 방정식을 정리하면 식 (5)와 같이 나타낼 수 있다.

$\[ {\upsilon }_s=R_s{i}_s+L_s\frac{{di}_s}{dt}-K_e{\omega }_r\text{sin}{\theta }_r \]$

(5)

여기서, ω_r는 회전자 전기 각속도를 나타낸다.

풀 브릿지 인버터의 손실을 무시하고 단상 영구자석 동기전동기에 입력되는 순시전력을 정리하면 식 (6)과 같다.

$\[ P_{in}={\upsilon }_s{i}_s=R_s{i}_s^2+L_s{i}_s\frac{{di}_s}{dt}+e_s{i}_s \]$

(6)

여기서, e_s는 단상 영구자석 동기전동기의 역기전력, P_in는 단상 영구자석 동기전동기에 입력되는 순시전력을 나타낸다. 식 (6)에서 첫 번째 항은 동손, 두 번째 항은 자계 에너지의 변화분을 뜻하며, 마지막 항은 기계적 출력을 의미한다.

$\[ e_s={-E}_m\sin {\omega }_{r}t, i_s={-I}_m\sin {\omega }_{r}t \]$

(7)

$\[ P_{out}=\frac{E_m{I}_m}{2}-\frac{E_m{I}_m}{2}\mathit{cos}{2\omega }_{r}t \]$

(8)

여기서, E_m은 단상 영구자석 동기전동기의 역기전력 최대값, I_m는 고정자 입력전류의 최대값, P_out은 기계적 출력을 나타낸다.

전기적 출력 토크에 의한 운동 방정식은 식 (9)와 같이 정의된다.

$\[ T_e=J_m\frac{{d\omega }_m}{dt}+B_m{\omega }_m+T_L \]$

(9)

여기서, J_m은 단상 영구자석 동기전동기의 관성 모멘트, B_m은 단상 영구자석 동기전동기의 점성 마찰 계수, ω_m는 회전자 기계각 속도, T_L는 부하 토크를 나타낸다.

2.2 가상 DQ 모델 기반 회전자 좌표계 모델 방정식

본 논문에서 단상 영구자석 동기전동기의 센서리스 운전 시 원활한 전류 및 속도제어를 위하여 3상 동기전동기의 벡터제어에 적용되는 좌표변환 개념을 이용하고자 한다. 회전자 좌표계 모델은 시스템의 순시제어가 가능하고 제어변수가 직류값이므로 제어 및 필터링 과정에서 장점을 가진다. 또한, dq축의 직교하는 두 성분으로 분리할 수 있기에 유효 및 무효전력 제어, 고속 운전에 따른 디지털 시지연의 보상이 유리하다.

단상 영구자석 동기전동기를 정지 좌표계 모델로 나타내기 위해서는 가상의 q축 모델이 필요하다. 이를 위해서 계통연계형 단상 시스템에 널리 적용되는 전역통과필터의 특성을 이용하여 고정자 전류에 대한 가상의 q축 전류를 생성하고자 한다[9].

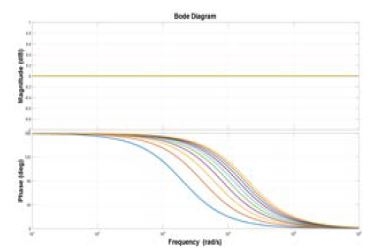
전역통과필터의 특징은 전동기의 운전 주파수 증가에도 불구하고 차단 주파수에서 실제전류인 d축 전류의 크기 감쇄없이 90° 위상 지연이 발생된다.

전역통과필터의 전달함수는 식 (10)과 같이 정의된다.

$\[ G_{APF}\left(s\right)=\frac{{\omega }_{\upsilon ar}-s}{{\omega }_{\upsilon ar}+s} \]$

(10)

여기서, ω_υar는 단상 영구자석 동기전동기의 운전속도에 따른 전역통과필터의 가변 차단 주차수를 나타낸다.

전역통과필터는 Figure 2와 같이 차단 주파수를 가변 시킴에 따라 전동기의 가변속 운전 시에도 전류가 90° 지연됨을 보여주고 있다. 이를 토대로 안정적인 dq축 전류제어를 수행할 수 있다.

Figure 2

Bode plot of all-pass filter with variable frequency

단상 영구자석 동기전동기의 고정자 전류 i^s_ds를 전역통과필터의 특징을 이용한 가상의 전류 i^s_qs는 식 (11)처럼 나타낼 수 있다.

$\[ i_{ds}^s={-I}_m\sin {\theta }_r, i_{qs}^s=I_m\cos {\theta }_r \]$

(11)

앞서 언급한 전역통과필터를 이용한 고정자 전류 및 가상의 전류 정보를 이용하여 회전자의 속도에 동기화하여 회전하는 회전자 좌표계로의 변환은 3상 시스템과 같은 방법으로 구현할 수 있다. 어떤 벡터를 ω_rt만큼 회전 시키는 벡터를 식 (12)와 같이 정의할 수 있다.

$\[ T\left({\omega }_{r}t\right)=\left[\begin{array}{cc}\text{cos}{\theta }_r& \text{sin}{\theta }_r\\ \text{-sin}{\theta }_r& \cos {\theta }_r\end{array}\right] \]$

(12)

여기서, T(ω_rt)는 변환행렬을 나타낸다.

d^s-q^s축 전류의 회전자 좌표계 변환은 식 (13)과 같이 나타낼 수 있다.

$\[ i_{dqs}^r=\left[\begin{array}{c}{i}_{ds}^r\\ i_{qs}^r\end{array}\right]=T\left({\omega }_{r}t\right)\left[\begin{array}{c}{i}_{ds}^s\\ i_{qs}^s\end{array}\right] \]$

(13)

d^s축을 실제 단상 시스템 축으로 가정한다면, 크기가 같고 위상이 90° 지연된 q^s축을 가상의 축으로 나타낼 수 있다. 이 축을 d^r-q^r축으로 변환 시킨 후 제어기의 출력을 다시 d^s-q^s축으로 역변환하여 이때 실제 존재하는 d^s축의 값을 고려할 수 있다. 따라서 q^s축의 물리적인 값은 존재하지 않으므로 벡터 제어를 위한 좌표변환만을 적용하기 위한 가상의 축이라고 할 수 있다.

단상 영구자석 동기전동기의 전압 방정식을 가상의 축 q^s축을 포함한 식으로 나타내면 식 (14)와 같다.

$\[ {\upsilon }_{dqs}^s=R_s{i}_{dqs}^s+L_s\frac{{di}_{dqs}^s}{dt}+e_{dqs}^s \]$

(14)

여기서, υ^s_dqs는 정지 좌표계 고정자 dq축 전압, i^s_dqs는 정지 좌표계 고정자 dq축 전류, e^s_dqs는 정지 좌표계 dq축 역기전력을 나타낸다.

위 전압 방정식을 회전자 좌표계로 변환하기 위하여 식 (14)의 양변에 변환행렬를 곱하면 식 (15)로 정리할 수 있다.

$\[ \left[\begin{array}{c}{\upsilon }_{ds}^r\\ {\upsilon }_{qs}^r\end{array}\right]=R_s\left[\begin{array}{c}{i}_{ds}^r\\ i_{qs}^r\end{array}\right]+L_s\frac{d}{dt}\left[\begin{array}{c}{i}_{ds}^r\\ i_{qs}^r\end{array}\right]+L_s\left[\begin{array}{cc}0& {-\omega }_r\\ {\omega }_r& 0\end{array}\right]\left[\begin{array}{c}{i}_{ds}^r\\ i_{qs}^r\end{array}\right]\left[\begin{array}{c}{e}_{ds}^r\\ e_{qs}^r\end{array}\right] \]$

(15)

출력 전압을 다시 d^s-q^s축으로 역변환한다. 이때 q^s축의 값은 물리적인 의미가 없는 가상 축의 전압이므로 고려하지 않고 d^s축의 전압, 즉 υ^r_ds값을 기준으로 PWM 수행하여 단상 영구자석 동기전동기에 전압을 인가하여 구동하게 된다. 역변환 행렬은 식 (16)과 같고, 역변환 식은 식 (17)과 같다.

$\[ T^{-1}\left({\omega }_{r}t\right)=\left[\begin{array}{cc}\text{cos}{\theta }_r& -\text{sin}{\theta }_r\\ \text{sin}{\theta }_r& \cos {\theta }_r\end{array}\right] \]$

(16)

$\[ {\upsilon }_{dqs}^s=\left[\begin{array}{c}{\upsilon }_{ds}^s\\ {\upsilon }_{qs}^s\end{array}\right]=T^{-1}\left({\omega }_{r}t\right)\left[\begin{array}{c}{\upsilon }_{ds}^r\\ {\upsilon }_{qs}^r\end{array}\right] \]$

(17)

2.3 가상 DQ 모델 기반 PI 전류 제어기

회전자 좌표계 dq축 전류 사이에는 상호 간섭 성분이 존재하며, 이로 인해 회전자 좌표계 dq축 전류의 변동이 상호간의 전류를 제어함에 있어 영향을 주게 된다. 따라서, 전류 제어기의 성능 향상을 위해서는 역기전력 성분과 함께 상호 간섭 성분에 대한 보상이 이루어져야 한다[10][11].

$\[ {\upsilon }_{dqs}^{r^{*}}={\upsilon }_{dqs,fb}^{r^{*}}+{\upsilon }_{dqs,ff}^{r^{*}} \]$

(18)

전류 제어기의 출력은 Limiter에 의해서 제한되며 Limiter 입력과 출력의 차는 안티 와인드업(Anti-windup)을 통하여 적분기에 연결함으로써 적분기의 와인드업 현상을 방지한다. 안티 와인드업을 포함한 전류 제어기는 식 (19)와 같다.

$\[ \begin{array}{l}{\upsilon }_{dqs,prop}^{r^{*}}=K_{pc}\left(i_{dqs}^{r^{*}}-i_{dqs}^r\right)\\ {\upsilon }_{dqs,i nteg}^{r^{*}}=K_{ic}\int \left(\left(i_{dqs}^{r^{*}}-i_{dqs}^r\right)+K_{ac}\left({\upsilon }_{dqs}^{r^{*}}-{\upsilon }_{dqs}^r\right)\right)dt\\ {\upsilon }_{dqs,fb}^{r^{*}}={\upsilon }_{dqs,prop}^{r^{*}}+{\upsilon }_{dqs,i n teg}^{r^{*}}\end{array} \]$

(19)

전향 보상된 역기전력 성분은 다음과 같다.

$\[ \begin{array}{l}{\upsilon }_{ds,ff}^{r^{*}}={-\omega }_r{L}_s{i}_{qs}^r\\ {\upsilon }_{qs,ff}^{r^{*}}={\omega }_r{L}_s{i}_{qs}^r+{\omega }_r{\lambda }_f\end{array} \]$

(20)

동기 좌표계 PI 전류 제어기의 비례 이득과 적분 이득을 식 (21)과 같이 설정하면 전류 제어기는 식 (22)와 같이 1차 저주파 통과 필터의 형태로 정리할 수 있다.

$\[ K_{pc}=L_s{\omega }_c, K_{ic}=R_s{\omega }_c \]$

(21)

$\[ \frac{i_{dqs}^r}{i_{dqs}^{r^{*}}}=\frac{{\omega }_c}{s+{\omega }_c} \]$

(22)

여기서 ω_c는 전류 제어기의 차단 주파수이다.

식 (22)와 같이 전류 제어기를 설정하면 오버슈트 없이 전류를 제어할 수 있다.

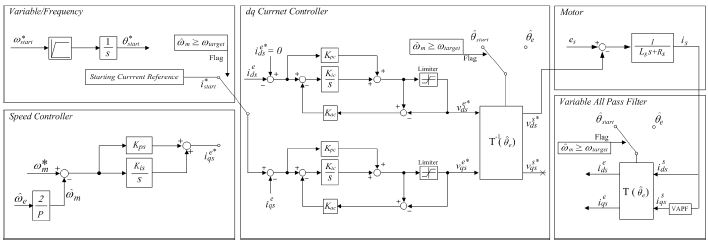
Figure 3과 같이 좌표 변환을 이용한 가상 dq축 모델 기반 전류 제어기를 단상 영구자석 동기전동기에 적용하였을 경우의 전체 블록도를 나타낸 것이다. 앞 절에서 언급한 바를 구하는 과정이 필요하다. 좌표 변환을 위한 회전자 위치각은 자속 기반 위치 추정기로부터 위치 정보를 얻는다. i^s_ds와 i^s_qs는 회전자 좌표계로 변환되어 전류 제어기를 거친 후 출력 전압 지령은 PWM을 수행하기 위해 d축 성분만을 취하여 PWM 수행하여 단상 영구자석 동기전동기에 전압을 인가하며 υ^s*_qs는 회전 좌표계로의 변환만을 위한 성분으로 물리적인 의미는 없다.

Figure 3

Control block diagram of starting algorithm based on synchronous reference frame PI current controller

3. 실험 및 결과

3.1 실험장치의 구성

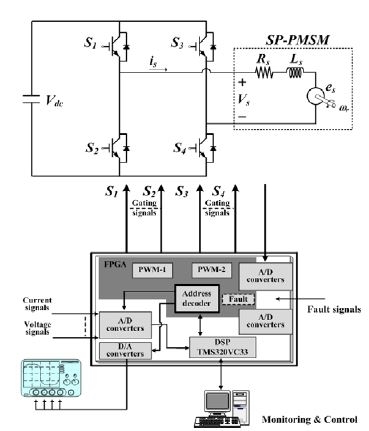
본 논문의 타당성을 입증하기 위해 Figure 4는 전체 실험장치의 블록도를 보여주고 있고 Figure 5는 실제 실험장치를 나타내고 있다. 여기서 실험장치는 크게 제어대상인 단상 영구자석 동기전동기, 풀 브릿지 인버터, 제어보드, 직류전원공급장치로 구성된다.

Figure 4

Block diagram of experimental setup

Figure 5

Block diagram of experimental setup

앞서 언급한 실험 대상 단상 영구자석 동기전동기 구동 시스템의 사양은 Table 1에 제시되어 있다.

Table 1

Specifications of Single-phase PMSM drive system

Table 1에서 단상 영구자석 동기전동기의 파라미터는 고정자 저항, 고정자 인덕턴스, 정격전압, 역기전력 상수가 표시되어 있고 풀 브릿지 인버터를 구성하는 요소들은 전류 센서 및 전압 센서, IGBT, Capacitor의 정격이 표시되어 있다. 이를 바탕으로 본 논문의 효용성 및 타당성을 증명하기 위해 실험을 하였다.

본 논문의 대상 전동기인 단상 영구자석 동기전동기의 가상 DQ축을 이용한 센서리스 기동 알고리즘의 타당성을 검증하기 위하여 정렬 시 성공 여부에 따른 전류파형의 변화를 살펴 볼 것이며 가변 차단주파수를 갖는 전역통과필터를 기반으로 한 가상 DQ축 PI 전류 제어기를 이용한 기동운전이 안정적으로 운전이 되고 있는지 검증하였다. 이를 위해, 10[kHz] 스위칭 주파수 및 제어 주기로 실험을 진행하였다.

3.2 V/f 기동

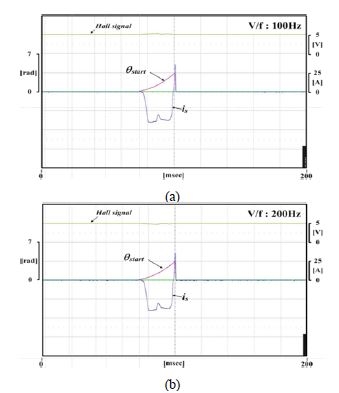
앞 절에서 언급한 단상 영구자석 동기전동기 구동 시스템의 사양인 Table 1에서 보이는 바와 같이 고정자 권선저항 R_s과 고정자 인덕턴스 L_s의 크기는 매우 작다. 따라서 단상 영구자석 동기전동기를 기동하기 위해 V/f 제어를 하였을 경우 고정자 권선에 과전류가 발생할 위험이 있다. 앞서 언급한 바와 같이 과전류가 발생할 경우 영구자석의 자력이 약해지는 감자현상이 발생할 수 있고 스위칭 소자 및 고정자 권선 등이 소손이 될 가능성이 있다. 따라서 본 논문에서는 전류를 직접 제어함으로써 앞서 언급한 감자현상 및 스위칭 소자와 고정자 권선 등의 소손을 제거하여 안정적인 기동을 확보할 수 있다. Figure 6은 V/f 제어를 통하여 전환 주파수가 100Hz, 200Hz의 조건에서 기동이 실패한 파형을 보여주고 있다.

Figure 6

Failed startup when using V/f control. (a) Changeover frequency 100[Hz]. (b) Change over frequency 200[Hz].

3.3 가상 DQ모델 전류 기동

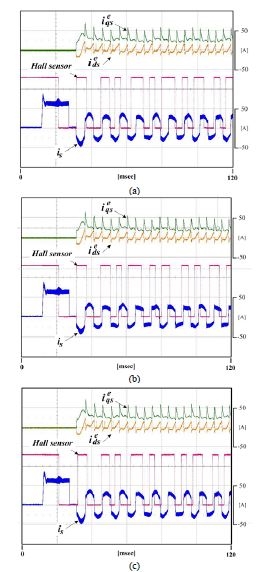
Figure 7과 Figure 8은 직류단 전압 및 기동 전류 변동에 따른 가상 DQ 모델 기반 PI 전류 제어기의 동작 특성을 보여주고 있다. 여기서, Figure 7과 Figure 8에서 보이는 바와 같이 고정자 전류 i_s의 파형이 정현파가 아닌 것을 볼 수 있다. 이는 단상 영구자석 동기 전동기의 기동시간 확보 및 정방향 운전을 위해서 스위칭 소자 및 데드 타임 등에 의한 전압 강하를 보상하기 위해서 지령전압에 구형파 전압을 반영한 결과이다. 그 결과 언급한 가변 차단주파수를 갖는 전역통과필터를 통해 90° 위상차를 가진 가상의 q축 전류를 발생시킬경우 Figure 7과 Figure 8에서 보이는 바와 같이 회전자 좌표계 및 정지 좌표계에서 전류 리플이 존재하는 것을 확인할 수 있다. 그러나 가상의 q축 전류는 단지 벡터제어를 위한 가상의 전류이므로 고려 대상에 포함되지 않는다. 따라서 본 논문에서는 고정자 전류에 전류의 리플은 있으나 직류단 전압 및 기동전류의 변화에도 불구하고 안정적으로 동작함을 확인할 수 있다.

Figure 7

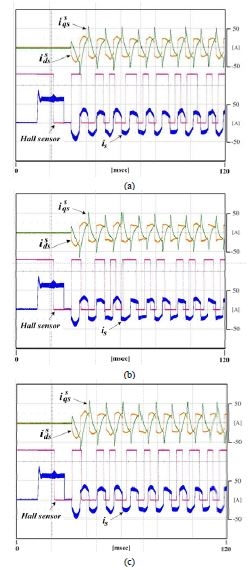
Stationary reference frame waveform of PI current controller based on virtual dq model. (a) Vdc=24[Vdc], Istart=30[A]. (b) Vdc=24[Vdc], Istart=25[A]. (c) Vdc=22[Vdc], Istart=30[A].

Figure 8

Synchronous reference frame waveform of PI current controller based on virtual dq model. (a) Vdc=24[Vdc], Istart=30[A]. (b) Vdc=24[Vdc], Istart=25[A]. (c) Vdc=22[Vdc], Istart=30[A].

4. 결 론

센서리스 제어 방식 중 모델 기반 센서리스 제어 방식은 영속 및 저속에서 회전자 속도에 비례하는 역기전력의 크기가 작으므로, 고속 운전용 단상 영구자석 동기전동기의 센서리스 운전시 요구되는 정지 및 저속 운전영역에서 역기전력 및 자속 추정에 한계가 있다. 따라서 본 논문에서는 자속기반 센서리스 운전시 요구되는 정지 및 저속 운전영역에서의 오픈 루프 기동 특성을 확보하기 위한 기동 알고리즘을 제안하였다. 영속 및 저속에서 오픈루프를 이용한 전류 제어를 통해 일정 속도까지 도달하기 위한 제안된 가상 DQ 모델 기반의 전류 제어를 적용하여 전류리플은 있으나 센서리스 적용 시점까지 안정적인 기동 운전이 가능함을 보였다. 이를 통하여 고속 운전용 단상 영구자석 동기전동기는 회전자 위치센서 없이 고속운전이 가능할 뿐만 아니라 구동 시스템의 부피 및 가격의 감소 효과를 얻을 수 있다.

Acknowledgments

본 논문은 2017년도 정부(교육부)의 재원으로 한국연구재단의 기초연구사업(NRF-2017R1D1A1B03 031807) 및 LG 전자 지원에 의하여 연구되었음.

References

• K. W. Lee, and J. I. Ha, “Evaluation of back-EMF estimators for sensorless control of permanent magnet synchronous motors”, Journal of Power Electronics, 12(4), p604-614, (2012). [https://doi.org/10.6113/jpe.2012.12.4.604]
• J. I. Ha, K. Ide, T. Sawa, and S. Sul, “Sensorless motor position estimation of an interior permanentmagnet motor from initial states”, IEEE Transactions on Industry Applications, 39(3), p761-767, (2003).
• L. I. Iepure, I. Boldea, G. D. Andreescu, and F. Blaabjerg, “Improved state observers for sensorless single phase BLDC-PM motor drives”, IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, p870-875, (2010). [https://doi.org/10.1109/iecon.2010.5675170]
• S. Bentouati, Z. Q. Zhu, and D. Howe, “Influence of design parameters on the starting torque of a single-phase PM brushless DC motor”, IEEE Transactions on Magnetics, 36(5), p3533-3536, (2000). [https://doi.org/10.1109/20.908890]
• H. B. Ertan, B. Dag, and G. Capolino, “Calculation of some parameters of single phase PM motor for design optimization”, IEEE Transactions on Energy Conversion, 2(3), p538-548, (2005).
• K. W. Lee, “The sensorless control technology based on model of permanent magnet synchronous motor”, The Transaction of the Korean Institute of Power Electronics, 21(3), p27-33, (2016), (in Korea).
• J. I. Ha, and S. H. Jung, “The sensorless control technology based on signal injection of PMSM”, The Transaction of the Korean Institute of Power Electronics, 21(3), p34-41, (2016), (in Korean).
• L. I. Iepure, I. Boldea, and F. Blaabjerg, “Hybrid I-f starting and observer-based sensorless control of single-phase BLDC-PM motor drives”, IEEE Transactions on Industrial Electronics, 59(9), p3436-3444, (2012). [https://doi.org/10.1109/tie.2011.2172176]
• U. S. Seong, and S. H. Hwang, “Analysis of phase error effects between virtual two-phase voltages in SRF-PLL based on APF”, International Conference on Power Electronics-ECCE Asia, p2215-2220, (2015). [https://doi.org/10.1109/icpe.2015.7168084]
• S. H. Kim, Hysteresis Regulator, DC, AC, BLDC motor control, Korea, Bogdoo Pulishing Company, (2014), (in Korean).
• S. G. Sul, Contoller Design, Electrical Equipment Control Theory, Korea, Hongrung Publishing Company, (2012), (in Korean).