터그보트와 바지선의 예인 간격에 관한 저항성능 수치 시뮬레이션
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문에서는 터그보트와 예인되는 바지선의 간격에 따른 저항성능 변화에 대한 연구를 수행하였다. 저항성능 평가를 위해 상용 점성유동 프로그램인 Star-CCM+를 이용하여 간격이 서로 다른 4가지 경우에 대한 수치 시뮬레이션을 수행하였다. 또한 한국선급의 부선예항검사규칙에서 제안하고 있는 바지선의 저항 계산 방법과 비교를 수행하였다. 수치 시뮬레이션 결과, 예인선과 바지선의 간격이 터그보트 길이의 3배까지는 바지선의 저항이 감소하는 경향을 보임을 확인할 수 있었다. 경험식과 수치 시뮬레이션 결과를 비교 시, 수치 시뮬레이션이 경험식보다 약 40% 작게 저항성능을 추정하고 있다.
Abstract
This study evaluates resistance performance based on the gap between a tugboat and a towed barge. For the evaluation of the resistance performance, numerical simulations are performed for 4 cases with different gaps using Star-CCM+, which is a commercial viscous flow S/W. In addition, the results of the numerical simulation are compared with the empirical formula proposed in the rule of the KR(Korean Resister) towing survey of barges and tugboats. In the numerical simulation results, the resistance of the barge tended to decrease until the gap between the tugboat and barge was three times the tugboat length. The comparison between the numerical simulation and empirical formula shows that the numerical simulation estimates the resistance performance as approximately 40% smaller.
Keywords:
Tugboat, Towing, Barge, Resistance performance, Numerical simulation키워드:
터그보트, 예인, 바지선, 저항성능, 수치 시뮬레이션1. 서 론
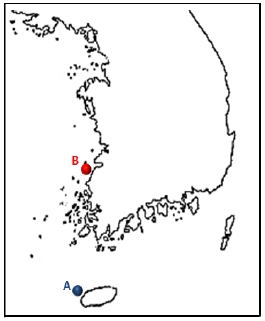
국내에서는 Figure 1과 같이 제주도(A)에 30MW 규모의 탐라해상풍력단지가 조성되어 운영 중에 있으며, 서남해(B)에 60MW 규모의 해상풍력단지가 조성 중에 있다.
해상풍력단지를 조성하기 위해서는 해상풍력발전기 설치선이 필수적이며, 국내에는 전용 설치선의 부재로 갑판 승강식 구조물(Self Elevated platform)인 잭업(Jack up) 바지선을 이용하여 해상풍력발전기를 설치하고 있다. 전용 설치선을 이용하는 방법과 잭업 바지선을 이용하는 방법은 각각의 장단점이 있으며, 이에 대한 연구로 D. Ahn et al. [1]은 국내 서남해 해상을 대상으로 다양한 외부 환경 요인들을 고려하여 각각의 해상풍력발전기 설치 방법을 비교 분석하였다.
잭업 바지선을 이용한 해상풍력발전기 설치의 경우 잭업 바지선은 설치 지역에 잭업 후 대기하고, 별도의 운반용 바지선이 운용되어 해상풍력발전기를 운반한다. 이 때, 운반용 바지선은 통상적으로 무동력 바지선이 이용되며 터그보트에 의해 설치 지역으로 예인된다.
예인되는 바지선의 저항을 추정하기 위해 한국선급은 부선예항검사 규칙에서 바지선의 저항 추정 방법을 제시하고 있으며[2], E. C. Kim et al. [3]은 바지선에 작용하는 저항 성능 추정 방법에 대한 연구로 기존의 저항 추정 방법을 분석 및 새로운 방법을 제시하였다. 또한 바지선의 적재상태에 따라 수선 상부에 작용하는 풍하중 영향을 파악하기 위해 J. Seok et al. [4]은 수치 해석적 방법을 이용하여 연구를 수행하였으며, E. C. Kim and H. J. Choi [5]는 사고선박의 예인력 산출을 위한 공기저항 추정 방법에 대한 연구를 수행하였다.
바지선을 예인하는 터그보트의 경우 바지선의 적재상태에 의한 저항 및 외부 환경 조건에 따른 외력을 이겨낼 정도로 충분한 추력이 요구되며, 경제적인 터그보트 선정을 위해 예인되는 바지선의 저항성능 파악이 필수적이라 할 수 있다.
따라서 본 논문에서는 운반용 바지선의 저항 추정에 관한 연구의 일환으로 수치 해석적 방법을 이용하여 예인용 터그보트와 바지선의 예인 간격에 따른 저항성능 변화에 대한 연구를 수행하였다.
2. 저항성능 추정 방법
2.1 부선 예항 기준
예인되는 바지선에 작용하는 전체저항은 식 (1)과 같으며, 각각의 저항성분은 식 (2) ~ 식 (4)와 같다[2].
| (1) |
이 때 Rt는 전체저항, Rf는 마찰저항, Rw는 조파저항, Ra는 공기저항이다.
| (2) |
마찰저항은 식 (2)와 같이 선체표면의 상태(Ff), 침수표면적(Af) 그리고 예인속력(V)의 함수이다.
| (3) |
조파저항은 식 (3)과 같이 거친 해상상태 저항계수(Cw), 바지선 선수형상 계수(Fw), 수선하부선체 횡단면적(Aw)과 예인속력의 함수이다.
| (4) |
공기저항은 식 (4)와 같이 바람에 면한 선체표면의 형상계수(Ca), 바람에 면한 면적중심의 수면으로부터 높이(Da), 수선상부의 횡단면적(Aa), 항해구역에 따른 풍속(Va)과 예인속력의 함수이다.
또한 파(Wave)로 인해 발생하는 부가저항의 경우, 유효파고에 따라 1~16 ton 의 부가저항을 추가로 고려해야 한다[2].
2.2 모형선-실선 저항 추정법(ITTC-1957)
선박의 저항 추정을 위한 방법으로 실험적 방법, 수치 해석적 방법 그리고 통계적 방법 등 다양한 방법이 있다. 가장 대표적인 방법인 모형선 실험을 통한 실선의 저항을 추정하는 방법의 경우, 국제수조협회(International Towing Tank Conference, ITTC)에서 제시한 ITTC-1957, ITTC-1978 방법 등이 있다.
대표적인 ITTC-1957 방법의 경우 식 (5), 식 (6)과 같이 전체저항을 마찰저항과 잉여저항으로 분리하고, 마찰저항은 레이놀드 수의 함수로 식 (7)과 같이 계산된다.
| (5) |
| (6) |
| (7) |
이 때, CT는 전체저항계수, CF는 마찰저항계수, CR은 잉여저항계수로 밀도와 속력 그리고 침수표면적을 이용하여 무차원 된 계수이며, CA는 모형선-실선 보정 계수, 하첨자 m과 s는 각각 모형선과 실선을 나타내며, Rn은 레이놀드 수이다.
다만 본 연구에서는 수선 상부 형상을 포함하여 수치 시뮬레이션을 수행함에 따라 바람의 저항을 포함하고 있는 CA를 그대로 적용하기는 적합하지 않다. 따라서 CA는 식 (8) ~ 식 (10)과 같이 수정하여 사용하였으며[6] 바람에 의한 저항은 별도로 보정하지 않았다.
| (8) |
| (9) |
| (10) |
이 때, LBP (Length bet. perpendiculars)는 수선간 길이이다.
3. 선박 및 수치 시뮬레이션
3.1 대상 선박
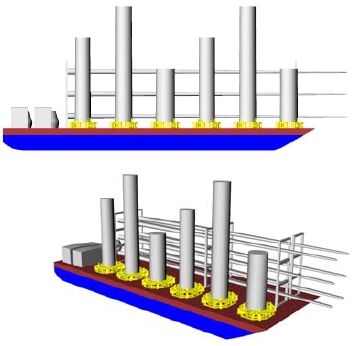
본 연구에 사용된 선박은 Figure 2, Figure 3과 같이 28m급 터그보트와 76m급 바지선으로 각각의 상세 제원은Table 1, Table 2와 같다.
수치 시뮬레이션 시 격자수에 따른 해석 시간 증가를 피하기 위해 해상풍력발전기 타워 하부에 위치한구조물인 가이드 프레임의 경우 복잡한 형상을 사각형상으로 단순화하여 해석을 수행하였다.
3.2 수치 시뮬레이션 방법
본 연구에 이용된 지배방정식은 연속 방정식과 RANS (Reynold-averaged Navier-Stokes) 방정식으로 식 (11), 식 (12)와 같으며 비정상, 비압축성 및 점성 유동을 가정하였다.
| (11) |
| (12) |
여기서 U는 평균속도벡터, x는 좌표계, t는 시간, p는 압력, μ는 점성계수, B는 체적력, 는 난류전단응력으로 난류모델에 의해 결정되며, 본 논문에서는 Standard k-ϵ 모델을 개량한 Realizable k-ϵ 모델을 적용하였다[7].
상술한 지배방정식은 유한체적법(Finite-volume method, FVM)에 의해 이산화되며, SIMPLE(Semi-implicit method for pressure linked equations) 알고리즘으로 압력과 속도의 연성을 고려하였다.
3.3 격자계
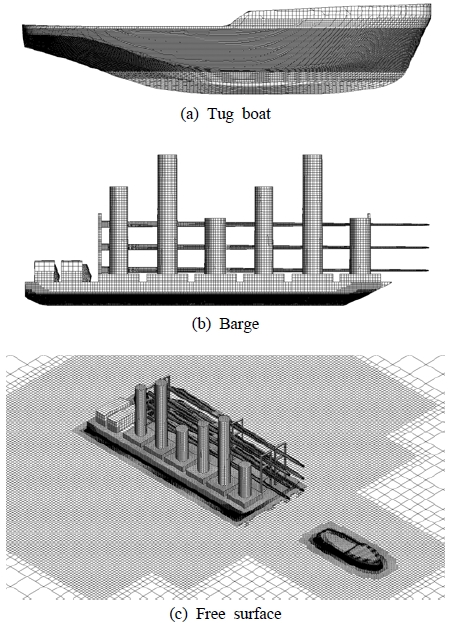
격자계의 경우 Star-CCM+에서 제공하는 자동격자생성 방법인 Surface remesher와 Trimmer 방법을 이용하여 Figure 4와 같이 격자를 생성하였다. 터그보트와 바지선은 선체 주위의 점성 유동을 고려하기 위해 Prism layer 방법을 이용하여 각각의 선체 법선 방향으로 5개의 Layer를 추가로 배치하여 Y+가 100 이하가 되도록 설정하였다. 이 때, 수치 시뮬레이션에 이용된 총 격자수는 약 500만개이다.
3.4 수치 시뮬레이션 조건
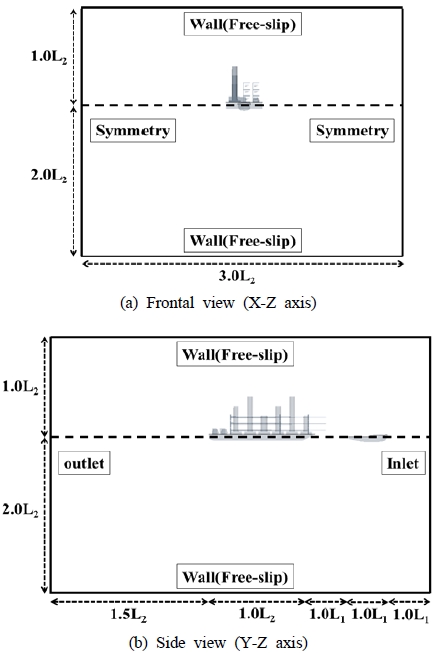
수치 시뮬레이션을 위한 계산영역은 Figure 5와 같이 길이방향 3.0L1+2.5L2, 폭방향 3.0L2 그리고 높이방향 3.0L2 이다. 이 때, L1은 터그보트의 전장이며 L2는 바지선의 전장이다.
경계조건의 경우 상부와 바닥은 벽(Wall-Free slip) 조건, 양옆은 대칭(Symmetry) 조건을 설정하였다. 선박(터그보트, 바지선)의 경우 점성유동을 고려하기 위해 벽(Wall-No slip) 조건을 설정하였다. 또한 선박(터그보트, 바지선)의 속도의 경우 유동이 유입되는 입구에는 유입(Inlet) 조건, 반대편 유동이 유출되는 출구는 유출(Outlet) 조건을 설정하여 유동의 유출입으로 고려하였다.
공기와 물의 자유표면은 VOF(Volume-of-fluid) 방법을 이용하여 고려하였으며, 선박(터그보트, 바지선)의 선속이 5 knots의 저속인 점을 감안하여 상하동요 및 종동요는 고려하지 않았다.
터그보트와 바지선의 간격의 경우 1L1, 2L1, 3L1 그리고 4L1의 4가지 경우에 대한 수치 시뮬레이션을 수행하여 예인 시 간격에 따른 저항성능의 변화를 파악해 보았다.
4. 수치 시뮬레이션 결과
터그보트와 운반용 바지선의 간격에 따른 수치 시뮬레이션 결과는 Table 3과 같다.
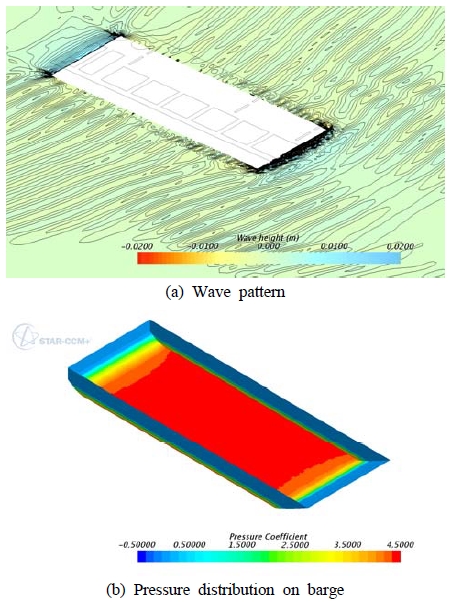
모형선을 이용한 수치 해석 결과, 터그보트와 바지선의 간격이 1L1에서 4L1까지 거리가 증가할수록 바지선에 작용하는 저항이 감소하고 있다. 다만, 3L1까지는 거리가 증가할수록 저항 감소량이 증가하는 경향을 보이지만, 4L1에서는 저항 감소량이 3L1 대비 1% 미만으로 감소하고 있다. 이는 터그보트의 인해 발생하는 후류의 영향이 3L1 이상에서는 점차 감소하기 때문이다. 또한 이로 인해 터그보트와 바지선의 간격이 4L1 이상 증가하더라도 저항 감소량은 미비할 것으로 사료된다. 이 때, 3L의 파형 및 바지선의 압력 저항 분포는 Figure 6과 같다.
실선의 유효 마력 추정을 위해 2.2절에서 제안한 식 (5) - 식 (9)를 이용하여 Table 3과 같이 실선의 유효 마력을 추정하였다. 이 때, 식 (10)의 ks는 경우 신조선 표면 거칠기 값으로 사용되는 150μm를 적용하였으며, S.M(Sea Margin)은 15%로 고려하였다.
터그보트와 바지선의 간격에 따라 유효마력은 약 101~107kW로 추정되며 1L1을 기준으로 2L1은 약 2%, 3L1은 약 5% 그리고 4L1은 약 6% 저항 감소율을 보인다. 이 때 바람에 의해 상부 구조물에 작용하는 저항이 전체저항의 약 3%를 차지하며, 선체 하부에 작용하는 저항은 전체저항의 약 97%를 차지한다. 선체하부의 작용하는 저항의 경우 마찰저항과 잉여저항으로 구분할 수 있으며, 이 때 마찰저항은 레이놀드 수가 동일하기 때문에 변화가 없으며, 잉여저항은 거리에 따라 45%~50% 범위로 거리가 증가할수록 감소하고 있다.
2.1절에서 전술한 경험식 방법을 이용한 저항 성능 추정을 위해 Table 4의 계수들을 적용하였다[2]. 단, 이 때 Va의 경우 바지선이 운용되는 지역에 따라 평수구역은 29.16knots, 연해구역은 36.93knots 그리고 근해구역은 50.54knots로 고려해야 하지만 본 연구에서는 수치 시뮬레이션과 비교를 위해 0으로 두었다.
계산 결과 Table 5와 같이 바지선의 총 저항은 약 149kW로 추정된다. 이 때 각각의 저항 성분의 비율은 마찰저항이 전체의 92%로 대부분을 차지하고 있으며, 조파저항이 약 3% 그리고 바람에 의한 저항이 약 5%이다.
예인삭의 길이 계산 방법인 식 (13)을 이용하여 예인삭의 길이를 계산하면 207.8m이다. 이는 터그보트와 바지선의 최대 간격으로 고려할 수 있다.
| (13) |
이 때, S는 예인삭의 길이, K는 항해구역에 따른 계수로 1을 적용하였다[2].
수치 시뮬레이션이 수행된 최대 길이는 4L1로, 예인삭의 길이는 약 110m에 해당한다. 하지만 전술하였듯이 3L1과 4L1의 전체 저항 변화율이 1% 미만으로 점차 수렴하는 경향을 보인다. 따라서 터그보트와 바지선의 간격이 200m 이상으로 길어지더라도 전체 저항의 변화는 미미할 것으로 사료된다. 따라서 수치 시뮬레이션 결과와 경험식 결과의 비교 시 수치 시뮬레이션은 4L1의 결과를 이용하였다.
수치 시뮬레이션 결과와 경험식의 계산 결과는 총 저항이 약 40% 정도 차이나고 있으며, 경험식이 전체저항을 상대적으로 과도하게 추정하고 있다. 이 때 각각의 저항성분은 마찰저항이 약 90% 과도하게, 조파저항이 약 60% 과소하게 추정하고 있으며 바람에 의한 저항은 상대적으로 유사한 결과를 보이고 있다.
5. 결 론
본 연구에서는 해상 운반에 많이 이용되고 있는 터그보트와 바지선에 대한 연구로 예인 시 예인 간격에 따른 저항성능 변화에 대한 연구를 수행하였다.
예인 간격에 따른 저항성능 변화를 추정하기 위해 수치 해석적 방법을 이용하여 4가지 예인 간격에 대한 해석을 수행하였다. 또한 그 결과를 비교하기 위해 한국선급에서 제안하고 있는 경험식을 통한 저항추정을 수행하였으며, 그 결과는 아래와 같다.
(1) 수치 시뮬레이션 방법
모형선의 저항을 계산하여 실선의 저항을 추정하는 방법을 이용하였으며, 실선으로의 확장은 ITTC-1957 방법을 이용하였다. 이 때, 모형선-실선 상관 계수의 경우 상부 구조물을 포함하여 수치 시뮬레이션을 수행했기 때문에 ITTC-1957 방법에서 제안하는 계수(CA)를 대신하여 거칠기 보정 계수(CΔf)와실선 확장 계수(CA′)를 적용하였다.
계산 결과 터그보트와 바지선의 간격이 증가할수록 바지선에 작용하는 저항이 감소하고 있으며, 3L1 이상에서는 저항 증가율이 감소하였다. 따라서 저항 성능 측면에서 예인 시 터그보트와 바지선의 간격을 고려한다면 3L1이 가장 좋을 것으로 사료된다.
(2) 경험식 방법
한국선급에서 제안하고 있는 부선예항검사 규정에 맞춰 바지선의 저항성능을 추정한 결과 약 149kW로 수치해석을 통해 계산된 결과보다 약 40% 과도하게 바지선의 저항을 추정하고 있다.
이는 수치 시뮬레이션이 정수 중에서 계산되어, 경험식에서 적용하고 있는 거친 해상상태(Cw)로 인해 발생하는 부가저항을 반영하지 못해 발생하는 차이로 사료된다.
이 때, 바지선에 작용하는 각각의 저항성분 중 마찰저항이 약 92%로 대부분을 차지하고 있다. 이는 경험식에서는 전체저항을 마찰저항과 조파저항 그리고 바람에 의한 저항으로 구분하고 있지만, 마찰저항에 압력형상저항이 포함되어 있을 것으로 사료된다.
다만, 본 연구의 수치 시뮬레이션에는 터그보트의 추진기가 고려되지 않아 터그보트로 인해 발생하는 후류의 영향을 전부 고려하지 못하였다. 또한 예인 시 발생할 수 있는 바지선과 예인선의 동요로 인한 불안정성이 고려되지 않았다. 따라서 추후 터그보트의 추진기를 고려한 추가적인 연구 및 선박 운동을 고려한 해석이 추가적으로 수행될 필요가 있다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다. (No. 20153030024010) 그리고 또한, 본 연구는 해양수산부(MOF)와 해양수산과학기술진흥원(KIMST)의 지원을 받아 수행한 연구 과제입니다. (No. 201601572)
References
-
D. Ahn, S. C. Shin, S. Y. Kim, H. Kharoufi, and H. C. Kim, “Comparative evaluation of different offshore wind turbine installation vessels for Korean west–south wind farm”, International Journal of Naval Architecture and Ocean Engineering, 9(1), p45-54, (2017).
[https://doi.org/10.1016/j.ijnaoe.2016.07.004]

- Rules for the Towing Survey of Barges and Tugboats, Korean Resister, Busan, Korea, (2014).
-
E. C. Kim, H. J. Choi, and S. G. Lee, “A study on the hull resistance prediction methods of barge ship for towing force calculation of disabled ships”, Journal of the Korean Society for Marine Environment &Energy, 16(3), p211-216, (2013), (in Korean).
[https://doi.org/10.7846/jkosmee.2013.16.3.211]

-
J. Seok, S. Y. Kim, J. C. Park, and T. H. Cha, “Arrangement of guide frame for offshore wind turbine considering wind load”, Journal of Korean Society of Marine Engineering, 41(9), p836-840, (2017), (in Korean).
[https://doi.org/10.5916/jkosme.2017.41.9.836]

-
E. C. Kim, and H. J. Choi, “A study on the simplified prediction method of air resistance for towing force calculation of disabled ships”, Journal of the Korean Society for Marine Environment & Energy, 17(3), p198-204, (2014), (in Korean).
[https://doi.org/10.7846/jkosmee.2014.17.3.198]

- ITTC Recommended Procedures and Guidelines, “1978 ITTC Performance Prediction Method”, ITTC, 7.5-0203-01.4, (2011).
-
T. H. Shih, W. W. Liou, A. Shabbir, Z. Yang, and J. Zhu, “A NEW kt EDDY VISCOSITY MODEL FOR HIGH REYNOLDS NUMBER TURBULENT FLOWS”, Computers Fluids, 24(3), p227-238, (1995).
[https://doi.org/10.1016/0045-7930(94)00032-t]