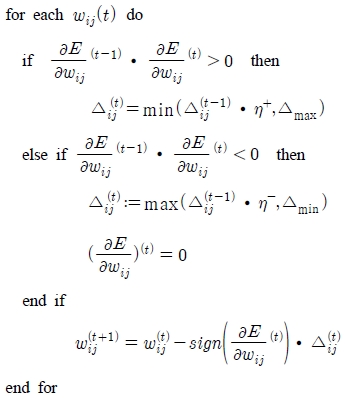플럭스코어드와이어의 용접특성 예측을 위한 탄력적 오류역전파 신경망 모델에 관한 연구

1. 서 론

선박이나 해양플랜트 건조 시에 널리 활용되는 용접재료인 플럭스 코어드 와이어(Flux Cored Wire, 이하 FCW)는 플럭스 코어드 아크 용접(Flux-Cored Arc Welding, 이하 FCAW)용 용접재료로서 튜브형의 와이어에 플럭스가 채워진 형태를 취하고 있다. FCW는 모재의 종류에 따라 다양하게 분류되며 사용 모재나 용접 시 요구되는 성능에 적합한 특성을 지닌 종류가 사용된다. FCW의 요구특성은 작업성과 용착금속성분, 기계적 성질 및 기타특성 등으로 60항목 이상이지만 통상 그 중 중요한 10~30항목의 특성으로 이루어진다. FCW의 특성은 와이어 성분보다는 주로 와이어에 채워진 플럭스의 구성성분에 의해 좌우된다. 즉, FCW의 설계의 핵심은 플럭스 원재료의 종류와 배합량을 결정하는 데에 있다. 현재 사용되는 플럭스의 원재료는 150가지 내외인데 한 FCW는 20~40가지의 플럭스 원재료를 적절한 비율로 함유한다. 따라서 특정한 한 FCW를 개발하는 것은 150종의 원재료 중 20~40종의 원재료를 선택하고 각각의 배합량을 결정하는 문제로 귀결되며 이 경우 가능한 조합은 수만 가지에 이르게 된다. 이 문제는 수십 종의 플럭스 성분과 각각의 배합량에 의해 10~30항목의 요구특성이 정해지는 고도의 비선형문제에 해당된다. 각각의 플럭스 원재료가 용접특성에 미치는 영향은 대략적인 정성적 상관관계만 알려져 있을 뿐, 정량적으로 명확히 밝혀진 바가 없다. 현재까지 특정 요구특성을 갖는 FCW의 개발은 용접재료 설계자들의 지식과 경험에 전적으로 의존해 많은 시행착오를 거쳐 수행되어 왔다[1][2].

인공신경망(Artificial Neural Network, 이하 ANN)은 상호 영향을 미치는 인자가 많고 복잡한 상관관계를 갖는 문제를 해결하는데 우수한 기능을 갖고 있는 기법이다. 특히 실험적인 데이터가 충분히 확보되어 있음에도 고도의 비선형성으로 인해 수학적인 규명이 어렵고 통계적인 분석도 난해한 문제의 경우 ANN은 특유의 학습능력을 통해 이를 해결하는 탁월한 성능을 보여 다양한 분야에서 적용을 확대하고 있다[3][4]. ANN은 난해한 문제 해결에 강점을 가지고 있지만 다량의 데이터가 확보되어야 한다는 점과 학습과정에서 긴 계산 시간을 필요로 하는 점이 제한요소가 되어왔다. 이 중 긴 학습 시간이 소요되는 문제는 탄력적 오류역전파 학습 알고리즘이나 확률통계기법을 접목한 딥러닝 알고리즘을 통해 획기적으로 개선되어 적용 범위를 넓히고 있다. ANN은 용접분야에서도 용접조건 최적화와 용접신호처리 분야 등에서 많이 활용되어 왔다[5]-[7]. 본 연구에서는 ANN을 적용하여 다양한 플럭스 원재료의 조합에 대한 용접특성을 예측하여 요구되는 용접특성을 만족할 수 있는 플럭스의 적절한 조합을 구하고, 이에 대해 시제품을 만들고 성능시험을 수행함으로써 FCW의 개발에 소요되는 시간과 비용을 줄이는 것을 목표로 하였다. 이를 위해 본 연구에서는 기존의 ANN보다 학습효과가 뛰어나고 병렬처리계산에 의해 학습시간을 현저히 줄인 탄력적 오류역전파 신경망을 FCW 설계에 적용하여 다양한 플럭스 성분 조합에 대한 용접특성을 예측하는 ANN 모델을 구축하였고 검증데이터를 이용하여 이 모델에 대한 검증을 수행하였다.

2. FCW 데이터의 특성 및 설계 과정

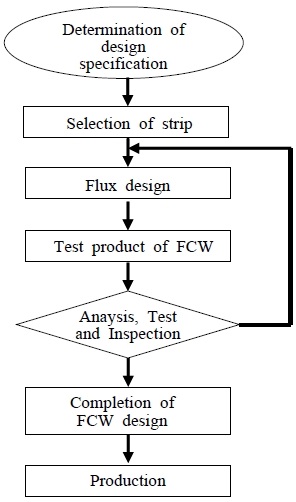
FCW는 튜브형 와이어 내부에 플럭스가 채워진 형태로 내부 플럭스의 조합이 FCW의 특성을 결정하며 용접 결과에 중대한 영향을 준다. 튜브형 와이어는 스트립(strip)을 둥글게 말아서 만드는데 스트립의 종류와 성분에 따라 용접특성에 영향을 주지만 제선과정을 통해 대량으로 생산되는 제조특성 상 다양한 종류로 만들어지지 않기 때문에 플럭스 조합이나 배합율과 같이 임의로 조정될 수 없으므로 용접특성에 변화를 주는 요인이 제한적이다. 따라서 FCW의 설계 과정은 FCW가 요구되는 특성을 가질 수 있도록 우선 스트립을 선택하고 튜브형 와이어 속에 채워질 다양한 플럭스의 종류와 배합율을 결정하는 과정이라고 볼 수 있으며 이 때 플럭스 종류 및 배합율의 결정을 플럭스 설계(Flux design)라고 한다. 스트립과 플럭스 설계의 초안이 정해지면 초안대로 시험용 FCW를 제작하고 제작된 FCW로 용접을 시행한 후 용접과정 및 용접결과에 대한 시험∙검사를 통해 설계 목표, 즉 설정된 용접 특성치를 만족하는지 확인을 한다. 이 과정에서 설계 목표에서 미달하는 경우 다시 플럭스 설계 과정을 거쳐 새로운 시험용 FCW의 제작과 시험∙검사를 시행하며 이 과정은 설계 목표와 부합하는 결과가 나올 때까지 반복된다. Figure 1은 이 과정을 보여주는 흐름도이며 이 일련의 과정에 많은 시간과 비용이 소요된다.

Figure 1:

Flow chart of FCW Design

FCW 용접특성치는 육안검사가 주된 검사인 대략 10개 항목의 작업성과 용착금속의 화학성분 25항목, 인장강도, 충격치 등의 기계적 특성치 25항목 등 60항목 내외인데 FCW의 용도에 따라 이 중 20~30항목이 조사된다. 이 특성치들은 육안에 의존하거나 검사장비에 따라 검사값에 상당한 차이가 존재한다. 아크용접은 재현성이 좋지 않은 용접공정으로 동일한 조건의 용접에서도 일정범위 이내이긴 하나 용접결과는 상이한 경우가 많다. 따라서 FCW의 설계 및 용접특성치 관련 문제를 다루는 경우 이러한 오차를 감안하여 해결책을 마련하여야 한다.

3. 탄력적 오류역전파 신경망

3.1 탄력적 오류역전파 알고리즘

많은 비선형 상관관계 문제 해결에 적용되는 기존의 ANN은 입력층과 은닉층 및 출력층으로 구성된 3층 신경망으로 일반화된 델타 규칙(General Delta Rule. 이하 GDR)을 학습규칙으로 사용한다. GDR은 대표적인 오류 역전파 알고리즘으로 목표치와 신경망의 출력치의 차이인 오차 E 를 줄여나가는 방법으로 경사하강법을 사용한다. 경사하강법은 신경망의 각 노드를 연결하는 값인 연결가중치 w_ij를 변화시킬 때 전체 오차가 줄어드는 방향으로 값을 변화시키는 방법으로 연결가중치의 변화량인 식 (1)과 현재의 스텝에서 수정된 연결가중치인 식 (2)로 표현된다. GDR은 오차값을 출력층에서 계산한 후 이를 역방향으로 은닉층과 입력층으로 전파시켜 연결가중치를 변경시키므로 오류역전파 알고리즘으로 부르며 학습과정은 GDR을 통해 연결가중치를 변화시켜 전체 오차를 허용한계오차 내에 도달할 때까지 반복하는 과정이다.

$\[ \mathrm{\Delta }{w}_{ij}=-\eta \cdot {\left(\frac{\partial E}{\partial w_{ij}}\right)}^{\left(t\right)} \]$

(1)

식 (1)에서 η는 학습율, E는 오차의 총합, $$ {\left(\frac{\partial E}{\partial w_{ij}}\right)}^{\left(t\right)}$$는 노드 i와 j간의 연결가중치에 대한 총오차의 변화율을 뜻한다.

$\[ w_{ij}\left(t+1\right)=w_{ij}\left(t\right)+\text{Δ}{w}_{ij} \]$

(2)

식 (2)에서 w_ij(t+1)는 스텝 t에서 수정된 연결가중치, w_ij(t)는 스텝 t 상태의 연결가중치를 뜻한다. 이 방법은 거의 모든 비선형 상관관계 문제에 적용될 수 있지만 문제의 특성과 신경망의 층수와 각 층의 노드 수 및 학습데이터의 양에 따라 오차의 수렴속도와 수렴값에 큰 차이를 나타낸다. 이 현상은 많은 경우 연결가중치의 변화를 학습율과 현 단계의 오차변화율에만 의존하고 있는 것에 기인한다. 연결가중치의 변화가 큰 경우는 오차의 극소치 부근에서 진동현상을 보여 오차의 수렴을 어렵게 만들며 작은 경우는 수렴하기까지 더 많은 반복계산을 필요로 한다. 한계오차값 내로 수렴하는데 소요되는 반복계산 횟수는 신경망 모델의 층수, 각 층의 노드 수 등에 따라 차이가 있지만 작게는 수십만회에서 많게는 수천만회에 이른다.

탄력적 오류역전파 알고리즘(Resilient Back-Propagation, 이하 Rprop)은 기존의 GDR의 학습규칙과 같이 총오차를 감소시키는 방향으로 연결가중치를 변화시키는 오류 역전파 알고리즘에 속하지만 연결가중치의 변화를 현 단계의 오차변화율과 함께 그 전 단계의 오차변화율도 고려하는 점에서 차이가 있다. 즉, 현 단계의 오차변화율과 전 단계의 오차변화율의 부호가 같은 경우는 계속 오차가 감소하는 과정이므로 연결가중치의 변화량을 크게 늘리고 부호가 다른 경우는 전 단계와 현 단계사이에 극소값이 존재한다는 의미이므로 연결가중치의 변화량을 줄임으로써 오차의 수렴속도를 증가시키고 오차의 수렴값도 낮출 수 있다[8][9].

Rprop에서는 스텝변화량(step-size) $$ {\text{Δ}}_{ij}^{\left(t\right)}$$를 도입하여 이 값이 현 단계의 오차변화율과 전 단계의 오차변화율의 곱의 부호에 따라 식 (3)과 같이 정의한 후 이 값을 이용하여 실제 연결가중치의 변화량을 각각의 경우에 대해 구한다. 실제 연결가중치의 변화량을 구하는 방식은 가중치의 역추적(Weight-backtracking)을 허용하는 방식과 허용하지 않는 방식에 따라, Rprop+, Rprop-, iRprop+, iRprop- 의 4가지가 있으나 그 중 많은 경우 효율적인 방식으로 인정되는 iProp- 방식을 본 논문에서는 채택하였다[10]. iProp- 알고리즘은 Figure 2로 표현된다.

(3)

Figure 2:

iProp- Algorithm

Figure 2에서 전·현단계의 오차변화율 곱이 양수값인 경우 변화량 $$ {\text{Δ}}_{ij}^{\left(t\right)}$$ 는 전단계의 변화량에 더 높은 학습율 η⁺를 곱한 값과 발산되는 경우를 대비해 미리 설정해 둔 최대 변화량 중 적은 값을 택하여 전체적으로 변화량을 증가시킨다. 한편 곱이 음수값인 경우는 전단계의 변화량에 더 낮은 학습율 η^-를 곱한 값이나 또는 0으로 급격히 수렴되는 경우를 대비해 미리 설정해 둔 최소 변화량 중 큰 값을 택하여 변화량을 감소시킴과 함께 $$ {\left(\frac{\partial E}{\partial w_{ij}}\right)}^{\left(t\right)}=0$$으로 두어 다음 단계에서 이전 단계의 학습율을 그대로 사용하게 하여 한번에 감소효과가 배증되는 것을 피한다. 학습과정은 통상 수만번에서 수백만번의 계산이 반복되어 효과가 누적되므로 오차의 수렴속도는 수십배에서 수백배로 증가되며 오차의 수렴값도 극소값 부근에서 미세하게 조정되므로 충분히 낮은 값을 얻을 수 있다.

3.2 FCW 용접특성 예측을 위한 탄력적 오류역전파 신경망 모델

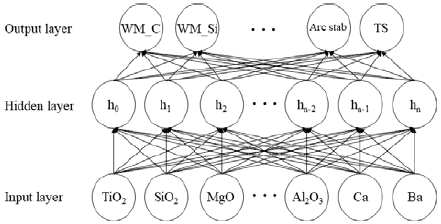
본 연구에서는 FCW용 플럭스의 원재료 종류 및 배합량이 주어질 때 튜브형 와이어와 각각의 플럭스 원재료를 구성하는 화학성분을 추출하여 한 FCW에 포함된 전체의 화학성분의 종류 및 각 성분의 구성비가 주어질 때 용접특성치를 예측하는 ANN 모델을 구현하고자 하였다. 신경망 모델을 학습하기 위해 사용된 학습 및 검증용 데이터는 용접와이어 제조사로부터 제공받아 사용하였다. 신경망 모델은 수집된 FCW 데이터를 유형별로 구분하여 5개의 모델을 생성하였다. 5개의 모델은 모두 Figure 3과 같이 입력층, 은닉층, 출력층으로 구성된 3 층(layer) ANN 모델이며 각 층의 노드(또는 뉴런)수는 모델 종류에 따라 다르다. 각 신경망 모델의 입력층 노드 수와 이에 대응되는 입력데이터의 항목과 출력층 노드 수 및 이에 대응되는 출력데이터의 항목은 Table 1과 같다. 입력층과 출력층의 노드수는 입력데이터와 용접특성치의 항목수에 의해 결정되지만 은닉층의 노드수는 모델의 설계에 따라 달라진다. 은닉층의 노드수를 증가시키면 문제해에 대한 자유도가 높아져 오차의 수렴이 용이한 경향을 보이지만 과적화(overfitting)의 경향을 보이는 걸로 알려져 있다. 과적화는 ANN의 난제 중의 하나로서 학습데이터에 대한 오차는 적지만 학습되지 않는 데이터에 대한 오차가 큰 현상을 의미하며 모델의 유효성을 저하시키는 요인이다[11]. 은닉층의 노드수를 결정하는 특별한 규칙은 아직까지 알려진 바가 없고 대상 문제에 따라 다르게 적용된다. 본 논문에서는 은닉층 노드수를 입력층 노드수와 같은 값과 입력층 노드수와 출력층 노드수의 중간값을 적용하였다.

Figure 3:

Structure of ANN model

Table 1:

Detailed information about 5 ANN model

이상적인 ANN 모델은 넓은 범위에 적용가능하면서도 많은 항목의 특성을 예측할 수 있는 것이 바람직하지만 데이터가 다양하면 영향인자들도 많고 그들 사이의 상관관계도 복잡해지므로 학습시간이 기하급수적으로 길어지며 학습오차가 커지고 예측치의 정확도도 떨어진다. 한편 ANN모델에 사용되는 학습데이터의 양이 적으면 반복계산횟수를 늘려 학습오차를 줄여도 과적화 현상에 의해 학습되지않은 데이터에 대한 예측치의 정확도는 떨어진다.

본 연구에서는 데이터의 유사성 및 양과 출력항목의 다소에 따라 예측 정확성, 즉 모델의 유효성의 경향을 파악하여 바람직한 모델을 제시할 수 있도록 5개의 ANN 모델을 설계하였다. Model 1~3은 각각 스테인리스강용, 탄소강 중 전자세용접용, 탄소강 중 저온강용의 비교적 좁은 범위에 적용 가능한 FCW 데이터로 구성되어 있어 데이터의 유사성이 큰 만큼 데이터의 양이 적고 예측 가능한 출력항목은 많다. Model 4는 모든 탄소강, Model 5는 전체 탄소강 및 스테인리스강에 적용되는 FCW 데이터로 구성되어 데이터의 양은 많지만 데이터의 유사성이 낮고 그만큼 공통적 출력항목이 적다. Table 1은 각 모델에 대한 입력과 출력 항목에 대한 상세내용이 제시되어 있다. 각 모델을 위해 확보된 데이터는 75%를 학습용으로 사용하고 학습된 ANN 모델의 유효성을 검증하는 검증용 데이터로 나머지 25%를 사용하였다.

4. 학습 결과 및 검토

학습은 ANN의 핵심 기능으로 주어진 입력데이터와 출력데이터에 학습알고리즘을 적용시켜 그들 간의 상관관계를 수립하는 과정이다. 학습데이터가 유사한 특성을 가진다면 학습데이터의 입력데이터와 출력데이터의 상관관계가 수백차원의 비선형 관계를 갖는 복잡성을 가지더라도 ANN은 입력항목과 출력항목 사이의 상관관계를 수립할 수 있다.

FCW 설계과정은 30여종의 플럭스 화학구성물과 10~20여종의 용접특성항목과의 상관관계를 파악해야하는 고도의 비선형 문제로서 이 문제의 해를 구할 수 있는 법칙이나 방정식이 존재하지 않는다. 따라서 많은 경험과 용접야금학적인 지식을 갖추고 있는 설계자라 하더라도 Figure 1의 새로운 플럭스 배합→시제품 제작→시험검사의 과정을 상당 수 반복할 수밖에 없으며 이 반복횟수의 다소에 따라 소요되는 경비와 시간이 결정된다. ANN을 통해 FCW 설계의 이 반복과정에서 시제품 제작 전에 다양한 플럭스 배합에 대한 용접특성의 유효한 예측치를 얻을 수 있다면 이 반복횟수를 줄일 수 있다.

ANN을 통한 용접특성의 예측의 정확성을 높이기 위해서는 시험검사 등을 통해 얻어지는 데이터 자체의 정확성이 무엇보다 중요하지만 모델의 적절성과 학습방법도 중요하다. 본 연구에서 적용된 FCW 설계데이터는 와이어제조사가 제공하였으며 다년간의 시험검사를 통해 획득된 데이터이므로 일정 수준 이상의 정확성을 확보한 데이터로 간주하고 본 연구에서는 GDR과 Rprop 알고리즘의 2개의 학습방법과 은닉층의 노드수와 학습율의 변화에 따른 예측의 정확도를 조사하여 적절한 모델 설계의 기준을 제시하고자 하였다. 학습율은 0~1 사이의 값을 적용하는 데 일반적으로학습율이 클수록 오차의 수렴속도는 빠르나 수렴오차가 커지는 경향이 나타난다. GDR 모델에서는 통상 0.1~0.5 사이의 값을 적용하지만 데이터 관련성이 복잡한 경우에는 0.01 이하의 값도 적용하기도 한다. Rprop 모델은 수렴속도가 빨라 0.001 이하의 학습율에서도 잘 수렴하고 수렴오차도 매우 적다. 본 연구에서는 GDR의 경우 0.03과 0.001, Rprop의 경우 0.03~0.00001의 학습율을 적용하였다.

Table 2, Table 3은 5개의 모델에 대해서 2개의 학습알고리즘, 2종류의 은닉층 개수와 5가지의 서로 다른 학습율을 적용했을 때의 학습결과를 보여주고 있다. 여기에서 평균오차율은 각 학습데이터에 대해 신경망모델로 예측한 결과와 실제 결과치의 차이의 평균을 의미하며 1~2%내외의 오차율은 학습이 양호하게 이루어졌음을 의미한다. GDR의 경우는 2모델의 2종류의 학습율의 4가지 경우에 대해서 조사해 본 결과 계산횟수가 Rprop에 비해 20배정도 많았음에도 평균오차율이 100%를 상회하여 학습이 잘 되지 않음을 알 수 있었다. 이는 GDR 모델이 FCW 데이터에 대한 용접특성치 예측에 적용하기 어려움을 의미하므로 4가지외의 경우에 대해서는 Rprop 모델에 대해서만 조사하였다. 전반적인 경향은 은닉층의 노드수가 입력층과 비슷한 경우, 그리고 데이터의 유사성이 높고 학습율이 낮을수록 평균오차율이 감소하는 경향을 보여 학습이 잘 이루어짐을 알 수 있었다.

Table 2:

Learning condition and result of model 1 and model 2

Table 3:

Learning condition and result of model 3, model 4 and model 5 using Rprop algorithm and 34 nodes of hidden layer

ANN 모델의 유효성은 그 모델을 적용했을 때의 학습데이터와 검증데이터에 대한 예측치의 오차상태에 의해 정해진다. 학습데이터에 대한 오차가 적은 것은 학습이 잘 이루어졌음을 의미할 뿐 보다 중요한 것은 학습에 사용되지 않은 검증데이터에 대한 오차이다. 이 오차가 적을수록 예측치의 정확도가 높으므로 ANN모델의 유효성은 검증데이터에 대한 오차에 의해 결정된다. 본 논문에서는 예측치의 오차를 1%이하, 1~10%, 10~30%, 30~60%, 60%이상의 5 레벨로 구분하였다. 여기에서 FCW의 용접특성치에 대해 고찰해보면 동일 성분을 갖는 여러 개의 FCW로 동일 조건으로 용접하여 용접특성치를 조사해볼 때 특성치의 차이가 20% 이상으로 나타나는 경우가 적지 않다. 따라서 예측치의 오차가 30%이내는 만족스러운 수준이며 30~60%의 범위도 특성치 변화의 경향 파악에 유용하므로 본 논문에서는 error level 1~3에 속하는 60%이내의 오차를 유효오차로 간주하였다.

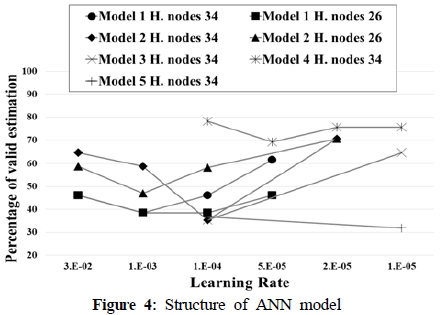
Table 4, Table 5는 여러 학습조건으로 학습한 5개의 모델의 예측치 오차의 분포를 나타낸 것이다. 이 테이블에서 각 오차레벨의 No와 %는 그 오차레벨에 속한 검증데이터세트 수와 전체 검증데이터세트 수에 대한 백분율을 의미한다. 여기에서 유효오차 내에 속하는 검증데이터세트의 비율을 유효예측율로 정하여 ANN 모델의 유효성 평가의 기준으로 하였다. Figure 4는 각 모델의 여러 학습조건에 대한 유효예측율을 그래프로 나타낸 것이다.

Table 4:

Error distribution of estimation result of model 1 and model 2 using Rprop algorithm

Table 5:

Error distribution of estimation result of model 3, model 4 and model 5 using Rprop algorithm

Figure 4:

Structure of ANN model

Figure 4에서 Model 1은 1-4의 학습조건에서 유효예측율이 61.54%, Model 2는 2-4 및 2-8에서 유효예측율이 70.59% 이었으며 Model 3은 3-2에서 64.71의 예측율을 보였다. Model 1~3은 데이터의 유사성이 높아 학습데이터에 대한 예측오차는 매우 적지만 학습데이터가 적어 학습을 통한 일반화된 상관관계 수립에는 미치지 못한 것으로 판단된다. Model 4는 학습율이 다른 4조건에서도 70%를 상회하는 양호한 유효예측율을 보였다. 특히 유효예측율의 내용에서도 정확도가 높은 error level 2이하가 30~40%를 차지하여 예측기능이 우수한 것으로 나타났다. 이는 Model 1~3에 비해 학습데이터가 많으면서도 탄소강용이라는 일정수준의 데이터 유사성을 가지고 있어 비록 학습데이터에 대한 오차가 다소 높아졌지만 학습에 의해서 입력항목과 출력항목 사이의 상관관계가 잘 수립된 점에 기인한 것으로 판단된다. 반면 Model 5는 학습율이 매우 낮은 0.00001에서도 유효예측율이 40%에 미치지 못하였다. 이는 Model 5는 이질적인 탄소강과 스테인리스강용 데이터를 모두 대상으로 하여 데이터의 유사성이 낮아 반복횟수 8,000,000회에 이르는 가장 긴 학습시간을 투입했음에도 평균오차율이 25% 에 이를 정도로 학습이 충분히 되지 않았음에 원인이 있다고 볼 수 있다.

5. 결 론

본 연구에서는 학습효율이 뛰어난 탄력적 오류역전파 ANN을 적용한 FCW 설계데이터의 용접특성치 예측에 관한 연구를 수행하였다. 이를 위해 적용대상이 다른 5종류의 FCW 데이터에 대한 5개의 ANN 모델을 만들고 다양한 학습조건으로 학습을 시켜 적절한 학습조건을 조사하고 검증데이터를 이용하여 학습된 ANN 모델의 유효성을 검증하였다. 이를 통해 다음과 같은 결론을 얻을 수 있었다.

• (1) FCW 설계를 위한 ANN 모델은 대상 데이터의 유사성이 있고 데이터의 양이 충분할수록 모델의 유효성이 높다. 본 연구에서는 데이터의 유사성이 있고 데이터 양도 충분한 Model 4의 경우 유효예측율이 높았으며 데이터의 유사성은 높으나 양이 적은 Model 1~3은 제한적인 범위에서 유효성이 있음을 알 수 있었다. 데이터양은 많았지만 데이터의 유사성이 낮은 Model 5의 경우는 유효예측율이 매우 낮았다.
• (2) 널리 활용되고 있는 일반화된 델타 규칙 학습알고리즘은 오차 수렴시간이 길고 수렴 오차값이 커 FCW 용접특성치 예측에 적절하지 않은 것으로 판명되었으며 탄력적 오류역전파 알고리즘은 이러한 문제점 없이 적용이 가능함을 알 수 있었다.
• (3) 은닉층의 노드수는 입력층과 출력층 노드 수 사이의 값이 사용되지만 본 연구에서 비교해본 결과 입력층 노드수와 동일하게 하였을 때 양호한 결과를 보여주었다.
• (4) FCW 용접특성치 예측의 경우 데이터 유사성이 높아도 학습율은 0.0001 이하의 낮은 학습율을 적용하는 것이 바람직하다. 본 연구에서는 Model 1~3에서 0.00005이하의 학습율일 때 유효예측율이 60%이상, Model 4에서는 0.0001이하의 학습율일 때 유효예측율이 70% 이상을 나타내었다.

References

• H. D. Im, C. H. Choi, J. H. Jung, and W. Kil, “The latest technology development tends of flux cored wire”, Journal of Welding and Joining, 34(6), p1-10, (2016), (in Korean). [https://doi.org/10.5781/jwj.2016.34.6.1]
• I. W. Han, and S. T. Hong, “Development trend of steel and welding consumables for pressure vessel”, Journal of Welding and Joining, 28(2), p5-12, (2010), (in Korean). [https://doi.org/10.5781/kwjs.2010.28.2.005]
• S. C. Park, S. S. Kang, J. H. Yoon, and G. Y. Kim, “The prediction of fatigue life of muffler by artificial neural network”, Journal of the Korean Society of Marine Engineering, 37(8), p869-876, (2013), (in Korean). [https://doi.org/10.5916/jkosme.2013.37.8.869]
• J. H. Lee, J. C. Kim, and D. H. Seo, “A study on image caption algorithm based on object detection”, Journal of the Korean Society of Marine Engineering, 41(7), p683-689, (2017), (in Korean). [https://doi.org/10.5916/jkosme.2017.41.7.683]
• J. Y. Park, “Optimal welding condition for the inclined and skewed fillet joints in the curved block of a ship (I)”, Journal of Ocean Engineering and Technology, 18(6), p79-83, (2004), (in Korean).
• M. S. Kim, S. M. Shin, D. H. Kim, and S. H. Rhee, “A study on the algorithm for determining back bead generation in GMA welding using deep learning”, Journal of Welding and Joining, 36(2), p74-81, (2016), (in Korean). [https://doi.org/10.5781/jwj.2018.36.2.11]
• J. H. Cho, “Prediction of arc welding quality through artificial neural network”, Journal of Welding and Joining, 31(3), p44-48, (2013), (in Korean). [https://doi.org/10.5781/kwjs.2013.31.3.44]
• M. Riedmiller, and H. Braun, “A direct adaptive method for faster backpropagation learning: The RPROP algorithm”, Proceedings of the IEEE International Conference on Neural Networks, San Francisco, p586-591, (1993). [https://doi.org/10.1109/icnn.1993.298623]
• Z. Xiong, Y. Zhang, L. Ou, and L. Li, “Two-phases parallel neural network algorithm based on RPROP”, 2005 IEEE Region 10 Conference, p1-6, (2005). [https://doi.org/10.1109/tencon.2005.301307]
• C. Igel, and M. Huesken, “Improving the Rprop learning algorithm”, Proceedings of the Second International Symposium on Neural Computation, NC’2000, p115-121, (2000).
• D. M. Hawkins, “The problem of overfitting”, Journal of Chemical Information and Computer Sciences, 44(1), p1-12, (2004). [https://doi.org/10.1021/ci0342472]