소형선박용 고분자 전해질 연료전지 스택 모델 개발

1. 서 론

선박으로부터의 환경오염 문제를 방지하기 위한 다양한 규제가 시행되고 있다[1]. 이를 해결하기 위하여 방안으로 엔진 배기가스에 포함된 대기오염물질의 배출을 저감하기 위한 방법으로 추가적인 대기오염방지 장치의 설치, 대기 오염이 적은 연료의 사용, 기관 시스템의 전반적인 효율을 개선하는 방법 등이 사용되어지고 있다. 하지만 이러한 방법으로는 대기 환경오염 문제를 근본적으로 해결할 수 없기 때문에 새로운 친환경 추진시스템 기술 도입이 필요하다. 이에 따라 새로운 기술 중 하나로 연료전지를 선박에 탑재하는 연구가 활발히 진행되어지고 있다[2].

연료전지는 일종의 발전장치로써 수소의 연소를 통해 발생되는 열을 사용하는 것이 아니라 수소의 화학에너지를 직접 전기에너지로 변환 시키는 장치이며 이 때 배출되는 물질은 대부분 물이기 때문에 대기오염의 문제가 없고 친환경적이며 기존의 내연기관 등의 시스템 보다 효율이 높은 특징을 가지고 있다. 특히 PEMFC은 상온에서 작동하며 부피와 무게대비 전류밀도가 높고 시동속도가 빠르다는 점에서 소형선박의 주전원으로 주목받고 있다[3].

국내에서는 20m 길이의 소형 연료전지선박이 개발되어 실증실험이 완료되었다[4]. 이 선박은 50 kW급 PEMFC (25kW급 모듈 2기)를 탑재하였으며, 47kWh 리튬이온 배터리를 사용하여 추진시스템을 구동하기 위한 주전원과 보조기기들을 위한 보조전원을 모두 공급할 수 있도록 시스템이 구성되어져 있다. 이 실증실험을 통해 소형선박에서 오염배출이 큰 내연기관을 오염물질이 전혀 없는 PEMFC로 대체할 수 있음을 확인하였다. 하지만, 실증실험의 기간이 길지 않아 선박 운항 중의 연료전지 배터리 하이브리스 시스템에 대한 다양한 특성들에 대한 파악은 미흡하였다고 판단되며 이에 대한 더 많은 연구가 필요할 것이다. 하지만 실증운항을 위한 예산과 시간이 한정되어 있으므로 모든 연구를 실험적으로 진행하기에는 많은 어려움이 현실적으로 존재한다. 따라서 본 연구에서는 소형선박에 탑재된 25kW급 연료전지 스택 모듈의 운전특성을 파악하기 위한 PEMFC 스택 모델을 개발하였으며, 실증운항 데이터와 비교 검토하고 연료전지 스택의 운전온도에 따른 스택의 성능특성에 관하여 검토하였다.

2. 해석모델

2.1 시스템 및 모델구성

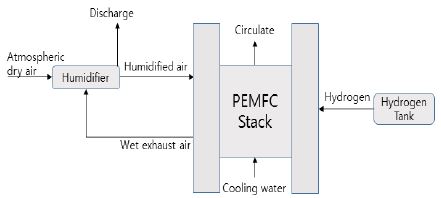
Figure 1은 PEMFC 시스템 구성도를 나타내고 있다. 그림 중앙에 보이는 연료전지 스택으로는 가습기를 통해 가습된 대기 중의 공기가 공급되며 연료전지 스택에서 반응 후 생성된 물과 공기는 가습기로 다시 공급되어 공급 공기의 가습원으로서 사용되고 대기로 배출된다. 우측으로 압축 수소탱크를 통해 수소가 공급되며 사용되지 않고 남은 수소는 재순환 되어 연료전지 스택으로 다시 공급된다. 대기의 건조한 공기는 가습기로 공급된 후 약 95~98%로 가습되어 연료전지 스택으로 공급되는데 이 때, 수분의 공급 및 가열원은 연료전지 스택에서 배출된 고온다습의 공기이기 때문에 수분과 열을 추가적으로 공급할 필요가 없어 효율이 높고 장치가 간단해진다. PEMFC 작동 중 스택에서 발생되는 열은 냉각수에 의하여 냉각되어 적정한 스택의 운전온도를 유지한다. 스택에서 배출되는 고온의 냉각수는 선박의 여러 가지 열원으로 사용 및 냉각 된 후 스택의 냉각수로 다시 공급된다.

Figure 1:

Configuration of PEMFC system

본 연구에 사용된 데이터는 협력사에 의해 제공된 실험값을 바탕으로 실험 결과와 동일한 연료전지 스택의 운전조건에서 동일한 결과를 얻을 수 있는 스택모델의 개발이 목적이다. 연료전지 스택 운전온도는 50℃, 60℃, 68℃의 경우 실험값을 충족할 수 있는 모델을 개발하였다. PEMFC 시스템 모델은 Mathwork사의 Matlab & Simulink를 사용하여 개발하였다.

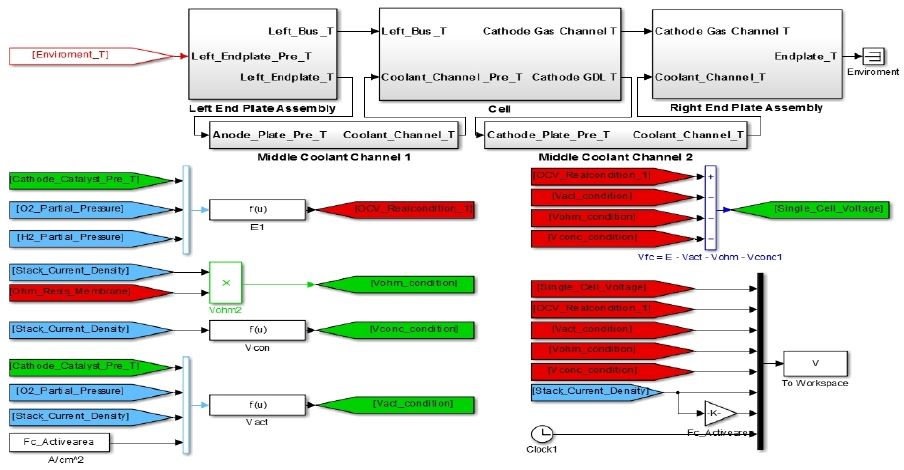
Figure 2는 시뮬레이션 모델링의 전체 구성도를 나타내고 있다. PEMFC 스택 및 BOP로 구성되며, 스택은 Membrane-Electrode-Assembly (MEA), 촉매층, 가스확산층, 가스유로로 구성되어있고, BOP는 가습기, 열교환기, 냉각수 펌프, 에어 블로워, 수소 탱크로 구성되어있다.

Figure 2:

Configuration of modeling

Figure 2의 상부를 살펴보면 스택 내부에서의 열전달에 대한 모델을 나타내고 있다. 하부에는 전압 및 전류를 계산하기 위해 각종 손실전압에 대한 계산 모델이다. 우측 하단의 모델 블록을 통해서 계산된 결과 값들이 출력되어 저장된다.

2.2 물성치 및 지배방정식

Table 1은 본 연구에서 사용되어진 연료전지 스택의 사양을 나타내고 있다. Table 2는 본 연구에서 도출한 연료전지 스택 모델에 사용되어진 지배방정식에 대한 각종 계수 값들이다. 연료전지 스택의 I-V 특성 방정식은 다음의 식 (1)과 같이 나타낼 수 있다.

$\[ V_i=E_i-{\eta }_{i,act}-{\eta }_{i,ohm}-{\eta }_{i,con} \]$

(1)

Table 1:

Specifications of the stack

Table 2:

Consistence value

식 (1)의 E_i는 개회로 전압을 나타내며, η_i,act는 활성화손실, η_i,ohm는 저항손실, η_i,con농도손실을 나타낸다. 스택의 전압은 여러 가지 비가역적인 요소에 의해 위 식과 같은 각종 손실들이 일어나므로 개회로전압보다 낮은 값을 갖는다.

개회로 전압은 다음의 식 (2)로 나타낼 수 있다[5].

$\[ E_i=1.229-0.85\times {10}^{-3}\left(T_i-298.15\right)+4.3085\times {10}^{-5}{T}_i\left[\text{ln}\left(p_i,H_2\right)+\frac{1}{2}\text{ln}\left(p_i,O_2\right)\right] \]$

(2)

활성화 전압손실은 식 (3)과 같이 나타낸다[5]-[7].

$\[ {\eta }_{i,act}={\xi }_1+{\xi }_2{T}_i+{\xi }_3{T}_i\ln \left(C_i,O_2\right)+{\xi }_4{T}_i\ln \left(T\right) \]$

(3)

식 (3)의 ξ의 값들은 Table 2의 값을 사용하였다.

저항전압손실은 식 (4)와 같이 나타낸다[8][9].

$\[ {\eta }_{i,ohm}=i{R}_{i,ohm}=\frac{i{t}_{mem}}{{\sigma }_{i,men}} \]$

(4)

식 (4)에서 t_mem 는 막의 두께를 나타내며, σ_i,mem은 이온전도율이다.

이온전도율은 다음의 식 (5)와 같이 나타낼 수 있다[8][9].

$\[ {\sigma }_{i,mem}=\sigma \text{exp}\left[C_1\left(\frac{1}{303}-\frac{1}{T_i}\right)\right] \]$

(5)

식 (5)에서 σ 는 다음의 식 (6)으로 나타낼 수 있다[6][7].

$\[ \sigma =C_2{\lambda }_{i,mem}-C_3 \]$

(6)

위 식 (6)에서 λ_i,mem는 막의 함수율을 나타내며, 다음의 식 (7)과 같이 나타낼 수 있다[9][10].

$\[ {\lambda }_{mem}=\frac{C_{H_{2}O,mass}/M_{H_{2}O}}{\frac{{\rho }_{dry,mem}}{M_{mem}}-0.0126\frac{C_{H_{2}o,mass}}{M_{H_{2}O}}} \]$

(7)

수분의 이동에 관한 질량변화율은 다음의 식 (8)과 같이 나타낼 수 있다[9][10].

$\[ \begin{array}{c}{\dot{m}}_{water,mem}=\frac{d\left(C_{H_{2}O,mass}{A}_{cell}{t}_{mem}\right)}{dt}\hfill \\ =W_{ele,mem,anode}-W_{ele,mem,cathode}+W_{diff,mem,anode}+W_{diff,mem,cathode}\hfill \end{array} \]$

(8)

농도 전압손실은 다음의 식 (9)와 같이 나타낼 수 있다[6][7].

$\[ {\eta }_{i,con}=-b\text{ln}\left(1-\frac{i}{i_{\text{max}}}\right) \]$

(9)

스택의 전압은 모든 단셀 전압의 합으로써 다음의 식 (10)으로 나타낼 수 있다.

$\[ V_{stack}=\sum _i{V}_{i,cell} \]$

(10)

에너지보존식은 다음의 식 (11)로써 나타낼 수 있다[11].

$\[ \sum _i{C}_{p_i}{C}_{i,mass}{A}_{cell}{t}_{CV}\frac{d{T}_{CV}}{dt}=\underset{mass flow inlet}{\underbrace{\sum W_{inlet}{A}_{cell}{C}_{p_i}\left(T_{inlet}-T_{CV}\right)}+{\dot{Q}}_{convection}+}{\dot{Q}}_{conduction}+{\dot{Q}}_{sources} \]$

(11)

스택에서의 물질전달에 대한 질량변화율은 다음의 식 (12)와 같이 나타낼 수 있다[9][11].

$\[ \frac{d{m}_{v,tr}}{dt}=D_{w,eff}\frac{C_{shell}-C_{tube}}{t_m}{M}_v{A}_{mem} \]$

(12)

3. 해석결과

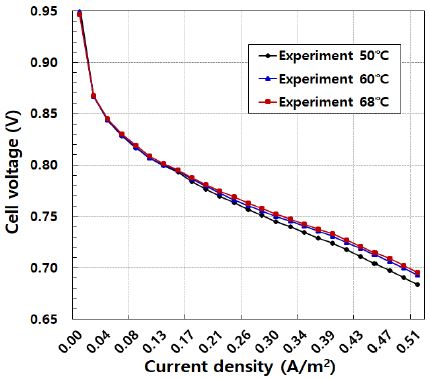
Figure 3은 연료전지 스택의 운전온도가 50℃, 60℃, 68℃ 인 경우에 대한 따른 전압-전류 특성에 대한 실험 결과를 나타낸 것이다. 전류밀도가 0∼0.17(A/m²)인 영역에서는 스택의 운전 온도변화에 따른 전압의 변화는 거의 없음을 알 수 있다. 저 전류밀도 영역에서의 전압손실은 활성화과전압이 가장 큰 영향을 미친다. 활성화과전압을 저감하는 방법으로는 스택 운전온도의 증가, 효과적인 촉매의 사용, 전극표면의 거칠기 증가, 반응물질의 농도 증가 및 공급가스의 압력 증가 등이 있다. 본 연구에서실험은 연료전지 스택의 운전온도만을 변경하였기 때문에 활성화과전압은 운전온도의 영향을 받게 된다. 운전온도의 증가는 활성화과전압을 감소시킬 수 있지만 본 연구의 연료전지 스택 운전온도 범위에서는 큰 영향을 미치지 않음을 알 수 있다.

Figure 3:

I-V characteristics of the cell

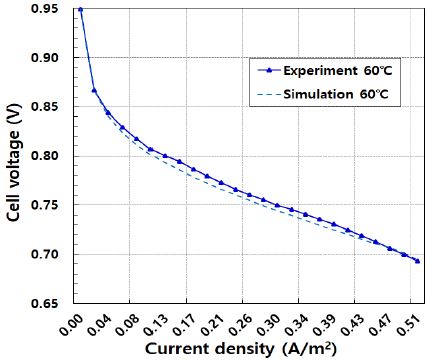
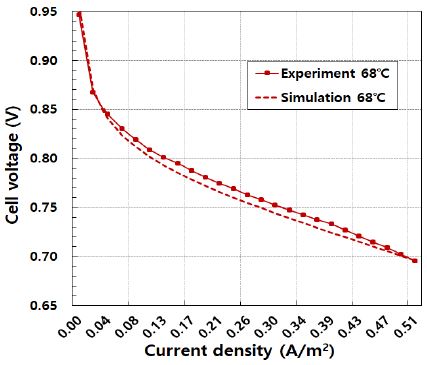
전류밀도가 0.17(A/m²)이상의 영역에서는 스택의 전류밀도가 증가함에 따라 연료전지 스택 운전온도가 낮은 경우 전압이 더욱더 낮아짐을 알 수 있다.

전압강하는 전해질 막을 통과하는 이온의 흐름 및 전자의 흐름에 대한 저항으로 발생하게 되며 일반적으로 전류밀도에 대하여 선형적으로 비례하는 값을 가진다. 또한, 스택의 운전온도가 증가하면 공기의 포화수증기압이 증가하여 연료전지 내부를 흐르는 공기가 더 많은 양의 수분을 흡수할 수 있게 된다. 이에 따라 막의 수분 함량이 낮아지게 되어 저항 전압손실이 증가하여 스택의 전압이 감소하는 특징을 보이게 된다. 본 연구에서는 연료전지 스택의 운전 온도가 높을수록 저항 전압손실이 작아 셀의 전압이 높음을 알 수 있다. 이는 막의 가습정도가 적정하게 유지되면 연료전지 스택의 운전온도가 높은 경우가 막으로의 기체 확산성 및 이온 전도도가 증가하여 저항 과전압이 감소하기 때문이다.

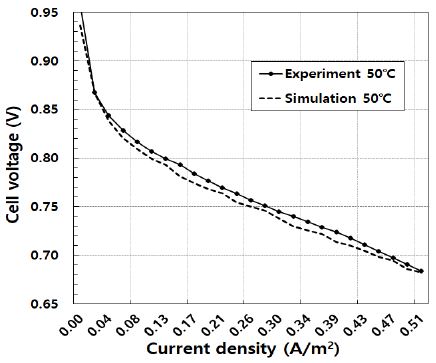
Figure 4 ~ Figure 6은 연료전지 스택의 운전온도가 50℃, 60℃, 68℃ 인 경우에 대한 따른 전압-전류 특성에 대한 실험값과 본 연구에서 개발한 모델을 활용한 계산 결과를 비교하여 나타낸 것이다. 계산 값은 실험값과 비교하였을 때 각각의 조건에서 약 1%s이내의 오차를 보임을 알 수 있다. 실험값과 계산값에 대한 오차가 발생하는 이유는 본 연구에서 고려되어진 손실전압 이외의 각종 기생손실전압을 수학적으로 고려하지 않았기 때문으로 판단된다.

Figure 4:

Comparison of the cell voltage between the experiments and the simulation

Figure 5:

Comparison of the cell voltage between the experiments and the simulation

Figure 6:

Comparison of the cell voltage between the experiments and the simulation

4. 결 론

본 연구에서는 50kW급 고분자 전해질 연료전지의 스택 모델을 개발하여 연료전지 스택의 운전온도에 따른 성능특성에 관하여 검토하여 본 연구의 범위에서 다음과 같은 결론을 얻었다.

• (1) 저전류 밀도 영역에서의 연료전지 스택의 운전온도는 셀 전압에 큰 영향을 미치지 않는다.
• (2) 전류밀도가 0.17(A/m²)이상의 영역에서는 연료전지 스택의 운전온도가 높을 경우 저항 전압손실이 감소하여 셀의 전압이 높다.
• (3) 계산 값과 실험값을 비교한 결과 각각의 조건에서 약 1%의 오차 범위 이내로 실험결과를 모사할 수 있었다.

References

• International Maritime Organization (IMO), Report of the Marine Environment Protection Committee on its 65th Session, (2013).
• M. H. Kim, “Analysis on the technology R&D of the fuel cell systems for power generation in ships”, Journal of the Korean Society of Marine Engineering, 31(8), p924-931, (2007), (in Korean). [https://doi.org/10.5916/jkosme.2007.31.8.924]
• J. Larminie, and A. Dicks, Fuel Cell Systems Explained, John Wiley & Sons Ltd, (2003).
• C. H. Choi, S. Yu, I. S. Han, B. K. Kho, D. G. Kang, H. Y. Lee, M. S Seo, J. W. Kong, G. Kim, J. W. Ahn, S. K. Park, D. W. Jang, J. H. Lee, and M. Kim, “Development and demonstration of PEM fuel-cell-battery hybrid system for propulsion of tourist boat”, International Journal of Hydrogen Energy, 41(5), p3591-3599, (2016). [https://doi.org/10.1016/j.ijhydene.2015.12.186]
• J. C. Amphlett, R. M. Baumert, R. F. Mann, B. A. Peppley, P. R. Roberge, and T. J. Harris, “Performance modeling of the ballard mark IV solid polymer electrolyte fuel cell”, Journal of The Electrochemical Society, 142(1), p1-8, (1995). [https://doi.org/10.1149/1.2043866]
• Z. J. Mo, X. J. Zhn, L. Y. Wei, and G. Y. Cao, “Parameter optimization for a PEMFC model with a hybrid genetic algorithm”, International Journal of Energy Research, 30(8), p585-597, (2006). [https://doi.org/10.1002/er.1170]
• J. M. Correa, F. A. Farret, L. N. Canha, and M. G. Simoes, “An electrochemical-based fuel-cell model suitable for electrical engineering automation approach”, IEEE Transactions on Industrial Electronics, 51(5), p1103-1112, (2004). [https://doi.org/10.1109/tie.2004.834972]
• T. V. Nguyen, and R. E. White, “A water and heat management model for proton‐exchange‐membrane fuel cells”, Journal of The Electrochemical Society, 140(8), p2178-2186, (1993). [https://doi.org/10.1149/1.2220792]
• T. E. Springer, T. A. Zawodzinski, and S. Gottesfeld, “Polymer electrolyte fuel cell model”, Journal of the Electrochemical Society, 138(8), p2334-2342, (1991).
• S. K. Park, and S. Y. Choe, “Dynamic modeling and analysis of a 20-cell PEM fuel cell stack considering temperature and two-phase effects”, Journal of Power Sources, 179(2), p660-672, (2008). [https://doi.org/10.1016/j.jpowsour.2008.01.029]
• Y. Shan, and S. Y. Choe, “Modeling and simulation of a PEM fuel cell stack considering temperature effects”, Journal of Power Sources, 158(1), p274-286, (2006). [https://doi.org/10.1016/j.jpowsour.2005.09.053]