Study on the searching period of MPPST algorithm in partial-shading conditions
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Solar panels installed on a single-point mooring (SPM) system will be installed in many directions in application such as rotation by waves. In these solar panel configurations, partial-shading effects occur. When using the maximum power point tracking algorithm, power generation loss is caused by the partial-shading effect. Therefore, the maximum power point searching and tracking (MPPST) algorithm, which includes the searching motion on a regular basis, is advantageous for increasing power generation efficiency. When using the MPPST algorithm, the more frequent the searching operations, the more advantageous it is to find the maximum power point. However, there is also a problem in that the period of searching is lost. In this research, we study the optimal searching period of the MPPST algorithm applied to SPM.
Keywords:
Maximum power point tracking (MPPT) algorithm, Maximum power point searching and tracking (MPPST) algorithm, Solar generation system, SPM system1. Introduction
A single-point mooring (SPM) system is a single-mooring-type offshore plant that plays a role in the mooring of ships and transport of oil and gas by connecting onshore facilities or oil tankers. Because the SPM system is installed offshore, it uses a stand-alone power system. Recently, the power demand of SPM systems has increased according to such added functions as an auto identification system (AIS), as well as trends such as the enlargement of ships. To complement this, renewable energy, such as solar power generation, is used as a power source. However, a solar generation system installed in a point-mooring-type offshore plant, such as SPM, is different from a land-based system, and a design considering the rotation of the structure and influence of waves is necessary. Various algorithms have been investigated to improve the power generation efficiency of solar photovoltaic systems applied at sea. There are the perturb and observe (P&O) maximum power point tracking (MPPT) algorithm, the incremental conductance (IncCnd) MPPT algorithm, etc. for the controller of a solar generation system [1]. In addition, the maximum power point searching and tracking (MPPST) algorithm reduces loss caused by the partial-shading effect [2]. In this research, a study was conducted to improve MPPST power generation efficiency.
2. Solar generation system
2.1 Characteristics of Solar Generation System
A solar power generation system converts solar energy into electric energy by utilizing photovoltaic effects. These solar cells are connected in series and called modules, and they usually refer to a single solar panel. In addition, the solar array is constructed by connecting the panels in series or in parallel. Depending on the configuration of the array, the characteristics of solar panels, such as voltage and current, change.
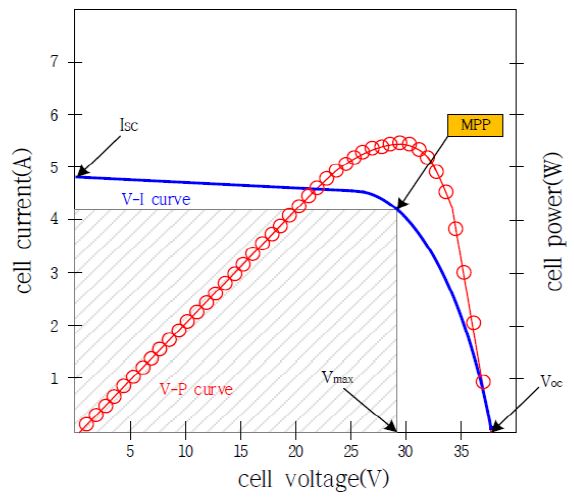
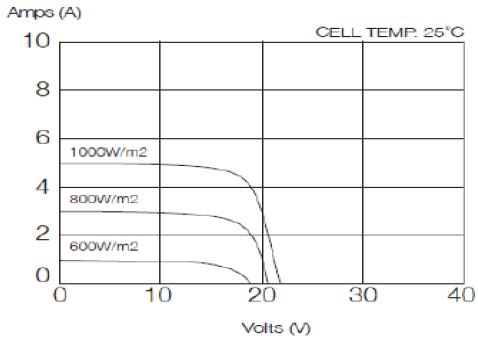
Figure 1 is a solar cell characteristic curve showing the current and output power varying according to the voltage applied to the solar cell. In Figure 1, ISC is the short-circuit current, and VOC is the open-circuit voltage. Vmax refers to the voltage at the maximum power point (MPP) at which the power generated from the irradiation is maximized. Therefore, when designing a solar power generation system, it is necessary to configure solar panels as a serial–parallel array according to the characteristics of the system using power. Solar power generation systems used in offshore structures, such as buoys and the SPM system, are generally operated independently of the power storage system. Using a buck converter between the solar array and load system or battery makes power conversion more stable. Furthermore, by changing the switching duty ratio of the converter, the power generated by the solar array can be controlled to the maximum output.
2.2 MPPT (Maximum Power Point and Tracking) Algorithm
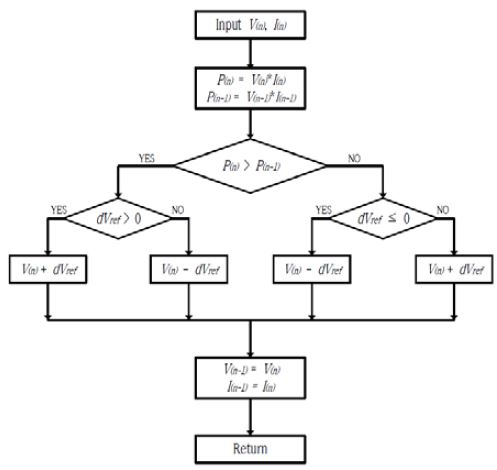
The solar power generation system is generally influenced by the temperature of the solar module and the quantity of irradiation into solar module, but if the state of the light quantity and the temperature are same, the output power changes depending on the state of the system voltage. It is the same for the output voltage of the buck converter. If it is possible to follow continuously the voltage state that produces the maximum power, the solar power generation system can produce electric power under the maximum power generation condition. As described above, the P&O algorithm, IncCnd algorithm, etc. provide a method of checking the voltage state and following the MPP. Figure 2 shows the P&O algorithm that is used commonly.
The P&O algorithm follows the MPP by comparing the output value at the previous voltage and the output value at the change voltage while changing the voltage value. The P&O algorithm has the advantage that the algorithm is simple, and the calculation is fast.
3. Partial shading effect
Two solar panels are installed in reverse to obtain stable output power irrespective of the rotation of the SPM system. The solar panels can generate power at the MPP through the solar power generation system, which contains a buck converter. In addition, the generated power can be stored in batteries or used in loads, such as a hydraulic power unit motor, foghorn, lights, etc., via the central control panel.
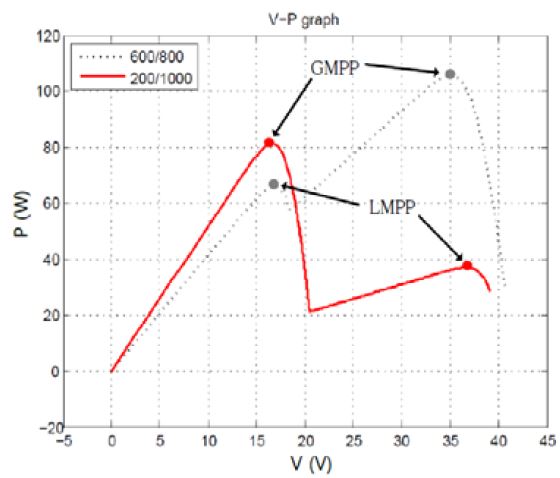
The partial-shading effect is a phenomenon in which the characteristic curve changes when the amount of the irradiation into the solar cell becomes different. In the solar power generation system installed in the SPM system, if solar panels are installed in various directions to obtain a stable output power, the amount of irradiation onto each solar panel differs, and it becomes vulnerable to the partial-shading effect. Figure 3 shows the characteristic curve of the solar power generation system under the partial-shading effect.
The characteristic curve of the partial-shading effect has several MPPs that can be judged as the MPP by the MPPT algorithm. The MPP generated in each zone is the local maximum power point (LMPP), and the MPP that outputs the highest generated power among them is the global maximum power point (GMPP). The MPPT algorithm compares the previous output value with the current output value of a solar power generation system, and it changes the voltage to a higher output. Therefore, when the voltage exists in the section where the LMPP exists, the power generation loss that occurs is as much as the difference between the GMPP and LMPP, because it cannot follow the GMPP. The partial-shading effect occurs when solar panels are installed in several directions for the stable supply of power, such as the proposed solar power generation system. The effect occurs when there is a difference of irradiation between panels, and the shape of the V–P curve is also affected. When the amount of irradiation incident on both panels differs, the open-circuit voltage (VOC) and the short circuit current (ISC) are different, and the voltage at MPP (VMPP), current at MPP (IMPP), and output power at MPP (PMPP) also become different. The following expressions show the currents and voltages generated by the two panels connected in series [3][4].
| (1) |
| (2) |
| (3) |
Two characteristic curves are superimposed on the photo current according to the amount of irradiation incident on the panels. The shape of the characteristic curve in which the partial-shading effect occurs can be divided into different types. First is the case of the GMPP on the right side. Second is the case of the GMPP on the left side. In addition, there is the case in which there are the same two GMPPs. Because the shape of these characteristic curves is influenced by the photocurrent, it is determined based on the difference in irradiation of each panel.
4.MPPST(Maximum Power Point Searching and Tracking) algorithm
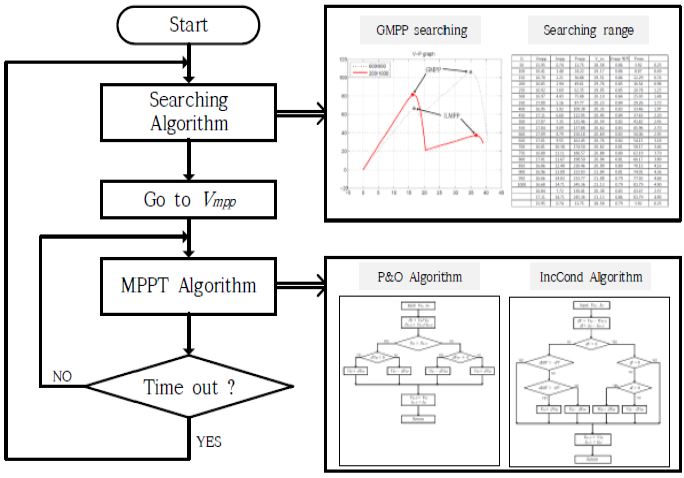
The MPPST algorithm is an algorithm adding searching operation on the MPPT algorithm. For a solar power generation system installed in a mooring-type offshore plant, sudden rotation and different irradiation on the panels can occur. Thus, the system is vulnerable to the partial-shading effect. In a solar power generation system where the partial-shading effect occurs, the MPPT algorithm could cause power generation loss because of the LMPP. However, the MPPST algorithm finds the GMPP by searching the entire voltage section from the open-circuit voltage to 0. Figure 4 shows the MPPST algorithm.
The MPPST algorithm consists of two parts. A searching algorithm section finds the MPP by changing the PWM(pulse width modulation) duty ratio from the open-circuit voltage to 0, and a tracking algorithm compares the output value of the previous cycle and the current cycle to follow the MPP. This algorithm is efficient for avoiding the LMPP and finding the GMPP, and it is possible to reduce the problem of the MPPT algorithm not following the MPP correctly when the V–P curve changes frequently because of the change of irradiation on each panel.
The searching does not operate near the MPP. It changes the voltage from 0 to VOC and results in searching loss. Because the irradiation varies with time, the position of the GMPP of the solar generation system also moves. For that reason, it is necessary to search and correct the GMPP position by searching again when the operation time of the MPPT algorithm ends. In conclusion, the searching operation changes the voltage applied to the solar panel and finds the voltage with the highest power generation; therefore, frequent searching operation decreases the power generation efficiency. However, too long a searching operation cycle cannot follow the GMPP properly.
In the conventional MPPST controller, the searching operation is performed at intervals of 5 to 10 min.
5.Simulation
5.1 Solar Panel
The target solar panel was selected for the modelling of the solar panel. ATEX SM085Ex was simulated, and the specifications are shown in Figure 5 and Table 1.
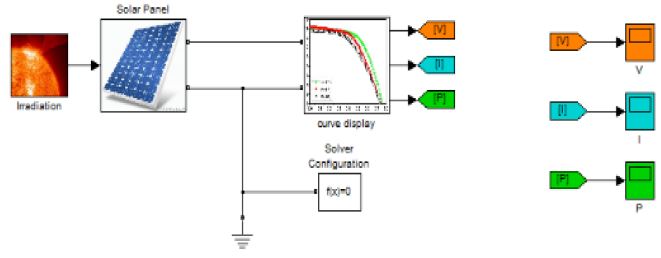
The simulation was constructed as follows based on specifications of solar panels by using the Matlab Simulink program. The simulation model consisted of an input of irradiation, solar panel, curve display that makes the characteristic curve with changing voltage, and a solver configuration that sets the analysis method for the physical model. In Figure 6, this model consists of a solar irradiation model, a solar panel model, and a curve display model.
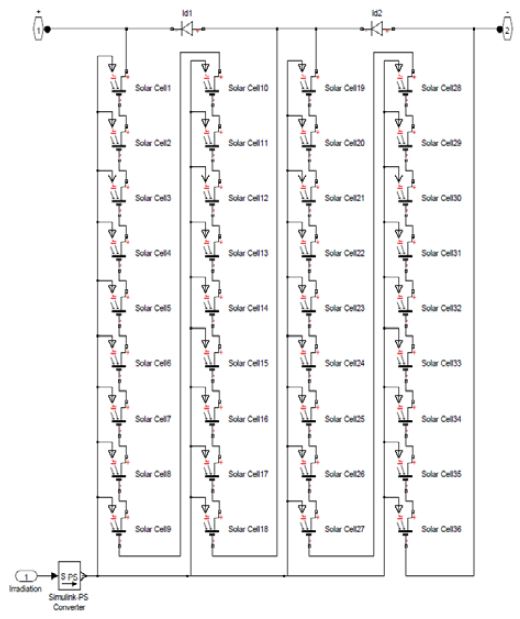
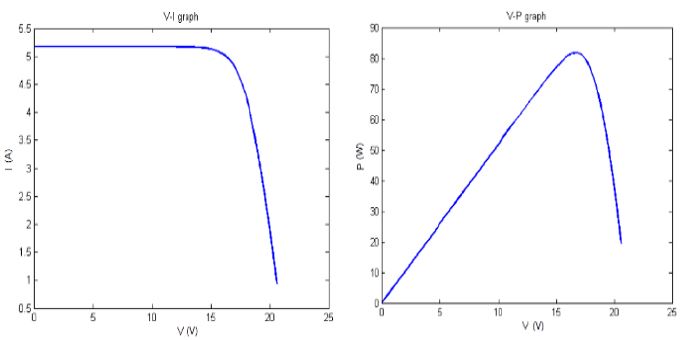
The inside of the solar panel section is composed of 36 solar cells. Figure 7 shows that the solar panel model consists of a solar cell model. The characteristic value of the target solar panel is entered for each solar cell. A characteristic curve of the solar panel model was derived as shown in Figure 8.
In the V–I curve in Figure 8, the short-circuit current is 5.14 A, the open-circuit voltage is 22.03 V, and the maximum power with the V–P curve is at 85 W. The characteristic curves are similar to the ATEX-SM085Ex data sheet. The results are consistent with the ATEX-SM085 specification and are suitable for use as a simulation model.
5.2 Characteristic Curve of the Solar Panel Array
Next, to confirm the characteristic curve when the partial-shading effect occurred, two solar panels were connected in series, and the generation power output according to the difference of irradiation on each panel was simulated Table 2 shows the simulation conditions.
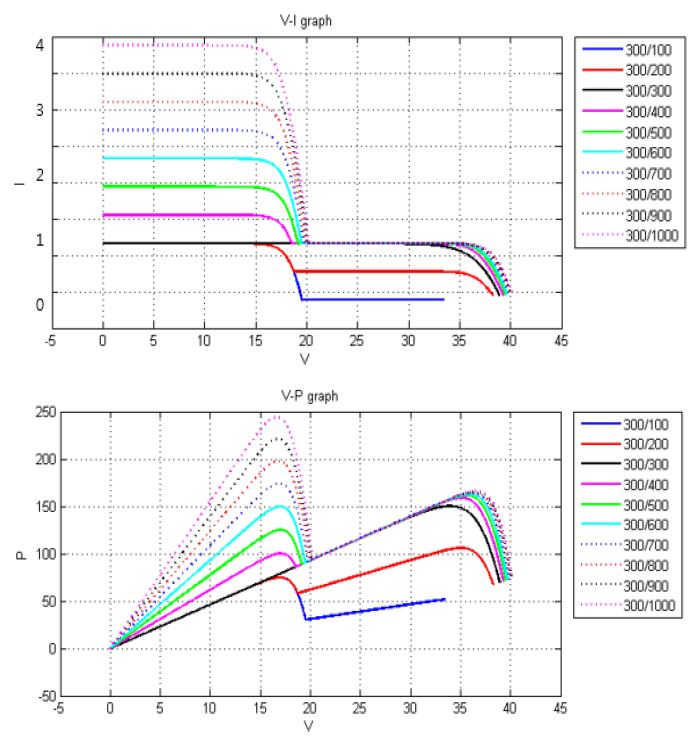
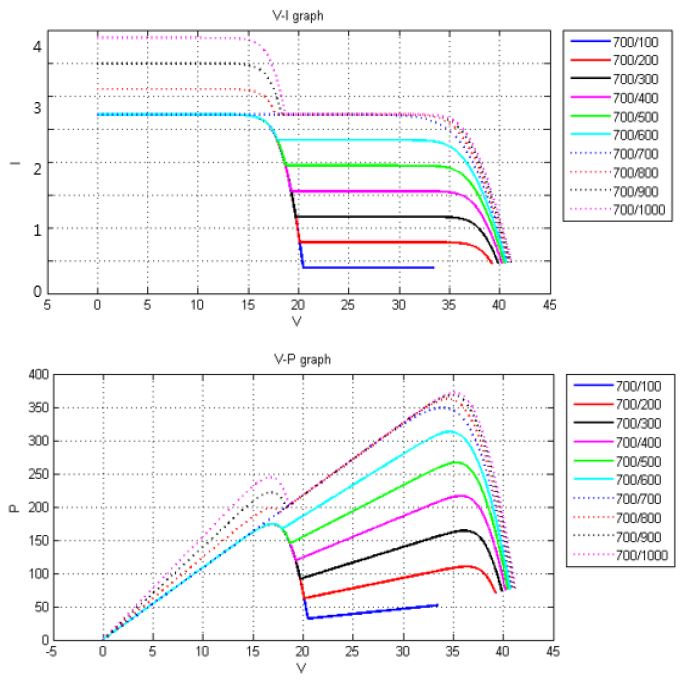
The results of the simulation in Figure 9, Figure 10, and Figure 11 were obtained when irradiation on Panel 1 was 300, 500, and 700.
The below results show that the GMPP occurs on the left side of the graph when the difference of irradiation between the panels is large; the GMPP occurs on the right side of the graph when the light amount difference is small [5].
5.3 Daily Irradiation Simulation
Changes in the amount of irradiation on the solar panels were simulated under the following conditions. Table 3 shows the condition of daily irradiation.
Latitude, longitude, and date information were input to the daily irradiation simulation to calculate the local time, time angle, altitude angle, zenith angle, and azimuth angle. Simulation results show that the solar irradiance and generated power is affected by the installation angle [4].
5.4 MPPT Algorithm
Simulations were conducted in two directions for the solar generation system with two panels. Figure 12 shows the change in the generated voltage according to the time, and Figure 13 shows the output according to the time.
In Figure 12, the voltage of the GMPP changes continuously as a partial-shading effect occurs in the amount of irradiation on the solar panels according to time. When the MPPT algorithm operates, the power generation state stays at the MPP. However, it is not known whether MPP is GMPP or LMPP. In addition, the change of the GMPP is large near sunrise and sunset when the difference in the amount of irradiation on the two panels is great.
In Figure 13, the power generation in the GMPP is always changed by the partial-shading effect. When the MPPT algorithm cannot follow GMPP and it generates the power in the LMPP, the difference in power generation greatly differs. The simulation shows that the generated voltage and output hardly change in the MPPT algorithm. This is because the MPPT algorithm searches the nearest MPP at which the algorithm is started. The MPPT algorithm cannot determine whether this MPP is the GMPP or LMPP.
5.5 MPPST Algorithm
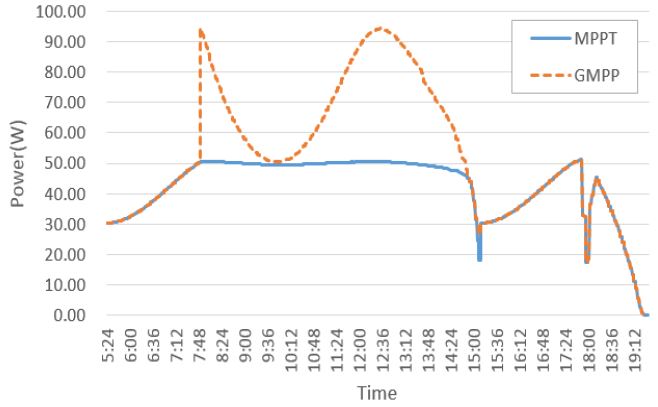
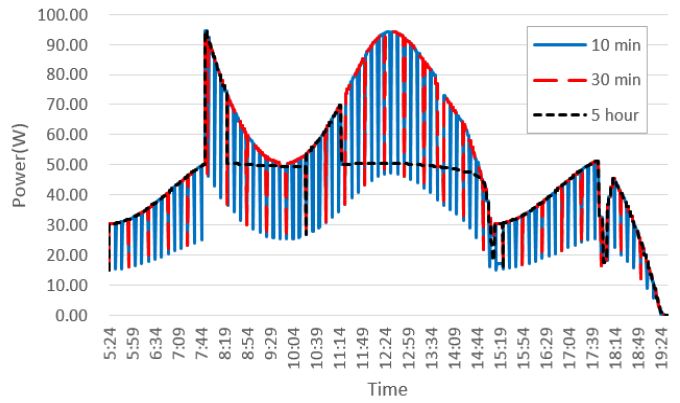
The case of the GMPP has the most ideal power generation. When the MPPST algorithm is applied, searching operation loss and a reduction in power generation efficiency of the GMPP movement during the operation period of the MPPT algorithm exist. Figure 15 is an output graph of the MPPST algorithm according to the searching cycle. The simulation was simulated for a total of 12 cases of the searching cycle.
Figure 14 shows that the MPPST algorithm has lower power generation than the MPPT algorithm during the searching operation, and this is the searching operation loss in the MPPST algorithm.
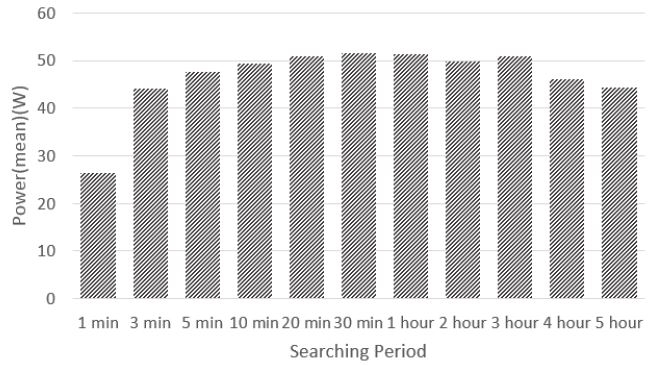
Figure 15 is a graph summarizing the average power generation of the MPPST algorithm according to searching cycle time, and the values are summarized in Table 4.
The searching cycle that has the highest power output is 30 min. If the search cycle is too short, the amount of power loss caused by the searching operation becomes large, and if the searching cycle is too long, power generation loss will occur because of the failure to follow the GMPP properly. In most cases, the power generation efficiency was higher than that of the MPPT algorithm, but the output was lower than that of the MPPT in the 1-min cycle with the shortest search period.
6.Conclusions
The MPPST algorithm increases the power generation efficiency for finding the GMPP through a searching algorithm. In this study, a solar panel model and irradiation model were created. Then, simulation of the MPPST algorithm with different searching periods was performed. When using the existing MPPT algorithm, the average generation was 42.48 W. In a searching period of 30 min, the generator developed 51.62 W and had the highest development efficiency of the MPPST algorithm.
When the power generation efficiency in the GMPP of the most ideal power state was 100%, the MPPT algorithm had an efficiency of 80.21%, and the MPPST algorithm for the 30-min cycle had an efficiency of 97.48%. The MPPST algorithm with a 30-min searching cycle showed an efficiency increase of 17.27% compared with the existing 5-min cycle MPPST algorithm and a 7.4% increase over the 10-min cycle MPPST algorithm.
Acknowledgments
This work was supported by the World Class 300 R&D Program (10050317, Development of eco-friendly Single Point Mooring System with integrated control system operable up to maximum water depth 100 meters) funded by the Small and Medium Business Administration (SNBA, Korea).
References
- I. W. Christopher, and R. Ramesh, “Comparative study of p&o and inc mppt algorithms”, American Journal of Engineering Research, 2(12), p402-408, (2013).
-
K. J. Jo, S. Y. Jung, S. Y. Bae, J. Y. Lee, and J. S. Oh., “A study on the MPPT algorithm for buoy”, Journal of the Korean Society of Marine Engineering, 33(4), p588-594, (2009), (in Korean).
[https://doi.org/10.5916/jkosme.2009.33.4.588]

- N. Belhaouas, M. S. A. Cheikh, A. Malek, and C. Larbes, “Matlab-simulink of photovoltaic system based on a two-diode model simulator with shaded solar cells”, Revue des Energies Renouvelables, 16(1), p65-73, (2013).
-
K. Ishaque, K., Z. Salam, and H. Taheri, “Accurate MATLAB simulink PV system simulator based on a two-diode model”, Journal of Power Electronics, 11(2), p179-187, (2011).
[https://doi.org/10.6113/jpe.2011.11.2.179]

-
H. Patel, and V. Agarwal, “Maximum power point tracking scheme for PV systems operating under partially shaded conditions”, IEEE Transactions on industrial electronics, 55(4), p1689-1698, (2008).
[https://doi.org/10.1109/tie.2008.917118]