1-션트 인버터의 고조파 저감을 위한 새로운 상전류 복원에 관한 연구

1. 서 론

3상 교류 전동기의 토크 제어를 위해 전동기의 자속과 전류에 대해 각각의 크기와 위상을 제어해야 한다. 이때 자속을 기준으로 전류의 방향과 크기를 제어하는데 이러한 방법을 벡터 제어하며 이를 위해 전동기의 상전류의 정보가 필수적으로 요구된다. 상전류 측정방법은 일반적으로 3가지 방법으로 측정한다.

첫 번째 방법은 전류 센서를 이용한 것으로 인버터의 출력단에 전류 센서 2개를 부착하여 서로 다른 2개의 상전류 정보를 획득하고 나머지 1상의 전류는 키르히호프 전류법칙에 의해 구한다. 기본파 성분을 획득할 수 있다는 장점이 있지만 전류 센서의 사용으로 인버터 시스템의 부피가 커지고 가격이 비싸다는 단점이 있다[1][2].

두 번째 방법은 3개의 션트 저항을 이용하여 통해 전류를 획득하는 것으로 인버터 각 암의 하단 스위치 아래에 삽입한 것으로 3-션트 인버터라고 하며 전류 센서를 이용하는 방법보다 인버터의 부피와 가격을 줄일 수 있다. 그러나 영 전압 벡터가 인가 될 경우 전류를 획득하므로 전압 변조 지수가 큰 경우에는 영 전압 벡터의 인가시간이 짧아 정확한 상전류를 획득할 수 없는 경우도 발생한다[3]-[5]. 또한, 3개의 상전류 획득과 관련하여 주변회로에 의해 오프셋이나 스케일 오차로 인해 속도 맥동이 발생할 수 있다[6][7].

마지막으로 세 번째 방법은 직류단의 1개의 션트 저항을 이용하여 전류를 복원하는 것으로 1-션트 인버터라 하며 유효 전압 벡터가 인가될 때, 션트 저항으로 부터 상전류를 획득할 수 있다[8]-[10]. 부피 및 비용 측면에서 이점을 가지고 있으며 상전류를 획득할 때 필요한 회로가 1개 이므로 스케일 오차 등에 따른 문제점이 작다는 것이 장점이 있다. 그러나 1-션트 인버터는 PWM 한 주기 동안 션트 저항을 통해 전류를 샘플링하여 측정 할 수 있는 시간이 제한적이고 출력전압 육각형에서 측정 불가 영역이 넓게 존재하는 문제점이 있다. 이러한 문제점에도 불구하고 최근 산업계에서는 1-션트 인버터의 측정 불가 영역에서 상전류복원을 위한 연구가 활발히 진행되고 있다. 기존의 복원방법들은 션트 저항으로부터 전류를 측정할 때 발생하는 전류 측정 불가 영역은 스위칭 패턴을 변화시키거나 공간 벡터 전압 변조 기법(Space Vector Pulse Width Modulation, SVPWM) 이외의 기법을 사용함으로써 유효 전압 벡터 인가 시간을 확보하여 전류를 추정하였다[8]-[10]. 하지만 변화된 스위칭 패턴과 주입되는 전압의 양에 비례하여 부하에 인가되는 상전류의 전 고조파 (Total Harmonic Distortion, THD)가 높아지는 특성에 따라 기존의 방법들은 상전류에 높은 전 고조파를 포함한다는 문제점을 가지고 있으며 이로 인한 소음도 증가한다. 그러므로 본 논문에서는 기존의 1-션트 인버터의 전류 복원 방법들과 비교, 분석을 통해 높은 전 고조파 특성을 해결하는 방법을 제안하고 시뮬레이션을 통해 검증한다.

2. 1-션트 인버터

2.1 1-션트 저항을 이용한 상전류 획득방법

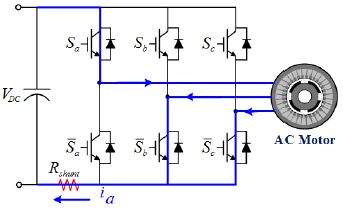
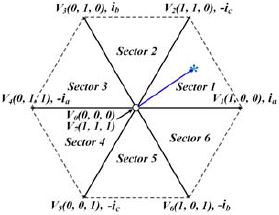
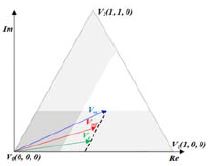
DC단의 션트 저항에 전류가 흐를 때 션트 저항의 양단을 샘플링하여 얻은 전압 값에 옴의 법칙을 이용하여 상전류를 획득한다. 상전류 획득을 위해서는 인버터의 DC단까지 전류 경로가 형성되어야 하며 인버터에 유효 전압 벡터가 인가되어야 한다. Figure 1과 같이 유효 전압 벡터 V₁(100)이 인가될 때는 인버터의 a상 상단 스위치와 b, c상의 하단 스위치가 켜진다. 이 상태에서는 직류단 션트 저항에는 a상 전류가 흐른다. 3상 SVPWM 인버터의 IGBT의 스위칭 조합에 따른 유효 전압 벡터와 획득 가능한 상전류를 출력전압 육각형에 나타내면 Figure 2와 같다. 상단과 하단의 암의 IGBTT의 On/Off 조합에 따라 6개의 유효전압 벡터와 상단-암의 IGBT가 모두 On인 V₇(111)과 하단-암의 IGBT가 모두 On인V₀(000)의 영 전압 벡터가 2개 존재한다.

Figure 1:

Current of DC link when effective vector “1”, “0”, “0” is applied to inverter

Figure 2:

Output voltage vector hexagon of 1-shunt three-phase Inverter

2.2 측정 불가 영역

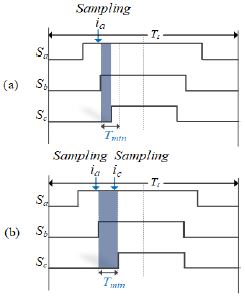
션트저항으로부터 상전류를 획득 시점과 획득 가능한 상전류를 PWM 한 주기에 나타내면 Figure 3과 같다. PWM 반주기를 한 전압 변조 주기하면 PWM 한 주기 T_S는 두전압 변조 주기로 구성되며 Figure 3과 같이 한 스위칭 주기에 2개의 유효 전압 벡터 V₁, V₂가 인가된다. 이 때 션트 저항 양단의 전압을 샘플링하여 2상의 전류를 획득하고, 나머지 1상의 전류는 키르히호프 전류 법칙을 이용하여 구한다. 션트 저항으로부터 정확한 상전류를 획득하기 위해서는 PWM 스위칭에서 유효 전압 벡터가 인가된 시점부터 전류 측정에 필요한 최소한의 시간 T_min이 요구되며 식 (1)과 같이 정의한다.

$\[ T_{\text{min}}=T_{dead}+T_{setting}+T_{A/D} \]$

(1)

Figure 3:

One PWM period of SVPWM method

여기서 T_dead는 인버터의 데드 타임(Dead time), T_setting는 션트전압 안정화 시간, T_A/D는 A/D(Analog to Digital) 샘플링 변환 시간이다.

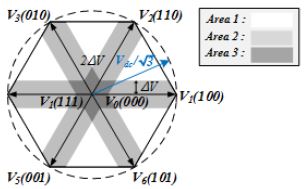
이상적인 PWM 스위칭은 유효 전압 벡터 인가 시간 T_{eff_votlage}가 최소한 T_min보다 커야 정상적인 상전류 측정이 가능하지만 만약 T_{eff_votlage}가 T_min보다 작은 경우 션트 저항으로부터 정확히 상전류를 측정 할 수 없다. 이를 측정 불가 영역이라 하며 복소 공간에 표현하면 Figure 4와 같다. 복소 공간을 3가지의 영역으로 나누면 Area 1는 2 상 전류 모두 측정이 가능한 영역(T_{eff_votlage}≥T_min), Area 2와 Area 3은 1상 전류만 측정이 가능한 영역과 2상 전류 모두 측정이 불가능한 영역(T_{eff_votlage}<T_min)으로 나타낸다.

Figure 4:

Current unmeasurable area in 1-shunt inverter

3. 기존의 상전류 복원방법

3.1 PWM 시프트 방법

PWM 시프트 방법은 한 스위칭 주기 내에서 PWM 스위칭 패턴을 좌, 우 변화에 의해 유효 전압 벡터 인가 시간을 확보하는 방법이다[8]. Figure 5는 PWM 시프트 방법 적용 전ㆍ후를 나타내며 Figure 5 (a)는 1개의 스위칭 주기 내에서 2개의 유효 전압 벡터 중 1개의 인가 시간이 T_min보다 작은 경우의 스위칭 패턴으로 1상의 전류만 션트 저항으로부터 전류를 측정 할 수 있는 경우이다. 그러나 Figure 5 (b)와 같이 PWM 시프트 방법을 적용하여 스위칭 패턴을 이동시켜 2개의 유효전압 인가시간을 T_min이상 되도록 하여 션트 저항으로부터 2상의 전류를 측정할 수 있다. 그리고 나머지 1상의 전류는 키르히호프 전류 법칙을 통해 구할 수 있다. Figure 6는 PWM 시프트 방법을 복소 공간에서 표현한 것으로 지령 전압 벡터 V_ref가 측정 불가 영역 Area2에 인가되고 있다. T_min을 확보하기 위해 V_ref 대신 반 주기 동안은 측정 전압 벡터 V_m를 측정 가능 영역의 경계로 인가하고, 나머지 반 주기 동안에는 보상 전압 벡터 V_c를 인가한다. PWM 시프트 방식은 1주기 동안 1상의 전류만 측정 가능하며 2상 측정이 불가능한 경우 2개의 스위칭 주기가 필요하다. 측정 불가 영역에서도 션트 저항으로부터 2상의 전류의 추정이 용이하지만 2개의 스위칭 패턴의 주기 변화에 의한 전압 왜곡이 커서 고조파가 증가하는 것이 단점이다.

Figure 5:

One PWM period of SVPWM method

Figure 6:

One PWM period of SVPWM method

3.2 MVI(Minimum Voltage Injection) 방법

3.1에서 고조파 증가를 줄이기 위해 스위칭 패턴 변화를 최소화하기 위해 MVI 방법이 제안되었다[9][10].

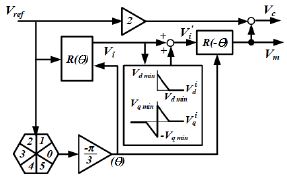
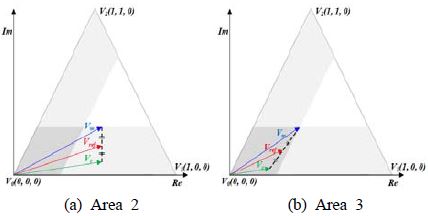
앞서 언급한 것처럼 V_m 와 V_c를 각각 반 주기 동안 인가해야 한다. MVI 방법은 지령 전압 벡터에 최소 주입 전압값을 계산하여 V_m에 합한다. 그 결과 V_ref와 V_m의 차이가 기존의 PWM 시프트 방법을 사용했을 때보다 고조파가 발생이 적다. MVI 방법은 Figure 7과 같으며 V_ref 에 대해 전압 육각형에서 Sector 0으로 회전시켜 V_i을 구하고 이를 d축 전압의 V_{d min}값과 q축 전압의 V_{q min}값을 서로 비교한 후 주입되는 최소 전압값 $$ V_i^{\text{'}}$$을 결정한다. $$ V_i^{\text{'}}$$값은 V_i값에 합하고 다시 역회전을 통해 전류 측정이 가능한 V_m을 구한다. 이 때 V_c는 Figure 7과 같이 V_c=2V_ref-V_m 로 구해진다. Figure 8는 MVI 방법을 복소 공간에서 표현한 것으로 Figure 8 (a)는 한 상의 전류만을 측정 가능한 영역 Area2로 V_ref에 대해 d축의 전압은 인가되지 않고 q축의 전압만 주입되어 V_m와 V_c가 계산되어 인가된다. Figure 8 (b)는 2상의 전류 모두 측정이 불가능한 영역 Area3로 d축과 q축의 전압이 인가되어 V_m와 V_c가 계산되어 2상 모두 측정이 가능한 지점으로 이동된다.

Figure 7:

Control block diagram of MVI method

Figure 8:

MVI method in the complex plane

4. 제안하는 상전류 복원방법

4.1 측정 불가 영역(Area 2)에서 상전류 복원 방법

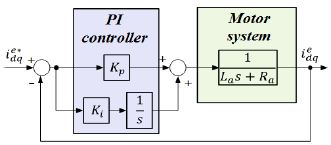
한 상의 전류만 획득 가능한 Area 2에서는 지령 전류를 이용하여 상전류를 추정하는 방법으로서 저역 통과 필터(Low Pass Filter, LPF)를 통과 시켜 얻을 수 있다. 3상 교류 전동기의 속도 제어를 위해 전류 제어가 필요하고 전류 제어기의 경우 Figure 9와 같이 동기 좌표계 d-q축 비례 적분 제어기가 사용된다. 여기서 R_s, L_s, K_p 그리고 K_i는 각각 고정자 저항, 고정자 인덕턴스, 비례 이득 그리고 적분이득이다.

Figure 9:

Block diagram of PI controller and motor system

K_p과 K_i은 식 (2)와 같이 나타낼 수 있다.

$\[ \begin{array}{c}{K}_p=L_a{\omega }_{cc},\hfill \\ K_i=R_a{\omega }_{cc}\hfill \end{array} \]$

(2)

여기서 ω_cc는 동기 좌표계 PI 전류 제어기의 대역폭이다. 이 방법은 d-q축 지령 전류를 이용한 것으로 스위칭 패턴변화나 전압을 인가하지 않고 전류를 복원이 가능하여 기존방법에 비해 고조파 발생이 적다.

4.2 측정 불가 영역(Area 3)에서 상전류 복원 방법

4.2.1 상전류복원을 위한 영역 구분

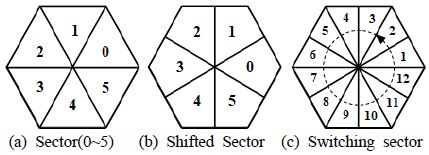
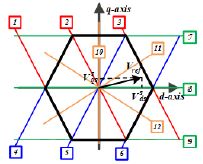
2개의 상전류의 획득 불가능한 Area 3에서 상전류 복원을 위해 최적을 주입할 때 주입되는 전압의 계산을 용이성을 위해 Sector 및 회전된 Sector의 판별이 필요하며 이를 위해 다른 스위칭 조합으로 형성되는 12개의 스위칭 Sector가 요구된다. 이러한 영역들은 Figure 10과 같다. 또한 스위칭 섹터의 구분을 위해 복소 공간상에 존재하는 두 점을 이용하여 Figure 11과 같이 12개의 직선의 방정식을 구한다.

Figure 10:

Sector classification

Figure 11:

Line for sector classification

-60°의 기울기를 가지는 직선의 방정식은 직선 1 ~ 3로 정의하고 +60°의 기울기를 가지는 직선의 방정식은 직선 4~6으로, 0의 기울기를 가지는 직선의 방정식은 직선 7~9로, 나머지 직선의 방정식들을 10~12로 정의한다. Figure 11과 같이 지령 전압 벡터 V_ref가 위치한다면 식 (3)을 동시에 만족할 때 지령 전압 벡터의 위치를 포함할 수 있다.

$\[ \begin{array}{c}\text{직선} 3 :V_{qs}^s\le -\sqrt{3}\left(V_{ds}^s-2/3V_{dc}\right),\hfill \\ \text{직선} 8 :V_{qs}^s\ge 0\hfill \\ \text{직선} 11 :V_{qs}^s\le 1/\sqrt{3}\left(V_{ds}^s\right)\hfill \end{array} \]$

(3)

4.2.2 최적 전압 인가 방법

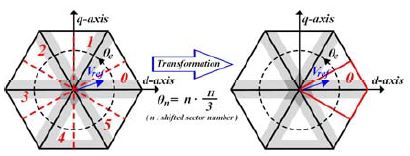
인가하는 전압 계산을 위해 Figure 12와 같이 0~2π로 회전하는 지령 전압 벡터 V_ref를 식 θ_n=n∙π/3(n은 회전된 섹터)으로 회전 변환한다. 지령 전압 벡터가 회전된 섹터 1에 위치하면 θ₁로 회전변환, 회전된 섹터 2에 위치하면 θ₂로 회전 변환한다. θ_n을 이용하여 0~2π로 회전하는 지령 전압 벡터를 –6/π~6/π로 회전시키는 효과를 가지며 인가되는 전압을 계산할 때 회전된 섹터 0에 대해서만 고려하면 된다. 회전된 섹터 0는 d축에 대하여 대칭이고 음의 q축은 d축의 주입 전압의 크기와 같고 부호만 반대이므로 Figure 13과 같이 인가되는 전압의 크기는 양의 q축에 대해서만 고려하면 된다.

Figure 12:

Shifted Sector

Figure 13:

Shifted Sector 0

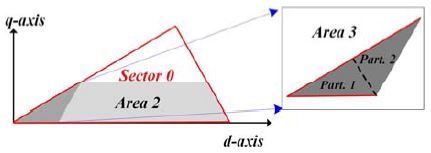
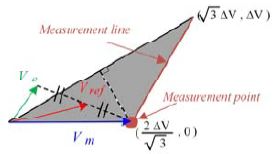
상전류 복원을 위해 필요한 만큼 인가되는 전압 $$ V_{dqs}^i$$을 계산하고 회전 변환 전압 $$ V_{dqs}^t$$에 더해준다. 이 더해준 값을 다시 θ_n=n∙π/3 으로 역변환하면 PWM 한 주기의 첫 번째 전압 변조 주기에 인가되는 측정 전압 벡터V_m가 된다. 두 번째 전압 변조 주기에는 보상 전압 벡터 V_c를 인가해준다. 최적 전압 인가를 통한 상전류 복원을 위해 양의 q축에 대한 회전섹터 0에 대해 Figure 14과 같이 Part. 1과 .2로 구분한다. 지령 전압 벡터 V_ref가 Figure 15와 같이 Part. 1에 위치할 경우 최적 전압을 주입하여 측정 전압 벡터 V_m를 Measurement point로 이동시킨다. 이때 Measurement point는 Area 2의 경계가 된다. 인가 되는 전압 $$ V_{dqs}^i$$는 Measurement point에 해당하는 좌표에서 θ_n으로 회전 변환 전압 $$ V_{dqs}^t$$을 빼주면 구할 수 있으며 d, q축으로 주입되는 전압의 크기는 식 (4)와 같다.

$\[ \begin{array}{c}{V}_{ds}^i=\left(2∆V/\sqrt{3}-V_{ds}^t\right),\hfill \\ V_{qs}^i=-V_{qs}^t\hfill \end{array} \]$

(4)

Figure 14:

Optimal voltage injection method in Part. 1

Figure 15:

Optimal voltage injection method in Part. 2

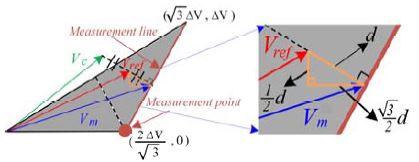
V_ref가 Part. 2에 위치할 때 최적의 전압을 주입하여 V_m를 Measurement line으로 이동 시킨다. 이 경우 Measurement line은 Area 2의 경계로서 2개의 점 $$ \left(2∆V/\sqrt{3},0\right)$$와 $$ \left(\sqrt{3}∆V,∆V\right)$$에 의해 식 (5)와 같이 직선의 방정식으로 표현되며 회전변환 전압 $$ V_{dqs}^t$$ 과의 거리 d는 식 (6)과 같다.

$\[ \left(V_{qs}^t=\sqrt{3}\left(V_{ds}^t-\sqrt{3}∆V\right)+∆V\right. \]$

(5)

$\[ d=\frac{1}{2}\left|\sqrt{3}{V}_{ds}^t-V_{qs}^t-2∆V\right| \]$

(6)

측정 전압 벡터를 Measurement line까지 이동시키기 위해 d축에 $$ \sqrt{3}d/2$$의 전압을 인가하고 q축에 -d/2의 전압을 인가한다. 최적 전압 주입 방법은 Part의 Area3 영역을 작게 구분하여 지령 전압 벡터와 가장 인접한 Measurement line 또는 Measurement point로 측정전압 벡터를 이동시켜 상전류를 복원하는 방법이다. 이 경우 Measurement line 또는 Measurement point는 Area 1 또는 Area 2의 경계가 된다.

5. 시뮬레이션 및 검토

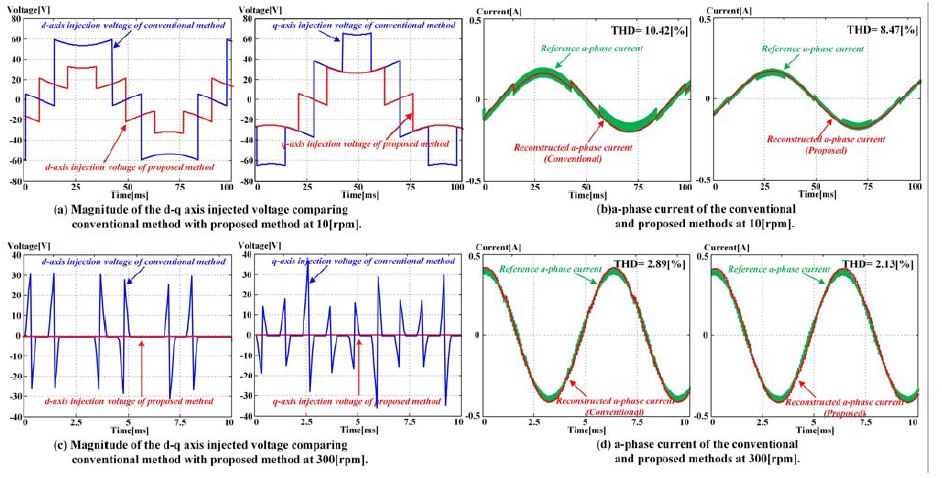
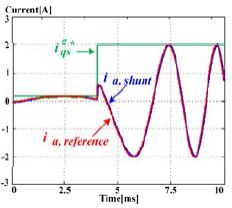
제안된 상전류 복원방법의 성능을 확인하기 위해 시뮬레이션을 통해 검증하였으며 시뮬레이션에 사용된 영구자석 동기전동기(SPMSM)는 가정용 세탁기의 파라미터의 값으로 Table 1과 같다. 시뮬레이션은 30[rpm]과 400[rpm]에서 수행하였고 지령 전압 벡터는 Area 3과 Area 2에 인가 되도록 하였다. 기존의 방법은 측정 전압 벡터를 위상 전류의 복원을 위해 항상 Area 1에 인가한다[9][10]. 그러나 제안된 방법은 Area 3의 경계 근처에 인가되어 복원한다. Figure 16 (a)와 Figure 16 (b)는 지령 전압 벡터가 Area 3에서 30[rpm]으로 운전되는 것으로 기존의 방법과 제안한 방법을 이용하여 d-q축의 인가 전압량과 상전류 복원을 위한 인가 전류량을 나타내었다. Figure 16 (b)에서와 같이 제안한 방법의 인가 전류량이 작아 THD를 감소함을 알 수 있다. Figure 16 (c)와 Figure 16 (d)는 400[rpm]에서의 운전으로 지령 전압 벡터가 Area 2에 인가된 경우로 (c)는 d-q축의 인가 전압량, (d)는 인가 전류량으로 기존의 방법은 전압 인가를 통해 위상 전류를 복원하지만 제안한 방법은 지령 전류를 이용하여 위상전류를 복원한다. Figure 16 (d)도 인가 전류량이 적어 10[rpm]의 경우와 동일하게 THD가 감소한 것을 알 수 있다. Figure 17은 제안한 방법을 이용하여 운전속도가 30[rpm]에서 400[rpm]으로 증가 할 때 과도 상태 및 정상 상태 전류 파형을 나타낸 것으로 션트 저항을 이용하여 복원한 상전류와 전류센서의 상전류 신호가 거의 동일한 것을 알 수 있다.

Table 1:

Parameters used in simulation

Figure 16:

Simulation results comparing with the conventional and proposed methods

Figure 17:

Optimal voltage injection method in Part. 2

6. 결 론

본 논문에서는 가격과 부피를 고려한 1-션트 인버터에 고조파 저감을 위한 3상 전류의 복원방법을 제안한다.

첫째 상전류 복원 알고리즘을 적용을 위해 섹터, 회전된 섹터 그리고 스위칭 섹터로 구분하고 영역구분을 위해 직선방정식을 이용한다. 출력전압 즉 지령 전압 벡터가 출력전압 육각형에 위치하면 영역의 각 스위칭 상태에서 유효전압 인가 시간과 T_min을 비교하여 해당영역의 Area을 결정한다.

둘째, Area 1에서는 지령 전압 벡터에 따라 션트 저항으로부터 비교적 2상 또는 3상 전류를 용이하게 획득할 수 있다. 그러나 한 상전류가 획득 가능한 Area 2에서 기존의 PWM 시프트 또는 전압 인가를 하지 않고 전동기의 전기적 모델링을 사용하여 PI 제어기로부터 지령전류를 추정하여 위상 전류를 복원한다.

셋째, 2상전류가 획득 불가능한 Area 3에서는 최적의 전압 인가를 위해 Part. 1과 Part. 2로 구분하고 측정 전압 벡터를 지령 전압 벡터와 가장 인접한 Area 1 또는 Area 2의 경계로 이동시켜 상전류를 복원한다.

제안하는 방법은 기존의 방법과 비교하여 인가되는 전압의 양이 작으므로 정확도 및 THD 특성의 우수성을 확인하였으며 시뮬레이션 결과를 통해 제안된 방법의 유효성을 검증하였다.

References

• L. Jarzebowicz, “Error analysis of calculating average d-q current components using regular sampling and park transformation in FOC drives”, 2014 International Conference and Exposition on Electrical and Power Engineering (EPE 2014), p901-905, (2014). [https://doi.org/10.1109/icepe.2014.6970042]
• V. Blasko, V. Kaura, and W. Niewiadomski, “Sampling of discontinuous voltage and current signals in electrical drives: A system approach”, IEEE Transactions on Industry Applications, vol. 34(no. 5), p1123-1130, (1998). [https://doi.org/10.1109/28.720453]
• S. H. Jung, and I. Ha, “Carrier signal injection method in three shunt sensing inverter for sensorless AC machine drive”, IEEE Energy Conversion Congress and Exposition (ECCE), p4154-4161, (2014). [https://doi.org/10.1109/ecce.2014.6953967]
• D. Y. Kim, J. H. Lee, T. K. Lee, and C. Y. Won, “Phase current sensing method using three shunt resistor for AC motor drive”, 2012 IEEE Vehicle Power and Propulsion Conference, p78-82, (2012). [https://doi.org/10.1109/vppc.2012.6422566]
• E. W. Lee, S. H. Byun, C. O. Hong, C. S. Yang, and J. B. Kim, “Time-based current detection method with three shunt resistors in the 3-phase PWM inverter”, Industrial Electronics Society, IECON 2013 - 39th Annual Conference of the IEEE, p1380-1385, (2013). [https://doi.org/10.1109/iecon.2013.6699334]
• D. W. Chung, and S. K. Sul, “Analysis and compensation of current measurement error in vector-controlled AC motor drives”, IEEE Transactions on Industry Applications, vol. 34(no. 5), p340-345, (1998).
• W. S. Im, S. H. Hwang, J. M. Kim, and J. H. Choi, “Analysis and compensation of current measurement errors in a doubly fed induction generator”, 2009 IEEE Energy Conversion Congress and Exposition, p1713-1719, (2009). [https://doi.org/10.1109/ecce.2009.5316170]
• Y. Gu, F. Ni, D. Yang, and H. Liu, “Switching-state phase shift method for three-phase-current reconstruction with a single DC-link current sensor”, IEEE Transactions on Industrial Electronics, vol. 58(no. 11), p5186-5194, (2011).
• J. I. Ha, “Voltage injection method for three-phase current reconstruction in PWM inverters using a single sensor”, IEEE Transactions on Power Electronics, vol. 24(no. 3), p767-775, (2009).
• H. J. Shin, and J. I. Ha, “Phase current reconstructions from DC-Link currents in three-phase three-level PWM inverters”, IEEE Transactions on Power Electronics, vol. 29(no. 2), p582-593, (2014).