다양한 TSR변화에 따른 1MW급 조류발전 터빈 블레이드 형상설계와 출력성능 예측
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문에서는 일반적으로 블레이드 공력설계와 출력 성능해석에 활용되고 있는 날개요소운동량이론을 이용하여 1MW급 수평축 조류터빈 블레이드 기본형상을 설계하였다. 기본형상은 NREL S814 에어포일을 적용한 3엽 블레이드이다. 조류터빈 블레이드는 해양환경 특성상 해류와 수압 등에서 운전되므로 형상 설계 시 신중히 고려되어야 한다. 본 블레이드 형상의 유동특성 및 출력성능을 비교 검토하기 위해 주속비 별로 CFD을 수행하였으며 블레이드의 각각의 국부위치에서 압력계수와 출력성능을 검토하였다. CFD에 의한 기계적 최대출력계수는 설계 주속비 5의 조건에서 48%로 나타났다.
Abstract
We designed the basic shape of a 1-MW horizontal-axis tidal-current turbine blade utilized for blade element momentum theory, which has been used generally for aerodynamic design and power performance analysis. The basic shape is a three-blade applied to NREL S814 airfoil. Tidal current turbine blades are operated by ocean current and water pressure because of the nature the marine environment and the environment should be discretely considered when designing the shape. To compare the flow characteristics and power performance of the present blade shape, computational fluid dynamics CFD analysis was performed according to the blade tip speed ratio (TSR), and the pressure coefficient and power performance were examined at each local position of the blade. The mechanical maximum power coefficient due to CFD was 48% under the condition of TSR 5.
Keywords:
Horizontal axis tidal turbine, Blade element momentum theory, Computational fluid dynamics, Tip speed ratio, Power coefficient키워드:
수평축 조류터빈, 날개요소운동량이론, 전산유체역학, 주속비, 출력계수1. 서 론
전 세계적으로 인류의 주 에너지원인 화석자원의 고갈과 더불어 온실가스의 배출 급증에 따른 지구온난화가 가속화됨에 따라 친환경적인 신재생에너지에 대한 관심이 커지고 있다. 현 정부는 탈 원전을 위한 방안으로 신재생에너지를 통한 전력 생산 비율을 2030년까지 20%까지 끌어올리겠다는 “신재생 3020“ 정책을 발표 하였다[1]. 하지만 대한민국 실정상 신재생에너지 발전 설비 용량이 턱없이 부족한 것이 현실이다. 산업통상자원부에서는 신재생에너지 발전 비중 20% 달성을 위해서는 53GW 규모의 신규 설비가 필요하다고 밝혔으며, 태양광, 풍력을 80% 넘는 수준으로 보급해 선진국 수준의 신재생 에너지 생태계를 구축해야 한다고 하였으나 현실적으로 태양광과 풍력을 80% 넘는 수준으로 보급하기에는 많은 제약이 따라 해양에너지에 대한 관심이 집중되고 있다.
해양에서 이용 가능한 에너지원으로 조석, 조류, 해류, 파랑, 해상풍, 수온차 등이 있지만 그 중에서 우리나라는 세계적으로 보기 드문 조류발전의 적지이며, 국내 연안에는 약 6GW 이상의 조류에너지가 부존되어 있는 것으로 추정되고 있다[3].
특히 우리나라의 서남해안은 조류에너지 여건이 아주 좋은 것으로 평가되고 있고, 부존량도 많아 대체에너지로써 개발가치가 높다. 진도 울돌목, 장죽수도, 맹골수도, 완도, 횡간수도 등 다도해의 빠른 조류 자원은 세계적인 조류발전 최적지로 우리나라 해양에너지 자원의 보고이다. Table 1은 서남해역의 조류에너지 부존량과 개발가능한 자원에 대해 나타내고 있다. 조류발전 터빈은 터빈 축과 유동의 방향에 따라 수평축 조류터빈(Horizontal Axis Tidal Turbine, HATT)와 수직축 조류터빈(Vertical Axis Turbine, VATT)의 두 종류로 나눌 수 있다. 수평축 조류터빈은 일반적으로 수직축 조류터빈보다 높은 발전 효율을 보여주기 때문에, 설계에 어려움이 있더라도 수평축 조류터빈의 효율을 예측하거나 계측하기 위한 실험적인 연구들이 다수 이루어졌다[4].
조류발전은 개발 역사가 짧아 국내외 기술력의 차이가 크지 않고 상당부분 기존의 풍력에서 사용하는 개념을 그대로 사용하고 있기 때문에 유체의 흐름, 효율, 캐비테이션, 해수의 특성과 같은 측면을 고려한 여러 가지 개선의 여지가 많다.
본 연구에서는 1MW급 수평축 터빈에 대해 다양한 성능해석을 수행하고자 한다. 이를 위해 날개요소운동량이론으로 개발된 설계기법을 이용하여 1MW급 조류발전 터빈 블레이드를 설계하였고 성능 평가를 목적으로 CFD를 이용한 수치해석 결과를 바탕으로 블레이드 각각의 국부위치에서의 압력계수 및 출력성능 등을 검토하였으며 또한 표면유선 및 로터 주변 3차원 유동특성을 고찰하고 주속비(TSR)에 따른 성능해석을 수행하였다.
2. 수평축 조류발전 터빈 블레이드 설계
2.1 에어포일 선정
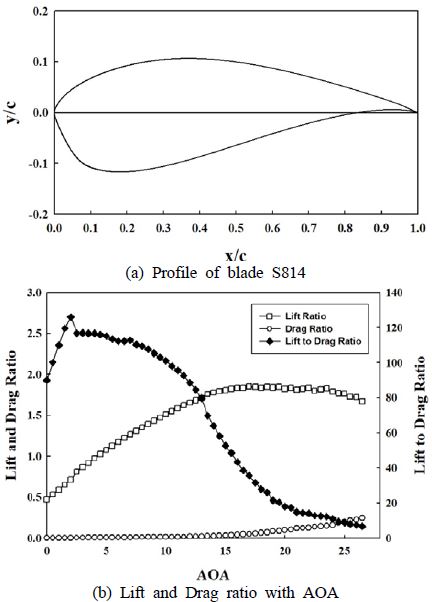
조류발전 터빈의 블레이드가 높은 에너지밀도의 환경에서 운전 될 경우 루트부의 구조안정성이 문제 될 수 있고 실속 받음각 이후의 공력성능 변화가 매우 완만한 특성을 보이는 블레이드를 선정하기 위해 NREL S814 에어포일을 선정하였다. S814는 구조설계에 유리하며 비교적 안정적 출력성능확보가 가능한 에어포일 시리즈를 변화되는 천이구간에서 형상변화를 최소화하기 위한 목적으로 에어포일을 선정하였다[5].
Figure 1은 S814 에어포일과 X-Foil[6]에 의해 계산된 양력계수와 양항비 분포를 보이고 있다. 정확한 에어포일의 공력성능을 예측하기 위해서는 블레이드 국부 위치에서의 에어포일 공력특성을 양력계수와 양항비로 나타낼 필요성이 있으며, 양항비가 높게 결정될 수 있도록 하는 점이 우수한 출력성능 확보를 위해 중요하다[7].
이 논문에서 선정한 S814 에어포일은 레이놀즈 수 Re = 2,200,000 영역에서 받음각 α = 2deg. 일 때 최대 양항비(CL/CD)가 125.9로 높은 값을 나타내고 있으며, 받음각 α = 0.5~10deg. 범위에서 100 이상의 높은 양항비를 나타내고 있으므로 전체적으로 상당히 우수한 성능을 가지는 블레이드 설계가 되었다고 판단된다.
2.2 조류발전 터빈 블레이드 설계
Table 1의 서남해안 해역의 조류 평균속도를 참고하여 설계점 운전조건에 맞추어 결정해야 할 필요성이 있으므로 평균 유속을 약 2.5m/s로 설계하였다. 설계점 유속의 경우 출력 P는 식 (1)과 같이 나타낼 수 있으며, 유입유속의 3승에 비례하기 때문에 식 (2)로 정의되는 주속비 λ = 6 에서 최대출력을 얻을 수 있도록 설계하였다.
| (1) |
| (2) |
여기서, ρ는 물의 밀도, A는 유속면적, V∞는 유입속도이다.
블레이드의 최적설계를 위하여 날개요소 운동량 이론을 적용하여 설계하였으며, Figure 2는 1MW급 수평축 조류터빈 블레이드의 외형도를 나타내고 있으며, Table 2, Table 3는 공력 설계된 블레이드의 제원과 계산결과를 나타내고 있다.
3. CFD에 의한 출력성능 해석
3.1 계산격자 및 수치해석 조건
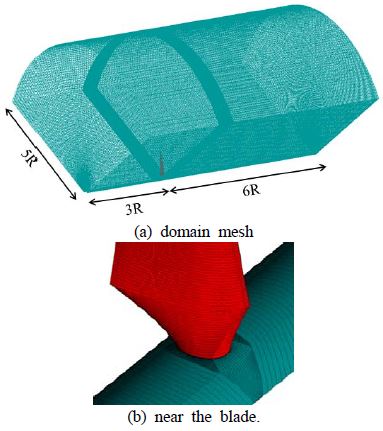
Figure 3은 본 연구에서 설계된 1MW 수평축 조류발전 터빈 블레이드에 대한 수치해석을 위하여 ICEM CFD로 블레이드 및 전체 유동장에 대한 계산격자를 보이고 있다. 계산 영역은 흐름의 입구방향으로 블레이드 반경의 3배 만큼의 거리와 출구방향으로 7배 만큼의 거리 그리고 터빈 높이 방향으로는 5배 만큼의 여유를 두어 구성하였고 계산격자에 사용된 node의 수는 약 900만개이며 ICEM CFD를 이용하여 육면체(Hexahedron)격자를 이용하여 구성하였으며 계산결과의 수렴에 필요한 안정도와 정확도를 높였다[8].
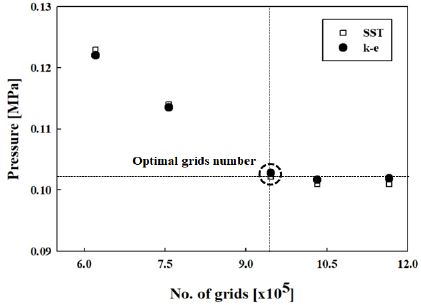
블레이드 표면에서 발생하는 실속에 의한 복잡한 유동흐름을 잘 예측하기 위하여 블레이드 표면 주변은 O-grid를 사용하여 블레이드 주위의 유도장보다 격자밀도가 높게 구성하였으며, 계산의 효율성을 고려하여 블레이드 외부는 H-grid 격자로 구성하였다. 유동해석은 상용코드인 ANSYS CFX ver.18을 사용하였고, 유동박리 현상이 잘 발생하는 유동장의 해석에서 블레이드의 실속현상과 같이 복잡한 유동을 파악하기 위하여 난류모델은 k-ω SST를 사용하였다[9]. k-ω SST 난류모델의 벽면에서 첫 번째 node까지의 무차원 거리인 y+ 는 5이하의 값을 유지하였으며 정상상태계산을 통한 해석을 수행하였고 연속방정식과 운동량 방정식을 하나의 방정식 집합으로 묶어 계산을 수행하는 방법을 사용하였다. 수치모델의 효율성 확보를 위하여 격자의존성시험을 수행하였다. 두 종류의 난류모델을 사용한 격자의존성시험 결과는 Figure 4에 나타내었다. 그림에서 알 수 있듯이, 격자수가 약 900만개 이상일 때 격자의존성이 사라짐을 확인할 수 있었다.
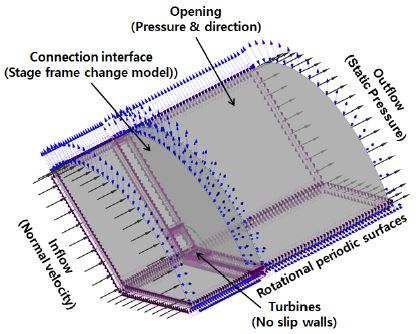
Table 4와 같이 주속비 변화에 따라 주기(periodic)경계조건으로 처리된 단일 블레이드에 대해 수행하였으며, 입구 경계조건으로는 입구에 균일 속도유입조건을 주었고 출구에는 평균정압조건을 설정하였으며 블레이드 표면은 점착조건(no-slip walls)을 적용하였으며, 3개의 블레이드 중 1개의 블레이드에 해당하는 120° 주기적 경계 조건(Rotational periodic boundary condition)을 적용하였으며, 유동영역이 Figure 5와 같이 모델링 되었다.
4. 해석결과
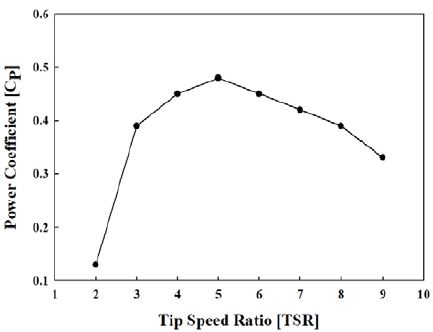
Figure 6은 1MW급 수평축 조류터빈 로터 블레이드에 대한 수치해석 결과로서 출력계수(Cp)에 의한 성능곡선을 주속비 변화에 따라 나타낸 것이다. 주속비 4~7의 구간에서 출력계수(Cp)가 0.4 이상으로 나타났으며, 출력계수의 최대값은 주속비가 5인 구간에서 약 0.48로 계산되었다.
주속비 5이하의 영역에서는 주속비 정의에 따라 로터 블레이드 상류로부터 접근하는 유속의 범위가 설계 출력이 발생하는 유속 범위보다 높은 값을 가지므로 블레이드 전연으로 유입되는 상대유입각도는 증가하고, 동시에 실속각 이상으로 받음각이 증가하면서 급격한 실속한 의한 공력특성 저하가 예상된다. 또한 주속비 5이상의 영역에서는 입구 유속이 설계 출력을 내는 범위보다 감소함에 따라 상대적으로 블레이드 전체 영역에 걸쳐 낮은 범위의 받음각이 형성되어 받음각의 범위가 낮아짐에 따라 익형 공력특성이 저하되므로 출력계수은 점점 낮아지는 경향을 보인다.
Figure 7, Figure 8은 수치해석에 의한 로터 블레이드의 공력특성을 검토하기 위하여 블레이드 압력면(pressure side)과 부압면(suction side)사이의 압력 차이를 압력계수(Cp)값을 이용하여 블레이드 반경방향 국소반경비 및 주속비에 따라 정량적으로 비교 하였다. 압력계수는 식 (3)[10]을 이용하였다.
| (3) |
여기서 p와 p∞는 로터 블레이드 표면과 유동장 유입 측의 정압을 나타내고, ρ∞는 유입 측 흐름의 물의 밀도, r은 로터 블레이드 해당 스팬위치에 대한 블레이드 국소반경방향의 거리, ω는 로터 블레이드의 회전 각속도이다.
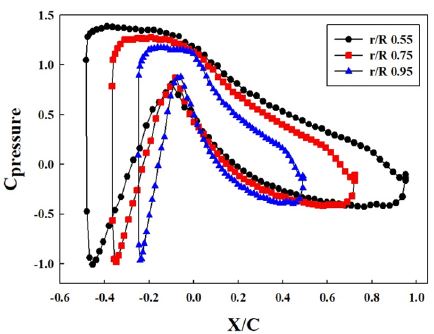
Figure 7은 주속비 5의 블레이드 반경방향 각 국소 반경비에서의 압력계수를 나타내고 있다. 단면 r/R=0.55~0.95 의 압력계수 분포는 거의 비슷한 형태를 보이고 있다. 이는 블레이드 전체에 최대양항비의 받음각으로 인해 우수한 출력성능으로 나타 내어 진다.
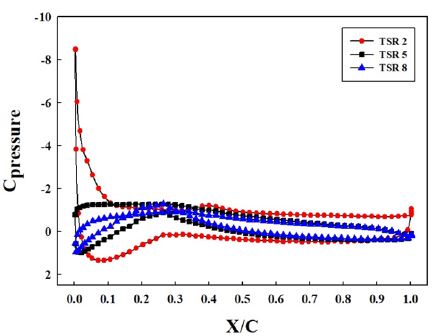
Figure 8은 블레이드 설계에서 반경방향 국소반경비 r/R=0.75 부근의 주속비 2~8의 압력계수를 나타내었다. 주속비 2에서 블레이드 압력면과 부압면 사이 압력계수 전체 면적이 가장 넓게 나타나고 있지만, 주속비가 설계점보다 낮을 경우, 블레이드 상류로부터 접근하는 유속의 범위가 설계 출력이 발생하는 유속 범위보다 높은 값을 가지므로 블레이드 전연으로 유입되는 상대 유입각도의 증가에 따라 급격한 실속에 의한 공력특성의 저하가 예상된다.
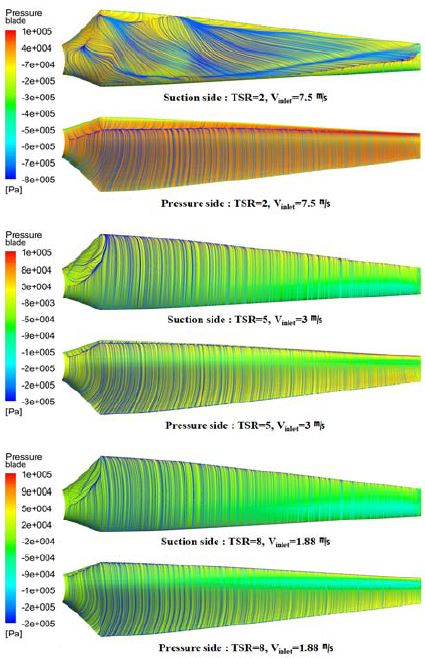
Figure 9는 주속비 변화에 따른 수평축 조류 터빈 블레이드 압력면 및 부압면의 표면 압력 및 유선분포 해석결과를 나타내고 있다.
압력면에서의 표면유선분포는 대부분의 조건에서 상대적으로 균일한 분포의 부착류(attached flow)가 형성되고 있으나, 부압면의 경우 주속비(TSR)=2는 전 범위에 걸쳐 복잡한 형태의 표면유선이 형성 되고 있다. 블레이드 속도는 고정인 반면 유체의 유입속도가 증가함으로 인해 받음각 변화가 크게 발생하여 부압면에서의 깊은 실속이 발행되었기 때문이며, 이로 인해 출력 및 효율저하의 주된 원인이 된다.
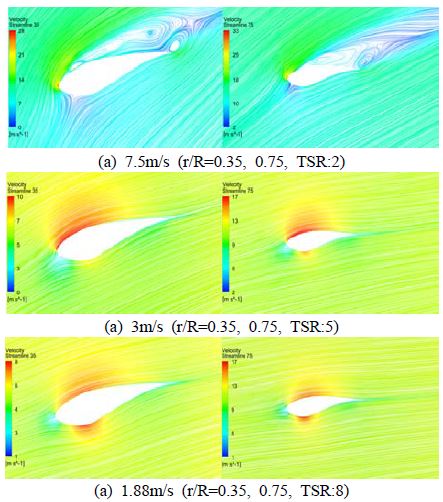
Figure 10는 허브로부터 스팬방향으로의 국부위치 r/R = 0.35인 단면과, 높은 동력이 발생하는 단면인 r/R=0.75단면을 비교하여 입구 유속변화에 따른 유동특성을 나타내었다. 입구 유속이 1.88m/s와 3m/s은 최대양항비의 받음각보다 적은 받음각으로 인하여 익형 전체에 부착류(attached flow)가 형성하여 유동이 빠른 속도로 익형을 통과하고 있어 압력차가 효율적으로 발생함을 확인 할 수 있다. 그러나 입구 유속이 7.5m/s인 경우 최대양항비의 받음각보다 큰 받음각으로 인해 블레이드 후연(trailing edge)에 실속이 발생되어지는 것을 확인할 수 있다. 터빈 블레이드에서의 실속현상은 블레이드에 작용하는 양력을 감소시키고 항력을 증가시키게 되어 터빈의 출력에 영향을 미치게 된다.
5. 결 론
본 연구에서는 날개요소운동량 이론을 적용하여 수평축 조류터빈 블레이드 설계를 수행하였고, NREL S814 에어포일을 이용한 1MW급 조류발전 터빈 블레이드 형상설계에 대한 성능해석을 수행하여 다음과 같은 결론을 얻었다.
- (1) 날개요소운동량이론을 적용하여 1MW급 수평축 조류발전 터빈 블레이드를 설계하였으며, 성능해석 결과에 의한 주속비 5에서 출력계수 Cp=0.48의 최대값을 도출할 수 있었다. 다양한 설계 변수로 인해 설계점인 주속비 6보다 5에서 더 출력계수가 높게 발생하는 것을 확인하였다.
- (2) 조류발전 터빈 블레이드의 수치해석 결과로부터 주속비 5일 때 반경방향 국소반경비 단면 r/R=0.55~0.95의 압력계수 분포는 비슷한 경향을 나타내었으며 이런 현상은 블레이드 전체의 최대양항비의 받음각으로 인해 우수한 출력성능이 발생하는 것을 확인하였다.
- (3) 부압면의 경우 주속비 2일 때 블레이드 전 범위에 걸쳐 복잡한 형태의 표면유선이 형성되었으며 블레이드 속도는 고정인 반면에 유체의 유입속도가 증가함으로 인해 받음각 변화가 크게 발생하였다. 그로인해 흡입 면에서 깊은 실속으로 출력 및 효율저하를 확인하였다.
References
- Ministry of Trade, Industry and Energy, “Renewable Energy 3020 Implementation plan”, (2017), (in Korean).
-
D. S. Byun, E. H. Deirdre, and W. J. Jeong, “Tidal current energy resources off the south and west coasts of Korea: Preliminary observation-derived estimates”, Energies 2013, vol. 6(no. 2), p556-578, (2013).
[https://doi.org/10.3390/en6020566]

- Korea Institute of Ocean Science&Technology, “Development of utilization technique for ocean energy (I): Tide tidal current energy”, Ministry of Oceans and Fisheries Project Report No. BSPM 00078-00-1347-2, (2001).
-
M, H Kim, Y, T Kim, and Y, H Lee, “A study on the performance estimation and shape design of a counter-rotating tidal current turbine”, Journal of The Korean Society of Marine Environment & Safety, vol. 20(no. 5), p586-592, (2014), (in Korean).
[https://doi.org/10.7837/kosomes.2014.20.5.586]

-
J. H. Jung, and B. S. Kim, “Rotor-blade shape design and power-performance analysis for horizontal-axis tidal turbine using CFD”, Transaction of the Korea Society of Mechanical Engineers-B, vol. 39(no. 8), p661-668, (2015), (in Korean).
[https://doi.org/10.3795/ksme-b.2015.39.8.661]

- http://web.mit.edu/drela/Public/web/xfoil/, Accessed April 15, 2018.
- B. S. Kim, A Study on the Optimum Blade Design and the Aerodynamic Performance Analysis for the Horizontal Axis Wind Turbines, Ph.D. Dissertation, Department of Mechanical Engineering, Korea Maritime and Ocean University, Korea, (2005), (in Korean).
- N. J. Lee, I. C. Kim, B. S. Hyun, and Y. H. Lee, “Comparison between CFD and Model experiments of a counter-rotating tidal current turbine by variable parameter”, Proceedings of the KFMA Annual Metting, p99-100, (2014), (in Korean).
-
J. M. Janiszewska, R. R. Ramsay, M. J. Hoffmann, and G. M. Gregorek, “Effects of Grit Roughness and Pitch Oscillations on the S814 Airfoil”, NREL/TP-442-8161, (1999).
[https://doi.org/10.2172/273772]

-
J. Y. Lee, N. J. Choi, H. Y. Yoon, and Y. D. Choi, “Design and flow analysis on the 1KW class horizontal axis wind turbin rotor blade for use in southwest islands region”, Journal of Fluid Machinery, vol. 15(no. 3), p5-11, (2012), (in Korean).
[https://doi.org/10.5293/kfma.2012.15.3.005]