적합성형조건을 이용한 단일과정 수평식 링 압연공정 설계

1. 서 론

링 압연공정은 이음매가 없는 고강도 링 제품을 제조하기 위한 소성가공공정이다. 정형성형(Net shape forming)이 가능하며, 재료 회수율이 매우 높아 우수한 생산성을 가진다. 또한 동일한 제품을 제조할 수 있는 링 단조 및 주조 공정과 비교하면, 제작 시간이 짧고 재료비용이 절감되며 가공 오차를 감소시킬 수 있다. 특히 결정립 유동선이 원주방향으로 끊기지 않고 연속적으로 형성되므로 내·외압에 대한 저항성이 높은 우수한 품질의 제품을 제조할 수 있는 장점이 있다[1][2].

링 압연공정은 주로 발전설비, 화학 플랜트, 가스터빈 및 제트엔진용 링 부품 등 다양한 분야의 부품 제조에 사용되고 있다. 최근 그린에너지 정책과 신재생에너지 개발에 대한 관심이 증가되어 풍력발전용 대형 링 구조부품의 수요가 점차 증가하고 있다. 링 구조부품은 국내의 몇몇 업체에 국한되어 제조되고 있으며, 새로운 형상의 링 부품 제조 시 관리자의 경험과 판단에 의존함으로써 높은 초기 비용과 생산 시간이 소요된다. 또한 최종 제품의 치수정밀도 및 기계적 특성의 신뢰성 확보가 매우 어렵다.

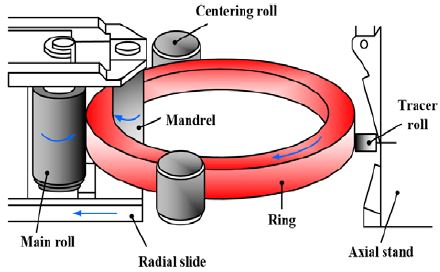
대표적인 점진적 성형공정인 링 압연공정의 제조장비로는 수직식, 수평식 및 다중 맨드렐 링 압연기 등 다양한 종류가 있다. 수평식 장비는 맨드렐에 의한 원주방향의 성형만을 수행하는 단일과정 링 압연기이며, Figure 1에 나타내었다. 장비의 구성은 링 블랭크에 토크를 전달하여 원주방향으로 이송시키는 구동 롤(Main roll), 공회전하면서 소재를 반경방향으로 성형하중을 가하는 맨드렐(Mandrel), 공정 안정성을 높이기 위한 센터링 롤(Centering roll) 등으로 이루어져 있다. 링 블랭크를 구동 롤과 맨드렐 사이에 위치시킨 후 구동 롤을 회전시키면서 맨드렐로 압축력을 가하면 롤 간의 거리가 좁아지면서 링 블랭크의 두께가 얇아지게 된다. 초기 소재의 체적은 소성변형을 받는 동안 일정하므로 링 블랭크의 두께가 얇아지는 것은 링 직경이 증가됨으로써 보상된다.

Figure 1:

Schematic illustration of pure-radial ring rolling machine

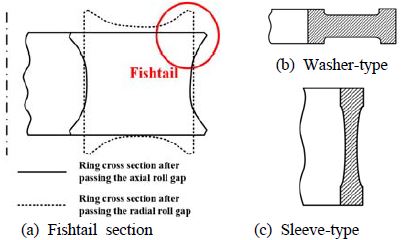
Figure 2에 링 압연공정 중 발생되는 대표적인 형상 결함인 어미 현상(Fishtail)을 나타내었다. 맨드렐의 이송속도는 링 퍼짐량을 변화시키고 어미 결함을 발생시켜 링의 확장에 영향을 미친다. 어미 결함은 최종 제품의 치수정밀도를 감소시키고 더 나아가 링 미세조직의 비균질성 및 크랙 발생을 촉진시킨다[3].

Figure 2:

Shape defects in ring rolling process

실험 및 수치 해석적 방법 등을 통하여 링 압연공정의 특성을 이해하고 어미 결함을 최소화하기 위한 공정 설계 연구가 국내·외 대학과 연구소에서 이루어졌다. J. B. Hawkyard et al. [4]은 R. Hill [5]의 압입 압력 및 소성영역의 평균 두께와 길이의 비를 이용하여 링의 접촉과 롤 하중 및 토크를 예측하고 실험 결과와 비교하였다. A. G. Mamalis et al. [6]은 평면 링과 T자형 형상 링 압연공정의 퍼짐과 재료유동에 대하여 연구하였다. H. Lin et al. [7]은 기존 연구들을 정리하여 맨드렐의 극한 이송속도를 제안하였다. L. Guo et al. [8]은 링 외경증가속도를 기준으로 롤 극한 이송속도를 제시하여 링 압연공정에서의 안정영역을 제시하였다. 최근 K. H. Lee et al. [9]은 R. Hill [5]과 L. Guo et al. [8]의 이론을 결합하여 이중과정 수평식 링 압연공정에서의 개선된 적합성형조건을 개발하였다.

본 연구의 목적은 단일과정 링 압연공정의 제어 알고리즘을 제시하고 어미 결함을 최소화하는 공정 설계를 수행하는 것이다. 마찰을 고려한 평면 변형-압입공정의 슬립라인 이론 및 힘의 평형방정식에 기반으로 한 적합성형조건이 정의되었으며 이를 적용하여 맨드렐의 최소 및 최대 이송속도를 설정하였다. 제안된 적합성형조건을 이용한 공정설계의 유효성은 3차원 유한요소해석을 통해 검증되었고 맨드렐의 이송속도가 링 제품의 형상, 유효변형률 및 온도 분포에 미치는 영향을 정량적으로 평가하였다.

2. 단일과정 수평식 링 압연공정 설계

2.2 적합성형조건

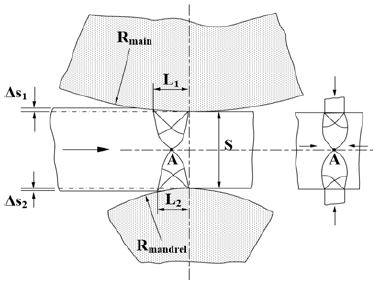
링 압연공정 시 소재의 소성변형영역의 변화 및 어미 결함 발생은 압하량(∆S) 혹은 압하속도(V_mandrel)와 밀접한 관계가 있다. 구동 롤의 1회전 당 맨드렐의 압하량이 너무 작으면 Figure 3에 나타낸 롤과 링의 접촉부(L₁, L₂) 근처에서만 소성영역이 발생하게 된다. 그 결과 소성영역이 링 두께의 중심부(A)까지 충분히 침투되지 못하여 링 외경은 팽창하지 못하고 어미 결함이 발생하게 된다. 링 두께 전반에 걸쳐 소성영역을 발생시키기 위해서는 맨드렐이 최소 압하량 이상으로 압입되어야 한다. 마찰을 고려한 평면 변형-압입공정의 슬립라인 이론 및 힘의 평형방정식에 기초를 하여 구동 롤 1회전 당 맨드렐 최소 압하량(∆S_min,) 및 최대 압하량(∆S_max,)을 적용하는 연구가 진행되었다[9].

Figure 3:

Assumed field for indentation in roll gap [6]

$\[ ∆S_{\text{min}}=1\times {10}^{-2}{\left(R_i-r_i\right)}^2\cdot \left(\frac{1}{R_{main}}+\frac{1}{R_{mandrel}}+\frac{1}{R_i}+\frac{1}{r_i}\right) \]$

(10)

$\[ ∆S_{\text{max}}=\frac{2{\left(\text{arctan}\mu \right)}^2{R}_{main}}{\left(1+R_{main}/R_{mandrel}\right)}\cdot \left(\frac{1}{R_{main}}+\frac{1}{R_{mandrel}}+\frac{1}{R_i}+\frac{1}{r_i}\right) \]$

(11)

맨드렐의 이송속도는 구동 롤이 1회전할 때 소요시간동안 맨드렐의 압하량으로 정의되었으며, 맨드렐 최소 이송속도(∆V_min,) 및 최대 이송속도(∆V_max,)는 다음과 같다. 단일과정 수평식 링 압연공정에서 결함을 최소화할 수 있는 적합성형조건은 아래 식 (12)와 같다.

$\[ {\mathrm{V}}_{\text{min}}\le V_{mandrel}\le V_{\text{max}} \]$

(12)

$\[ V_{\text{min}}=1\times {10}^{-2}{N}_{main}\frac{R_{main}}{R_i}{\left(R_i-r_i\right)}^2\cdot \left(\frac{1}{R_{main}}+\frac{1}{R_{mandrel}}+\frac{1}{R_i}-\frac{1}{r_i}\right) \]$

(13)

$\[ V_{\text{max}}=\frac{2{\left(\text{arctan}\mu \right)}^2{N}_{main}{R}_{main}^2}{R_i\left(1+R_{main}/R_{mandrel}\right)}\cdot \left(\frac{1}{R_{main}}+\frac{1}{R_{mandrel}}+\frac{1}{R_i}-\frac{1}{r_i}\right) \]$

(14)

3. 적합성형조건 검증을 위한 유한요소해석

3.1 유한요소해석 조건

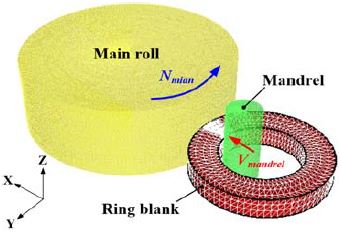
적합성형조건을 이용하여 설계된 단일과정 수평식 링 압연공정의 유효성을 검증하기 위하여 Figure 4에 나타난 것처럼 유한요소모델을 구성하여 성형해석을 수행하였다. 해석에 사용된 소프트웨어는 Forge 2009이며, 센터링 롤 옵션을 사용해 링의 중심 위치를 자동으로 유지시켜 공정 안정성을 확보하였다.

Figure 4:

Shape defects in ring rolling process

링 압연공정의 해석은 사각 단면의 평면 링에 대하여 수행되었다. 링 블랭크의 재료는 AISI 1035이며, 탄성계수와 프아송 비는 각각 200 GPa 및 0.3이다. 다양한 온도 및 변형률 속도에서 고온 압축시험이 수행되었으며 응력-변형률 선도를 Figure 5에 나타내었다. 재료의 비열, 열전도도 및 방사율은 각각 778Jkg^-1°C^-1, 35.5Wm^-1°C^-1 및 0.88 이다. 링과 구동 롤의 접촉면에서 마찰계수는 0.178 이고 맨드렐의 접촉면에서 마찰계수는 0 이다[9]. 모든 롤은 강체로 가정되었고 각 롤의 치수, 초기 링 블랭크 및 제품 치수 등의 일반적인 조건들은 Table 1에 나타내었다.

Figure 5:

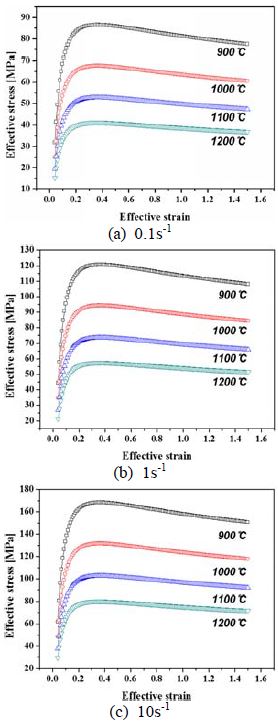
Effective stress-strain curves of AISI 1035 carbon steel alloy under different temperature and strain rates

Table 1:

Input parameters required for PRRR process verification

링의 두께를 감소시키는 맨드렐의 이송속도의 최소 및 최대 값은 적합성형조건에 의해 각각 1.194 mm/s와 2.03 mm/s로 계산된다. 유한요소해석은 아래 5가지 경우로 구분되어 수행되었다.

(i) Case 1: V_mandrel,1=0.363 mm/s, 임의의 최소 이송속도
(ii) Case 2: V_mandrel,2=0.780 mm/s, Lin과 Zhi에 의해 제안된 최소 이송속도 [7]
(iii) Case 3: V_mandrel,3=1.197 mm/s, 최소 이송속도(V_min)
(iv) Case 4: V_mandrel,4=1.613 mm/s, 임의의 중간 이송속도
(v) Case 5: V_mandrel,5=2.030 mm/s, 최대 이송속도(V_max)

3.2 유한요소해석 결과

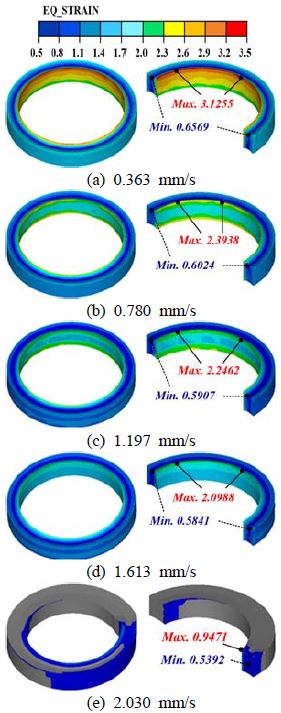
링 압연공정의 유한요소해석을 통해 맨드렐 이송속도가 링 형상, 온도 및 유효변형률 분포에 미치는 영향을 분석하였다. Figure 6은 압연된 링 제품의 형상을 맨드렐의 이송속도에 따라 나타낸 것이다. Figure 6 (a) - Figure 6 (d)의 결과로부터 이송속도가 0.363 mm/s부터 1.613 mm/s인 경우 링 압연공정이 안정적으로 잘 수행되었음을 알 수 있다. 하지만 Figure 6 (e)에 나타나듯이 최대 이송속도인 2.030 mm/s에서 압연된 링은 불균일한 두께를 가지며, 과도한 어미 결함으로 인해 외경 확장이 충분히 이루어지지 않았다. 따라서 단일과정 수평식 링 압연공정이 성공적으로 수행되기 위해서는 맨드렐은 최대 속도 이하에서 이송되어야 한다.

Figure 6:

Shape of deformed rings under different Vmandrel in PRRR process

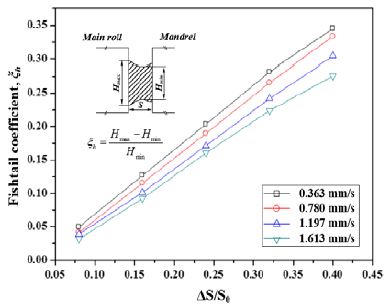
일반적인 압연공정에서는 압하량이 증가할수록 재료의 퍼짐량은 증가한다. 평면 링 압연 시, 최소 및 최대 퍼짐은 각각 링 두께방향의 중간 영역 및 롤과의 접촉 영역에서 나타난다. 맨드렐의 다양한 이송속도에 따라 링 압연공정이 진행될 때, 두께 감소에 따른 높이방향으로의 상대적인 퍼짐량을 정량화하기 위해 어미 계수(Fishtail coefficient, ζ_h)를 활용하였다. 맨드렐 이송속도가 2.030 mm/s인 경우는 목표한 링 외경에 도달하지 못하였기 때문에 퍼짐에 대한 고찰에서는 제외되었다.

$\[ {\zeta }_h=\left(H_{\text{max}}-H_{\text{min}}\right)/H_{\text{min}} \]$

(15)

Figure 7에 나타나듯이 맨드렐 이송속도가 증가할수록 어미 계수는 현저하게 감소되었다. 구동 롤의 1회전 당 맨드렐의 압하량이 상대적으로 증가하면 소성변형영역은 롤과의 접촉면뿐만 아니라 링 두께방향으로도 충분히 침투하게 된다. 이러한 침투조건은 링 표면 영역의 퍼짐량 및 어미결함을 감소시킨다. 적합성형조건의 최소 이송속도인 1.197 mm/s 이상에서 어미 결함은 상대적으로 감소되었다.

Figure 7:

Fishtail coefficient with different feed rates of mandrel in PRRR process

맨드렐 이송속도가 링의 유효변형률 분포에 미치는 영향을 Figure 8에 나타내었다. 유효변형률은 링 중심에 비하여 표면에서 상대적으로 높게 나타났으며, 맨드렐과 접촉되는 링 내면에서 가장 높은 변형률이 관찰되었다. 이송속도가 느릴수록 최대 유효변형률 및 링 내·외면의 변형률이 상대적으로 증가하여 불균일한 변형 거동이 심화되었다.

Figure 8:

Effective strain distribution of deformed ring in PRRR process

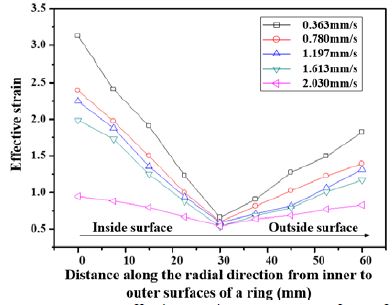
Figure 9는 단일과정 수평식 링 압연공정에서 다양한 맨드렐 이송속도에 따라 변형된 링 상부표면의 평균 유효변형률 값을 나타낸 것이다. 맨드렐 이송속도가 증가할수록 링 내·외면의 유효변형률 및 전반적인 변형의 불균일성이 감소되었다. 이송속도의 증가에 따라 재료의 침투조건이 개선되어 재료 유동은 원활히 이루어졌다.

Figure 9:

Average effective strain on upper surface of deformed ring in PRRR process

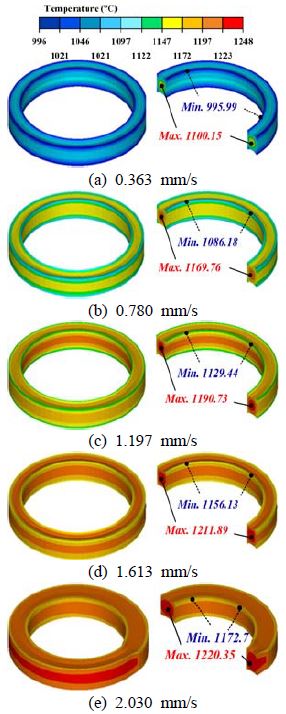
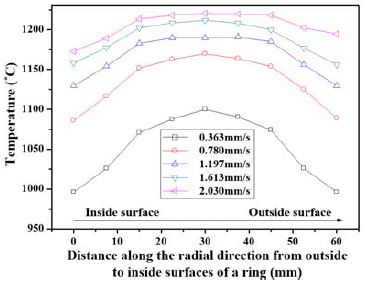
Figure 10은 단일과정 수평식 링 압연공정에서 변형된 링의 온도 분포를 나타낸 것이다. 맨드렐 이송속도가 증가할수록 최소․최대 온도 값이 증가하였으며 링 내․외부의 온도 편차가 현저히 감소하였다. Figure 11에 나타난 것처럼 맨드렐 이송속도의 증가로 인해 재료 열 손실이 감소되고 동시에 더 많은 소성변형 열이 발생하기 때문에 온도 분포는 상대적으로 균일해졌다.

Figure 10:

Temperature distribution of deformed ring in PRRR process

Figure 11:

Average temperature on upper surface of deformed ring in PRRR process

4. 결 론

본 연구에서는 링 압연공정의 어미 결함을 최소화하는 공정을 설계하기 위하여 단일과정 링 압연공정의 적합성형조건을 개발하였다. 연구의 결과를 요약하면 다음과 같다.

• (1) 링 외경증가속도를 기준으로 한 링 압연공정의 제어 알고리즘을 제시하였다.
• (2) 압연 가능한 최소마찰계수를 고려한 평면 변형-압입공정의 슬립라인 이론 및 힘의 평형방정식을 이용하여 단일과정 수평식 링 압연공정에서 맨드렐 최소 및 최대 이송속도를 제안하였다. 결함을 최소화할 수 있는 적합성형조건은 식 (12)에 나타내었다.
• (3) 대형 링의 열간 유한요소해석 결과, 제안된 적합성형조건 하에서 성형 시 링 제품의 어미 결함은 상대적으로 감소되었으며 유효변형률 및 온도 분포가 균일해졌다. 편차가 상대적으로 감소되었다.

Acknowledgments

본 연구는 2017년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구결과이며(No. 2017R1C1B5017016), 이경훈의 박사학위논문(“An Innovative Process Design of Plain and Profile Ring Rolling for Improving Shape Accuracy, 부산대학교 대학원”)을 개선한 것이다.

References

• S. L. Semiatin, ASM handbook, vol. 14A. Metal working: bulk forming, Ohio, ASM International, (2005).
• J. T. Yeom, J. H. Kim, D. G. Lee, N. K. Park, S. S. Choi, and C. S. Lee, “Process design for large-scale ring rolling of Ti-6AL-4V alloy”, Transaction of Material Processing, vol. 16(no. 3), p172-177, (2007), (in Korean).
• A. Kluge, Y. H. Lee, H. Wiegels, and R. Kopp, “Control of strain and temperature distribution in the ring rolling process”, Journal of Materials Processing Technology, vol. 45(no. 1-4), p137-141, (1994). [https://doi.org/10.1016/0924-0136(94)90331-x]
• J. B. Hawkyard, W. Johnson, J. Kirkland, and E. Appleton, “Analyses for roll force and torque in ring rolling, with some supporting experiments”, International Journal of Mechanical Sciences, vol. 15(no. 11), p873-893, (1973). [https://doi.org/10.1016/0020-7403(73)90018-0]
• R. Hill, The mathematical theory of plasticity, Oxford, Clarendon Press, (1950).
• A. G. Mamalis, J. B. Hawkyard, and W. Johnson, “Spread and flow patterns in ring rolling”, International Journal of Mechanical Sciences, vol. 18(no. 1), p11-16, (1976). [https://doi.org/10.1016/0020-7403(76)90069-2]
• H. Lin, and Z. Z. Zhi, “The extremum parameters in ring rolling”, Journal of Materials Processing Technology, vol. 69(no. 1-3), p273-276, (1997). [https://doi.org/10.1016/s0924-0136(97)00029-0]
• L. Guo, and H. Yang, “Towards a steady forming condition for radial-axial ring rolling”, International Journal of Mechanical Sciences, vol. 53(no. 4), p286-299, (2011). [https://doi.org/10.1016/j.ijmecsci.2011.01.010]
• K. H. Lee, and B. Y. Kim, “Advanced feasible forming condition for reducing ring spreads in radial-axial ring rolling”, International Journal of Mechanical Sciences, vol. 76, p21-32, (2013). [https://doi.org/10.1016/j.ijmecsci.2013.08.007]