173,000 CBM 액화천연가스 운반선의 선체변형을 고려한 추진축계 정렬해석 연구
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
선체변형이 축계 베어링 손상사고의 한 가지 원인으로 밝혀지면서 선주 및 선급에서는 선체변형을 고려한 보다 강화된 축계정렬해석을 요구하고 있다. 또한 관련 기준 및 규정 또한 강화되고 있다. 이러한 업계와 선주 및 선급의 요구에 부응하기 위하여, 본 연구에서는 173,000 CBM 액화천연가스의 흘수 변화에 따른 전선구조해석을 유한요소법을 이용하여 실시하고 전선구조해석으로부터 얻어진 축계의 상대변위를 이용하여 축계정렬해석을 수행하였다. 전선구조해석은 선박의 흘수 변화를 고려한 3가지 조건에서 수행하였다. 이를 바탕으로 선체변형에 따른 베어링 하중 변화가 축계정렬해석에 미치는 영향을 검토 하였다. 선체변형을 고려한 경우에서도 축계지지베어링 하중은 허용 하중 이내에 있는 것을 확인하였다.
Abstract
As the hull deflections have been identified as one of the causes for shafting bearing damage, a more strengthened shafting alignment analysis which is considered with hull deflections, is required by the Owner and Class. Moreover, the trend for the related criteria with rules has been strengthened. To meet the needs of the industry with the Owner and the Class, global structural analysis using the finite element method was performed for a 173,000CBM liquefied natural gas carrier according to the ship’s draft changes in this study. The shafting alignment was performed depending on the relative displacement of the shafting obtained by the global structural analysis carried out for three conditions considering the ship’s draft changes. Based on this, the effect of bearing load changes on the shafting alignment was reviewed due to the hull deflections. Even if the hull deflections are considered, all shafting bearing loads were observed to be within the permissible bearing load.
Keywords:
Shaft alignment, Shafting alignment analysis, Global structural analysis, Relative displacement, Finite element method키워드:
축계정렬, 축계정렬해석, 전선구조해석, 상대변위, 유한요소법1. 서 론
추진축계 배치에 관한 연구는 1950년대 후반 미국 해군 함정에서 중요성이 대두된 이후 개개의 베어링에 대한 최적의 위치를 결정하는 이론이 정립되기 시작하였다. 이 성과는 점차 일반 선박으로 확대되었으며, 1960년대 후반부터 1970년대 초반에 걸쳐 활발한 연구가 전개되어 많은 부분에서 관련 이론들이 확립되게 되었다[1]-[4].
또한, 조선기술 및 철강기술의 발전과 함께 선박은 고출력화, 대형화됨에 따라 추진축의 강성은 증가한 반면 선체는 고장력 후판의 적용으로 이전의 선체보다 훨씬 더 쉽게 변형되는 단점이었다[5]. 이는 기존의 선박보다 더욱 정교한 축계정렬이 요구됨을 의미한다.
이에 따라, 본 연구에서는 대형 액화천연가스 운반선을 대상으로 선박의 흘수 변화에 따른 전선구조해석을 실시하고 전선구조해석으로부터 얻어진 축계의 상대변위를 이용하여 축계정렬해석을 수행하였다. 구조해석은 선박의 흘수 변화를 고려한 3가지 조건에서 수행하였다. 또한, 선체변형을 고려한 것과 고려하지 않는 축계정렬을 비교하였고, 이를 바탕으로 선체변형에 따른 베어링 하중 변화가 축계정렬에 미치는 영향을 검토하였다.
2. 축계정렬기준
2.1 선미관 베어링
선미관 후부 베어링은 어떠한 경우에도 베어링의 투영 면적 기준으로 면압은 0.8 MPa를 초과해서는 안 된다. 선미관 전부 베어링은 축계 구동 조건에서 1.2 MPa까지 허용하고 있으며, 베어링 하중은 어떠한 경우에도 양(+)의 값이 적용되어야 한다. 음(-)의 값을 가지는 하중이 작용하는 결과는 해당 베어링의 윗면에 축이 닿았다는 것을 의미하기 때문에 허용될 수 없다. 만일 선미관 전부 베어링에 하중이 거의 작용하지 않거나 해석결과가 0.1 MPa 이하가 되는 경우에는 횡진동 해석을 통하여 축계에서 횡진동 영향이 없는지를 확인해야 한다[6].
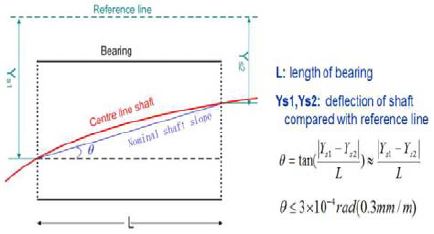
선미관 후부 베어링 내면과 프로펠러 축의 상대 경사도가 정적인 조건에서 0.3 mm/m를 초과해서는 안 된다. 축계정렬해석 결과에서 이를 초과하는 경우에는 선미관 후부 베어링의 내부에 경사를 적용하여 상대 기울기가 0.3 mm/m 이내가 되도록 대부분의 선급협회에서 조정하도록 규제하고 있다. Figure 1은 선미관 후부 베어링 경사도에 대한 기준이다.
Criterion of single bearing slope [7]
2.2 중간축 베어링
중간축 설치 시 유의점은 중간축 베어링의 종방향 위치와 수직방향 위치(옵셋)에 관한 것들이 있다. 중간축 베어링과 인접한 베어링간의 거리가 짧을수록 해당 중간축의 영향계수가 커지게 되므로[7] 인접 베어링에 불필요한 부하를 가지게 하며, 반면에 인접 베어링간의 거리가 길수록 축계의 유연성은 증가하나 횡진동을 야기할 수 있다[8].
중간축 베어링 허용면압 기준은 일반적으로 베어링 제작사의 권장치를 따른다. 베어링 제작사의 권장치가 없는 경우에는 정적인 조건에 0.8 MPa을 초과해서는 안 되며, 동적인 조건에서는 1.2 MPa까지 허용하고 있다. 베어링 하중은 어떠한 경우에도 양(+)의 값으로 작용해야 한다. 만일 중간축 베어링에 하중이 거의 작용하지 않거나 해석된 결과가 0.5 MPa 이하로 되는 경우는 횡진동 해석을 통해서 축계에 횡진동 영향이 없는지를 확인해야 한다[6].
2.3 주기관 베어링
주기관 베어링의 허용하중은 엔진 제작사의 권고치에 따른다. Table 1은 본 연구에서 적용한 주기관 베어링의 허용하중이다.
Acceptable bearing load for by MAN B&W
2.4 추진축계 배치시 고려사항
문헌[8]에 의한 허용치는 통상 프로펠러 축은 15 ~ 25 MPa, 중간축은 10 ~ 25MPa, 추력축은 20MPa이며, 축의 재질에 따라 허용 굽힘 응력이 결정되지만, 축계의 굽힘 응력을 과도하게 제한하는 것은 축계배치에 있어서 바람직하지 않을 수도 있다. 유연한 축계 배치 일수록 큰 굽힘응력이 발생하므로 횡진동(whirling vibration) 및 피로강도를 만족하는 범위 내에서 어느 정도의 높은 굽힘응력 상태는 성공적인 축계 배치의 반증으로 볼 수 있다.
축계 배치에 있어서 운전시에 발생하게 되는 다음과 같은 사항을 고려해야 할 것이다[9].
- (1) 흘수나 항로의 변경에 따른 2중저(double bottom)의 변형
- (2) 정지상태와 운전상태간의 온도차로 인한 디젤기관, 또는 터빈과 감속기어의 팽창
- (3) 정지상태의 축이 운전하면서 선미관 베어링 유효지점이 이동하는 것
- (4) 프로펠러의 추력중심과 축계의 중심위치가 어긋남의로써 발생하는 추력에 의한 굽힘 모멘트
- (5) 베어링 마멸(특히 해수윤활 lignum vitae의 경우)
- (6) 축이나 프로펠러의 회전에 의한 불평형 관성력
- (7) 가능한 한 선미관 후부 베어링에서 하중의 분포가 균일할 것. 즉 선미단에 베어링 하중이 국부적으로 편중되지 않을 것
감속기어를 갖는 터빈이나 디젤기관에서는 감속 기어장치가 비교적 짧기 때문에 축계 중심선의 평균 기울기가 베어링 중심선에 평행하게 되도록 축계 지지대나 베어링 및 감속 기어장치를 여기에 맞도록 낮추어서 배치할 수 있다. 그러나 저속 디젤기관은 상응하는 기울기를 갖도록 설치하기에는 너무 길기 때문에 선미관 베어링에 상응하는 기울기를 갖도록 보링(boring)하거나 베어링 부시(bush)의 외경을 상응하는 기울기가 되도록 가공한다. 후자의 방법이 정확한 기계가공이 가능하기 때문에 바람직한 방법이다.
3. 선체변형을 고려한 축계정렬 해석방법
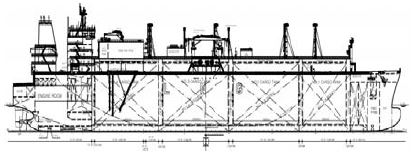
Table 2는 본 연구에 이용한 선박의 주요치수이며, Figure 2는 일반배치도를 나타내었다.
Principle dimension of the ship
General arrangement of the ship
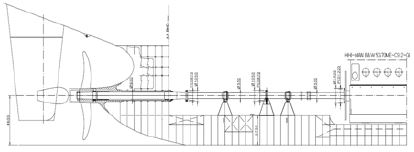
Table 3은 축계의 주요사양이며, MAN B&W사의 ME-GI 엔진을 설치하였다. Figure 3은 축계 배치도이며, Figure 3에서 나타난 바와 같이 중간축 베어링이 2개 적용되었다.
Specifications of Shafting System
Propulsion Shafting Arrangement
3.1 전선구조해석
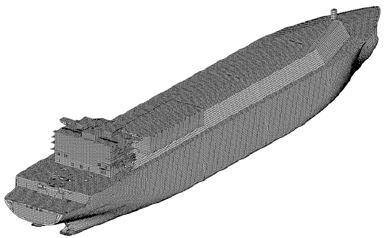
선체변형을 해석하기 위해서 전후처리 프로그램으로 MSC/PATRAN을 사용하였고, solver로 MSC/NASTRAN을 사용하였다. 일반적인 강도해석에서 사용되는 전선구조해석과는 몇 가지 다른 점이 있다. 강도해석에서는 선미구조를 약간 굵게 모델링하는 반면 본 축계정렬해석을 위한 선체변형해석에서는 상세하게 모델링하게 된다. 이는 선미 측 선체변형의 단위 변화를 좀 더 자세히 보기 위함이다. Figure 4은 전선구조해석을 위한 모델링이며, Figure 5은 선미관 부분의 구조해석이며 보다 정확히 구현하기 위해서 그림에서 보여준 봐와 같이 좀 더 세밀한 격자(mesh : 100 x 100)로 모델링 하였으며, 그 이외 부위의 격자(mesh : 820 x 820)는 종 부재 간격으로 모델링 하였다. 해석에서 사용된 좌표계는 다음과 같다. 즉, AP에 원점을 설정하였고, 기선상(base line)을 따라서 x축을 설정하였는데 전방을 양의 방향으로 설정했다. 수직상향을 양의 z축으로 설정하였고, 좌현 쪽을 양의 y축으로 설정하였다.
Full ship FE model overall view
Aftbody and engine room area at a shaft center line
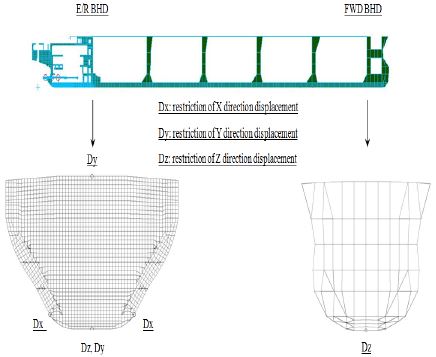
3.2 경계조건
전선구조해석에 적용된 경계조건은 Figure 6에 나타내었다. 기선상과 E/R BHD(bulkhead)가 만나는 점, 그리고 FWD BHD과 기선상이 만나는 두 점에 수직방향(z방향)의 병진변위(DZ)를 구속하였다. 이중저 탱크 상부, E/R BHD 및 외부 외판 및 E/R BHD가 만나는 점 그리고 상갑판, E/R BHD 및 중심선이 만나는 점에 횡방향(y방향) 변진 변위(DY)를 구속하였다.
Boundary condtion
3.3 하중조건
하중조건은 Table 4와 같이 3가지 조건에 대해여 검토 하였다. 하중조건 St1은 안벽 흘수이며, 이 조건에서 최종 정렬작업이 수행된다. St2는 발라스트 흘수이며 이 조건에서 선체는 최대 호깅(hogging) 상태로 변형된다. St3은 만재 흘수 조건이며, St3은 실제 운항조건으로 최대 새깅(sagging) 상태로 변형이 된다.
Loading conditions
3.4 해석결과
Figure 7은 안벽흘수에서의 전체 변형 패턴을 보여주는데, 그림에서 보여주는 봐와 같이 안벽 흘수 에서는 선체가 호깅 상태로 변형된다는 것을 알 수 있다. Figure 8은 발라스트 흘수에서의 전체 변형 패턴을 보여주고 있으며, 선체가 새깅으로 변형이 된다는 것을 알 수 있다.
Hull deformation at quay
Hull deformation at ballast
앞서 전선구조해석으로 얻어진 변위를 절대변위라 했고, 실제 이 변위를 사용하여 직접 정렬해석을 수행해도 아무런 영향을 미치지 않는다. 위에서 보여준 절대변위는 경계조건이 적용된 두 점을 연결하는 직선을 기준선(reference line)으로 하여 측정된 변위를 나타낸다. 일반적으로 조선소에서는 선미관 후부 베어링의 중심과 선미관 전부 베어링의 중심을 연결하는 직선을 정렬작업의 기준선으로 설정한다. Figure 9은 전선구조해석에서 나온 해석결과를 나타낸 것이며, Table 5는 전선구조해석에서 나온 해석결과를 테이블로 나타냈다.
Relative shaft deflection with respect to the reference line
Relative shaft deflection with respect to the reference line
4. 축계정렬해석
축계정렬해석을 수행을 위해서 Figure 10과 같이 DNV Nauticus 축계정렬해석 프로그램을 사용하여 모델링하여 축계정렬해석을 수행하였다.
Modelling for shafting alignment
베어링 강성은 제작사 권고치를 주로 반영하며, 본 연구에서는 다음과 같이 적용하였다. 선미관 베어링은 6.0 x 109 N/m, 중간축 베어링은 2.0 x 109 N/m, 주기관 베어링은 5.0 x 109 N/m을 적용하였다.
Table 6은 베어링 및 주기관 제작사가 권고하는 베어링 허용 하중[10][11]을 나타낸 것이며, 축계정렬해석 수행 시 베어링 허용 하중이 초과하지 않도록 각별히 유의해야 한다.
Permissible bearing load
축계정렬해석을 위해서 적용되는 기본 물성치는 Table 7과 같이 적용하였고, 외력은 제작사에 권고에 따라 Table 8과 같이 적용하여 축계정렬해석을 수행하였다.
Shaft material data
External load
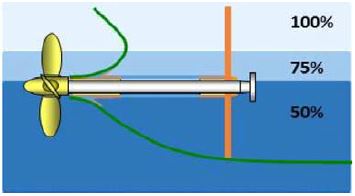
축계 정렬 설치 조건에 따라 프로펠러가 해수에 부분적으로 잠기는 것을 고려하여 해석을 수행한다. 일반적으로 프로펠러의 잠수량 표시는 Figure 11과 같다. 본 연구에서는 진수 후 선박에 흘수 조건에 따라서 안벽은 50%를 적용하였고, 발라스트 및 만재 흘수은 프로펠러가 완전히 잠기는 조건(100%)으로 축계 정렬을 수행하였다.
Propeller submerged condition [6]
5. 해석 결과 및 고찰
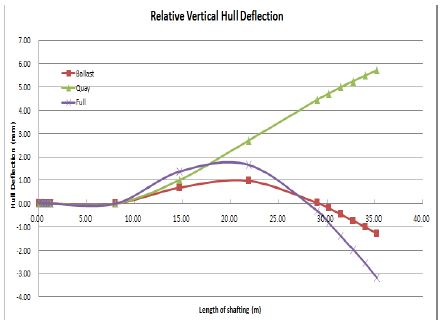
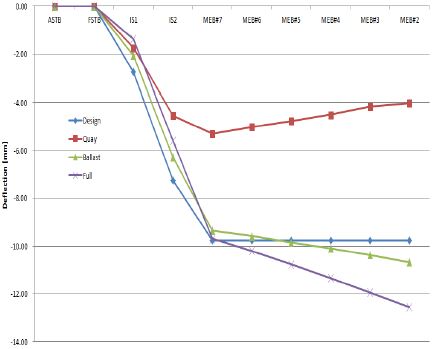
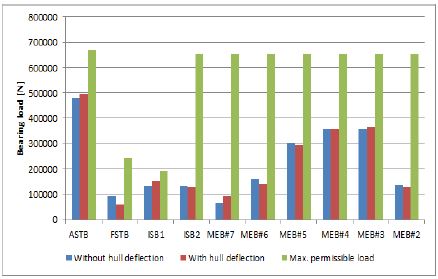
Table 9는 Table 5에서 나온 선체변형을 베어링 옵셋을 적용하고 설계치를 비교하여 나타낸 것이며, Figure 12은 Table 9를 이용하여 그래프로 나타내었다.
Bearing offsets by the effect of hull deflection
Draught dependent relative shaft deflection curves
Table 9에서 나타난 것처럼 안벽 흘수 조건에서는 선체변형이 설계치보다 감소하는 것으로 나타났으나, 그 원인으로써는 안벽흘수에서는 프로펠러의 잠수량이 50% 정도이며, 호깅 현상으로 선체가 축 중심보다 상향하는 것을 알수 있다. 또한, 흘수 변화에 따른 프로펠러 및 선체 부력에 인한 원인으로 추정 된다. 선체변형은 만재 흘수로 갈수로 설계치보다 베어링 옵셋이 증가하는 것으로 나타났다. 이러한 현상은 흘수 변화 및 운항조건 변경으로 선체가 물에 더 많이 잠겨서 발생되는 원인이다.
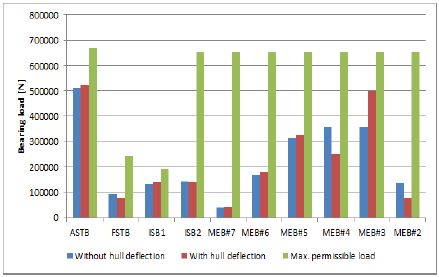
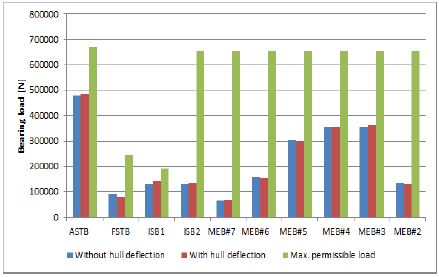
Figure 13 ~ Figure 15는 Table 9에서 나온 선체변형을 반영하여 축계정렬해석을 수행 후 베어링 반력값을 설계치와 비교한 결과를 나타내었다. 그 결과 축계지지베어링은 Table 6에서 제시된 허용치 이내로써 적적하게 부하를 분담하고 있음을 알 수 있다.
Bearing loads at quay
Bearing loads at ballast
Bearing loads at full
Figure 13과 같이 안변 조건의 주기관 베어링 (MEB4)의 반력은 선체변형을 고려하지 않을 때와 141%의 편차를 보이고 있으며, 주기간 베어링(MEB4) 베어링의 반력은 72%의 편차를 보여주고 있다. 그러나 그 값은 제작사 권고한 허용치 대비 각각 48%, 77% 이하로서 크랭크축 베어링에 부적정인 영향을 미치지 않을 것으로 판단한다.
Figure 14와 같이 발라스트 조건에서는 모든 베어링에 편차가 없는 것으로 나타났지만, Figure 15와 같이 만재흘수 조건의 선미관전부베어링(FSTB) 반력은 선체변형을 고려했을 시 차이가 있으나 제작사에서 권고한 허용치를 만족하므로 부정적인 영향을 미치지 않을 것으로 판단된다.
6. 결 론
본 연구에서는 173,000 CBM 액화천연가스 운반선의 선체변형을 고려한 축계정렬해석 연구를 수행하였다. 또한 전선해석을 통해 얻어진 안벽, 발라스트, 만재흘수에서의 선체변형량을 축계정렬해석에 반영하여 축계 안정성 여부를 검토하였다.
본 연구의 주요 결과를 요약하면 다음과 같다.
- (1) 전선구조해석 결과, 발라스트 흘수에서 만재 흘수로 이동할수록 축계는 선체변형 영향으로 설계치 대비 베어링 옵셋은 증가하는 반면에, 안벽 흘수에서는 베어링 옵셋이 설계치 대비 감소하는 것으로 예측되었으며, 그 원인으로써는 안벽흘수에서는 프로펠러 잠수량이 50% 정도이며, 호깅 현상으로 인하여 선체가 축 중심보다 상향하는 것을 발견하였다. 이것은 흘수 변화에 따른 프로펠러 및 선체 부력에 인한 원인으로 추정 된다. 선체변형은 만재 흘수로 갈수로 설계치보다 베어링 옵셋이 증가하는 것으로 나타났다. 이러한 현상은 흘수 변화 및 운항조건 변경으로 선체가 물에 더 많이 잠겨서 발생되는 원인으로 예측된다.
- (2) 안변 조건의 주기관 베어링 (MEB4)의 반력은 선체변형을 고려하지 않을 때와 141%의 편차를 보이고 있으며, 주기간 베어링(MEB4) 베어링의 반력은 72%의 편차를 보여주고 있다. 그러나 그 값은 제작사 권고한 허용치 대비 각각 48%, 77% 이하로서 크랭크축 베어링에 부적정인 영향을 미치지 않을 것으로 판단되며, 만재조건에서도 선미관전부베어링의 반력이 차이가 있었으나 제작사 기준치에 모두 만족하는 것으로 판단된다.
- (3) 따라서, 선체변형을 고려한 경우에서도 축계지지베어링의 하중은 고려된 모든 조건 하에서도 허용 하중 이내에 있는 것을 확인하였으며, 이를 통해 본 연구 대상 선박인 경우 축계 유연성을 가지고 있는 것으로 판단되었다.
- (4) 본 연구를 통해 예측된 선체 변형량은 향후 유사선박의 축계정렬 검토 시 참고가 될 것으로 사료된다.
- (5) 본 연구를 통해 예측된 선체 변화량을 고려한 축계 정렬을 실선 계측을 통해 추후 비교를 통해 선체 변화량을 고려한 축계정렬에 정확성을 확인해 볼 필요가 있다고 판단된다.
References
- M. Rudolph, “A quarter century of propulsion shafting design practice and operating experience in the U.S. navy”, The Journal of the American Society of Naval Engineers Journal (NEJ), vol.71(no.1), p153-164, (1959).
- H. C. Anderson, and J. J. Zrodowski, “Co-ordinated alignment of line shaft, propulsion gear, and turbines”, Annual Meeting of Society of Naval Architects and Marine Engineers(SNAME), vol. 67, p449-523, (1959).
- W. E. Lehr, and E. L. Parker, “Considerations in the design of marine propulsion shaft system”, Society of Naval Architects and Marine Engineers (SNAME), vol. 67, p555-601, (1961).
- Graeme Mann, “Shipyard alignment of propulsion shafting using fair curve alignment theory”, The American Society of Naval Engineers Journal, vol. 77(no. 4), p651-659, (1965).
-
J. U. Lee, “A study on the analysis of bearing reaction forces and hull deflections affecting shaft alignment using strain gauges for a 50,000 DWT oil/chemical tanker”, Journal of the Korean Society for Marine Engineering, vol. 40(no. 4), p288-294, (2016), (n Korean).
[https://doi.org/10.5916/jkosme.2016.40.4.288]
- J. S. Sun, A Study on Shaft Alignment of Propulsion Shafting System Depending on Reaction Supporting Position and Slope of Aft Stern Tube Bearing, Ph.D. Dissertation, Department of Mechanical Engineering, Korea Maritime and Ocean University, Korea, (2017), (in Korean).
- Class NK, GUIDELINES ON SHAFTING ALIGNMENT, Japan, Class NK, (2006).
- H. J. Jeon, Ship Propulsion Transmission Equipment, Busna, Korea, Taehwa Publishing Company, (1986), (in Korean).
-
J. U. Lee, “A case study on the optimal shafting alignment concerning bearing stiffness for 10,100 TEU container carrier”, Journal of the Korean Society of Marine Engineering, vol. 40(no. 3), p185-190, (2016), (in Korean).
[https://doi.org/10.5916/jkosme.2016.40.3.185]
- MAN B&W, Bearing Load Measurement by Jacking Up, ID No. 07424-5, (2011).
- KR, Rules for the Classification of Steel Ships Part 5 Chapter 3 206, Busan, Korea, Korean Register, (2015).