캔틸레버형 헬리데크에 대한 비선형 좌굴 안전성 평가

1. 서 론

헬리데크(Helideck)는 해양플랜트로 운용인원 및 물자를 수송하는데 필수적인 시스템이며 비상 시 탈출수단으로 사용되어 그 중요성이 크다[1]. 때문에 영국 정부 산하 산업안전기구(Health and Safety Commission)에서는 해양구조물에 탑재되는 헬리데크의 안전 및 설계에 대한 종합적 기술보고서를 출간하였으며[2], 이에 따르면 ICAO, API, CAA 및 DNV 등 여러 주요기관에서 헬리데크 구조설계 가이드라인을 제시하고 있다. 특히 이들 간의 공통적인 고려사항은 헬리콥터의 착륙조건과 착륙하중 그리고 풍하중이며, 이에 대해 여러 선행연구들이 수행된 바 있다.

먼저 착륙하중에 대해서, Fasanella 등은 헬리데크로의 헬리콥터 착륙 충돌 연구를 수행하였다[3]. 비선형 양해법(Nonlinear explicit method) 기반의 시간이력 동적 해석 코드를 적용한 유한요소 모델로 헬리콥터를 구현하여 착륙 충돌 시뮬레이션 프로그램을 개발하였다. 그 결과 시간에 따른 헬리콥터의 착륙 및 충돌 시나리오를 시간 영역에서 예측하였으며, 충돌로 인해 헬리콥터 구조부재에 작용하는 충격력을 산정하였다. 또한 이러한 결과들을 실험 데이터와 비교하여 그 정확성을 검증하였다. 한편 Veghefi 등은 헬리콥터의 비상착륙에 의한 연직 및 수평하중 하에서 비선형 정적해석기법(Pushover analysis)을 이용해 헬리데크의 응답을 해석하였다[4]. 먼저 헬리데크 위로 9개 착륙위치를 정한 후, 헬리콥터 최대 이착륙 연직하중 및 수평하중을 4개의 바퀴면적을 통해 데크에 충격하중으로 작용시키고, 이를 상용프로그램 SACS를 통해 해석하였다. 그 결과를 이용해 케이스 별 Von-Mises 곡선을 생성하여 비선형성을 보이는 하중 계수의 크기를 구해냄으로써 극한강도(Ultimate strength)를 산출했다. 더불어 Pushover 곡선을 생성하여 구조의 붕괴단계(Collapse step)에서의 하중 계수를 찾아냈다. 결과적으로, 비상착륙조건에서 헬리콥터의 축 회전이 부재들의 구조적 강도를 낮추는데 유의한 영향을 미쳤음을 확인하였다. Chen 등은 중국 북해(Beihai sea) 내 해양구조물의 헬리데크 모델을 대상으로 한 풍동 실험을 통해, 풍향에 따른 풍속분포의 차이를 관찰하였다[5]. 또한 모서리 앞에서의 유동박리(Flow separation) 현상, 헬리데크 중심부에서의 불안정한 평균 풍속, 데크 중심과 상부 모서리 사이에서의 큰 풍속 변화 등 헬리데크의 부위별 형상에 따라 작용하는 풍하중 특성을 규명하였다.

한편 헬리데크 설계에 관해서, Park 등은 헬리데크 설계 변수에 대한 다양한 케이스 스터디를 수행하였다[6]. 상부의 플레이트(Plate), 보강재(Stiffener) 및 하부의 거더(Girder), 트러스(Truss) 등으로 구성된 헬리데크를 유한요소 모델로 구현하고, 데크 자중, 부속장비의 무게, 선박의 관성력과 헬리콥터 비상착륙하중을 고려하여 구조해석을 수행하였다. 특히 비상착륙하중 산정을 위해, 여러 규정에서 정한 바와 같이 착륙 충격에 의한 동적 하중을 준정적 관점에서 산정한 계산법을 이용하였다. 구조해석에서 각 구조 부재별 설계 변수를 달리하여 다양한 케이스 스터디를 수행함으로써 허용응력 기준에서 설계 변수들의 최적값을 도출하였다. 이를 통해 여러 비상착륙 조건에서의 헬리데크 부재들이 보이는 구조적 특성을 파악하였고, 설계변수를 개선함으로써 안전성을 확보하는 동시에 강재를 절감할 수 있음을 보였다.

한편 비용절감 및 무게에 민감한 종류의 해양구조물에 적용하는 것을 목적으로 경량화된 헬리데크를 개발하기위한 연구 또한 여러 방면에서 수행되어 왔다[7]-[10]. 가장 최근 연구로, Jung 등은 헬리콥터 착륙 시 상부 플랜트 시설과의 충돌을 방지할 수 있으며 추가적인 공간 확보에 용이한 캔틸레버형 헬리데크(Cantilever-type helideck)의 경량화를 위해 위상최적설계(Topology design optimization) 기법을 적용하여 하부 트러스 구조의 배치를 결정하고 가장 큰 응력이 발생한 케이스를 기준으로 허용응력을 넘지 않도록 부재단면 치수를 조절하여 허용응력 기준에 부합하는 설계를 제시하였다[11]. 그러나 헬리데크를 구성하는 여러 부재들은 단면에 비해 길이가 긴 세장형 구조이므로 좌굴 등 동적 안전성(Dynamic stability)에 대한 검토가 필요하다.

이에 본 연구에서는 Jung 등에 의해 제시된 헬리데크 모델을 대상으로 상용구조해석 프로그램 ANSYS Mechanical APDL을 이용해 착륙하중과 풍하중이 조합된 45개 하중 케이스에 대한 선형 좌굴해석을 수행함으로써 착륙하중에 대한 선형 좌굴하중을 도출하고, 그중 가장 낮은 좌굴하중을 가진 케이스의 1차 좌굴 모드형상을 초기결함(Initial imperfection)으로 적용하여 비선형 정적해석(Nonlinear static analysis)을 통해 비선형 좌굴에 대한 안전성을 검증하고자 한다.

2. 헬리데크 구성 및 해석조건

2.1 헬리데크의 구성

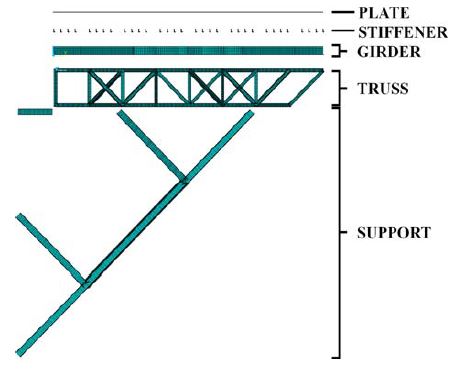
본 연구에서 참고한 헬리데크 모델은 Figure 1과 같은 형태로 보강재가 부착된 플레이트, 거더, 트러스 및 서포트 부재로 구성되어 있고, 재질은 선박이나 해양구조물에 널리 쓰이는 HT-32로 선정하였다. 그 영률(Young’s modulus)은 200GPa, 푸아송 비(Poisson ratio)는 0.3, 항복응력(Yield stress)은 315MPa로 알려져 있다.

Figure 1:

Structural members of the helideck [11]

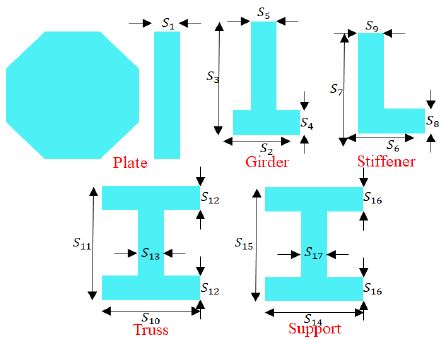
Figure 2 에서는 각 부재의 형상을 나타내는데, 플레이트는 팔각형, 거더는 뒤집힌 T형 단면, 보강재는 L형 단면, 트러스와 서포트는 H형 단면의 빔이다. 각 부재단면치수의 경우, 플레이트 두께(S₁)는 0.014m, 거더 단면의 폭(S₂), 높이(S₃), 플랜지(Flange) 두께(S₄), 웹(Web) 두께(S₅)는 각각 0.250m, 0.750m, 0.024m, 0.010m, 보강재 단면의 폭(S₆), 높이(S₇), 플랜지 두께(S₈), 웹 두께(S₉)는 각각 0.100m, 0.300m, 0.026m, 0.022m, 트러스 단면의 폭(S₁₀), 높이(S₁₁), 플랜지 두께(S₁₂), 웹 두께(S₁₃)는 각각 0.300m, 0.300m, 0.018m, 0.016m, 서포트 단면의 폭(S₁₄), 높이(S₁₅), 플랜지 두께(S₁₆), 웹 두께(S₁₇)는 각각 0.600m, 0.600m, 0.036m, 0.032m이다.

Figure 2:

Cross-section of each member

2.2 해석조건

헬리데크 설계에는 헬리콥터의 착륙하중과 다양한 환경하중들이 고려되어야 한다. 특히 본 연구에서는 구조적 좌굴과 관련하여 좁은 착륙바퀴 면적에 국부적으로 큰 하중이 작용하는 착륙하중을 우선적으로 고려하였다. 헬리콥터의 착륙조건은 일반착륙조건(Normal landing condition)과 비상착륙조건(Emergency landing condition)으로 구분된다. 일반착륙조건이란 헬리콥터가 바퀴 3개로 헬리데크 중앙에 안전하게 착륙하는 조건이며, 비상착륙조건은 조종 미숙, 엔진 문제, 장애물과의 충돌, 해상 날씨 등으로 헬리콥터가 헬리데크 중앙에 안전하게 착륙하지 못하는 조건이다. 일반적으로 비상착륙조건에서 더 큰 착륙 하중이 발생하기 때문에 본 연구에서는 비상착륙조건에 대한 동적 안정성 검토를 수행하였다. 특히 비상착륙상황 중에서도 가장 큰 착륙하중이 발생하는 조건을 고려하기 위해 헬리데크 플레이트의 가장자리에 바퀴 한 개로 착륙하는 상황을 가정하였다.

착륙하중의 크기는 착륙조건에 따른 계수들을 헬리콥터 최대 이착륙 중량(Maximum Take-Off Weight; MTOW)에 곱하는 방식으로 계산하며, 해당 계수들은 규정별로 조금씩 차이를 보인다. 기본적으로, 헬리콥터 이착륙 충격에 기인한 동적하중을 준정적 하중으로 계산하기 위한 동적 하중계수(Dynamic load factor)가 적용되고, CAA [12]와 ICAO [13]의 경우 추가적으로 착륙 플랫폼(Landing platform)의 구조 응답계수(Structural response factor)를 고려한다. 본 연구에서는 가장 보수적인 DNV의 동적 하중계수과 CAA의 구조 응답계수를 모두 적용하여 착륙하중을 식 (1)과 같이 계산하였다.

$\[ P_v=1.3\times C_d\times g\times MTOW \left(kN\right) \]$

(1)

여기서, C_d는 동적 하중계수로 비상착륙조건에서 3을 적용하였고[14], g는 중력가속도(9.81m/s²)이며 MTOW로는 현재 해상에서 운용되는 헬리콥터 중 가장 무거운 EH-101의 최대 이착륙중량인 14.6톤을 적용하였다[11]. 또한 계산된 착륙하중을 헬리데크 플레이트에 압력으로 가하기 위해 더블 휠 타입인 해당 기종 바퀴면적을 가로 400mm, 세로 200mm인 직사각형으로 환산하여 착륙하중의 작용면 형상을 모델링하였다[14].

한편 DNV-OS-E401[14]에 따르면 헬리데크 설계 시 고려해야할 환경하중으로 풍하중(Wind force), 적설하중(Snow loads), 갑판 침입수하중(Green sea loads)이 있으며, 헬리콥터가 착륙하는 상황에서는 풍하중만을 고려하도록 제시하고 있다. 앞서 언급한 바와 같이 본 연구에서는 착륙하중을 필수적으로 고려해야 하기 때문에, 적설하중과 갑판 침입수하중은 배제하고 해석하였다. 이 외에, 일반적으로 해양구조물을 설계할 때 고려해야 할 대표적 환경조건으로 조류와 파랑이 있으나, 수선면 위에 위치하는 헬리데크에는 조류와 파랑에 의한 직접적인 유체력(Hydrodynamic force)이 작용하지 않는다. 또한 본 논문에서는 헬리데크가 탑재되는 구조물을 고정식으로 가정하여 모선의 관성력에 대한 파랑하중(Wave force)은 고려되지 않았다.

DNV에서는 동적하중인 풍하중을 헬리데크의 판에 연직하방으로 작용하는 정적 압력으로 간주하며, 그 크기는 아래의 식 (2)와 같다.

$\[ P_w=\frac{1}{2}{C}_p\rho V^2 \]$

(2)

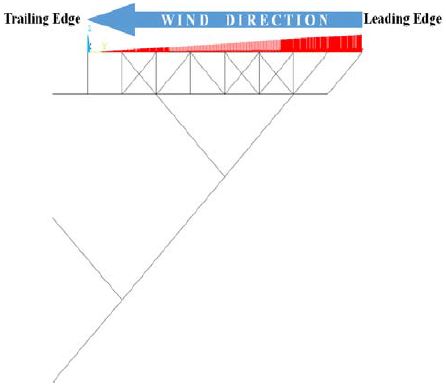
여기서, ρ는 공기의 밀도 1.225kg/m³, C_p는 압력계수(Pressure coefficient)이며, V는 평균 수위의 10m 위에서 1분간 발생하는 풍속의 평균값이다. DNV에서는 헬리콥터의 착륙 조건(Landing condition)일 경우 30m/s를 적용한다. 또한 C_p는 Figure 3과 같이 리딩 엣지(Leading edge)에서 2.0을 트레일링 엣지(Trailing edge)에서 0을 적용하여 풍하중을 삼각분포압력의 형태로 계산한다[14].

Figure 3:

Wind force on the helideck plate

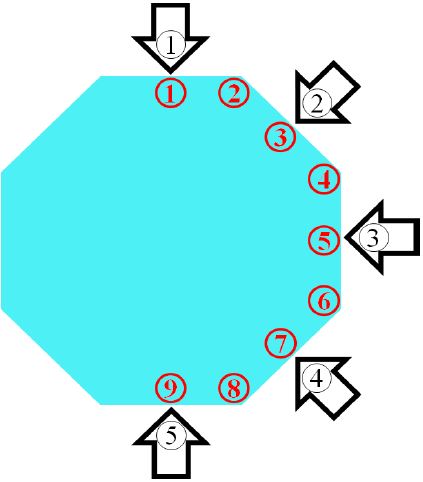
앞서 언급한 바와 같이 풍하중을 삼각분포압력으로 간주하기 때문에 풍향에 따라 하중의 분포가 달라진다. 착륙하중 역시 가장자리 착륙위치에 따라 다른 결과가 나올 수 있다. 따라서 헬리데크 설계 시 다양한 착륙위치와 풍향의 조합들을 모두 검토해야 하며, 그 중 최악의 조합에 대해서도 안전성을 확보해야 한다. 이에 본 논문에서는 헬리데크 형상의 대칭성을 고려하여, Figure 4와 같이 가장자리 9개의 착륙위치와 5개의 풍향으로 조합된 45개의 하중케이스에 대한 선형 좌굴해석을 통해 좌굴에 가장 취약한 하중조건을 찾고 그에 대한 비선형 해석을 추가적으로 수행한다.

Figure 4:

Landing locations and wind directions

3. 해석방법

3.1 선형좌굴해석

45개 하중 케이스 중 좌굴에 가장 치명적인 케이스를 찾기 위해 고유치(Eigenvalue) 기반 선형좌굴해석(Linear buckling analysis)으로 임계 좌굴하중(Critical buckling load)을 계산한다. 각각의 하중 케이스에서 자중, 풍하중, 착륙하중이 동시에 작용하지만, 자중은 변하지 않으므로 임계좌굴하중으로 고려될 수 없다. 또 국부적으로 큰 하중이 가해지는 착륙하중이 풍하중보다 구조 부재의 좌굴에 더 큰 영향을 준다고 볼 수 있다. 따라서 본 연구에서는 각 케이스별 1차 고유모드에 대해 자중과 설계 풍하중 하에서 선형좌굴이 발생할 때의 착륙하중을 도출하여 이를 임계 좌굴하중으로 계산한다.

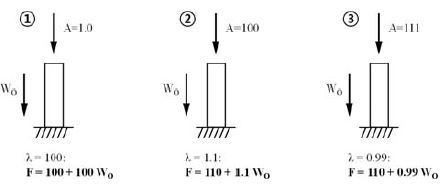
한편, ANSYS MAPDL에서는 선형좌굴해석 결과로 해당 좌굴모드에서의 좌굴하중계수(Buckling load factor)를 산출한다[15]. 이 파라미터는 해당 모드에서 임계좌굴하중에 도달하기 위해 주어진 모든 하중에 동일하게 곱해지는 비례 요소(Scale factor)로 볼 수 있다. 즉 단일 하중 조건 하에서는 좌굴하중계수를 주어진 하중에 곱함으로써 임계좌굴하중을 바로 계산할 수 있으나, 본 연구와 같이 자중, 풍하중, 착륙하중의 복합하중이 작용하는 조건에서는 정확한 좌굴하중계수를 얻기 위해 추가적인 절차가 필요하다. 예로 Figure 5의 1과 같이 자중과 외력이 함께 작용하는 경우에 계산된 좌굴하중계수가 100이라면 임계좌굴하중의 크기는 자중과 외력의 합에 100을 곱한 값이 된다. 다시 말하면, 항상 일정한 자중에까지도 좌굴하중계수가 곱해지기 때문에 변수인 외력에 대해 정확한 임계좌굴하중을 구할 수 없게 된다. 이 문제를 해결하기 위해서는 Figure 5의 2, 3과 같이 좌굴하중계수가 1.0에 매우 근사한 값이 될 때까지 외력의 크기를 조절해가며 반복계산을 수행하여야 한다.

Figure 5:

Buckling load factor and critical buckling load [15]

따라서 본 논문에서는 일정한 자중과 설계풍하중 조건 하에 착륙하중을 증감시키며 오차범위 0.01 내에서 좌굴하중계수가 1.0에 도달하도록 반복계산을 수행함으로써 착륙하중에 대한 임계좌굴하중을 찾았다.

3.2 비선형해석

비대칭성, 초기응력 등 구조의 불완전성으로 인해 선형좌굴이론에 따른 임계 좌굴하중보다 낮은 하중에서 좌굴이 발생할 수 있다. 따라서 비선형성을 고려한 좌굴하중을 추가적으로 산정하여 설계를 검토해야 할 필요성이 있다.

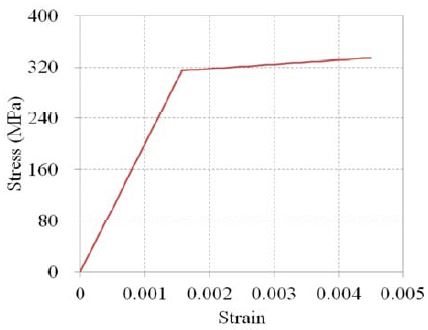
본 연구에서는 재료비선형(Material nonlinearity)을 고려하기 위해 Figure 6처럼 항복응력 이전에는 200GPa 의 영률을, 이후에는 그것의 1/30을 접선탄성계수(Tangential modulus)로 가지는 이선형 응력-변형률 곡선(Bi-linear stress- strain curve)을 적용하였다[16]. 이와 함께 기하비선형(Geometric nonlinearity)을 고려하기 위해 모델에 초기결함을 가하고 대변형(Large deformation) 응답을 포함한 해석을 수행하였다. 부연하면 45개 하중 케이스 중 선형 좌굴해석 결과 가장 위험한 케이스에서의 1차 좌굴 모드 형상(Buckling mode shape)을 초기결함으로 주었으며, 부재 길이의 0.0015배를 초기결함의 최대치로 적용하였다[14]. 비선형해석은 뉴턴-랩슨 반복법 기반의 선탐색기법(Line search method)을 사용하였으며, 반복횟수(Substep)는 20으로 설정하였다. 강재의 경우 일반적으로 소성 변형률(Plastic strain)이 0.2%에 도달하였을 때를 항복으로 간주한다[16]. 따라서 본 논문에서는 이 항복상태를 비선형 좌굴로 보고 해당 상태에 도달할 때의 착륙하중을 비선형 좌굴하중이라 판단하였다.

Figure 6:

Bi-linear stress-strain curve

4. 결과 및 토의

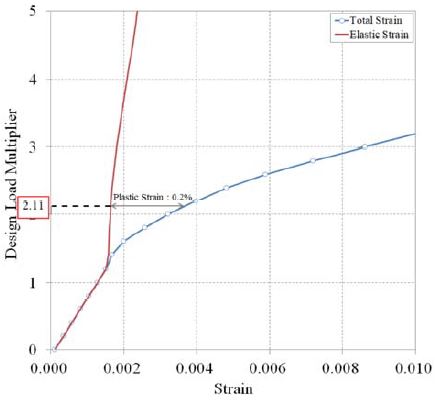
선형 좌굴해석을 통하여 45개의 하중 조건에 대해 얻어진 각각의 임계 좌굴하중을 설계 착륙하중에 대한 비(μ_cr)로 표현한 결과는 Table 1과 같다. 우선 45개의 모든 하중 조건에서 μ_cr이 1보다 큰 값을 가지므로 선형 좌굴에 대해서 안정성을 확보했다고 판단할 수 있다. 다만 이 중에서 착륙위치 2번, 풍향 1번 조합에서 μ_cr이 2.6818로 가장 작기 때문에 좌굴에 대해서 가장 위험할 수 있는 조건이라 볼 수 있다. 따라서 이 조건에 대해서 추가적으로 비선형 좌굴해석을 수행하였으며 그 결과는 Figure 7과 같다.

Table 1:

μcr for linear buckling analysis under 45 load cases

Figure 7:

Design load multiplier(μ)-strain curve

Figure 7은 μ에 따른 변형률의 변화를 총 변형률(Total strain)과 탄성 변형률(Elastic strain)로 구분하여 나타내고 있다. 여기서 총 변형률 곡선과 탄성 변형률 곡선의 차이가 소성 변형률이다. 약 1.2 이하의 μ에서는 총 변형률 곡선과 탄성 변형률 곡선이 μ에 선형 비례하는 형태로 일치함을 알 수 있다. 즉, 소성 변형이 발생하지 않는 선형 탄성구간임을 의미한다. 반면에 이보다 큰 μ에서는 총 변형률 곡선과 탄성 변형률 곡선 간에 격차가 벌어지며, 이는 소성 변형이 발생함을 의미한다. 또한 μ가 증가함에 따라 두 곡선 사이의 거리가 멀어져 소성 변형률도 점점 커짐을 알 수 있고, μ가 약 2.11일 때 소성 변형률이 0.2%에 도달한다. 따라서 이를 항복점으로 판단하고 μ_cr=2.11로 계산할 수 있다. 이는 앞서 살펴본 선형 임계좌굴하중인 2.6818의 약 78.9%로, 실제 좌굴은 임계 좌굴하중보다 약 21% 낮은 착륙하중에서 발생함을 알 수 있다. 하지만 좌굴에 가장 취약한 하중조건에서도 설계 착륙하중에 대해 좌굴이 발생하지 않으며, 그보다 약 2.11배 큰 착륙하중이 헬리데크에 가해질 때 비로소 좌굴이 발생하게 됨을 알 수 있다.

5. 결 론

본 논문에서는 선행연구를 통해 허용응력 기준으로 설계된 헬리데크에 대해서 추가적인 좌굴 안전성을 검토하였다. 특히 자중, 풍하중, 착륙하중의 복합하중을 받는 헬리데크에 대해서, 좌굴의 주요 원인인 착륙하중에 대한 선형 및 비선형 좌굴해석을 수행하였다. 그 결과 선형 좌굴해석에 의한 임계 좌굴하중은 설계 착륙하중의 약 2.68배, 비선형 해석에 의한 비선형 좌굴하중은 설계 착륙하중의 약 2.11배로 나타나, 주어진 헬리데크 모델은 비상착륙조건에서도 좌굴에 대한 구조적 안전성이 확보되었음을 확인하였다.

Acknowledgments

이 논문은 2015년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업이며(No. NRF-2015R1C1A1A01051797), 정태원의 석사학위논문(“위상 최적설계를 활용한 캔틸레버식 헬리데크 구조 설계 및 해석, 한국해양대학교 대학원”)의 일부를 포함하고 있다.

References

• Y. J. Park, Optimization of Deck-mounting Type Helideck Using F.E. Analysis, M.S. Thesis, Department of Naval Architecture and Ocean Engineering, Busan National University, Busan, (2014), (in Korean).
• Graham Morrison, Helicopter Safety Offshore, Offshore Technology Report 2000/89, Health and Safety Executive (HSE), UK, (2001).
• E. L. Fasanella, R. L. Boitnott, K. H. Lyle, and K. E. Jackson, “Full-scale crash test and simulation of a composite helicopter”, International Journal of Crashworthiness, vol. 6(no. 4), p485-498, (2010). [https://doi.org/10.1533/cras.2001.0192]
• M. Vaghefi, H. Bagheri, and S. R. Mohebpour, “Nonlinear analysis of offshore helidecks due to the helicopter emergency landing loads”, Middle-East Journal of Scientific Research, vol. 13(no. 10), p1351-1358, (2013).
• Q. Chen, Z. Gu, T. Sun, and S. Song, “Wind environment over the helideck of an offshore platform”, Journal of Wind Engineering and Industrial Aerodynamics, vol. 54(no. 55), p621-631, (2000).
• D. H. Park, Y. J. Park, J. S. Park, and J. H. Kim, “Parametric study for helideck design using finite element analysis”, Journal of Ocean Engineering and Technology, vol. 28(no. 55), p411-422, (2014), (in Korean). [https://doi.org/10.5574/ksoe.2014.28.5.411]
• O. G. Hizir, Structural Weight Optimization of a Naval Ship Helideck, M.S. Thesis, Department of Naval Architecture and Marine Engineering, Istanbul Teknik University, Turkey, (2010).
• J. H. Choi, “Structural integrity evaluation method for offshore aluminum helidecks”, Journal of the Korean Society of Mechanical Engineers, vol. 56(no. 1), p46-50, (2016), (in Korean).
• J. S. Jo, J. H. Choi, and J. H. Kim, “The structural performance study of aluminum helideck for offshore”, Proceedings of KSME 2015 Annual Meeting, p1306-1309, (2015), (in Korean).
• J. B. Koo, J. S. Park, Y.S. Ha, K.B. Jang, and Y. S. Suh, “Nonlinear structural response analysis for aluminum helideck”, Proceedings of the 24th International Society of Offshore and Polar Engineers (ISOPE) Conference, p15-20, (2014).
• T. W. Jung, B. M. Kim, and S. H. Ha, “A study on lightweight design of cantilever-type helideck using topology design optimization”, Journal of Computational Structural Engineering Institute of Korea, vol. 30(no. 5), p453-460, (2017), (in Korean). [https://doi.org/10.7734/coseik.2017.30.5.453]
• Standards for Offshore Helicopter Landing Areas, CAP-437, Civil Aviation Authority (CAA), (2013).
• Heliport Manual, Doc 9261-AN/903, International Civil Aviation Organization (ICAO), (1995).
• Helicopter Decks, OS-E401, Det Norske Veritas (DNV), 2001.
• SAS IP, Inc., Procedure for Eigenvalue Buckling Analysis, https://www.sharcnet.ca/Software/Ansys/17.2/en-us/help/ans_str/Hlp_G_STR7_5.html Accessed January 15, 2017.
• S. R. Satish Kumar, and A. R. Santha Kumar, “1.3 Mechanical properties of steel”, Design of Steel Structures, vol. 1, 1st ed., Madras, Department of Civil Engineering, Indian Institute of Technology Madras, p13-18, (2010), [Online]. Available: http://priodeep.weebly.com/uploads/6/5/4/9/65495087/design_of_steel_structures_bookzz.org_[iit_madras]_.pdf.
• T. W. Jung, Structural Design and Analysis of Cantilever-type Helideck using Topology Design Optimization, M.S Thesis, Department of Ocean Engineering, Korea Maritime and Ocean University, Busan, (2018), (in Korean).