Peak frequency shift 기법을 이용한 단일채널 해양탄성파 탐사자료의 Q-factor 산출 연구

1. 서 론

최근 인류의 활동영역이 육상에서 점차 해양으로 이동함에 따라 대규모 교량, 항만, 방파제 건설과 같은 해양 건설 공사부터 파이프라인, 해저 케이블, 해양 플랜트와 같은 구조물의 설치와 골재채취 등의 해양 자원 개발 사업까지 해양에서의 다양한 사업이 수행되어지고 있다. 이러한 이유로 해양토목시공을 위하여 지반조사 및 안전성 확보를 목적으로 하는 엔지니어링 규모의 탐사 수요가 증가하고 있다[1]. 국내의 엔지니어링 규모의 탄성파 탐사는 수심 및 해양환경 조건에 따른 제약으로 인해 단일채널 탄성파 탐사가 주로 수행되고 있다[2].

엔지니어링 목적의 소규모 해양 탄성파 탐사는 장비가 열악할 뿐 아니라, 자료처리를 위한 기술이 매우 부족한 실정이다. 반면에 자원개발 목적의 탄성파 탐사는 탐사규모가 대규모이고 단일채널 수진기가 아닌 다중채널 수진기를 이용하여 탐사를 주로 수행하며, 고급 자료처리 기술까지 적용을 하여 다양한 분석들을 실시한다.

단일채널 탄성파 탐사는 기동성이 좋으며 자료취득이 간편하고 적은 비용으로 탐사를 수행할 수 있어 엔지니어링 목적의 탐사에서 많이 사용되고 있지만, 탐사자료로부터 직접적으로 확인가능한 정보가 많지 않아 지층의 경계, 기반암 확인 정도에 그치는 경우가 대부분이다[3]. 하지만 엔지니어링 목적의 탄성파 탐사의 산업이 지속적으로 성장하면서 그 중요성이 증가되고, 이에 따라 단일채널 탄성파 탐사 자료에 대한 자료처리와 탄성파 속성 분석을 통해 정량적이고 정밀한 지하매질의 물성정보 취득 필요성 및 퇴적물 분류에 관한 연구가 부각되고 있다. 퇴적물 분류 등 지층의 물성정보를 확인하기 위한 Q-factor는, 트레이스의 진폭 분석, 해상도 향상뿐만 아니라 암석학, 유체의 포화도 및 투과율에 관한 연구에도 활용된다[4]. 탄성파 감쇠를 정량적으로 나타내는 Q-factor는 가스 하이드레이트의 부존여부 및 매장량에 관한 정보를 제공해주는 매우 중요한 요소이다[5].

따라서, 본 연구에서는 탄성파 감쇠를 표현하는 Q-factor를 산출하고자 수치모형실험으로 취득된 자료로부터 각 지층에 대한 결과를 산출하였다. 이후 현장자료 모사를 모사하기 위해 30 %의 무작위 잡음을 추가하여 Q-factor를 산출하여 적용가능 여부를 판단한 뒤 실제 현장에서 취득된 탄성파 탐사자료에 적용하여 각 지층에 대한 Q-factor를 산출하였다.

2. 연구 이론

2.1 탄성파 감쇠

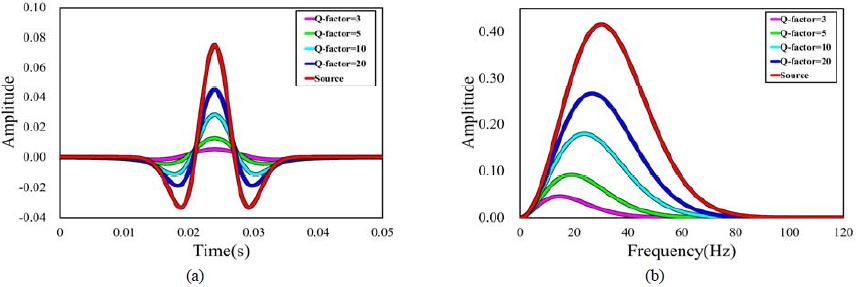
음원에서 발생한 탄성파가 지표면 방향으로 전파되고 퇴적물 내에서 전파하는 동안 탄성파의 진폭이 감소가 되는데 이때의 손실은 전파거리에 따른 기하학적 확산손실과 고유감쇠, 반사, 굴절, 회절 등에 의해 나타나는 산란으로 발생한다[6][7]. 특정 주파수 대역에서의 감쇠량을 감쇠계수로 정의할 수 있으며 이러한 감쇠계수는 탐사 조건이나 해당 매질의 특성 등 외부조건에 따라 값이 달라지기 때문에 실제로 일어나는 탄성파 감쇠만을 수치화하여 나타내기에는 어려움이 존재한다. 무차원의 변수인 Q-factor를 통해 탄성파 감쇠를 정량적으로 표현할 수 있으며, 이는 감쇠계수와 반비례 관계를 가진다[8]. 다음의 Figure 1을 살펴보면 설정된 Q-factor의 값에 따라 시간영역 및 주파수영역에서의 진폭 스펙트럼이 감쇠하는 것을 확인할 수 있다.

Figure 1:

The time domain waveform (a) and frequency spectrum (b) of a Ricker wavelet of 30Hz dominant frequency for various Q-factors (Li et al., 2015).

3. 수치모형실험 및 결과

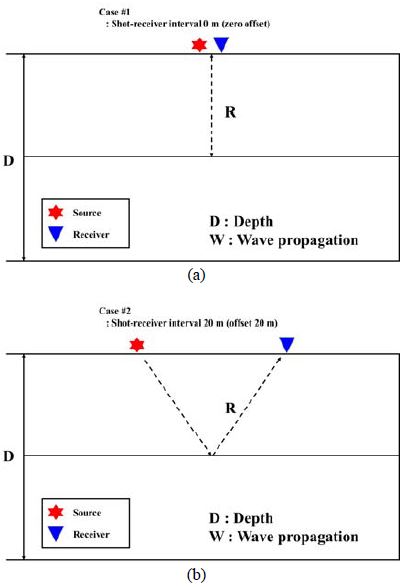
본 연구에서는 탄성파 감쇠를 표현하는 무차원 변수인 Q-factor를 산출하기 위해 peak frequency shift (PFS)를 이용하였으며, 정확도와 오차율을 분석하였다. 수치모형실험에 사용된 자료는 파선추적 알고리즘을 기반으로 한 탄성파 모델링 프로그램인 NORSAR사의 NORSAR-2D 프로그램을 사용하였다. 이는 지층의 내부를 주행하는 탄성파 전파 과정을 계산할 때, 지층의 속도 및 밀도, P파와 S파에 대한 Q-factor 값을 입력하여 수치모형으로 구현할 수 있다. Figure 2는 음원-수진기의 간격이 0 m인 제로-오프셋 탐사와 음원-수진기의 간격이 20 m인 오프셋 탐사를 통해 자료를 취득하는 모식도이며 취득된 자료에서 Q-factor를 산출하였다.

Figure 2:

A schematic diagram of single channel seismic survey: (a) offset 0 m, (b) offset 20 m

본 연구에서 사용된 수치모형실험 모델은 수평 5층 구조의 모델로 구성되어있으며, 지층 하부로 내려 갈수록 P파, 밀도, Q-factor가 증가하도록 설정하였다(Table 1).

Table 1:

A summary of physical properties of layered Earth model

Figure 2의 모식도를 토대로 수평 5층 구조에 대하여 수치모형실험을 수행하여 자료를 생성하였다. 생성된 자료에 대하여 현장자료를 모사하기 위해 30 %의 무작위 잡음을 추가하였으며 이는 각각의 층에 대한 이벤트를 육안으로 구분할 수 있을 만큼의 크기로 설정하였다(Figure 3).

Figure 3:

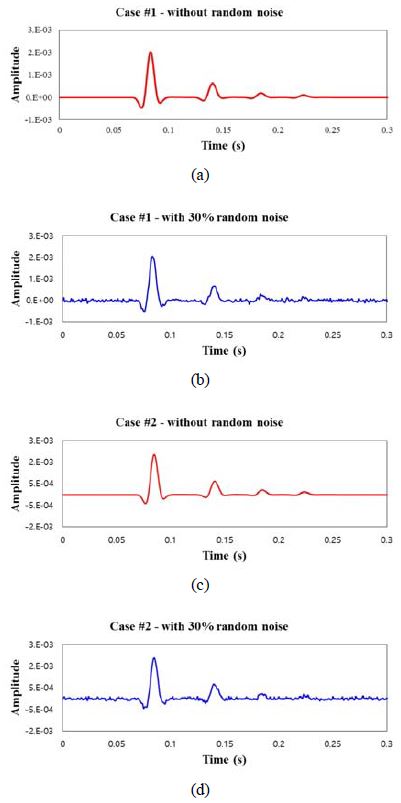
Numerical modeling results: (a) Case #1 without random noise, (b) Case #1 with 30% random noise, (c) Case #2 without random noise, and (d) Case #2 with 30% random noise.

Peak frequency shift (PFS)을 이용하여 생성된 수치모형실험에 대하여 Q-factor를 산출하였으며 무작위 잡음의 유무에 따른 결과는 아래의 표와 같이 나타내었다(Table 2; Table 3). 산출된 결과를 볼 때 무작위 잡음이 포함되지 않은 경우 설정된 Q-factor의 값과 10 % 내의 오차를 보이고 있으며, 무작위 잡음이 추가된 경우 20 % 내의 오차가 발생하는 것으로 나타났다. 이는 무작위 잡음이 추가되어 이벤트의 초동시간 선정 및 해당 주파수 성분이 변경되어 이러한 오차가 생기는 것으로 판단된다.

Table 2:

Camparison between Q-factors obtained by the PFS method from numerical model with the input for Case #1.

Table 3:

Camparison between Q-factors obtained by the PFS method from numerical model with the input for Case #2.

4. 현장자료 적용

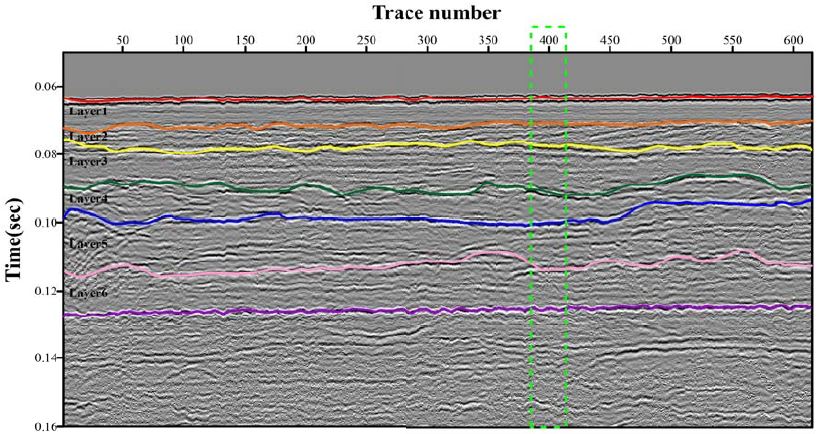
Peak frequency shift (PFS)를 이용하여 무작위 잡음이 포함된 수치모형자료로부터 Q-factor 산출 가능 여부를 확인 후 실제 단일채널 탄성파 탐사자료에 적용하여 Q-factor를 산출하였다. 본 연구에 사용된 현장자료는 경상남도 거제시 다포리에서 남동쪽으로 7 km 떨어진 해상에서 단일채널 탄성파 탐사를 통해 취득된 자료이다(Figure 4). 취득된 자료는 수직해상도를 높이기 위해 너울 필터(swell filter), 디지털 필터링(digital filtering), 디콘볼루션(deconvolution) 등의 자료처리 기법을 적용하였다[13].

Figure 4:

Seismogram obtained from Geoje (Ko et al., 2013)

자료처리를 수행한 현장자료는 Figure 4와 같으며 400번째 트레이스를 기준으로 전·후 10개의 트레이스에 대하여 Q-factor를 산출하였다(Table 4). 각 지층별로 평균 59.23, 34.16, 179.15, 11.22, 6.08의 Q-factor가 산출되었으며, 계산된 표준편차로 확인하였을 때 20 %내의 분포를 확인할 수 있다. 계산된 표준편차의 값이 클 경우 산출된 Q-factor의 분포가 넓게 나타나는 것을 확인할 수 있으며, 반대로 작을 경우 정확한 Q-factor의 값이 산출된 것으로 판단할 수 있다. 트레이스로부터 계산된 각각의 Q-factor의 값은 Figure 5와 같이 나타내었다.

Table 4:

Q-factors obtained by the PFS method from single channel seismic data in Geoje

Figure 5:

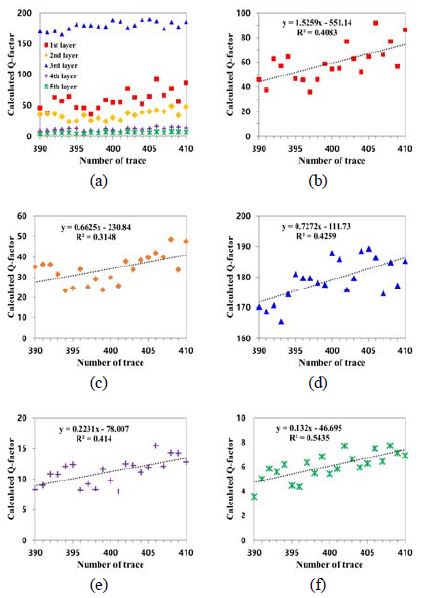
Calculated Q-factor from single channel seismic data in Geoje: (a) total, (b) 1st layer, (c) 2nd layer, (d) 3rd layer, (e) 4th layer and (f) 5th layer

결정질 암석의 경우 Q-factor의 값은 500~1000 정도로 감쇠정도가 작고, 균열이 존재하거나 다공질의 암석의 Q-factor의 값이 10~100 정도로 감쇠정도가 높은 것으로 확인된다[14]. 또한 지표나 해저면 부근의 미고결 퇴적층 및 동토층의 경우 Q-factor 값은 5~20 정도로 나타나기에 감쇠의 정도가 높은 것으로 확인된다[15]. 해수의 Q-factor는 63,000으로 매우 큰 값을 가지고 있으며, 이러한 이유로 음원에서 발생된 탄성파가 해수층을 통과하여 해저면으로 이동할 때 감쇠효과가 매우 적다[9]. E. L. Hamilton (1972)는 실내 시험분석을 통해 Q-factor에 따라 퇴적물 분류를 수행하였으며 모래의 경우 29~44, 사질 실트의 경우 23~54, 점토실트의 경우 104~368 로 확인되어진다[16].

실내 시험으로 얻어진 Q-factor의 정보와 산출된 Q-factor를볼 때 상부 층(Layer1~layer3)의 경우 미고결상태의 퇴적층으로 구성되어 있는 것으로 확인되어진다. 또한, 지층 내부의 머드나 사질 실트로 구성된 퇴적층 내 입자간의 마찰로 인한 열이 에너지로 전환되어 매질에 흡수되는 고유 감쇠와 지층을 구성하는 입자간의 공극에 따른 흡수손실 및 해수와 퇴적층 사이에서 발생하는 음향손실의 영향이 클 것으로 판단된다. 탄성파 단면도상의 4층과 5층의 경우 산출된 Q-factor를 볼 때 급격하게 감소하는 경향을 확인할수 있었으며 실내 시험으로부터 추정된 Q-factor와 비교하였을 때 모래 자갈층으로 구성되어 있는 것으로 사료된다.

산출된 Q-factor로 직접적인 퇴적물 분류를 실시하기에는 어려움이 존재한다. 이외의 탄성파 속성분석, 시추코어를 채취한 뒤 실내시험으로 얻어진 결과들과 접목시킨다면 좀 더 정확한 결과를 얻을 수 있을 것으로 판단된다.

5. 결 론

본 연구는 수치모형실험과 현장에서 취득된 단일채널 탄성파 탐사자료에 대하여 peak frequency shift (PFS)법을 적용한 뒤 Q-factor를 산출하고 퇴적물 분류를 실시하였다.

Peak frequency shift (PFS)의 적용성을 확인하기 위해 수치모형실험을 통해 생성된 자료에 대하여 무작위 잡음 추가의 유무에 따른 Q-factor를 산출하고 이에 대하여 정확도를 분석하였다. 분석결과 산출된 Q-factor값은 무작위 잡음이 없을 경우 설정된 값과의 10 %이내의 오차율을 보이고 있으며 이론값과 근사한 값을 나타내고 있다. 무작위 잡음이 추가된 경우 Q-factor를 산출하였을 때 설정된 값과 20 %이내의 오차율을 보이고 있으며, 이는 이벤트의 정확한 초동시간 선정과 무작위 잡음이 추가될 때 변경된 주파수의 성분으로 인하여 오차가 생기는 것으로 확인된다.

단일채널 탄성파 탐사를 통해 취득된 현장 자료에 대하여 Q-factor를 산출한 결과로부터 지층의 구성을 추정하였다. 상부 층(Layer1~Layer3)의 경우 미고결상태의 퇴적층으로 구성되어 있는 것으로 확인되며, 하부 층(Layer4~Layer5)의 경우 모래 자갈층으로 구성되어 있는 것으로 판단된다. 산출된 Q-factor를 볼 때 크게 감소하는 것을 볼 수 있으며, 이는 지층의 구성이 자갈, 모래 등 미고결 퇴적층으로 구성된 것으로 확인할 수 있다. 또한 고해상도의 탄성파 탐사자료를 활용 시 보다 정확한 지층의 구성을 파악할 수 있을 것으로 판단된다.

본 연구에서 사용된 peak frequency shift (PFS) 방법을 통한 Q-factor 산출과 다양한 탄성파 속성분석을 복합적으로 수행한다면 정확한 지층의 정보와 퇴적물 분류에 대한 정확성이 향상될 것으로 판단되며, 시추조사와 병행하여 얻어진 시추코어의 실내시험을 통해 Q-factor를 산출하여 비교분석을 수행하면 질 높은 자료로 사용될 수 있을 것으로 판단된다. 본 연구를 바탕으로 해양 건설공사, 해양플랜트 산업에 필요한 지반조사 및 안정성 확보에 관한 기초연구자료로 활용 될 수 있을 것이라 사료된다.

Acknowledgments

본 연구는 자원개발특성화대학사업단의 지원과 한국지질자원연구원 주요 사업인 “탐사선 운영효율 제고 및 기술고도화 연구” 과제(18-3313)의 일환으로 수행되었습니다.

References

• C. S. Kim, A Study on the Shallow Marine Site Survey using Seismic Reflection and Refraction Method, MS Thesis, Korea Maritime and Ocean University, Korea, (2007).
• H. K. Ko, J. H. Ha, W. K. Chung, and S. S. Shin, “Seismic attribute analysis and interpretation with single channel seismic data of shallow marine”, Journal of the Korean Society of Mineral and Energy Resources Engineers in Korean, vol. 51(no. 1), p55-67, (2014).
• W. S. Kim, E. S. Park, H. Y. Lee, H. D. Kim, K. P. Park, N. H. Koo, and S. O. Chung, “Detaild processing and analysis on the single-channel seismic data for site survery of Daecheon-Wonsando subsea tunnel”, Geophysics and Geophysical Exploration in Korean, vol. 13(no. 4), p336-348, (2010).
• A. B. Haase, and R. R. Stewart, “Estimating seismic attenuation (Q) by an analytical signal method”, Proceeding of the 2005 SEG/Houston annual meeting, p2617-2620, (2005). [https://doi.org/10.1190/1.2148261]
• K. H. Lee, and J. Matsusshima, “Influence of tuning effect on seismic attenuation estimation”, Proceeding of the 10th SEGJ international symposium, p1-4, (2011). [https://doi.org/10.1190/segj102011-001.40]
• M. R. John, An Introduction to Applied and Environment Geophysics, 2nd ed., Wiley Blackwell, (1997).
• L. E. Kinsler, A. R. Frey, A. B. Coppens, and J. V. Sanders, Fundamentals of Acoustics 4th Ed., John wiley and Sons, Hoboken, NJ, USA, p480, (2000).
• J. W. Lee, J. H. Ha, H. K. Ko, W. K. Chung, and S. S. Shin, “A study on characteristics of seismic attenuation by using spectral ratio method”, Journal of the Korean Society of Mineral and Energy Resources Engineers in Korean, vol. 51(no. 4), p687-695, (2014).
• M. Toksöz, D. Johnston, and A. Timur, “Attenuation of seismic waves in dry and saturated rocks: Ⅰ. Laboratory measurements”, Geophysics, vol. 44(no. 4), p681-690, (1979).
• L. Peselnick, and I. Zietiz, “Internal friction of finegrained limestones at ultrasonic frequencies”, Geophysics, vol. 62(no. 2), p1163-1167, (1959). [https://doi.org/10.1190/1.1438583]
• M. T. Galdwin, and F. D. Stacey, “Anelastic degradation of acoustic pulses in rocks”, Physics of the Earth and Planetary Interiors, vol 8, p17-22, (1974).
• F. Li, H. Zhou, N. Jiang, J. Bi, and K. Marfurt, “Q estimation from reflection seismic data for hydrocarbon detection using a modified frequency shift method”, Journal of Geophysics and Engineering, vol. 12(no. 2), p577-586, (2015). [https://doi.org/10.1088/1742-2132/12/4/577]
• C. Zhang, and T. Ulrych, “Estimation of quality factors from CMP records”, Geophysics, vol. 67, p1542-1547, (2002). [https://doi.org/10.1190/1.1512799]
• H. K. K, Seismic Attribute Analysis and Interpretation with Single Channel Seismic Data of Shallow Marine, M.S. Thesis, Korea Maritime and Ocean University, Korea, (2013).
• A. Gusmeroli, T. Murray, P. Jansson, R. Pettersson, A. Aschwanden, and A. Booth, “Vertical distribution of water within the polythermal Storglaciäen, Sweden”, Journal of Geophysical Research, vol. 115(no. F4), (2010). [https://doi.org/10.1029/2009jf001539]
• E. L. Hamilton, “Compressional-wave attenuation in marine sediments”, Geophysics, vol. 46(no. 2), p620-646, (1972).